肌肉痉挛俗称抽筋,是肌肉发生不自主强直收缩所产生的一种现象,不受主体意识支配。肌肉痉挛是中枢神经系统损伤最常见的并发症,严重影响肢体功能的恢复和日常生活自理能力[1]。产生痉挛的肌肉长时间处于紧张僵硬状态,这种症状在体育运动和康复训练中较为常见。尤其在下肢康复训练中,患者的下肢肌肉常常会因为康复训练时间过长,或因为肌肉疲劳等因素,而出现肌肉痉挛的情况,从而对患者造成二次伤害,严重的会出现骨折。识别出患者康复训练中的痉挛状态对于制定康复训练计划及保护患者不受二次伤害都有着十分重要的意义。痉挛可能发生在任何一块肌肉上,发生情况与人体当时肌肉使用情况有关。目前痉挛在国际上还未有一个统一的定义,学者普遍采用的痉挛定义为痉挛是属于运动神经元综合征的运动障碍表现之一,其特征为肌张力随肌肉牵张反射的速度增加而增高,伴随着由于牵张反射过度兴奋导致的腱反射亢进,肌肉痉挛的一个主要外在表现是肢体运动阻力增加。肌肉痉挛的定量性评估一直以来是肌肉痉挛研究中的一个重要课题。
痉挛评估已经有了多种方法,包括神经生理学评定法、生物力学评定法、药理学评定法、Ashworth量表、痉挛指数CSS评定等。本文采用基于形状的模版匹配法来识别痉挛信号,并以皮尔逊相关系数来分析表征下肢痉挛信号的相关性大小。
1 模版匹配法模板匹配是图像识别、目标跟踪等研究领域中一项非常重要的识别技术[2]。它是将已知的一段信息作为模版,与其他信息做比较,当信息与模版相似度到达预定的阀值时则可称信息与模版相匹配。此方法广泛运用在图像比较中。图像比较中,模版就是已知的小图像,其他信息就是一幅已知的大图像。若已知的大图像中要有与已知的小图像相同的图像,那么就一定可以通过算法将其找出。模版匹配算法分为3类:基于灰度值的模版匹配算法、基于边缘点的模版匹配算法和基于形状的匹配算法[3]。
1.1 波形识别中的模版匹配法模版匹配法在波形识别中早有运用。在脑电信号的识别中,可以通过模版匹配法来找出具有代表性的癫痫信号:棘波和尖波,以此来识别痉挛信号。棘波在癫痫脑电信号最为常见,它是由复数的神经元快速超同步放电产生的。棘波拥有明显的特征,出现时限约为20~70 ms,其幅值一般小于100 μV,波形是尖锐的,相对于背景极为突出。故可利用模版匹配法在脑电信号中找出棘波以此来判断癫痫的发生[4]。
在心电图波形识别中,研究者人工截取R波信号及T波信号作为模版,再对整段的心电图信号进行模版匹配计算可找出最相匹配的波形来到达波形识别的目的[5]。
除了生理电信号领域之外,基于形状的模版匹配法在其他领域问题也有应用。例如在电力资源领域,可以通过模版匹配法查出异常电能表用户。通常情况下,受于生活习惯的影响,电能表用户的每月用电量情况应该是相似的。以日为X轴,用电量为Y轴,一星期为周期制作波形图,其图像应是相似的。通过模版匹配法来比较折线图的相似程度可看出电能用户的异常用电情况。
1.2 基于形状的模版匹配法在痉挛信号波形识别中的适用性本文通过试验收集了下肢痉挛信号的表面肌电信号波形图像。通过对波形图像进行分析从而得到了下肢痉挛信号波形的一些特性。
1.2.1 高波形重复率如图 1(a)所示为痉挛波形,图 1(b)为正常波形,痉挛波形是一个波形在痉挛的持续时间内的重复出现,从生理学角度上来解释是肌肉发生不自主的强直收缩所引起的。肌肉不断的重复不完全收缩使表面肌电信号也出现大量重复。而一般人体运动的肌肉的运动复杂多变,不可能出现这样高的重复率。在实验中还让被测人员保持一个姿势肌肉持续发力,发现采集到的波形还是有极大的差异,显示人体无法刻意的保持这种特征波形,因此痉挛信号与普通运动时的肌电信号有极大的不同。可以作为识别方法的一个参考。
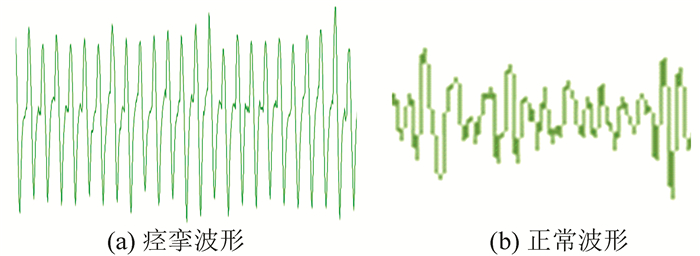
|
图 1 正常与痉挛波形 Figure 1 Normal and spasm waveform |
如图 2所示,痉挛信号中最大不重复的信号出来即基本单位波形单独研究,不难发现基本单位波形是十分简单的,波形的幅值跨度不大,波形的变化趋势也是十分简单的,在基本单位波形中波峰波谷出现的较少。从生理学的角度来解释是因为肌肉发生不完全收缩,肌肉运动不完全且较为机械,产生的表面肌电波形也较为简单。
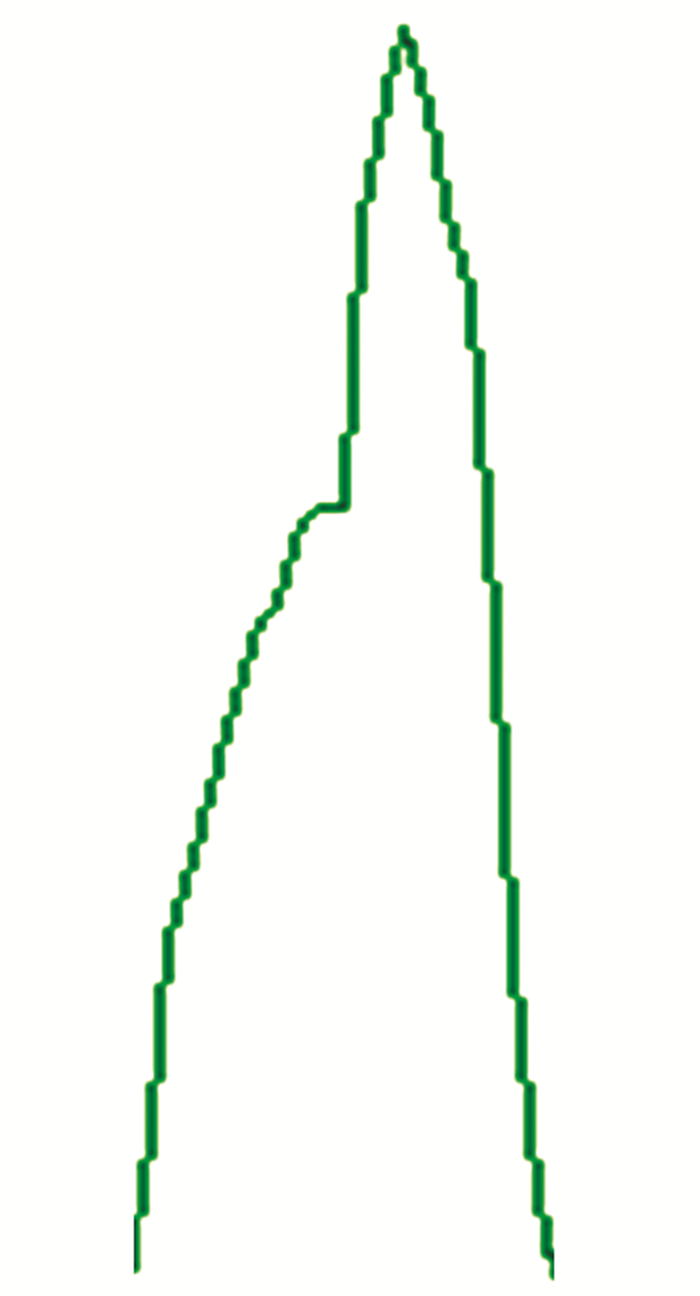
|
图 2 基本单位波形 Figure 2 The basic unit waveform |
从上述两点来看,痉挛信号的模版制作是可行的。简单的基本单位波形及极高的重复率,为模版的选取带来的极大的便利。而痉挛信号波形与一般表面肌电信号波形的巨大差异也保证了波形匹配的准确性。
2 利用皮尔逊相关系数实现模版匹配法在痉挛信号识别的运用本文在痉挛信号的识别中以基于形状的模版匹配法为核心思想,利用皮尔逊相关系数作为主要参数来实现模版匹配法在痉挛信号识别中的运用。
皮尔逊相关系数r是统计学概念,又名皮尔逊积矩相关系数(Pearson product-moment-correlation coefficient),是由卡尔·皮尔逊从弗朗西斯·高尔顿的统计思想的基础上衍化的。该系数运用于度量两个定距变量之间的线性相关性。它的值介于-1和+1之间[6],其中:
0.8 < r≤1.0,极强相关;
0.6 < r≤0.8,强相关;
0.4 < r≤0.6,中等程度相关;
0.2 < r≤0.4,弱相关;
0≤r≤0.2,极弱相关或无相关;
-1≤r < 0,负相关。
线性关系显示了当两个变量中一个变量发生变化时,另一个变量的变化情况。从波形图像上来看代表了其波形走向的相似度。从图像的整体来看表现两个变量的波形图像形状的相似度。因此皮尔逊相关系数可以作为基于形状的模版匹配法在痉挛信号识别中的主要参数,来匹配出一段被测表面肌电信号中的痉挛信号。
皮尔逊相关系数的计算公式为[7]
| $ {\mathit{r}_{xy}} = \frac{{n\sum {XY- \sum {X\sum Y } } }}{{\sqrt {\left[{N\sum {{X^2}-{{\left( {\sum X } \right)}^2}} } \right]\left[{N\sum {{Y^2}-{{\left( {\sum Y } \right)}^2}} } \right]} }}. $ |
式中:N为样本量;X、Y分别为两个变量的值;∑X为变量X值的总和;∑Y为变量Y值的总和;rxy为皮尔逊相关系数的值。
3 数据采集 3.1 仿真实验准备阶段本文目的是下肢表面肌电信号的痉挛信号的识别,因此在MATLAB仿真实验前要先收集下肢痉挛的表面肌电信号。同时由于痉挛一般出现在剧烈运动后和偏瘫病人并发症中,并且具有突发性、及时性,故采集难度较大。因此选择从上海市第一康复医院选取了相应的被测试人员:发生痉挛症状的4名男性患者,年龄42~55岁,4名女性脑卒中患者,年龄45~58岁;正常对照组,3名男性,年龄43~53岁,3名女性正常患者,年龄42~57岁。
实验采用的是芬兰Mega的ME6000表面肌电测试仪,ME6000表面体积小巧,却拥有8个通道的数据记录系统和无限遥控装置。运用了MegaMin系统来分析处理采集到正常表面肌电信号和痉挛信号,将得到的数据调出后再导入Matlab中进行运算来达到识别痉挛信号的目的。
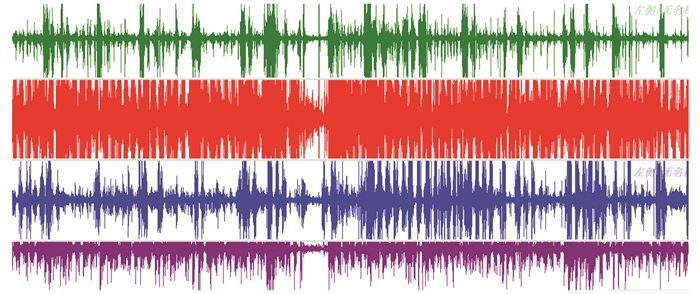
数据采集时间为151 s。总共采集了12组痉挛数据,图 3所示的为其中一次的痉挛信号图。为了与痉挛信号做对比,还采集了一般人在正常步态中的表面肌电信号。分别从腓肠肌(小腿内侧)1通道,胫骨前肌(小腿外侧)2通道,股内侧肌(大腿内侧)3通道及股外侧肌(大腿外侧)4通道。采集时间为151 s。在肌电采集过程中,运用了表面电极以避免对被测人员带来不必要的身体伤害。共获得了11组正常步态数据。图 4所示为其中一组正常信号的数据。

|
图 3 下肢痉挛信号波形 Figure 3 Lower limb spasm signal waveform |
|
图 4 正常步态信号 Figure 4 Normal gait signal |
从不同组的在下肢痉挛表面肌电信号中截取出模版信号如图 5所示,同时截取有效数据,共300个数值。将其与同组和不同组的痉挛信号分别进行仿真实验。在截取一般人正常步态的表面肌电信号将其与痉挛信号模版型号进行仿真实验。
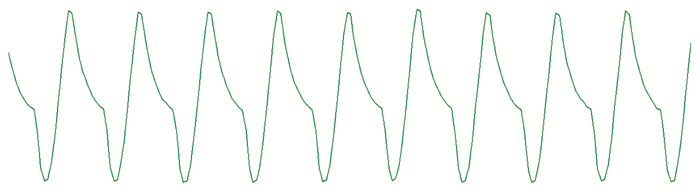
|
图 5 痉挛模版信号波形 Figure 5 Spasm template signal waveform |
将分组采集到的数据进行数据转换后,导入已经编程好的Matlab,通过运算分析得出皮尔逊相关系数r数值以及对照组的仿真图像重合度对照图。分别对数据进行了以下3组对比分析,以验证模版匹配法的准确性。
4.1 模版信号与同组痉挛信号实验将截取的模版信号与同组的痉挛信号进行MATLAB仿真实验后结果如图 6所示。
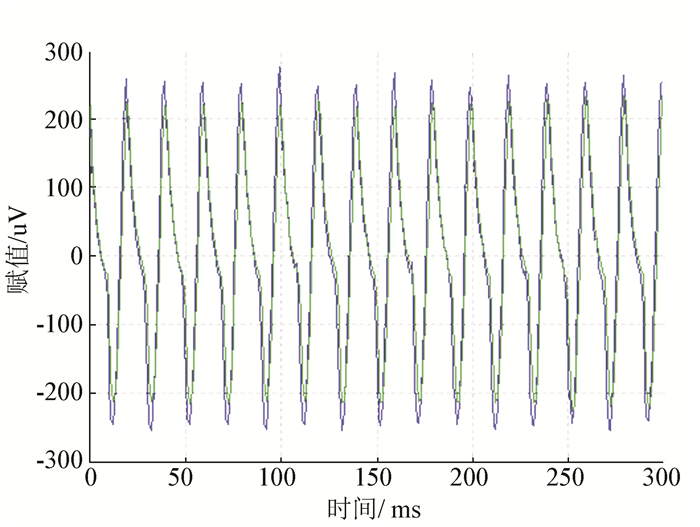
|
图 6 仿真图像与判断结果 Figure 6 The simulation image and judging results |
通过Matlab软件,计算得出皮尔逊相关系数的r数值为0.959 7,p>0.05, 显著性差异不明显,根据皮尔逊相关系数r是统计学概念,表明了模版信号与同组的痉挛信号有极高的相关度。在图 6中,2个信号的波形也基本重叠,佐证了模版信号也被测信号拥有高相关度。判断语句也显示了被测信号是痉挛信号,显示的正确的结果。证明了本文运用的算法能识别出同一人的痉挛信号。
4.2 模版信号与不同组痉挛信号实验将截取的模版信号与不同组的痉挛信号进行MATLAB仿真实验后结果如图 7所示。
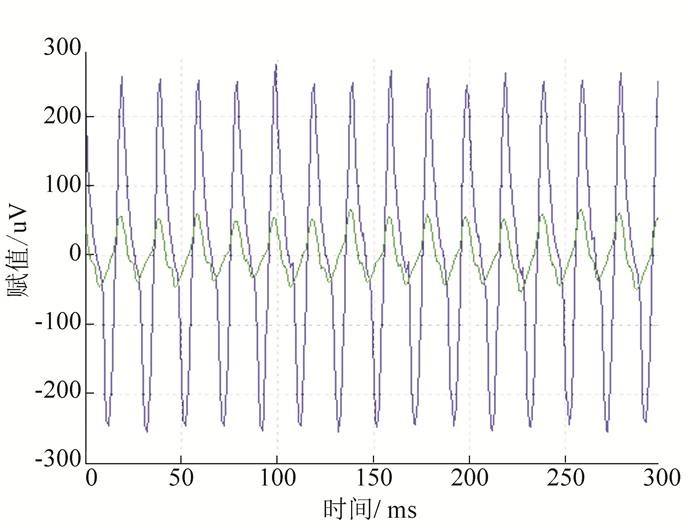
|
图 7 仿真图像与判断结果 Figure 7 The simulation image and judging results |
计算代表皮尔逊相关系数的r数值为0.643 8,p>0.05, 显著性差异不明显,根据皮尔逊相关系数r是统计学概念,表明了模版信号与不同组的痉挛信号有一定的相关度但是不足够将其认为是同一波形。在图 7中,2个信号的波形也不重叠,但是形状略有相似,佐证了模版信号与被测信号拥有一定相关度。判断语句显示了被测信号不是痉挛信号,这显然不是理想的结果。说明了本文运用的算法目前无法运用在不同人的痉挛信号识别中,但有一定的可行性。
4.3 模版信号与一般人步态实验将截取的模版信号与一般人步态实验信号进行MATLAB仿真实验后结果如图 8所示。
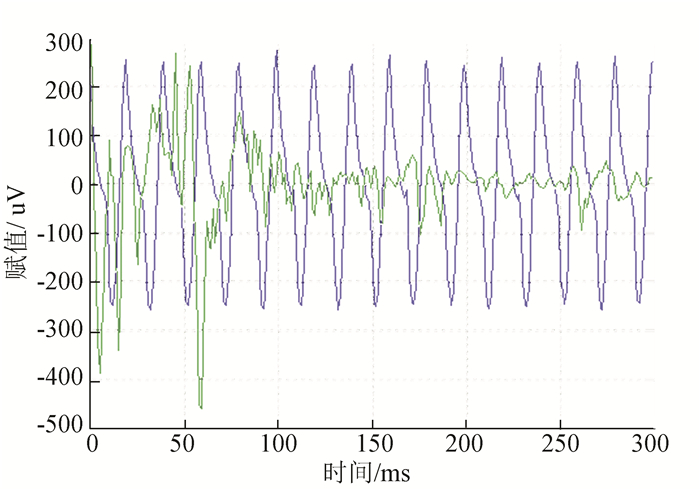
|
图 8 仿真图像与判断结果 Figure 8 The simulation image and judging results |
计算皮尔逊相关系数的r数值为-0.094 8,p<0.05, 显著性差异明显,根据皮尔逊相关系数r是统计学概念,表明了模版信号与一般人正常步态信号的相关度极低。在图 8中,2个信号的波形也完全不重叠且有较大差异,佐证了模版信号与被测信号没有相关度。判断语句显示了被测信号不是痉挛信号,给出了正确的结果。证明了本文运用的算法在识别不是痉挛信号时是可行的。
5 结论1) 综合上述各组的实验仿真情况,发现以皮尔逊相关系数作为理论依据的基于波形形状的模版匹配算法,在将采集到的痉挛表面肌电信号和正常人的表面肌电信号导入MATLAB系统中,进行仿真实验后。得到了痉挛信号的判断结果,判断出了个人专属模版信号在病人判断痉挛中的可行性。可以得出基于形状的模版匹配算法在同一患者的痉挛识别上有较高的准确性,能基本达到预设的效果。
2) 但由于个体的表面肌电信号的差异性,算法目前无法通过一个共用模版准确的识别不同患者的痉挛信号,不同的患者需要使用自身采集的模版信号。算法有一定病人依赖性(patient-depend)。一般情况下正常步态肌电信号与痉挛信号相关度极小,因此不会出现将正常信号识别成痉挛信号的情况。当然对于模版适用性的问题,目前有两个解决方案。一是通过大量的数据采集,进行大量的仿真实验来逐渐优化模版,并最终得到一个通用性的模版信号;二是将模版信号与被测型号进行二次的数据处理,提高周期在形状相似度中的比重,减少幅值的影响。
| [1] |
刘青, 曹建国, 贠国俊. 体外冲击波疗法在肌肉痉挛治疗中的应用[J]. 中国康复, 2014, 29(1): 65-67. LIU Qing, CAO Jianguo, YUN Guojun. Extracorporeal shock wave therapy in the treatment of muscle spasm[J]. Chinese Journal of Rehabilitation, 2014, 29(1): 65-67. DOI:10.3870/zgkf.2013.06.022 (  0) 0) |
| [2] |
王智文, 蔡启先, 陈劲飙, 等. 利用肤色分割和自适应模版匹配的人脸检测[J]. 广西工学院学报, 2013, 24(1): 1-8. WANG Zhiwen, CAI Qixian, CHEN Jinbiao, et al. Face detection using skin-color segmentation and adaptive template matching[J]. Journal of Guangxi University of Technology, 2013, 24(1): 1-8. DOI:10.3969/j.issn.1004-6410.2013.01.001 (  0) 0) |
| [3] |
卜凡艳. 数字图像匹配技术研究[D]. 合肥: 合肥工业大学, 2010. PU Fanyan. Research on thetechniques of digital image matching[D]. Hefei: Hefei University of Technology, 2010. http://d.wanfangdata.com.cn/Thesis/Y1700917 (  0) 0) |
| [4] |
袁琦. 癫痫脑电的分类识别及自动检测方法研究[D]. 济南: 山东大学, 2014. YUAN Qi. Research on epileptic EEC identificatian and automatic seizure detectiong[D]. Jinan:Shandong University, 2010. http://d.wanfangdata.com.cn/Thesis/Y2597906 (  0) 0) |
| [5] |
江依法, 周青, 陈伟燕. 一种改进的模板匹配算法及其在ECG波形识别中的应用[J]. 中国生物医学工程学报, 2012, 31(5): 775-780. JIANG Yifa, ZHOU Qing, CHEN Weiyan. An improved template-matching algorithm and its application in ECG waveform recognition[J]. Chinese Journal of Biomedical Engineering, 2012, 31(5): 775-780. DOI:10.3969/j.issn.0258-8021.2012.05.019 (  0) 0) |
| [6] |
李宏彬, 赫光中, 果秋婷. 基于皮尔逊相关系数的有机质谱相似性检索方法[J]. 化学分析计量, 2015, 24(3): 33-37. LI Hongbin, HE Guangzhong, GUO Qiuting. Similarity retrieval method of organic mass spectrometry based on the pearson correlation coefifcient[J]. Chemical Analysis and Meterage, 2015, 24(3): 33-37. DOI:10.3969/j.issn.1008-6145.2015.03.009 (  0) 0) |
| [7] |
车远宏, 贾雍, 汤卓, 等. 皮尔逊相关系数在风电功率组合预测中的应用[J]. 广西电力, 2016, 39(3): 50-53. CHE Yuanhong, JIA Yong, TANG Zhuo, et al. Application of pearson correlation coefficient in wind power combination prediction[J]. Guangxi Electric Power, 2016, 39(3): 50-53. DOI:10.3969/j.issn.1671-8380.2016.03.013 (  0) 0) |
 2017, Vol. 15
2017, Vol. 15


