蛋白质折叠问题,是生命科学领域的前沿课题之一。蛋白质折叠类型反映了蛋白质的核心二级结构单元的连接方式[1]。包括二级结构单元(如螺旋、折叠等)、二级结构单元的相对排布位置关系、蛋白质多肽链的整个路由关系等蛋白质分子空间结构组成的3个方面。对自然界存在的数千种折叠类型进行系统分类和识别,探索蛋白质折叠形成的经验规律,将有助于揭示蛋白质的折叠规律,为精确的蛋白质三级结构预测提供基础。
蛋白质三级结构复杂而不规则,但其所对应的蛋白质折叠类型却只有数百到数千种[2],蛋白质折叠类型分类是蛋白质折叠折叠首先需要解决的基本问题。SCOP数据库[3-5]是应用最广泛的结构分类数据库,为层状结构,包括蛋白质结构类、折叠类型、超家族、家族等不同层次,与蛋白质折叠类型对应的是fold层次,它是在超家族的基础上,按照二级结构及其空间分布及拓扑连接,根据专家经验人工完成折叠类型的指认。2013年,在SCOP已有分类的基础上,SCOPe[6]数据库建立。尽管SCOPe中部分蛋白质样本通过序列比对可自动获得分类结果,但所用自动分类结果与手动分类结果并不相同。新发布的ASTRAL现在依然使用SCOP中的手动分类结果。最近7年,SCOP数据中折叠层所包含的折叠类型总数基本保持在1 393种左右,4种主要结构类包含的折叠类型总数保持在1 000种左右,折叠类型总数基本稳定。对已有SCOP的人工分类结果进行数据挖掘、建立蛋白质折叠类型分类方法,实现蛋白质折叠类型的自动分类,是迫切需要解决的问题。
模板的选取是建立蛋白质折叠类型分类方法的基础,也直接左右了分类结果的好坏[7]。通常会选取一个结构冗余少、折叠核心清晰的天然蛋白质作为折叠类型模板[8-10]。结构冗余少、折叠核心清晰的天然蛋白质主要靠人工凭经验挑选,不同的模板挑选结果会影响蛋白质折叠类型分类结果[9];同时,对部分家族、超家族数量较多的蛋白质折叠类型,以一个以结构简单的天然样本作为模板的分类结果并不理想[8-10],其原因是由于家族及超家族的分布比较宽泛,使得单一模板无法表现不同家族及超家族的共同特征,即普适性不够,需要多模板才能解决问题。如何克服人工挑选模板的局限性及对部分折叠类型单模板的普适性问题,迫切需要设计反应蛋白质折叠类型共同特征的单模板或多模板来解决上述问题。
本文将在前期工作基础上[10-12],提出系统的蛋白质折叠类型模板设计方法,对SCOP数据库4种主要结构类的近千种蛋白质折叠类型进行模板设计建模,形成完成蛋白质折叠类型模板数据库,利用成熟的结构比对方法——TM-align和打分函数——TM-score,建立基于设计模板的蛋白质折叠分类的分类方法,解决SCOP数据库的自动分类问题。
1 材料本课题主要选取Astral SCOPe 2.05数据库中相似性小于40%,且分辨率高于25 nm的All alpha proteins(α),All beta proteins (β),Alpha and beta proteins (α/β),Alpha and beta proteins (α+β)4类蛋白所属的折叠类型为研究对象,其中共有989种折叠类型、12 165个样本,相应数据记为Set-Ⅰ。表 1列举了4类蛋白包含的折叠类型数目、家族数目以及样本数目。
| 表 1 4类蛋白包含的折叠类型、家族及样本数目 Table 1 Number of folding type, family and sample of four class |
实验集中,有359种蛋白质折叠类型仅包含一个家族,且家族中仅包含一个样本,对于这部分折叠类型,需要利用Astral SCOPe 2.05数据库中相似性小于95%的数据信息,相应数据记为Set-Ⅰ-1;其余630种蛋白质折叠类型含有两个及两个以上家族,对应的家族数及样本数分别为3 582、11 806,相应数据记为Set-Ⅰ-2。
独立检验集:SCOPe astral 2.06数据库[6]中剔除SCOPe astral2.05所含样本,余下2 142样本,涉及368种蛋白质折叠类型,记为Set-Ⅱ。
2 蛋白质折叠类型模板设计及模板数据库的构建蛋白质折叠类型的分类以蛋白质折叠核心的规则结构片段组成、连接和空间排布为依据,其中的规则结构片段即α-螺旋或β-折叠,其骨架结构主要由α-碳原子连接而形成。因此折叠类型模板的设计就是确定折叠核心的片段并对其骨架结构的α-碳原子坐标进行建模。
2.1 家族模板设计方法及家族模板数据库以BRD-like折叠类型模板设计方法[12]为基础并修改完善,建立系统的家族模板设计方法。具体步骤为:对家族样本利用MUSTANG[13]进行多结构比对,获得多结构比对信息;提取多结构比对信息中完全匹配的片段(即家族样本共同参与的折叠核心片段),形成该家族模板的折叠核心结构;对折叠核心片段进行骨架结构建模(即提取骨架坐标信息),形成家族模板。
骨架坐标提取方法:对由n个样本组成的家族,利用MUSTANG进行多结构比对,获得多结构比对结果,提取完全匹配片段,对匹配片段中任一残基i的α-碳原子匹配坐标信息——(xi, yi, zi),计算匹配坐标的平均值——(x, y, z),将其作为该残基的骨架α-碳坐标信息,形成匹配片段的骨架坐标信息。求坐标平均值公式如下:
| $ \begin{array}{l} \bar x = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}}, \\ \bar y = \frac{1}{n}\sum\limits_{i = 1}^n {{y_i}}, \\ \bar z = \frac{1}{n}\sum\limits_{i = 1}^n {{z_i}} . \end{array} $ |
利用MUSTANG[13]进行程序蛋白质多样本的多结构比对,是因为与POSA[14]、CE-MC[15]、MALECON[16]和MultiProt[17]等多结构比对软件相比,该软件它在空间折叠、残基的接触模式中有较强的识别能力。
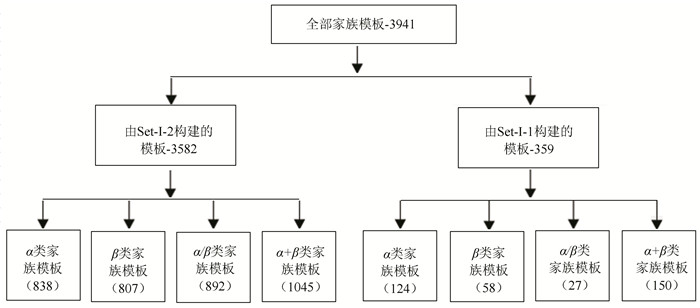
利用上述方法,对989种蛋白质折叠类型涵盖的3 941家族分别构建家族模板,形成蛋白质家族模板数据库。数据库中的家族模板编号为SCOPe astral中相应家族代码,模板在4种结构类中的分布如图 1所示。
|
图 1 家族模板数据库分布 Figure 1 Database distribution diagram of family template |
蛋白质折叠类型模板是以家族模板为单位通过系统聚类并经过筛选和验证最终得到。系统聚类的基本思想:对任意蛋白质折叠类型所属的n个家族模板,先将n个家族模板看成不同的n类,然后将性质最接近(距离最近)的两类合并为一类,再从n-1类中找到最接近的两类加以合并,依此类推,直到所有的家族模板被合为一类,得到n个家族模板的系统聚类图。家族模板通过TM-align[18]进行两两比对,以TM-score[19]作为距离参数,将TM-score取值最大(即距离最小)的两家族合并,合并方法与模板数据库的蛋白质折叠类型分类方法相同。
在Bromodomain-like折叠类型模板的设计基础上[12],并通过对系统聚类图中节点对应初始模板的计算分析及检验,提出任意蛋白质折叠类型i模板筛选的经验标准:具有折叠类型i特有全部折叠核心片段;分布于系统聚类图中的独立分支;由家族模板首次合并形成;对蛋白质折叠类型i所属样本的识别率不低于80%。
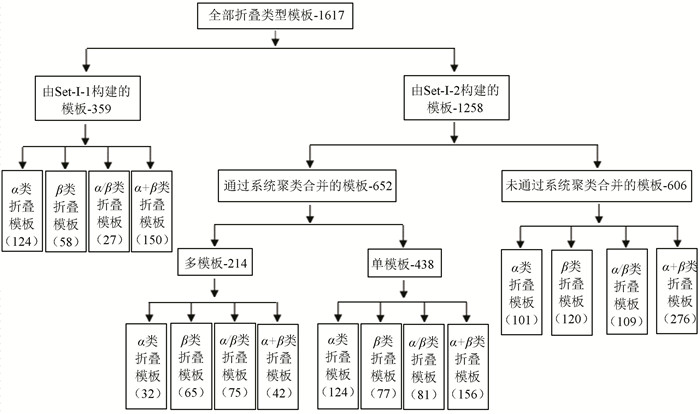
利用上述方法,对989种蛋白质折叠类型分别构建模板,组成折叠类型模板数据库,模板分布如图 2所示。其中,由数据集Set-Ⅰ-1构建的模板359种,由于这些蛋白质折叠类型仅含一个家族,家族模板即为折叠类型模板;由数据集Set-Ⅰ-2构建的模板数共1 258,其中508种蛋白质折叠类型成功筛选到了模板,另外的122种折叠类型未能筛选到满足条件的模板,以家族模板替代折叠类型模板。
|
图 2 折叠类型模板数据库分布 Figure 2 Database distribution diagram of folding type template |
蛋白质折叠类型模板的具体数据信息,见表 2。Fold代表折叠类型,Number of template代表每种折叠类型中模板的数量,Mode-ID为编号,TM-score为合并家族模板的打分值。以b.1.5.1 _29.8为例,其中b代表结构类,即全β类,1代表SCOP数据库中全β类的折叠类型,5.1_29.8代表形成该模板的5.1和29.8家族,相应的TM-score列对应的单元格为空。
| 表 2 折叠类型模板的具体信息 Table 2 Specific information about folding type templates |
由表 2可知,折叠类型模板识别率及TM-score的平均值分别为96.17%、0.83,模板的平均识别率明显高于筛选标准,由此说明,模板本身抓住了折叠类型的基本特征,模板设计具有合理性及适用性。
3 模板数据库的蛋白质折叠类型分类方法及结果 3.1 模板数据库的蛋白质折叠类型分类方法将任意待测蛋白样本与模板数据中的所有模板进行TM-align[18]比对,计算TM-score[19]值。TM-score取值最大的模板所在的折叠类型即为待测蛋白样本所属折叠类型。
分类结果利用敏感性、特异性、Matthew相关系数3个指标对其进行评估,参数定义如下:
| $ \begin{array}{l} 敏感性\;{S_n} = \frac{{{t_p}}}{{{t_p} + {f_n}}} \times 100\%, \\ 特异性\;{S_p} = \frac{{{t_n}}}{{{t_n} + {f_p}}} \times 100\%, \\ {\rm{MCC}} = \frac{{\left( {{t_p} \times {t_n}} \right)-\left( {{f_p} \times {f_n}} \right)}}{{\sqrt {\left( {{t_p} + {f_n}} \right) \times \left( {{t_n} + {f_p}} \right) \times \left( {{t_p} + {f_p}} \right) \times \left( {{t_n} + {f_n}} \right)} }}. \end{array} $ |
式中: tp为真阳性个数; tn为真阴性个数; fp为假阳性个数; fn为假阴性个数。
3.2 自洽性检验为验证模板设计及分类方法的合理性,以数据集Set-Ⅰ中的样本为研究对象,分别利用家族模板数据库与折叠类型模板数据库进行蛋白质折叠类型分类的自洽性检验,检验结果见表 3、4。其中S表示折叠类型所含样本数量,S′为真阳性与假阳性数量之和。
| 表 3 家族模板的自洽性检验 Table 3 Self consistency test of family template |
| 表 4 折叠类型模板的自洽性检验 Table 4 Self consistency test of folding type template |
由检验结果可知,基于家族模板数据库自洽性检验结果的敏感性、特异性及MCC的均值分别高达95.00%、99.99%、0.94,基于折叠类型模板数据库自洽性检验结果的敏感性、特异性以及MCC的均值分别为93.71%、99.97%及0.91。两种类型模板对相同数据集的分类检验结果相当,前者的分类结果略高于后者。说明家族模板及折叠类型模板设计合理,模板反映了折叠类型的基本特征;前者的模板总数为3 941,后者仅为1 617,后者模板数仅为前者的2/5,分类速度后者远远优于前者,分类精度家族模板略优于折叠类型模板。
3.3 独立性检验为进一步检验模板数据库及分类方法的普适性,以数据集Set-Ⅱ中的样本为研究对象,分别对家族模板数据库与折叠类型模板数据库进行独立性检验,检验结果见表 5、6。S+为数据集Set-Ⅱ中样本数量。
| 表 5 家族模板的独立性检验 Table 5 Independence test of family template |
| 表 6 折叠类型模板的独立性检验 Table 6 Independence test of folding type template |
由表 5、6可知,家族模板数据库及折叠类型模板数据库对扩充样本的分类效果稍差于自洽性检验中的结果,但是在独立性检验中家族模板与折叠类型模板的分类效果普遍高于90%,说明模板数据库及其分类方法可用于对扩充蛋白样本进行折叠类型的分类,从而验证了模板设计及分类方法具有有效的普适性。
4 结论蛋白质折叠规律研究是生命科学重大前沿课题,折叠分类是蛋白质折叠研究的基础,折叠分类也将应用到蛋白质识别中去。本文基于Astral SCOPe 2.05数据库中相似性小于40%的α、β、α+β及α/β所属的折叠类型为研究对象,通过对蛋白质折叠结构分析及信息挖掘,完善了蛋白质折叠类型模板设计方法,完成家族模板数据库及折叠类型模板数据库的构建,建立基于模板的蛋白质折叠类型分类方法,并用于蛋白质折叠类型的自动化分类。结果表明:1) 模板设计方法合理,并可用于家族及折叠类型模板的构建;2) 构建了完整的α、β、α/β以及α+β等4类蛋白所包含折叠类型模板数据库及家族模板数据库;3) 蛋白质折叠类型分类方法能够有效对已知结构的蛋白进行折叠类型的归类。
致谢 本课题能够顺利完成,首先,感谢北京市自然科学基金资助项目的大力支持;其次,衷心的感谢导师李晓琴教授的悉心指导,从文章的选题、研究计划的制定,各个方面都离不开李老师热情耐心的帮助和教导;最后,感谢实验室的同学们对我提供的帮助。
| [1] |
FINKELSTEIN A V, PTITSYN O B. Why do globular proteins fit the limited set of folding patterns[J]. Progress in Biophysics & Molecular Biology, 1987, 50(3): 171–190.
DOI:10.1016/0079-6107(87)90013-7( 0) 0)
|
| [2] |
CHOTHIA C. Proteins. One thousand families for the molecular biologist[J]. Nature, 1992, 357(6379): 543–544.
DOI:10.1038/357543a0( 0) 0)
|
| [3] |
ANDREEVA A, HOWORTH D, BRENNER S E, et al. SCOP database in 2004: refinements integrate structure and sequence family data[J]. Nucleic Acids Research, 2004, 32(Suppl-1): D226–D229.
DOI:10.1093/nar/gkh039( 0) 0)
|
| [4] |
GANDHIMATHI A, GHOSH P, HARIHARAPUTRAN S, et al. PASS2 database for the structure-based sequence alignment of distantly related SCOP domain superfamilies: update to version 5 and added features[J]. Nucleic Acids Research, 2015, 44(D1): D410–D414.
DOI:10.1093/nar/gkv1205( 0) 0)
|
| [5] |
ANDREEVA A, HOWORTHD, CHANDONIA J M, et al. Data growth and its impact on the SCOP database: new developments[J]. Nucleic Acids Research, 2008, 36(Suppl-1): D419–D425.
DOI:10.1093/nar/gkm993( 0) 0)
|
| [6] |
FOX N K, BRENNER S E, CHANDONIA J M. SCOPe: Structural Classification of Proteins--extended, integrating SCOP and ASTRAL data and classification of new structures[J]. Nucleic Acids Research, 2014, 42(D1): D304–D309.
DOI:10.1093/nar/gkt1240( 0) 0)
|
| [7] |
KELLEY L A, MACCALLUM R M, STEMBERG M J. Enhanced genome annotation using structural profiles in the program 3D-PSSM[J]. Journal of Molecular Biology, 2000, 299(2): 499–520.
DOI:10.1006/jmbi.2000.3741( 0) 0)
|
| [8] |
马帅, 王勤, 李晓琴. α/β类蛋白质折叠类型的分类方法研究[J]. 生物信息学, 2014, 12(2): 123–132.
MA Shuai, WANG Qin, LI Xiaoqin. The study of classification of protein folding types of α/β[J]. China Journal of Bioinformatics, 2014, 12(2): 123–132. DOI:10.3969/j.issn.1672-5565.2014.02.08(  0) 0)
|
| [9] |
孔令强, 李晓琴. 基于特征片段信息的PH domain-like barrel蛋白质折叠类型分类方法[J]. 生物信息学, 2012, 10(2): 125–129.
KONG Lingqiang, LI Xiaoqin. A method of PH domain-like barrel protein fold classification based on characteristic fragments[J]. China Journal of Bioinformatics, 2012, 10(2): 125–129. DOI:10.3969/j.issn.1672-5565.2012.02.13(  0) 0)
|
| [10] |
李晓琴, 仁文科, 刘岳, 等. 蛋白质折叠类型分类方法及分类数据库[J]. 生物信息学, 2010, 8(3): 245–253.
LI Xiaoqin, REN Wenke, LIU Yue, et al. Protein fold type classify methods and classification database[J]. China journal of Bioinformatics, 2010, 8(3): 245–253. DOI:10.3969/j.issn.1672-5565.2010.03.015(  0) 0)
|
| [11] |
LUO Liaofu, LI Xiaoqin. Recognition and architecture of the framework structure of protein[J]. Proteins Structure Function & Bioinformatics, 2000, 39(1): 9–25.
DOI:10.1002/(SICI)1097-0134(20000401)39:1<9::AID-PROT2>3.3.CO;2-C( 0) 0)
|
| [12] |
李晓琴, 张春城. Bromodomain-like折叠类型模板的设计[J]. 北京工业大学学报, 2016, 42(10): 1572–1580.
LI Xiaoqin, ZHANG Chuncheng. Design of folding type template of Bromodomain-like[J]. Journal of Beijing University of Technology, 2016, 42(10): 1572–1580. DOI:10.11936/bjutxb2015100078(  0) 0)
|
| [13] |
KONAGURTHU A S, WHISSTOCK J C, STUCKEY P J, et al. MUSTANG: a multiple structural alignment algorithm[J]. Proteins Structure Function & Bioinformatics, 2006, 64(3): 559–574.
DOI:10.1002/prot.20921( 0) 0)
|
| [14] |
YE Y, GODZIK A. Multiple flexible structure alignment using partial order graphs[J]. Bioinformatics, 2005, 21(10): 2362–2369.
DOI:10.1093/bioinformatics/bti353( 0) 0)
|
| [15] |
GUDA C, LU S, SCHEEFF E D, et al. CE-MC: a multiple protein structure alignment server[J]. Nucleic acids research, 2004, 32(suppl 2): W100–W103.
DOI:10.1093/nar/gkh464( 0) 0)
|
| [16] |
OCHAGAVIA M E, WODAK S. Progressive combinatorial algorithm for multiple structural alignments: application to distantly related proteins[J]. Proteins Structure Function & Bioinformatics, 2004, 55(2): 436–454.
DOI:10.1002/prot.10587( 0) 0)
|
| [17] |
SHATSKY M, NUSSINOV R, WOLFSON H J. MultiProt-a multiple protein structural alignment algorithm[J]. Lecture Notes in Computer Science, 2002, 2452: 235–250.
DOI:10.1007/3-540-45784-4_18( 0) 0)
|
| [18] |
ZHANG Yang, SKOLNICK J. TM-align: a protein structure alignment algorithm based on the TM-score[J]. Nucleic Acids Research, 2005, 33(7): 2302–2309.
DOI:10.1093/nar/gki524( 0) 0)
|
| [19] |
XU Jinrui, ZHANG Yang. How significant is a protein structure similarity with TM-score = 0.5?[J]. Bioinformatics, 2010, 26(7): 889–895.
DOI:10.1093/bioinformatics/btq066( 0) 0)
|
 2017, Vol. 15
2017, Vol. 15


