全基因组代谢网络(Genome-scale metabolic models,GEMs)是以基因组学数据为基础,在高通量测序技术支持下整合基因相关的组学信息,并结合文献中的知识,最终得到生物细胞中生化反应的全局网络。第一个全基因组代谢模型是细菌H. influenzae的代谢模型,构建于1999年,包括343个代谢物和488个代谢反应[1]。截止2016年3月,在基因组代谢网络数据库(GSMNDB)中已发布了116个物种的135个全基因组代谢网络模型(http://synbio.tju.edu.cn/GSMNDB/Pages/Models.htm)。
全基因组代谢网络分析指利用相关代谢网络分析技术并结合相关生物学知识对代谢网络进行生物学分析的过程。其中预测细胞内特定功能生化反应流量分布并确定关键反应是全基因组代谢网络分析的重点。
代谢网络中代谢物物质量数据获取的方法主要是通过碳同位素标记法,该方法对代谢物中的碳元素进行标记,使用质谱仪或者核磁共振仪对标记的代谢物进行检测,根据测量强度的变化得到细胞内的代谢流量分布[2, 3]。此类实验数据的不断增多为代谢网络流量的计算机模拟分析提供了基础。
1 代谢网络分析—流量平衡分析方法代谢流量计算机模拟分析的经典方法是代谢流量平衡分析方法(Flux Balance Analysis,简称FBA)[4]。该方法假定代谢网络反应状态达到准稳定状态时每一个中间反应物产生与消耗的物质量相等,如公式(1)所示,其中x代表代谢物的物质量,t代表特定时刻。
| $\frac{dx}{dt}=0$ | (1) |
FBA旨在找出准稳态条件下使细胞内某一目标函数Z=vb最优的可行解集。基于线性规划的原理,求解过程存在两种形式的约束条件,一种是等式约束,即在稳定状态下代谢物的输出与输入的代谢流量矢量和为0。假设代谢网络中的每一个节点代表的是一个反应物,每一条线代表一个生化反应。设定S为网络的化学计量矩阵(以反应物为行,生化反应为列),v为平衡时每一生化反应的流量。则平衡条件约束为公式(2)。
| $S.v=0$ | (2) |
另一种是不等式约束,即每一生化反应的代谢流量存在上下限vmin≤v≤vmax。根据这两个约束条件可求得流量v的基本解空间,利用线性规划算法(Linear Programming,LP)或混合线性优化算法(Mixed-integer linear programming,MILP)计算Z达到最大值时整个网络的流量分布值。
FBA方法自提出便成为研究代谢流量的基础方法,一般用来研究微生物的成长特性,解释生长表型以及预测特定环境下的关键反应[5]。随着对代谢网络研究的日渐深入,研究者尝试在FBA方法中增加额外的生物学约束条件,以得到更为准确的预测结果。这方面的研究主要包括三个方面:一是改进目标函数,或者增加目标函数。典型的方法有最小化代谢调整方法(Minimization Of Metabolic Adjustment,MOMA)[6]和最小调控控制方法(Regulatory On /Off Minimization,ROOM)[7];二是加入更多的约束条件(如,热力学信息),使得模拟过程更加接近于环境内部原则,如动态流量平衡分析(Dynamic Flux Balance Analysis,DFBA)[8]方法,Willemsen等人在DFBA的基础上进一步提出的修正方法——MetDFBA[9]。三是多水平最优化,即同时改进目标函数和增加约束条件,如OptStrain方法和OptKnock[10]方法等。
随着高通量测序技术的快速发展,对代谢网络的认识越来越深刻,对代谢反应的调控机制分析也越来越深入。以全基因组代谢网络为基础,整合基因表达数据集对网络进行FBA分析的方法可以更精确的模拟细胞内代谢变化,提高代谢模型预测的准确性。
2 整合转录组学数据的代谢网络分析基因表达在不同条件下呈现不同的表达状态[11],而基因表达过程与代谢过程密切相关。基因表达数据反映基因的转录产物mRNA的相对或绝对丰度,有研究表明转录mRNA的浓度与生化反应催化剂酶的浓度有很强的相关性[12, 13]。转录组学数据的获取方法主要有cDNA微阵列和寡聚核苷酸芯片技术等。目前,采用基因芯片技术已获得海量的转录组学数据。利用各种整合方法模拟基因表达与代谢反应之间的联系是该类方法研究的重点。
FBA改进方法一般是在流量平衡约束基础上添加额外信息约束解空间或改变目标函数以更好的描述细胞代谢情况,并尝试通过多水平的最优化方法提高模拟的准确性。研究利用基因表达信息约束解空间一直是其中的焦点。2004年第一次开始整合转录组学数据对代谢网络进行约束,近十年来研究者们提出各种与实际应用相结合的方法[14-26],整合多组学数据对代谢网络进行FBA分析已经成为一种趋势。因而,本文总结了几种整合基因表达信息求解代谢流量的方法并分析了几种方法在判定基因表达状态时的不同策略。
2.1 设定先验阈值判定基因表达状态Åkesson等于2004年提出整合基因表达数据对全基因组代谢网络进行约束的方法,他们根据生化反应中酶所对应基因的表达情况判断反应是否发生[27]。他所使用的表达数据来源于寡核苷酸芯片,检测到基因表达的信号则表示对应的生化反应发生,若反应相关的多个基因均不表达则对应反应不发生,反应流量值置为0。通过这种方法进一步约束了FBA分析中流量v的解空间。该方法最早将多组学数据整合进代谢研究,为后续研究提供了一种新的思路。应用该方法,成功预测了葡萄糖为生长底物时酵母菌在无氧和有氧情况下的生长情况。但该方法判断基因是否表达的方式过于简单,同时因芯片的检测灵敏度较低而产生较多误差。
第一种整合方法由于数据处理粗糙,在判定基因表达状态时可能会遗漏表达量小但细胞完成功能必须的反应。根据特定条件下代谢功能的差异,Becker提出了GIMME (Gene Inactivity Moderated by Metabolism and Expression)方法,模拟了细胞在特定条件下能够行使特定的功能[28]。其思路是删除在特定条件下的不重要生化反应通路,同时增加一些功能反应通路,以得到特定条件下能完成特定功能的高效代谢网络模型。该方法可分为两个步骤:首先设定基因表达阈值,比较酶对应基因的表达值,将低于该阈值的酶催化的生化反应从代谢网络中删除,从而得到一个削减的代谢网络。第二步,将特定环境中细胞生长功能代谢模型(Required Metabolic Functionalities,RMF)中包含的反应加到第一步得到的模型中,得到初步的特定条件下的网络模型。使用积分函数计算不一致得分来评价不同表达阈值下所得到代谢流量分布是否合适,不一致得分值越小表示网络完成的功能越好。该方法的表达阈值需要用户提前设定并不断调整以得到最好的模拟结果。Schmid等在此方法的基础上提出了改进的GIM3E(Gene Inactivation Moderated by Metabolism,Metabolomics and Expression)方法[29],同时考虑代谢网络中可逆生化反应的优化问题,并成功应用于预测沙门氏菌在不同生长环境下的代谢过程。
上述方法对基因表达阈值的选取进行评价并不断修正以拟合真实数据,Chandrasekaran和Price对于酶基因是否表达的判断依据进行了改进,提出了代谢概率调控方法PROM (Probabilistic Regulation Of Metabolism)[30]。该方法分析全基因组基因表达微阵列数据,构建由转录因子及其调控基因构成的基因调控网络。由特定条件得到转录因子B的状态,并由先验知识设定表达阈值,计算同一条件下多个表达数据集得到基因A的状态,基因A表达且转录因子起作用的概率P(A=1|B=1)大于0.5则对应酶所催化的生化反应发生,如此判断各个反应的状态进而对代谢网络中的生化反应进行约束。该方法需要通过分析大量的实验数据来确定转录因子和靶基因表达的关系进而确定基因状态。与Åkesson等的方法相似,该方法本质上是在特定条件下删除网络中生化反应通路达到精简网络的目的。
上述方法共同点是均依赖于先验阈值的选取。其中PROM利用多个条件的均值增加阈值选择的可信度,GIMME和GIM3E方法使用积分函数衡量阈值选取可信度。但初次选取的阈值对后续操作至关重要。另外一些方法使用数据之间的内在关系选取相对高表达和低表达的基因。这种方法可以在先验知识缺乏的情况下发挥作用,有一定的使用价值。
2.2 计算相对阈值判定基因表达状态Hadas等提出的iMAT方法比较全部基因表达数据并设置阈值(均值±方差)将基因表达值离散化为低、中、高三种状态,分别用(-1/0/1)表示[31]。并分别对三种状态的反应上下限增加约束,在提高高表达基因对应反应比例同时通过积分函数计算反应状态与表达数据相一致程度。最终找到与表达数据相一致的特定条件下的代谢网络。 Rossell等在iMAT方法基础上提出了EXAMO(The EXploration of Alternative Metabolic Optima)[32]方法,EXAMO方法选定全部基因中表达量从高到低排列在前15%的为高表达基因,后15%的为低表达基因,其余为中等表达基因,并在iMAT方法基础上构建不同条件下的反应得分,尝试构建特定环境下的代谢模型。该方法还能最小化整体的流量之和并将对应流量都由高表达基因对应的生化反应所携带,进而预测特定环境下的流量。
上述两种方法对基因状态的判定是相对于整体基因表达情况,EXAMO在先验知识缺乏的前提下构建特定代谢模型依赖于反应得分函数评价反应的判定与测得表达数据之间的相关性,期望找到最符合表达数据的表达情况。另外一些方法使用不同条件表达数据之间的比较关系得出不同条件下的可能代谢情况,例如Jensen等提出了MADE方法(Metabolic Adjustment by Differential Expression)[33]。MADE方法对不同条件下的表达数据进行t检验分析。设定必须发生反应对应状态为1,利用不同条件下的表达差异显著性判断不同条件下的其他基因表达状态。得到基因表达状态后预测对应生化反应开启或者关闭,得到特定条件下的适应性网络模型,最终应用于FBA分析。本质上,MADE方法通过考察不同条件下基因表达的差异程度判断基因的表达状态。使用该方法准确预测了酵母菌在葡萄糖生长环境下,在有氧和无氧生长条件的不同时间段基因表达的情况以及代谢模型的改变。
上述方法的共同点是使用基因表达数据之间相对比较的方法得到基因的表达状态,并进一步约束代谢网络。但也有差异,MADE方法将计算得到的基因状态集状态为0的反应直接删除,可能会由于前期预处理过程导致后期删除反应的误差。iMAT和EXAMO相对提高高表达基因集对应生化反应并降低低表达基因集对应生化反应,在一定程度上可以避免此类误差,但是准确性依赖于得分函数的选取与计算。
2.3 拟合函数法整合基因表达状态与代谢网络最近几年新发展了一种使用判定函数的方法整合转录组学数据与代谢网络。有研究表明基因表达量与酶浓度之间的关系近似对数曲线[13],使用特定函数描述基因表达水平与酶浓度的相关关系,将结果用于约束代谢反应的流量上下限并对代谢网络的流量进行优化。Angione等提出了METRADE(MEtabolic and TRanscriptomics Adaptation Estimator)[34]方法,该方法对于网络优化的工作比较复杂,在整合转录组学数据方面采用公式3表示的方法。
| $\left\{ \begin{matrix} \varphi ={{\left( 1+\left| log\text{ }\left( {{y}_{i}} \right) \right| \right)}^{sgn({{y}_{i}}-1)}} & if {{y}_{i}}\in {{R}^{+}}\backslash \left\{ 1 \right\} \\ 1 & if=1 \\ \end{matrix} \right.$ | (3) |
其中sgn(yi-1)=(yi-1)/|yi-1|该函数中设定yi为基因表达数据,φ为相对应酶浓度,将函数值φ带入反应上下限υi≥υiminφ,υi≤υimaxφ并进行FBA分析得到特定环境下代谢流量的分布。Angione等使用该方法精确模拟了大肠杆菌在不同环境下多个目标代谢物同时得到优化时的代谢流量分布情况。2016年,METRADE方法的提出者在原方法基础上,在log (yi)前面添加方差参数,进一步优化函数拟合的结果并运用该方法成功重建了大肠杆菌的代谢网络[35]。
该类方法结合基因表达数据与代谢数据之间的关系构建函数尽力拟合真实的代谢情况,在大量数据的支持下能够实现高准确性的拟合,是一种新型的模拟方法,随着对转录与代谢之间模式的理解不断深刻,该方法将得到更广泛的应用。
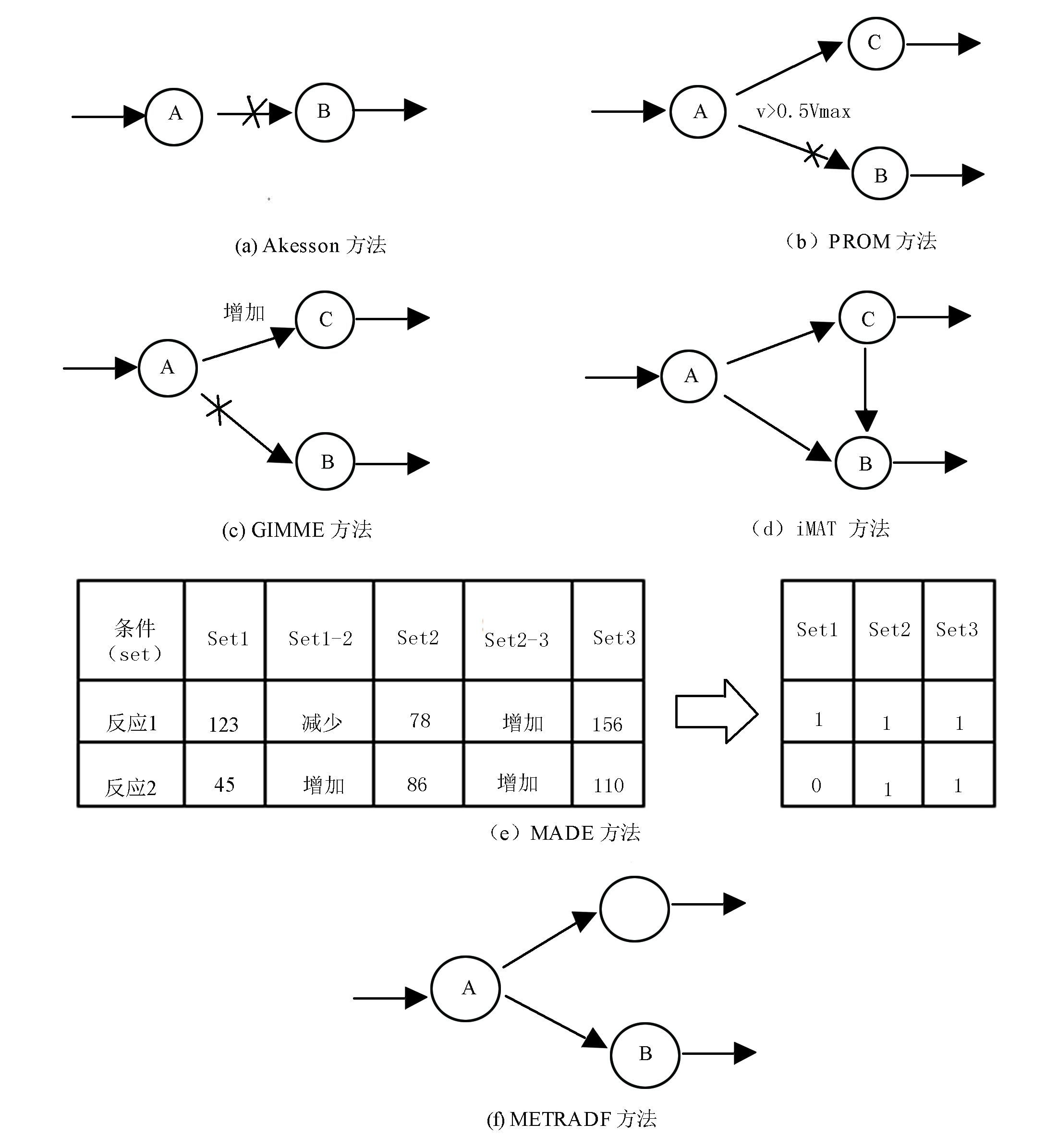
2.4 方法总结与比较整合基因表达数据进行代谢网络分析,其本质是对代谢网络的流量平衡分析添加约束条件。前面所述方法大部分是在进行FBA分析之前对网络进行调整,增加删除特定生化反应或调整网络结构以模拟特定条件下的真实情况。各种方法的简单示意如图 1所示。
|
图 1 改进的FBA网络分析方法差异比较分析 Figure 1 Comparative analysis diagram of improved FBA method |
图中节点A、B、C代表代谢物,连接线代表生化反应。(a) Åkesson 方法,直接检测反应对应基因表达值,X表示该反应从代谢网络中删除; (b) PROM方法,计算多次表达值的平均值,v>0.5Vmax则反应发生,反之不发生; (c)GIMME方法,设定阈值y,若A->B反应中酶对应基因表达值小于y,则删除该反应用X表示,并增加功能反应A->C,得到功能网络模型,设定得分函数判断y的合理性;(d) iMAT方法,计算得到中-低表达阈值y1,中-高表达阈值y2,得到不同反应对应状态,高表达对应反应rH,低表达对应反应rL。提高rH比例,同时降低rL比例;(e)MADE,方法采用t检验方法得到不同条件下基因表达状态;(f)METRADE方法,每一个生化反应的酶对应基因表达值不同时得到的酶的浓度不同,对应生化反应流量上下限不同,网络分析方法评价见表 1。
| 表 1 改进的FBA网络分析方法评价表 Table 1 Evaluation of improved FBA method |
本文介绍的方法代表整合转录组学研究代谢网络的大概发展思路,近年来各种整合转录组学数据进行代谢网络研究的实例涵盖微生物至人类的各个物种,2015年Shuyi等利用PROM方法构建地核杆菌的转录调控代谢网络并指导实验操作[36]。Tuulia等利用iMAT方法研究人类肝脏肿大的代谢机制[37]。Emrah等使用GIMME和MADE方法构建胶质母细胞瘤的特定全基因组代谢网络并预测癌症细胞代谢流量分布[38]。在应用上述方法的同时,一些研究者也在探索整合多种组学数据进行代谢网络研究。如Weihua等在FBA基础上整合多个组学数据进行代谢网络研究并解释细胞表型[39]。其他此类方面的应用还有很多[40-47]。由此可推断以代谢网络为基础,用系统生物学观点整合多组学数据研究细胞内代谢过程正成为一种常用方法。
3 总结与展望由于生物体内活动的复杂性,从系统生物学角度分析细胞内活动已经成为一种研究趋势,对细胞活动进行网络建模研究的方法也将愈加成熟。随着高通量数据的涌现,整合表达数据进入代谢网络已经成为改进FBA分析方法的主流思路。此类方法可分为两种模式,一种对代谢网络的结构进行直接调整,即通过表达数据判断相应的生化反应发生可能性,再进行FBA分析;另一种是在不改变原代谢网络的基础上,利用基因表达的数据和调控网络对优化过程进行限制。这些方法得出的结果大部分经过实验验证,有较大的应用价值。
但是本文所介绍方法整合数据相对单一,各方法均有其适用的局限性,方法准确度有待改进。目前的代谢网络研究也有待改进,首先,目前的代谢网络研究主体是整个细胞内网络,得到的是特定代谢途径的目标函数,细胞内的代谢子网络功能未被充分考虑;其次,基因表达与生化反应酶之间的关系比想象中复杂,多个基因共同调控生化反应的酶的机制目前尚不清楚。从MATRADE和omFBA方法[39]看出,未来从系统生物学角度研究代谢过程将是一个研究热点,整合多个层面的组学数据将更精确模拟细胞内代谢活动,整合方法的研究也将不断发展。
| [1] |
EDWARDS J S, PALSSON B O. Systems properties of the Haemophilus influenzae Rd metabolic genotype[J]. Journal of Biological Chemistry, 1999, 274(25): 17410–17416.
DOI:10.1074/jbc.274.25.17410 ( 0) 0)
|
| [2] |
ZAMBONI N, FENDT S M, RVHL M, et al. 13C-based metabolic flux analysis[J]. Nature Protocols, 2009, 4(6): 878–892.
DOI:10.1038/nprot.2009.58 ( 0) 0)
|
| [3] |
GARCA MARTN H, KUMAR V S, WEAVER D, et al. A method to constrain genome-scale models with 13C Labeling data[J]. PLoS Computational Biology, 2015, 11(9): e1004363.
DOI:10.1371/journal.pcbi.1004363 ( 0) 0)
|
| [4] |
ORTH J D, THIELE I, PALSSON B O. What is flux balance analysis?[J]. Nature Biotechnology, 2010, 28(3): 245–248.
DOI:10.1038/nbt.1614 ( 0) 0)
|
| [5] |
CHAPMAN S P, PAGET C M, JOHNSON G N, et al. Flux balance analysis reveals acetate metabolism modulates cyclic electron flow and alternative glycolytic pathways in chlamydomonas reinhardtii[J]. Frontiers in Plant Science, 2015(6): 474.
DOI:10.3389/fpls.2015.00474.eCollection2015 ( 0) 0)
|
| [6] |
SHLOMI T, BERKMAN O, RUPPIN E, et al. Regulatory on/off minimization of metabolic flux changes after genetic perturbations[J]. Proceedings of National Academy of Sciences of the United States of America, 2005, 102(21): 7695–7700.
DOI:10.1073/pnas.0406346102 ( 0) 0)
|
| [7] |
MAHADEVAN R, EDWARDS J S, DOYLE F R, et al. Dynamic flux balance analysis of diauxic growth in Escherichia coli[J]. Biophysical Journal, 2002, 83(3): 1331–1340.
DOI:10.1016/S0006-3495(02)73903-9 ( 0) 0)
|
| [8] |
GOMEZ J A, HOFFNER K, BARTON P I, et al. DFBAlab: a fast and reliable MATLAB code for dynamic flux balance analysis[J]. BMC Bioinformatics, 2014(15): 409.
DOI:10.1186/s12859-014-0409-8 ( 0) 0)
|
| [9] |
WILLEMSEN A M, HENDRICKX D M, HOEFSLOOT H C, et al. MetDFBA: incorporating time-resolved metabolomics measurements into dynamic flux balance analysis[J]. Molecular BioSystems, 2015, 11(1): 137–145.
DOI:10.1039/C4MB00510D ( 0) 0)
|
| [10] |
BURGARD A P, PHARKYA P, MARANAS C D, et al. Optknock: a bilevel programming framework for identifying gene knockout strategies for microbial strain optimization[J]. Biotechnology and Bioengineering, 2003, 84(6): 647–657.
DOI:10.1002/(ISSN)1097-0290 ( 0) 0)
|
| [11] |
卢汀. 生物信息学基因表达差异分析[J]. 生物信息学, 2014, 12(2): 140–144.
LU Ting. Bioinformatics analysis for gene differential expression[J]. Chinese Journal of Bioinformatics, 2014, 12(2): 140–144.
( 0) 0)
|
| [12] |
ANGIONE C, PRATANWANICH N, LIO P, et al. A hybrid of metabolic flux analysis and bayesian factor modeling for multiomic temporal pathway activation[J]. ACS Synthetic Biology, 2015, 4(8): 880–889.
DOI:10.1021/sb5003407 ( 0) 0)
|
| [13] |
VOGEL C, MARCOTTE E M. Insights into the regulation of protein abundance from proteomic and transcriptomic analyses[J]. Nature Reviews Genetics, 2012, 13(4): 227–232.
( 0) 0)
|
| [14] |
MEGCHELENBRINK W, ROSSELL S, HUYNEN M A, et al. Estimating metabolic fluxes using a maximum network flexibility paradigm[J]. PLoS One, 2015, 10(10): e139665.
( 0) 0)
|
| [15] |
PACHECO M P, JOHN E, KAOMA T, et al. Integrated metabolic modelling reveals cell-type specific epigenetic control points of the macrophage metabolic network[J]. BMC Genomics, 2015(16): 809.
DOI:10.1186/s12864-015-1984-4 ( 0) 0)
|
| [16] |
FERRAZZI F, MAGNI P, SACCHI L, et al. Inferring gene expression networks via static and dynamic data integration[J]. Studies in Health Technology and Informatics, 2006(124): 119–124.
( 0) 0)
|
| [17] |
SALAZAR M, VONGSANGNAK W, PANAGIOTOU G, et al. Uncovering transcriptional regulation of glycerol metabolism in Aspergilli through genome-wide gene expression data analysis[J]. Molecular Genetics and Genomics, 2009, 282(6): 571–586.
DOI:10.1007/s00438-009-0486-y ( 0) 0)
|
| [18] |
MOXLEY J F, JEWETT M C, ANTONIEWICZ M R, et al. Linking high-resolution metabolic flux phenotypes and transcriptional regulation in yeast modulated by the global regulator Gcn4p[J]. Proceedings of National Academy of Sciences of the United States of America, 2009, 106(16): 6477–6482.
DOI:10.1073/pnas.0811091106 ( 0) 0)
|
| [19] |
COLIJN C, BRANDES A, ZUCKER J, et al. Interpreting expression data with metabolic flux models: predicting Mycobacterium tuberculosis mycolic acid production[J]. PLoS Computational Biology, 2009, 5(8): e1000489.
DOI:10.1371/journal.pcbi.1000489 ( 0) 0)
|
| [20] |
VAN BERLO R J, DE RIDDER D, DARAN J M, et al. Predicting metabolic fluxes using gene expression differences as constraints[J]. IEEE/ACM Trans Computer Biology Bioinformatics, 2011, 8(1): 206–216.
DOI:10.1109/TCBB.2009.55 ( 0) 0)
|
| [21] |
LEE D, SMALLBONE K, DUNN W B, et al. Improving metabolic flux predictions using absolute gene expression data[J]. BMC Systems Biology, 2012(6): 73.
DOI:10.1186/1752-0509-6-73 ( 0) 0)
|
| [22] |
KIM J, REED J L. RELATCH: relative optimality in metabolic networks explains robust metabolic and regulatory responses to perturbations[J]. Genome Biology, 2012, 13(9): R78.
DOI:10.1186/gb-2012-13-9-r78 ( 0) 0)
|
| [23] |
COLLINS S B, REZNIK E, SEGRE D. Temporal expression-based analysis of metabolism[J]. PLoS Computational Biology, 2012, 8(11): e1002781.
DOI:10.1371/journal.pcbi.1002781 ( 0) 0)
|
| [24] |
TÖPFER N, JOZEFCZUK S, NIKOLOSKI Z. Integration of time-resolved transcriptomics data with flux-based methods reveals stress-induced metabolic adaptation in Escherichia coli[J]. BMC Systems Biology, 2012, 3(6): 148.
DOI:10.1186/1752-0509-6-148 ( 0) 0)
|
| [25] |
NAVID A, ALMAAS E. Genome-level transcription data of Yersinia pestis analyzed with a new metabolic constraint-based approach[J]. BMC Systems Biology, 2012, 3(6): 150.
DOI:10.1186/1752-0509-6-150 ( 0) 0)
|
| [26] |
WANG Y, EDDY J A, PRICE N D. Reconstruction of genome-scale metabolic models for 126 human tissues using mCADRE[J]. BMC Systems Biology, 2012, 3(6): 153.
DOI:10.1186/1752-0509-6-153 ( 0) 0)
|
| [27] |
AKESSON M, FORSTER J, NIELSEN J. Integration of gene expression data into genome-scale metabolic models[J]. Metabolic Engineering, 2004, 6(4): 285–293.
DOI:10.1016/j.ymben.2003.12.002 ( 0) 0)
|
| [28] |
BECKER S A, PALSSON B O. Context-specific metabolic networks are consistent with experiments[J]. PLoS Computational Biology, 2008, 4(5): e1000082.
DOI:10.1371/journal.pcbi.1000082 ( 0) 0)
|
| [29] |
SCHMIDT B J, EBRAHIM A, METZ T O, et al. GIM3E: condition-specific models of cellular metabolism developed from metabolomics and expression data[J]. Bioinformatics, 2013, 29(22): 2900–2908.
DOI:10.1093/bioinformatics/btt493 ( 0) 0)
|
| [30] |
CHANDRASEKARAN S, PRICE N D. Probabilistic integrative modeling of genome-scale metabolic and regulatory networks in Escherichia coli and Mycobacterium tuberculosis[J]. Proceedings of National Academy of Sciences of the United States of America, 2010, 107(41): 17845–17850.
DOI:10.1073/pnas.1005139107 ( 0) 0)
|
| [31] |
SHLOMI T, CABILI M N, HERRGARD M J, et al. Network-based prediction of human tissue-specific metabolism[J]. Nature Biotechnology, 2008, 26(9): 1003–1010.
DOI:10.1038/nbt.1487 ( 0) 0)
|
| [32] |
ROSSELL S, HUYNEN M A, NOTEBAART R A. Inferring metabolic states in uncharacterized environments using gene-expression measurements[J]. PLoS Computational Biology, 2013, 9(3): e1002988.
DOI:10.1371/journal.pcbi.1002988 ( 0) 0)
|
| [33] |
JENSEN P A, PAPIN J A. Functional integration of a metabolic network model and expression data without arbitrary thresholding[J]. Bioinformatics, 2011, 27(4): 541–547.
DOI:10.1093/bioinformatics/btq702 ( 0) 0)
|
| [34] |
ANGIONE C, LIÓ P. Predictive analytics of environmental adaptability in multi-omic network models[J]. Scientific Reports, 2015(5): 15147.
DOI:10.1038/srep15147 ( 0) 0)
|
| [35] |
ANGIONE C, CONWAY M, LI ÓP. Multiplex methods provide effective integration of multi-omic data in genome-scale models[J]. BMC Bioinformatics, 2016, 17(Suppl 4): 83.
DOI:10.1186/s12859-016-0912-1 ( 0) 0)
|
| [36] |
MA S, MINCH K J, RUSTAD T R, et al. Integrated modeling of gene regulatory and metabolic networks in Mycobacterium tuberculosis[J]. PLoS Computational Biology, 2015, 11(11): e100454311.
DOI:10.1371/journal.pcbi.1004543. ( 0) 0)
|
| [37] |
HYÖTYLÄINEN T, JERBY L, PETÄJÄ E M, et al. Genome-scale study reveals reduced metabolic adaptability in patients with non-alcoholic fatty liver disease[J]. Nature Communications, 2016(7): 8994.
DOI:10.1038/ncomms9994 ( 0) 0)
|
| [38] |
ÖZCANE, ÇAKıRT. Reconstructed metabolic network models predict flux-level metabolic reprogramming in Glioblastoma[J]. FRONTIERS IN NEUROSCIENCE, 2016(10): 156.
DOI:10.3389/fnins.2016.00156 ( 0) 0)
|
| [39] |
GUO W, FENG X. OM-FBA: integrate transcriptomics data with flux balance analysis to decipher the cell metabolism[J]. PLoS One, 2016, 11(4): e154188.
( 0) 0)
|
| [40] |
GARAY C D, DREYFUSS J M, GALAGAN J E. Metabolic modeling predicts metabolite changes in Mycobacterium tuberculosis[J]. BMC Systems Biology, 2015, 9(1): 57.
DOI:10.1186/s12918-015-0206-7 ( 0) 0)
|
| [41] |
T PFER N, JOZEFCZUK S, NIKOLOSKI Z. Integration of time-resolved transcriptomics data with flux-based methods reveals stress-induced metabolic adaptation in Escherichia coli[J]. BMC Systems Biology, 2012, 6(1): 1–10.
DOI:10.1186/1752-0509-6-1 ( 0) 0)
|
| [42] |
AGREN R, BORDEL S, MARDINOGLU A, et al. Reconstruction of genome-scale active metabolic networks for 69 human cell types and 16 cancer types using INIT[J]. PLoS Computational Biology, 2012, 8(5): e1002518.
DOI:10.1371/journal.pcbi.1002518 ( 0) 0)
|
| [43] |
FANG X, WALLQVIST A, REIFMAN J. Modeling phenotypic metabolic adaptations of Mycobacterium tuberculosis H37Rv under hypoxia[J]. PLoS Computational Biology, 2012, 8(9): e1002688.
DOI:10.1371/journal.pcbi.1002688 ( 0) 0)
|
| [44] |
YIZHAK K, GABAY O, COHEN H, et al. Model-based identification of drug targets that revert disrupted metabolism and its application to ageing[J]. Nature Communications, 2013(4): 2632.
DOI:10.1038/ncomms3632 ( 0) 0)
|
| [45] |
YIZHAK K, GAUDE E, LE DEVEDEC S, et al. Phenotype-based cell-specific metabolic modeling reveals metabolic liabilities of cancer[J]. eLIFE, 2014, 21(3): e03641.
DOI:10.7554/eLife.03641 ( 0) 0)
|
| [46] |
STEMPLER S, YIZHAK K, RUPPIN E. Integrating transcriptomics with metabolic modeling predicts biomarkers and drug targets for Alzheimers disease[J]. PLoS One, 2014, 9(8): e105383.
DOI:10.1371/journal.pone.0105383 ( 0) 0)
|
| [47] |
AGREN R, MARDINOGLU A, ASPLUND A, et al. Identification of anticancer drugs for hepatocellular carcinoma through personalized genome-scale metabolic modeling[J]. Molecular Systems Biology, 2014(10): 721.
DOI:10.1002/msb.145122 ( 0) 0)
|
 2016, Vol. 14
2016, Vol. 14


