2. 天津工业大学 数学科学学院 应用数学中心,天津 300387
2. School of Mathematical Sciences, Tiangong University, Tianjin 300384, China
哺乳动物体内的不同组织器官通过相应组织干细胞的自我更新和分化维持正常的组织细胞数量与生理功能[1-2]。在这个过程中,干细胞受控的增殖分化对于生命体的生长、发育、衰老、组织修复等过程中起着重要作用,干细胞的异常增殖会导致恶性肿瘤、肥胖症、再生障碍性贫血等疾病[3-4]。生物体内的干细胞位于复杂的细胞微环境中,通过微环境中的细胞因子发生复杂的相互作用以调控细胞的增殖分化等动力学行为,同时每个细胞都表现出分子状态的复杂性和异质性,对微环境信号产生不同的反应。组织器官的干细胞增殖分化动力学形成复杂的动态系统。如何对这样一个复杂系统进行定量研究并建立细胞异常增殖过程的宏观描述是定量生物学研究具有挑战的问题[5-7]。
恶性肿瘤是一类细胞异常增殖的疾病,其发生发展过程伴随着细胞增殖过程的失调、细胞微环境的变化和细胞内的表观遗传变化和基因组变化等。由于实验条件的限制和肿瘤演变过程的长期性和隐匿性。通过实验手段研究肿瘤发生发展过程还面临巨大挑战。对细胞异常增殖过程建立定量描述对于理解肿瘤演变动力学有重要意义。
在肿瘤演变的过程中,肿瘤细胞的异质性和可塑性是对这一动态过程进行定量描述所面临的重要困难。细胞的异质性主要表现为不同细胞的表观遗传性态多样性和随机发生的基因组变化[8-9]。表观遗传或者基因组的异质性都会影响细胞的增殖动力学,表现出细胞动力学型的异质性[10]。由于细胞内在的异质性和细胞内分子相互作用的随机性,细胞在增殖过程中通常会表现出由细胞内在微观状态变化引起的动力学参数的变化,也就是细胞的可塑性。细胞的可塑性在应对微环境变化时具有重要作用,可以使细胞具有更好的适应性,并且在微环境发生变化时提高其存活率[11-12]。而在细胞分裂的过程中,母细胞基因组中的表观遗传修饰需要重构并重新分配给两个子细胞。在这个过程中子细胞对母细胞表观遗传修饰的继承是随机的和不完全的,因此会导致由细胞增殖过程引起的细胞可塑性和异质性[13-15]。细胞可塑性通常与表观遗传修饰相关,在肿瘤治疗过程中通过靶向表观遗传调控因子以逆转肿瘤细胞的增殖动力学一直是备受关注的治疗策略[16-18]。
在肿瘤演变过程中,由于微环境变化和基因组不稳定性等原因,肿瘤细胞的异质性增加,肿瘤细胞基因表达的无序性增加,表现出相对于正常细胞转录水平的熵增加过程[19]。在肿瘤的发生发展过程中,肿瘤细胞之间的差异性随着微环境变化和治疗进程发生变化。在这个过程中,系统的复杂度是如何变化的?特别是肿瘤发生的过程是否是熵增加的过程?在肿瘤治疗过程中伴随恶性肿瘤细胞的死亡和正常细胞的增加,这个过程的熵变化与肿瘤发生过程是相反的吗?对肿瘤发生发展过程中系统状态的定量描述有助于人们对这些问题的理解。
本文根据关于异质性干细胞增殖动力学的数学模型框架[10-20],建立包含细胞增殖分化指标异质性和细胞异常增殖性指标异质性的干细胞增殖模型,通过引进细胞增殖水平对微环境的依赖性,研究微环境变化引起的细胞异常增殖动力学过程。通过对模型模拟的增殖动力学的分析研究细胞异常增殖过程中系统的熵变化,根据熵与细胞数量变化的关系研究不同微环境和调控关系对增殖过程的影响。
1 模型 1.1 异质性干细胞增殖分化模型本文所建立的异质性干细胞增殖模型如图 1所示。该模型的基本结构参考经典的G0期细胞增殖模型[21-22]。在该模型中,具有增殖分化能力的干细胞可以处于静息期(G0期)或细胞分裂期(G1-S-G2-M期)。处于静息期的细胞可以以速率κ分化为下游细胞,或者以速率β进入细胞分裂期。进入细胞分裂期的细胞依次经过细胞分裂前的准备(G1),DNA复制(S),蛋白质合成(G2),和有丝分裂(M),最后分裂成为两个子细胞。处于分裂阶段的细胞可以以一定的速率μ发生细胞凋亡而离开细胞增殖过程。细胞分裂的过程通常需要一定的时间τ。

|
图 1 异质性干细胞增殖分化模型 Figure 1 Heterogeneous stem cell proliferation and differentiation model |
上述的G0期细胞周期模型描述了一般的干细胞增殖过程。为了考虑细胞的异质性,这里引进表示细胞表观遗传态的变量x=(x1, x2),分别以x1表示细胞的增殖分化水平异质性,和以x2表示细胞的异常增殖性指标异质性。通常,细胞的表观遗传态可以包含描述细胞状态的高维向量。在这里主要关心细胞的增殖分化情况,而且主要考虑由于微环境变化引起的细胞异常增殖过程,即与细胞增殖分化能力有关的量化指标,和表示在肿瘤发生过程中的恶性肿瘤细胞异常增殖能力的宏观指标。
细胞的增殖分化能力通常与细胞的干性水平有关,而细胞的干性通常跟多个干细胞特异表达基因的表达有关。近年来有研究工作通过机器学习方法建立细胞基因组转录水平与细胞干性的定量关系[23]。这里没有在基因水平考虑每个基因的表达,而是以一个宏观指标来描述细胞的增殖分化能力。而且还需注意的是,这里的增殖分化指标并不完全等同于干性。因为许多具有增殖分化能力的细胞并不等同于生物学意义上干细胞,例如干细胞分化以后具有快速扩增能力的前体细胞。而对于描述细胞的异常增殖性指标,可以通过基于单细胞RNA测序数据定义的单细胞熵来量化表示细胞的恶性程度[19]。研究表明恶性肿瘤细胞的单细胞熵通常表现出比正常细胞更高的值,表示其对应的基因转录水平相对于正常组织细胞具有更高的无序性。
通过引进细胞的异质性指标x,每个细胞的动力学参数β, κ, μ, τ都依赖于该细胞的指标值x,表现出动力学的异质性。此外,增殖率β还依赖于微环境中的细胞数量N。因此,可以把每个细胞所对应的动力学参数记为增殖率β(N, x),分化率κ(x),凋亡率μ(x),和细胞周期时间τ(x)。这些量构成了每个细胞的增殖动力学特征,也称为是细胞的动力学型(Kinetotype)[10]。
在每次有丝分裂时,每个细胞分裂产生两个子细胞,子细胞的表观遗传状态与相应母细胞的状态并不完全一致。为了描述伴随细胞分裂过程的细胞状态变化,这里引进细胞状态继承函数p(x, y),表示给定母细胞的状态为y的条件下,通过细胞分裂产生一个状态为x的子细胞的概率,也即条件概率:
| $ p(x, y)=P(子细胞状态=x|母细胞状态=y). $ |
需要注意的是,每个细胞的状态在细胞周期过程也会发生变化。在这里忽略这个变化,而以变量x表示细胞周期内的平均状态,因此所对应的细胞动力学型也可以认为是细胞周期内的动力学型参数的平均值。
为了考虑微环境对干细胞增殖分化过程的影响,在模型中加入微环境指标u, 并且假设细胞的异常增殖性指标x2和适应性(凋亡率μ)都依赖于微环境因素。在这里,微环境指标可以表示为细胞所处的环境偏离正常环境的程度,微环境指标越大代表细胞所处的环境越差,越不利于正常细胞的生长。
通过上面所建立的模型,考虑多细胞系统
| $ \Sigma(t)=\left\{x^1(t), x^2(t), \cdots, x^{N(t)}(t)\right\} $ |
这里的细胞数量N(t) 和系统中每个细胞的表观遗传状态xi(t) 都是随时间变化的,同时每个细胞的动力学型也是随着细胞状态的变化而改变。通过模拟每个细胞的动力学行为及其在细胞分裂过程中的细胞状态变化,就可以模拟该多细胞体系的动态变化过程。计算模拟流程参考附录A。
下面给出模型中各项的数学表达式。
1.2 数学表达式 1.2.1 增殖率与分化率在模型中,假设细胞增殖率和分化率都依赖于增殖分化指标x1,并且假设增殖分化指标x1的取值范围为[0, 1],取值越大表示越倾向于细胞干性,而取值越小则越趋向于下游分化的能力。当x1的取值比较大时,细胞倾向于静息态干细胞,表现为比较小但不为零的细胞增殖能力,而分化能力极低;当x1取中间值时,表现为具有快速扩增能力的前体细胞,具有较高的增殖能力,分化能力较低;当x1比较小时,细胞的增殖能力降低,分化为下游细胞的能力增高。根据这一假设,增殖率β和分化率κ对增殖分化指标x1的依赖性的定量关系如图 2(a)所示。

|
图 2 模型函数的图像 Figure 2 Plots of model formulations 注:(a) 增殖率、分化率与增殖分化指标x1关系图,由公式(1)、公式(2)得到;(b) θ与恶性增殖性指标x2之间关系;(c) 适应性函数g(u, x2) 对恶性增殖性指标x2的依赖关系,每条曲线代表不同的微环境指标u取值;(d) 死亡率与适应性函数的关系;(e) 条件期望函数ϕ1(y1);(f) 条件期望函数ϕ2(y2),两条曲线分别表示不同的微环境指标u; 参数取值为s0=1, a1=6.8, a2=2.2, a3=3.25, s1=3.5, θ0=300, θ1=1 000, θ2=0.4, s1=8.5, b1=2.1, s3=6, μ0=0.3, c=1, c1=0.055, c2=0.06, d1=1.3, α1=1.2, α2=2.2. |
增殖率可以通过希尔函数依赖于细胞数量Nq[10],表示静息态中的所有细胞通过释放细胞因子到微环境中影响细胞的增殖能力。因此,根据图 2(a)所示的关系, 取增殖率函数为
| $ \beta=\beta_0 \times \frac{1}{1+\left(N_q / \theta\right)^{s_0}} \times \frac{a_1 x_1+\left(a_2 x_1\right)^{s_1}}{1+\left(a_3 x_1\right)^{s_1}} $ | (1) |
其中,β0表示最大增殖率,Nq表示处于细胞分裂静息期的细胞总数量, θ表示环境中细胞因子对细胞增殖抑制作用的调控系数,与细胞的恶性增殖性指标有关,参数a1, a2, a3主要用于调节增殖率对x1的依赖关系。细胞恶性增殖性指标的增加使得细胞可以减弱环境中细胞因子对细胞增殖的抑制能力,因此增加θ函数的取值。这里设θ与x2满足单调增加的希尔函数关系:
| $ \theta=\theta_0+\theta_1 \frac{x_2^{s_2}}{\theta_2^{s_2}+x_2^{s_2}} $ |
其中θ0, θ1, θ2都是参数。函数θ(x2) 的图像如图 2(b)所示。
类似地,以希尔函数表示分化率对x1的依赖关系,表示为
| $ \kappa=\frac{\kappa_0}{1+\left(b_1 x_1\right)^{s_3}} $ | (2) |
这里κ0为最大分化率,b1为定义分化率的参数。
1.2.2 死亡率与适应性函数为了定量描述细胞对微环境的适应性和细胞的死亡率,首先引入微环境参数u(0 < u < 1) 表示细胞生长微环境的变化,通过适应性函数g(u, x2) 表示具有不同恶性增殖性指标的细胞在不同微环境条件下的适应性。根据假设,u值比较小时代表正常的微环境,此时恶性增殖性指标比较低的细胞具有更高的适应性,而取值较大的u表示异常环境,恶性增殖性指标较大的细胞具有更高的适应性。同时,为了避免极端的边界情况,假设当x2=0或x2=1时对应的适应性为0。根据这些假设,可以唯象地取适应性函数为
| $ g\left(u, x_2\right)=3.0 x_2^u\left(1-x_2\right)^{1-u}, $ |
相应的函数图像如图 2(c)所示。由图 2可以看到。当u比较小时,适应性的极大值点位于x2 < 0.5处。而当u取值较大时,极大值点位于区间x2>0.5。
细胞的死亡率依赖于细胞对环境的适应性。细胞对环境的适应性越好,适应性函数取值越大,则细胞的死亡率越低。因此,死亡率是适应性函数的减函数,在这里取为逻辑斯蒂函数:
| $ \mu=\frac{\mu_0}{1+c e^{g\left(u, x_2\right)}} $ | (3) |
其中μ0, c为常数,并且当适应性g=0时有最大死亡率μ0/(1+c),对应的函数图像如图 2(d)所示。
1.2.3 细胞状态继承函数细胞状态继承函数p(x; y) 通常与细胞周期过程有关,涉及复杂的生物过程,目前还无法通过计算模型模拟这个过程,并且也无法从实验上获取数据对这个函数进行推断。因此,只能通过一般性的关系建立函数的唯象表达式。在这里,主要参考已有的函数形式[10],并根据所引进指标的含义给出相应的细胞状态继承函数。
当状态为y=(y1, y2) 的细胞进行有丝分裂以后,分裂为两个细胞,每个子细胞的属性分别为x1=(x11, x21) 和x2=(x12, x22)。不妨假设两个子细胞x1和x2是对称的,满足相同的条件概率分布, 并且两个指标的继承关系是相互独立的。则可以把继承函数表示为
| $ p(x, y)=p_1\left(x_1 ; y\right) \times p_2\left(x_2 ; y\right), $ |
其中pi(xi; y) 为条件贝塔分布的概率密度函数
| $ p\left(x_i ; y\right)=\frac{x_i^{a_i(y)-1}\left(1-x_i\right)^{b_i(y)-1}}{B\left(a_i(y, ) b_i(y)\right)}, B(a, b)=\frac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)}, $ |
这里Γ(z) 为伽马函数, ai(y) 和bi(y) 为贝塔分布的形状参数。在这里采用贝塔分布主要考虑到细胞的状态指标x1,x2的取值范围都是[0, 1], 而选择不同形状参数的贝塔分布概率密度函数可以表示定义在[0, 1] 内不同形状的条件概率函数形式。
为了选择合适的形状参数函数ai(y) 和bi(y), 首先引进非负函数ϕi(y) 和ηi(y) 使得给定母细胞状态y下的子细胞状态的期望和方差可以表示为
| $ \begin{aligned} & E\left(x_i \mid y\right)=\phi_i(y), \\ & {Var}\left(x_i \mid y\right)=\frac{1}{1+\eta_i(y)} \phi_i(y)\left(1-\phi_i(y)\right), \end{aligned} $ |
则有关系
ai(y)=ηi(y)ϕi(y), bi(y)=ηi(y)(1-ϕi(y)). 在模型计算中,通常取η1(y)=η2(y)=η为常数。为了定义条件期望函数ϕi(y),根据细胞状态指标ϕi(y) 的含义,假设子细胞增殖分化指标的条件期望只依赖于母细胞的增殖分化指标(ϕ1(y)=ϕ1(y1),而子细胞的恶性增殖指标只依赖于母细胞的恶性增殖指标(ϕ2(y)=ϕ2(y2))。考虑到细胞分裂过程中的细胞状态惯性,函数ϕi通常为单调增函数,可以取为希尔函数的形式:
| $ \phi_1\left(y_1\right)=c_1+d_1 \times \frac{\left(\alpha_1 y_1\right)^{1.5}}{1+\left(\alpha_1 y_1\right)^{1.5}} $ | (4) |
| $ \phi_2\left(y_2\right)=c_2+d_2 \times \frac{\left(\alpha_2 y_2\right)^{2.1}}{1+\left(\alpha_2 y_2\right)^{2.1}} $ | (5) |
在这里,c1, c2, d1为常数。假设参数d2按下面的关系依赖于环境指标u:
| $ d_2=0.68 u+0.35, $ |
表示当环境由正常变为异常环境时,会诱导细胞分裂时倾向于产生恶性增殖性指标更高的细胞,也即表示环境变化诱导的细胞恶性变化。函数ϕ1(y1) 和ϕ2(y2) 的图像如图 2(e)-2(f)所示。
1.3 系统熵根据上面给出的模型和函数进行计算模拟,就可以得到多细胞体系演变的动力学过程,也即t时刻状态为x=(x1, x2) 的细胞数量N(t, x1, x2)。根据细胞数量可以计算出状态为x的细胞所占的比例:
| $ f\left(t, x_1, x_2\right)=N\left(t, x_1, x_2\right) / N(t), $ |
其中
| $ N(t)=\int_0^1 \int_0^1 N\left(t, x_1, x_2\right) d x_1 d x_2 $ |
为细胞的总数。由此,容易求得系统在时刻t的熵
| $ E(t)=-\int_0^1 \int_0^1 f\left(t, x_1, x_2\right) \log f\left(t, x_1, x_2\right) d x_1 d x_2 $ | (6) |
熵值E(t) 给出细胞增殖过程中系统复杂性的动态变化。下面的研究中通过细胞总数量N(t) 和熵E(t) 随时间的变化来研究微环境u变化的情况下系统增殖过程的宏观动力学。
2 结果 2.1 正常环境下的干细胞增殖过程首先考虑正常环境下的细胞增殖过程,为此设置环境指标u=0.1。首先初始化500个细胞,每个细胞的增殖分化指标x1在区间[0, 1] 内均匀取值,而恶性增殖性指标x2取不同的值,分别取值于区间[0, 0.1],[0.5, 1],和[0, 1] 三种情况(图 3(a)-(c))。分别对不同的初始条件进行模拟,可以看到在不同初始条件下细胞数量增加的动力学是相同的,表现出类似于逻辑斯蒂增长曲线的过程(图 3(d))。而相应的系统熵变化除开始增殖的最初阶段以外,也迅速收敛于相同的衰减趋势(图 3(e))。在图 3(f)中给出在细胞增殖过程中系统的熵对细胞数量的关系。可以看到对于从不同的初始条件出发,在细胞数量比较少的时候(N < 5 000),初始细胞状态的分布对熵与细胞数量的依赖关系有影响,而当细胞数量比较大时,这一关系趋向于平稳,而与初始条件无关。综合上面结果,在正常环境下,系统从不同初始细胞分布出发都可以收敛到相同的细胞数量和细胞状态的分布,表现出系统平稳态对初始条件的不敏感依赖性。
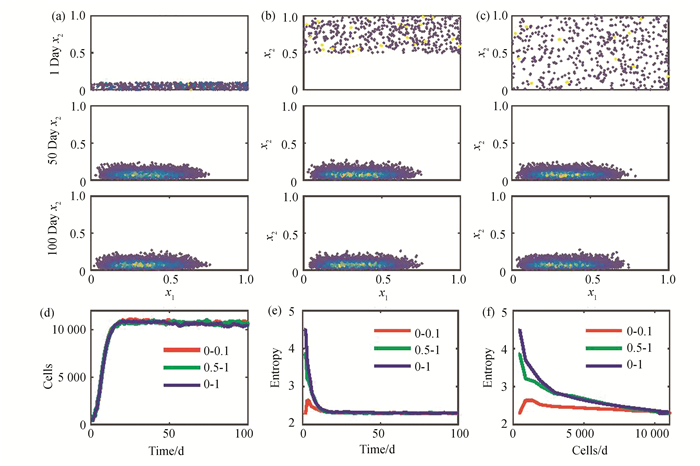
|
图 3 细胞增殖动力学 Figure 3 Stem cell regeneration dynamics 注:(a)-(c) 三种情况下的细胞状态变化散点图;(d) 细胞初始分布不同时系统中细胞数量的变化;(e) 细胞初始分布不同时系统熵随时间的变化情况;(f) 细胞增殖过程的系统熵与细胞数量的关系; 这里β0=15, κ0=0.5, η=70,其他参数如图 2. |
为考虑微环境异常变化情况下的细胞增殖过程,在模型计算中,首先设置u=0.1进行模拟计算到100 d,然后令微环境指标u在100~150 d的时间内增加到异常的环境(u=0.9),然后令u=0.9并继续计算到200 d。根据前面的讨论可以看到,在100 d时系统的状态与初始条件无关。为了比较微环境变化的不同路径对细胞增殖过程的影响,这里选取不同u值的变化路径进行计算(图 4(a))。根据计算结果,在环境指标变化的过程中(100 < t < 150),细胞数量并没有表现出明显的增加。在后面的阶段(t>150),细胞数量快速增加达到新的稳态,表现出宏观的异常增殖动力学(图 4(b))。沿细胞增殖过程,系统的熵在最初的阶段表现出快速上升达到最大值,然后在细胞数量快速增加的阶段系统的熵持续降低(图 4(c))。有趣的是,对于不同的u值变化路径,细胞数量的增殖过程是有区别的,但是熵与细胞数量表现出一致的关系。这一结果显示熵与细胞数量的依赖关系对环境因子变化路径的不敏感依赖性,而可能与系统的参数有关(见后面的讨论)。
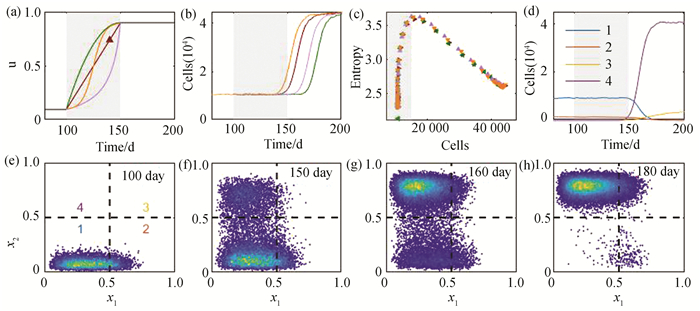
|
图 4 微环境增加诱发的细胞增殖过程 Figure 4 Stem cell regeneration dynamics induced by increasing environmental index 注:(a)环境指标随时间的变化,4条曲线表示不同的变化方式;(b)细胞数量的变化;(c)系统熵与细胞数量的关系,不同的标记对应于(a)中不同的环境指标变化路径;(d)不同表型(由(e)给出)细胞数量的变化;(e)-(h) 不同时间的细胞状态散点图,参数值如图 3. |
由图 4(c)可以看到由于环境变化引起的细胞异常增殖过程并非熵增过程,系统的熵先增加后减小。为了更细致地考察细胞增殖过程,在图 4(e)-4(h)中给出不同时间点细胞状态变化的散点图。通过散点图可以看到,在100 d环境指标还没有开始增加时,细胞主要分布于恶性增殖性指标比较小的正常细胞区域x2 < 0.5 (图 4(e))。而在150 d,细胞数量并没有明显变化,但是已经有大量细胞表现为恶性增殖性指标比较高的异常细胞区域x2>0.5 (图 4(f))。因此,从100~150 d的时间内,细胞的总数量没有明显变化,但是正常细胞数量减少,异常细胞数量增加,表现出环境变化诱导的细胞可塑性。在这个阶段由于细胞的可塑性引起系统熵的增加。而在150 d以后的阶段,正常细胞持续减少,异常细胞数量持续增加,并且具有更高的增殖率,细胞总数量快速增加(图 4(g)-4(h))。在这个阶段,系统趋向于新的由异常细胞主导的平衡状态,系统的熵减少。根据细胞状态x的取值将细胞分为4种表型,分别画出4种表型细胞数量变化的动力学,可以看到后期的细胞数量快速增加主要是由于异常的快速增殖性细胞的数量增加引起的(图 4(d))。
由图 4的结果可以看到微环境指标由正常变为恶性环境时,细胞异常增殖过程表现出显著的分阶段特性。首先是在初期阶段,细胞数量并没有明显改变,但是系统的熵值显著增加,主要表现为系统中的细胞异质性增加,非恶性细胞数量减少,恶性细胞数量增加。然后,在后期阶段表现为细胞数量的快速增加,系统的熵值降低,细胞表型趋向于恶性细胞。这两个阶段的不同特点与癌症发生过程的动力学特征是相符合的。在癌症发生早期,细胞增殖现象并不明显,临床诊断困难,而通常会表现出细胞表型的变化和细胞异质性的增加,例如在许多早期肿瘤样本中可以检测到DNA甲基化的变化和极早期肿瘤细胞等[24-25]。而细胞数量的快速增加通常发生在肿瘤演变的后期。此时特定表型的细胞获得竞争优势,相应的细胞数量快速增加,肿瘤内细胞类型趋向于稳定。
2.3 伴随微环境恢复的细胞增殖过程现在进一步考虑在微环境指标值增加导致细胞异常增殖以后,再使微环境指标恢复正常值时细胞增殖动力学的变化。当环境指标恢复正常以后,有两个问题是最为关心的,一是系统的细胞总数量和细胞表观遗传状态分布是否会恢复正常值,二是如果系统确实可以恢复正常状态,那么恢复过程是否是细胞异常增殖过程的逆过程?
为回答上述问题,在前面计算的基础上,当在200 d环境指标达到u=0.9之后,在200~250 d内以不同的速率将环境指标减少到u=0.1 (分别采取与环境指标增加过程相同函数形式的逆过程)。在250 d以后环境指标维持正常值u=0.1不变。计算表明,随着环境指标的恢复,细胞数量同时恢复到正常水平(图 5(a))。我们还注意到,当环境指标增加时,在150 d, u达到0.9时,细胞数量并没有达到新的稳态,而是需要一个延迟的时间才能达到新的稳态值。而当环境因素恢复时,当在250 d后u恢复为0.1时,细胞数量就都已经恢复到正常值水平,细胞数量的恢复不需时间的延迟。这一结果表明当环境指标增加或者减少时,细胞数量的变化过程并不是完全可逆的。

|
图 5 环境恶化与恢复过程的细胞增殖动力学 Figure 5 Cell regeneration dynamics with microenvironment changes 注:(a) 环境指标的动态变化与相应的细胞数量变化;(b) 伴随环境指标变化过程的系统熵与细胞数量的关系,图中小方块图显示了不同时刻所对应的细胞状态散点图,橙色表示沿环境恶化过程,蓝色表示沿环境恢复过程.(彩图见电子版:http://swxxx, alljournals.cn/ch/index.aspx.2024年第22卷第1期). |
为进一步考察系统恢复过程细胞状态的变化,我们计算系统的熵随恢复过程的变化,并且比较系统的熵与细胞数量的关系。根据不同的微环境变化曲线所对应的计算结果如图 5(b)所示,结果显示随着环境指标先增加后减少恢复正常的过程,系统熵和细胞数量的关系呈现‘ ∞ ’型的变化趋势。特别是在环境指标恢复的过程中,状态恢复过程的变化趋势与异常增殖过程的逆过程不同。当环境指标增加时,系统表现出两阶段的过程,首先是熵值增加而细胞数量基本保持不变,然后是细胞数量快速增加而熵值持续减小。而环境指标恢复过程的动力学分为三个阶段,首先是系统熵的小幅增加。通过图 5(b)中对应的细胞状态散点图,在这一阶段细胞状态由比较集中的恶性增殖状态开始向非恶性状态转变。在第二个阶段中系统熵维持不变,同时细胞数量快速下降。这一阶段中细胞状态开始整体向正常状态转变,有越来越多的细胞变为正常的异常增殖性指标较低的细胞。在最后的阶段系统的熵和细胞数量同时下降到正常水平,此时由于环境指标趋向于正常,异常增殖状态的细胞逐渐死亡,细胞状态逐渐集中于正常增殖状态细胞。最后细胞数量和细胞表观遗传状态的分布都恢复到正常微环境的情况。
上述结果表明,在环境恢复过程中细胞数量和系统熵的变化都并不沿细胞异常增殖过程的逆过程变化。在现实情况下,疾病的恢复过程通常也并不简单地是疾病发生过程的逆过程。这里的计算结果表明系统恢复过程中微观的细胞状态变化和细胞数量的宏观变化是同步发生的,与细胞异常增殖过程中首先发生细胞状态变化然后再发生细胞数量的变化不同。而在恢复过程的最后阶段,虽然细胞数量已经降低到接近正常水平,然而系统熵仍然比较高,表明系统中还有残留恶性细胞。该计算结果提示在肿瘤临床治疗中,通常需要在细胞数量恢复正常以后再巩固治疗一段时间以清除残余肿瘤细胞。
2.4 熵与细胞数量的依赖关系在前面的讨论中可以看到,对于不同的环境指标增加曲线,熵对细胞数量具有很一致的依赖关系(图 4(c))。特别是,当细胞数量快速增加时,熵随细胞数量的增加而减少的趋势是相同的。由此,可以把细胞异常增殖过程中熵对细胞数量的依赖关系表示为函数E(N)。而函数E(N) 与环境指标的变化过程无关,那么是否与系统的参数有关呢?下面来详细讨论这一问题。
2.4.1 对动力学参数β0、κ0、μ0的依赖关系首先考虑动力学参数β0、κ0、μ0对干细胞增殖过程中熵变化的影响。为此,随机选取多组(β0, κ0, μ0) 的参数值,模拟在不同参数组合下细胞异常增殖过程中熵的变化情况。图 6(a)给出了异常增殖过程中熵对细胞数量的依赖关系,每条曲线代表不同的参数组合。根据前面的计算可以看到随着细胞数量的增加,熵值首先增加到最大值,然后单调减小。为了考虑熵值上升和下降阶段的一般规律,首先对细胞数量进行归一化,每条轨道以熵值达到最大值时所对应细胞数量N*作为归一化参数。因此,在图 6(a)中,对不同轨道的熵值最大值都取值于横坐标为1的位置。容易看到,不同的参数所对应的熵变化趋势基本相同。特别地,对于主要关注的细胞数量快速增加过程的熵减少过程,当细胞数量趋向于新的平衡态时,E(N) 都呈下降趋势,可以通过线性函数
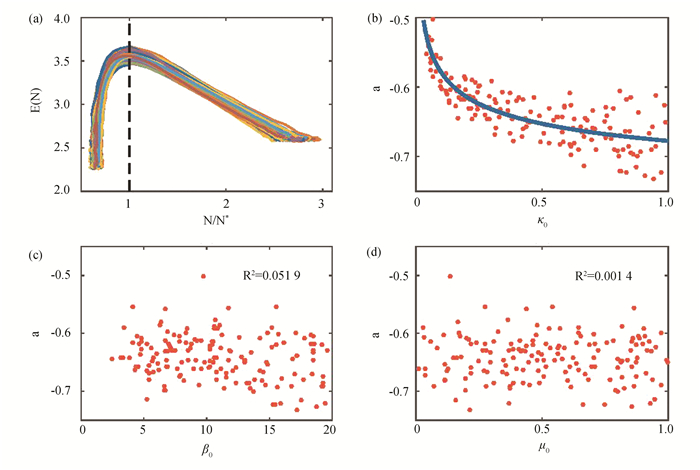
|
图 6 函数E(N)对动力学参数的依赖关系 Figure 6 Dependence of function E(N) and kinetic parameters 注:(a)不同参数组合(β0, κ0, μ0) 下的熵与细胞数量关系,这里N*表示当熵值达到最大时的细胞数量;(b)方程(7)中的系数a与κ0的关系,实线表示拟合结果(8);(c)方程(7)中的系数a与β0的关系; (d)方程(7)中的系数a与μ0的关系. |
| $ E(N)=a\left(N / N^*\right)+E_0 $ | (7) |
进行拟合。因此,为了表示熵-细胞数量关系E(N) 对动力学参数(β0, κ0, μ0) 的依赖,主要考虑斜率a对参数的依赖关系。
通过考察系数a对不同参数的依赖关系,得到系数a是对分化率κ0有明显的非线性相关性,当分化率越低时系数a的值越小(图 6(b))。而系数a对增殖率β0和死亡率μ0的皮尔逊相关性系数R2都比较低,由此认为a对上述两个参数没有明显的依赖关系(图 6(c)-6(d))。因此,可以把系数a表示成依赖于分化率κ0的函数。通过对数据的拟合,可以得到以下近似关系:
| $ a\left(\kappa_0\right)=0.1522 \kappa_0^{-0.2168}-0.8296 $ | (8) |
由(7)-(8)可得到
| $ E(N)=a\left(\kappa_0\right)\left(\frac{N}{N^*}\right)+E_0 $ | (9) |
因此,当分化率κ0越小时,熵下降的趋势越平缓,但不管参数如何变化,最后平衡态时的熵值都相同。
2.4.2 对细胞可塑性参数α1,α2的依赖关系下面来考虑E(N) 对细胞可塑性的依赖关系。据前面的模型介绍,细胞的可塑性主要通过细胞状态的继承函数来描述。而对继承函数的定义中最重要的是定义条件期望函数ϕ1(y1) 和ϕ2(y2)。因此,在这里主要考虑熵变化关系对条件期望函数中的参数α1和α2的依赖性。根据上面的讨论,只需要看函数(7)中的系数a对参数α1和α2的依赖关系。
首先固定α2=2.0,在区间[0.1, 1.5] 内随机选取参数α1,其他参数如图 3给出的缺省参数。按照上面同样的过程计算在微环境指标增加时的细胞异常增殖过程,得到不同参数下细胞数量的变化曲线如图 7(a)所示。可以看到,对于不同的参数α1, 细胞数量的变化趋势相同,但是最后平稳态的细胞数量不同。进一步考察熵对细胞数量的依赖关系,得到类似于前面图 6(a)的结果,也即可以通过关系7进行拟合(图 7(b))。拟合系数a对参数α1的关系由图 7(c)给出,两者不具有明显的依赖性。由图 7(b)还可以注意到,但是对于不同的α1,熵的最大值不同。
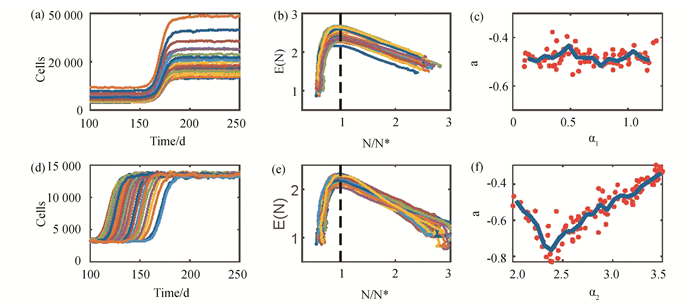
|
图 7 函数E(N)对细胞可塑性参数的依赖关系 Figure 7 Dependence of function E(N) and cell plasticity parameters 注:(a) 不同的参数α1时对应的细胞数量变化;(b) 不同参数α1时熵与细胞数量的关系;(c) 系数a对参数α1的关系,实线表示α1与a的平均值间的关系;(d) 不同的参数α2时对应的细胞数量变化;(e) 不同参数α2时熵与细胞数量的关系;(f) 系数a对参数α2的关系,实线表示α1与a的平均值间的关系; 在(a)-(c) 中, α2=2.0, α1随机取值于[0.1, 1.5];在(d)-(f) 中,α1=0.1, α2随机取值于[2.0, 3.5]. |
然后,固定α1=0.1不变,参数α2随机取值于区间[2.0, 3.5],所得到的结果如图 7(d)-7(f)所示。此时,注意到环境指标u=0.9时的平稳态细胞数量对α2的取值不敏感,但是对于不同的α2,熵的最大值是不相同的,并且系数a表现出对α2的非单调依赖关系。因为E(N) 描述了在给定细胞数量下系统中细胞表观遗传状态分布的宏观状态,由上面结果可以看到,对细胞可塑性调控关系的变化会影响到细胞异常增殖过程中细胞表观遗传状态分布的动态变化。
3 讨论细胞增殖分化是多细胞生命的基本生物学过程,在这个过程中生命组织中宏观的细胞数量和微观的细胞内分子状态都发生变化,是多尺度的复杂动力学过程。细胞增殖分化过程的失调会引发包括癌症在内的许多疾病。在临床诊断中,对宏观状态的检验相对比较容易,而对微观细胞分子状态的检测还面临技术、费用、伦理等多重挑战。因此,如何根据有限的检验信息建立宏观信息和微观信息的关系是在临床诊断和病理分析中所面临的重要问题。目前,单细胞技术的应用使得人们可以在单细胞水平测量分子的组学数据信息,但是这一技术在临床应用中还面临很多困难。特别是这一技术无法在活体中直接进行测量,而只能通过少量样本细胞进行测量。为通过少量样本数据获取整体组织细胞的宏观性质,根据样本数据的分布所定义的系统熵可以作为度量细胞异质性的宏观指标。因此,通过细胞增殖过程的系统熵与细胞数量的依赖关系可以建立宏观信息与微观信息之间的关系。
本文建立了基于细胞增殖分化潜能和恶性增殖程度的异质性干细胞增殖模型,通过模型计算研究由于微环境变化驱动的细胞异常增殖过程,通过对增殖过程的分析研究系统熵和细胞数量的依赖关系。通过模型计算发现当微环境从正常变为异常环境时,系统表现出两阶段的动力学过程,细胞数量在早期变化不大,而在后期快速增加。与之对应,系统熵表现为先增后减的过程。当熵值达到最大值时,不同细胞之间的系统差异性达到最大,系统处于细胞数量快速增加前的临界转变状态。这一结果与近年来所发展的临界点理论相符合[26]。此外,系统熵与细胞数量的关系与环境指标变化的路径无关,主要依赖于细胞增殖率和细胞增殖分裂过程的可塑性变化。因此,有可能通过跟踪细胞增殖过程中熵与细胞数量的变化关系对系统参数,也就是相关的生理指标进行推断。
本文还对微环境指标从恶性环境恢复到正常值的过程进行模拟计算,研究系统状态恢复过程中熵与细胞数量关系的动力学变化。研究表明尽管环境指标变化的过程是严格的逆过程,系统的恢复过程并不是异常增殖过程的逆过程,而是表现出不同的动力学行为。特别地,恢复过程不存在明显的临界转变状态,熵值变化表现出3阶段的特点,分别是熵增、维持和熵减过程,其中中间的熵值维持阶段伴随细胞数量的快速减少。这些结果对生命体中由于环境变化引起的细胞异常增殖和恢复过程提供了定量的描述。
癌症是一类细胞异常增殖的疾病,微环境的变化对于癌症演变和耐药复发过程都具有重要影响。在癌症演变的过程中,随着微环境的变化,正常组织细胞的适应性降低,部分细胞随着环境的变化逐步演变为适应肿瘤微环境的肿瘤细胞,而成为组织中的主要组分。这一演变过程通常伴随细胞数量和细胞表型的变化。本文以一般性的异质性细胞增殖模型研究环境因素变化诱导的细胞异常增殖过程动力学,对癌症演变过程中不同尺度信息之间的关系给出定性的刻画。特别地,通过计算建立细胞增殖过程临界转变状态与熵值最大点的关系,提示在癌症演变的早期有可能细胞数量(肿瘤体积)变化并不明显,但是细胞表型已经发生显著变化。这些研究对于癌症病人的早期诊断和干预具有重要的意义。当然,对本文的内容和结果的临床应用还需要更加深入的研究。
4 结论1) 本文建立异质性干细胞增殖的数学模型,研究当微环境发生变化时的异质性干细胞异常增殖的动力学过程。通过研究发现在由微环境变化导致的干细胞异常增殖过程中系统熵先增加后减小,并且在这一过程中熵的变化与环境变化路径无关,熵变化表现出对环境变化过程的不完全依赖性。在这一异常增殖过程中,细胞的表观遗传状态的分布发生明显变化,表现出向恶性增殖状态过渡直到绝大部分细胞完全恶化的过程。这些结果为定量描述细胞异常增殖过程提供了参考。
2) 随后模拟当环境逐渐恢复正常时细胞数量也会逐渐恢复正常的过程。环境恢复过程中系统熵值的变化呈现出三个阶段,分别是熵增、维持和熵减阶段,表现出与细胞异常增殖过程完全不同的特点。这一过程为刻画细胞异常增殖类疾病的恢复过程提供了参考。
3) 最后,通过考虑模型参数对细胞异常增殖过程的影响,经过大量模拟以及数据拟合,给出了熵变化对不同参数的依赖关系。为今后针对性地研究细胞异常增殖的影响因素提供了思路。
附录 计算模拟过程在对系统的计算模拟中,采用基于个体模型,模拟每个细胞的状态变化。模拟程序包括系统模块和单细胞模块。系统模块主要用于设置模型参数和更新细胞数量,细胞模块包含各种细胞属性和参数变化。系统中细胞数量随着时间动态变化。计算模拟过程如下:
1) 初始化
① 系统初始化:设置初始细胞数量N=N0;初始化系统环境指标u。
② 细胞初始化:对N0个初始细胞,初始化每个细胞的增殖分化指标值x1和异常增殖性指标值x2。初始化细胞状态S=0,表示所有细胞的初始状态都为静息态,并设置增殖时间a=0。令静息期细胞数量Nq=N0,分裂期细胞数量Np=0。
2) 迭代计算
设置初始时间t0, 时间步长Δt, 和终止时间T。
① 细胞命运决定:遍历系统中的所有细胞,对每个细胞决定细胞下一步的命运:
a) 对静息态细胞,计算相应的增殖率β和分化率κ,并按照增殖概率βΔt和分化κΔt决定该细胞在下一步是增殖、分化还是保持不变。
b) 对增殖态细胞,判断细胞增殖时间a是否大于τ。如果是,则在下一步进入细胞分裂状态;如果不是,则或以概率μΔt死亡,或维持细胞增殖状态不变。
② 系统状态更新:遍历所有细胞,对每个细胞按照其细胞命运进行状态更新:
a) 如果细胞命运是分化或者死亡,则把细胞移除,并令总细胞数量减1,N=N-1,相应地,根据细胞在静息期还是分裂期,令Nq=Nq-1或Np=Np-1。
b) 如果细胞命运是从静息态变为增殖态,则设置细胞状态为增殖态(S=1),并设置细胞增殖时间a=0,令Nq=Nq-1, Np=Np+1,细胞总数量N不变。
c) 如果细胞命运是维持增殖状态不变,则增加细胞增殖时间,a=a+Δt,细胞数量Nq,Np和N不变。
d) 如果细胞命运是分裂,则变为两个子细胞,每个子细胞的状态按照细胞状态继承函数进行设定,并设置每个子细胞的增殖时间a=0,细胞总数量增加1,令Nq=Nq+2,Np=Np-1, N=N+1。
e) 更新时间t=t+Δt,并更新环境指标值u。
3) 如果t>T,停止计算,否则,重复2步迭代计算
上面的计算过程给出了模型模拟的基本过程。另外,在计算过程中还有一个细节需要考虑。因为在模拟过程中细胞数量会指数增加,在模拟大量细胞时,有可能会发生计算机内存不足的问题。为此,可以设置最大可计算的细胞数量MaxNumCell,当细胞数量超过最大容纳量时,只选取部分细胞进行下一步计算,同时以变量fprolif记录细胞数量的增长因子。在选择进入下一步计算的细胞时,通常对处于增殖态的细胞需要全部选取,而仅对处于静息态的细胞按比例
| $ f=\min \left\{1, \frac{\text { MaxNumCell-增殖态细胞数量 }}{\text { 静息态细胞数量 }}\right\}, $ |
进行随机选取,使得用于计算的总细胞数量小于最大可容纳量MaxNumCell。在这里不淘汰增殖态的细胞,是因为增殖态的细胞正在完成增殖过程,在这一过程完成以前不能被淘汰,否则就会导致细胞数量的意外丢失。
| [1] |
ALVARADO A S, YAMANAKA S. Rethinking differentiation: stem cells, regeneration, and plasticity[J]. Cell, 2014, 157(1): 110-119. DOI:10.1016/j.cell.2014.02.041 (  0) 0) |
| [2] |
FUCHS E, TUMBAR T, GUASCH G. Socializing with the neighbors: stem cells and their niche[J]. Cell, 2004, 116(6): 769-778. DOI:10.1016/s0092-8674(04)00255-7 (  0) 0) |
| [3] |
LI L H, CLEVERS H. Coexistence of quiescent and active adult stem cell in mammals[J]. Science, 2010, 327(5965): 542-545. DOI:10.1126/science.1180794 (  0) 0) |
| [4] |
METHAROM P, DOYLE B, CAPLICE N M. Clinical trials in stem cell therapy: pitfalls and lessons from the future[J]. Nature Reviews Cardiology, 2007, 4(Suppl 1): S96-S99. DOI:10.1038/ncpcardio0730 (  0) 0) |
| [5] |
STIEHI T, MARCINIAK-CZOCHRA A. Stem cell self-renewal in regeneration and cancer: insights from mathematical modeling[J]. Current Opinion in Plant Biology, 2017, 5: 112-120. DOI:10.1016/j.coisb.2017.09.006 (  0) 0) |
| [6] |
MACARTHUR B D. Collective dynamics of stem cell populations[J]. Proceedings of the National Academy of Sciences of the USA, 2014, 111(10): 3653-3654. DOI:10.1073/pnas.1401030111 (  0) 0) |
| [7] |
FURUSAWA C, KANEKO K. A dynamical-systems view of stem cell biology[J]. Science, 2012, 338: 215-217. DOI:10.1126/science.1224311 (  0) 0) |
| [8] |
DAGOGO-JACK I, SHAW A T. Tumour heterogeneity and resistance to cancer therapies[J]. Nature Reviews Clinical Oncology, 2018, 15: 81-94. DOI:10.1038/nrclinonc.2017.166 (  0) 0) |
| [9] |
PRASETYANTY P R, MEDEMA J P. Intro-tumor heterogeneity from a cancer stem cell perspective[J]. Molecular Cancer, 2017, 16(41): 1-9. DOI:10.1186/s12943-017-0600-4 (  0) 0) |
| [10] |
LEI Jinzhi. A general mathematical framework for understanding the behavior of heterogeneous stem cell regeneration[J]. Journal of Theoretical Biology, 2020, 492: 110196-1. DOI:10.1016/j.jtbi.2020.110196 (  0) 0) |
| [11] |
AHMED F, HAASS N. Microenviroment-driven dynamic heterogeneity and phenotypic plasticity and phenotypic plasticity as a mechanism of melanoma therapy resistance[J]. Frontiers in Oncology, 2018, 8: 173. DOI:10.3389/fonc.2018.00173 (  0) 0) |
| [12] |
FLAVAHAN W A, GASKELL E, Bernstein B E. Epigenetic plasticity and the hallmarks of cancer[J]. Science, 2017, 357(6348): 266. DOI:10.1126/science.aal2380 (  0) 0) |
| [13] |
ZHANG Hang, TIAN Xiaojun, MUKHOPADHYAY A, et al. Statistical mechanics model for the dynamics of collective epigenetic histone modification[J]. Physical Review Letters, 2014, 112(6): 068101. DOI:10.1103/physrevlett.112.068101 (  0) 0) |
| [14] |
CORTINI R, BARBI M, CARÈ B, et al. The physics of epigenetics[J]. American Physical Society, 2016, 88: 025002. DOI:10.1103/RevModPhys.88.025002 (  0) 0) |
| [15] |
HUANG R, LEI J. Dynamics of gene expression with positive feedback to histone modifications at bivalent domains[J]. International Journal of Modern Physics B, 2018, 32(7): 1850075-1. DOI:10.1142/S0217979218500753 (  0) 0) |
| [16] |
FIELD A E, ROBERTSON N A, WANG T, et al. DNA methylation clocks in aging: categories, causes, and consequences[J]. Molecular Cell, 2018, 71(6): 882-895. DOI:10.1016/j.molcel.2018.08.008 (  0) 0) |
| [17] |
CHANG H H, HEMBERG M, BARAHONA M, et al. Transcriptome-wide noise controls lineage choice in mammalian progenitor cells[J]. Nature, 2008, 453(7194): 544-547. DOI:10.1038/nature06965 (  0) 0) |
| [18] |
DAWSON M, KOUZARIDES T. Cancer epigenetics: From mechanism to therapy[J]. Cell, 2012, 150(1): 12-27. DOI:10.1016/j.cell.2012.06.013 (  0) 0) |
| [19] |
LIU Jingxin, SONG You, LEI Jinzhi. Single-cell entropy to quantify the cellular order parameter from single-cell RNA-seq data[J]. Biophysical Reviews and Letters, 2020, 15(1): 35-49. DOI:10.1142/S1793048020500010 (  0) 0) |
| [20] |
LEI Jinzhi. Evolutionary dynamics of cancer: From epigenetic regulation to cell population dynamics-mathematical model framework, application, and open problems[J]. Science China Mathematics, 2020, 63: 411-424. DOI:10.1007/s11425-019-1629-7 (  0) 0) |
| [21] |
BUANS F J, TANNOCK I F. On the existence of G0-phase in the cell cycle[J]. Cell Proliferation, 2010, 3(4): 321-334. DOI:10.1111/j.1365-2184.1970.tb00340.x (  0) 0) |
| [22] |
LEI J, LEVIN S, NIE Q. Mathematical model of adult stem cell regeneration with cross-talk between genetic and epigenetic regulation[J]. Proceedings of the National Academy of Sciences of the USA, 2014, 111(10): 880-887. DOI:10.1073/pnas.1324267111 (  0) 0) |
| [23] |
MAITA T M, SOKOLOV A, Gentles A J, et al. Machine learning identifies stemness features associated with oncogenic dedifferentiation[J]. Cell, 2018, 173(2): 338-354. DOI:10.1016/j.cell.2018.03.034 (  0) 0) |
| [24] |
YANG X, GAO L, ZHANG S. Comparative pan-cancer DNA methylation analysis reveals cancer common and specific patterns[J]. Brief Bioinformatics, 2017, 18(5): 761-773. DOI:10.1093/bib/bbw063 (  0) 0) |
| [25] |
ZHANG P, YANG M, ZHANG Y, et al. Dissecting the single-cell transcriptome network underlying gastric premalignant lesions and early gastric cancer[J]. Cell Reports, 2019, 27(6): 1934-1947. DOI:10.1016/j.celrep.2019.04.052 (  0) 0) |
| [26] |
LIU R, WANG X, AIHARA K, et al. Early diagnosis of complex diseases by molecular biomakers, network biomarkers, and dynamical network biomarkers[J]. Medicinal Research Reviews, 2014, 34(3): 455-478. DOI:10.1002/med.21293 (  0) 0) |
 2024, Vol. 22
2024, Vol. 22


