遗传信息的传递和获取是通过核小体的定位来实现的,仅相隔几个bp就可能对基因表达产生重大的影响。因此,染色体的基本单元——核小体[1],是影响表观遗传状态的主要因素。核小体的定位对基因的表达调控有重要的影响,它的定位变化总是伴随着基因从抑制到转录状态的转变。大量实验结果表明,核小体的形成和在染色质的精准定位是真核生物基因表达所必需的。有人提出核小体的形成及其在染色质上的精准定位有以下两方面的作用:(1)提供一个支架结构,使转录因子之间的信息传递更有效;(2)染色质结构的不均一性,即某些区域不形成核小体,保证了转录因子易于接近染色质模板。经研究表明真核生物基因转录起始区域的核小体定位分布具有高度保守性[2-3],任何真核生物其核小体在基因转录区和编码区的定位图谱上总体都呈现一种周期性振荡衰减趋势[4-5]。但进一步观察后会发现:在细节上,不同物种的核小体占位图谱是有明显差别的,这种差异性可能代表了物种在染色质结构和功能上的进化印迹[6]。但是目前,对于核小体定位预测和定位性质的分析大多数为定性分析,单细胞生物和多细胞生物核小体在结构上的差异性仍然不明确[7-8],影响了我们对基因组的认识进程。因此,如何定量获取核小体定位分布的空间尺度特征和频谱特征尤为迫切。
利用传统的频谱分析方法——快速傅里叶变换(FFT)获得了分布模型的功率谱和相位谱,并在此基础上对酵母和果蝇两种模式生物的频谱特征进行了比较和分析[9]。但傅里叶变换存在的问题是:(1)没有时间-频率的定位功能;(2)不能获得瞬时频率;(3)傅里叶变换在时间和频率分辨率上具有局限性。尽管通过快速傅里叶变换得到了初步的核小体定位信号的频谱特征,但想要进一步研究核小体组织结构,必须要有一种具有自适应性的高分辨率频谱分析方法的介入。
希尔伯特-黄变换(HHT)的独特之处在于分析信号过程中不需要基函数,其由两部分组成:经验模式分解(EMD)[10-11]和Hilbert谱分析。首先,采用EMD方法将定位信号序列分解为一组本征模态函数,再通过希尔伯特变换可得到具有明显物理意义的参量:瞬时频率谱和边际谱。其次,本文通过加入类型强度不同的白噪声改善希尔伯特-黄变换存在的模态混叠。通过改进的希尔伯特-黄变换定量的提取核小体定位信号的特征,从而明确单细胞生物和多细胞生物核小体在结构上的差异性,加快我们对基因组的认识进程。
1 希尔伯特-黄变换 1.1 数据来源研究的主要目的是比较单细胞生物和多细胞生物在核小体组织结构上的差异性,同时又要考虑其可比较性。由于哺乳动物细胞已分化,在选择分化时期的标准上比较困难,所以选择果蝇胚胎期细胞,既具有单细胞的典型特征又具有多细胞分化过渡的特征,满足需要的可比较性。
选取的两个实验数据其实验精度和分辨率均已达到实验要求。
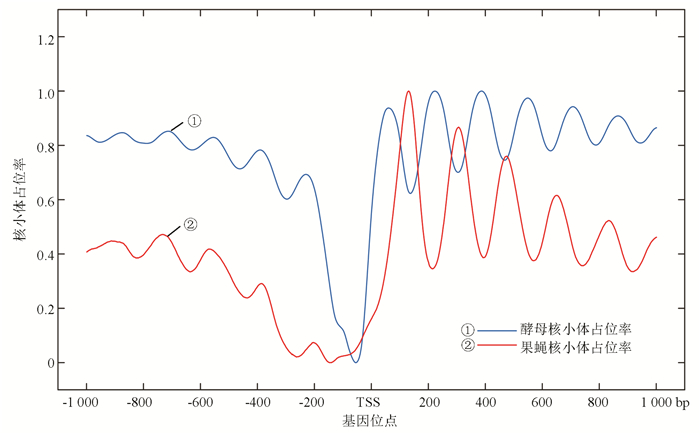
综上考虑,选择来源于William Lee[12]等人于2007年发布的高分辨率酵母核小体定位率实验数据和来自于2008年Travis N. Mavrich[13]等人获得的果蝇胚胎期核小体定位实验数据(见图 1)。
|
图 1 两种模式生物核小体定位图谱 Figure 1 Nucleosome occupancy map of two model organisms |
Wu和Huang提出的希尔伯特-黄变换(HHT)主要分为两步:经验模态分解与希尔伯特变换。经验模式分解(EMD)主要用于将非线性和非平稳信号分解为一系列本征模态函数(IMF)。将通过EMD分解的IMF进行Hilbert变换可以得到具有实际物理意义的瞬时频率。
以实信号ci(t)为例对Hilbert进行介绍,假设实信号x(t)的希尔伯特变换为
| $ {{\hat{c}}_{i}}\left( t \right)=H\left[ c\left( t \right) \right]=\frac{1}{\mathit{\pi }}P\int_{-\infty }^{\infty }{\frac{c\left( \tau \right)}{t-\tau }\text{d}\tau } $ | (1) |
其中P表示柯西(Cauchy)主值。根据这个定义,ci(t)和
| $ {{z}_{i}}\left( t \right)={{c}_{i}}\left( t \right)+j{{{\hat{c}}}_{i}}\left( t \right)={{a}_{i}}\left( t \right)\cdot {{\text{e}}^{\text{j}{{\theta }_{i}}\left( t \right)}} $ | (2) |
其中:
| $ \begin{align} & {{a}_{i}}\left( t \right)=\sqrt{c_{i}^{2}\left( t \right)+\hat{c}_{i}^{2}\left( t \right)}, \\ & \ \ \ {{\theta }_{i}}\left( t \right)=\arctan \left( \frac{{{{\hat{c}}}_{i}}\left( t \right)}{{{c}_{i}}\left( t \right)} \right) \\ \end{align} $ | (3) |
其中ai(t)是ci(t)的瞬时幅度,它可以反映ci(t)的能量随时间变化,θi(t)是ci(t)的瞬时相位。很容易获得相位,每个IMF的瞬时频率可以通过相位的导数来定义,如公式(4)所示:
| $ {{\omega }_{i}}\left( t \right)=\frac{\text{d}{{\theta }_{i}}\left( t \right)}{\text{d}t} $ | (4) |
我们可以用以下形式表示数据x(t),其不包含残留物rn(t)
| $ x\left( t \right)=\operatorname{Re}\sum\limits_{i=1}^{n}{{{a}_{i}}\left( t \right)\cdot {{\text{e}}^{\text{j}\int{{{\omega }_{i}}\left( t \right)\text{d}t}}}} $ | (5) |
H(ω, t)定义为希尔伯特振幅谱:
| $ H\left( \omega , t \right)=\operatorname{Re}\sum\limits_{i=1}^{n}{{{a}_{i}}\left( t \right)\cdot {{\text{e}}^{\text{j}\int{{{\omega }_{i}}\left( t \right)\text{d}t}}}} $ | (6) |
通过定义希尔伯特振幅谱,经验模态分解得到的本征模态函数进行希尔伯特变换即可获得时频分析中两个重要的参量:瞬时频率与瞬时幅度谱。黄锷博士在此基础上引进两个新的物理参量:边际谱h(ω)与瞬时能量密度级IE:
| $ h\left( \omega \right)=\int_{0}^{T}{H\left( \omega , t \right)\text{d}t} $ | (7) |
| $ \text{IE}=\int_{\omega }{{{H}^{2}}\left( \omega , t \right)\text{d}\omega } $ | (8) |
通过以上计算式可以得出将原始信号做Hilbert变换就是原始信号与信号
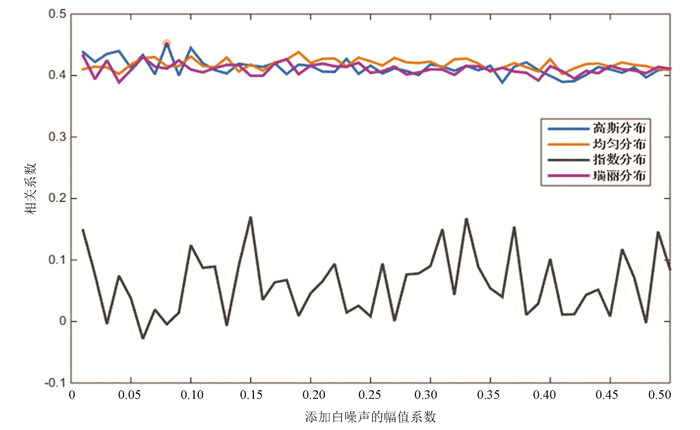
当信号中包含有间歇性成分时,EMD算法易产生模态混叠现象[14]。为了解决模态混叠,黄等人对EMD进行了一些重要的改进,提出了集合经验模式分解(EEMD)[15],EEMD可以通过分解包含不连续信号的混合信号来消除模式混合,应用相位-幅度耦合方法来量化高频带和低频带之间的相互作用,利用分析独立成份消除模式混合,改善每个IMF的正交性,但是它具有幅度和序列不确定性的局限性。因此在酵母和果蝇定位信号中分别加入高斯分布、均匀分布、指数分布和瑞利分布的白噪声,通过调节所加白噪声的幅值系数(信噪比)观察分解结果,以获得最佳标准差下模态混叠最小的白噪声参数(见图 2),然后计算每一个IMF和剩余量分量(Residual)与原始信号的皮尔逊相关系数,平均后得出模态混叠判定指标ρ。
|
图 2 加入四种白噪声后的相关系数曲线(酵母) Figure 2 Correlation coefficients of four white noise distributions(Yeast) |
由图 2可知,酵母核小体定位谱在加入幅值系数为0.08的高斯分布白噪声后,分解得到的IMF整体与原始信号相关性最大,分解效果最好;加入指数分布白噪声后,分解分解得到的IMF整体与原始信号相关性最小,分解效果最差。
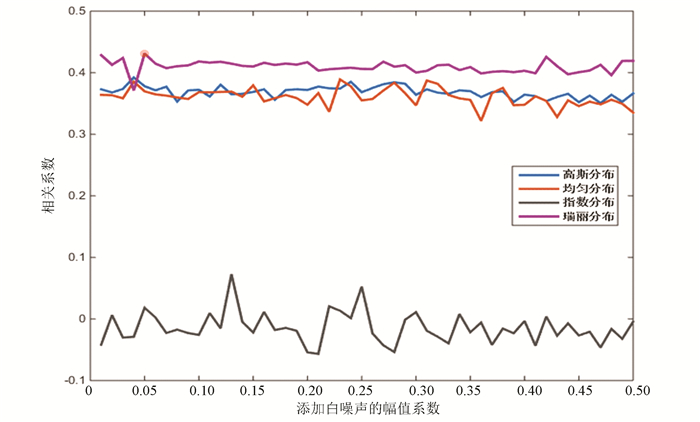
对比图 2与图 3,果蝇核小体定位分布谱同样是在添加指数分布白噪声时分解效果最差,但当加入幅值系数为0.06的瑞丽分布白噪声时,IMF整体与原始信号的相关性最高,效果最好。
|
图 3 四种白噪声分布下相关性对比(果蝇) Figure 3 Correlation comparison of four white noise distributions (Drosophila) |
为了便于描述,将添加特定白噪声后的经验模态分解称为NEEMD。分别以酵母和果蝇核小体定位分布谱作为输入信号,比较EMD、EEMD与NEEMD分解后IMF的方差与贡献率,以此作为模态混叠现象消除程度的评判标准。
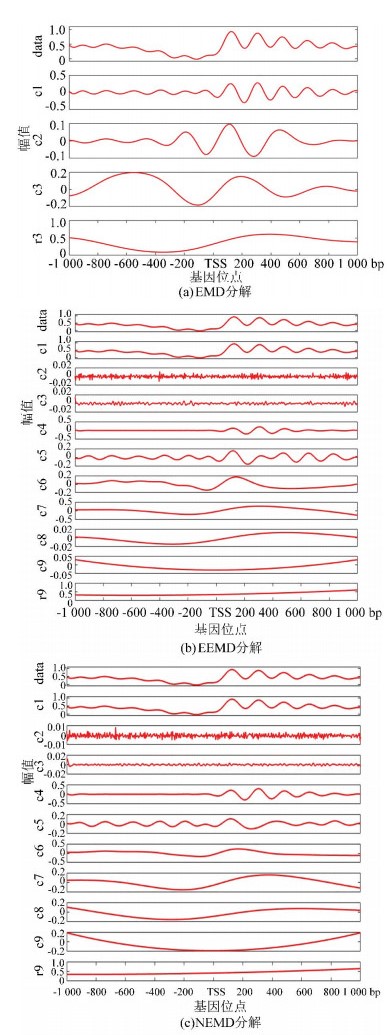
图 4(a)为EMD分解法的处理结果,通过EMD分解将信号分为4层,图中r4为分解4层之后余留下来的残余信号。从图中我们可以看到IMF1到IMF5都包含原始信号,我们无法区分哪一层具有原始信号信息最多。表 1与表 2显示IMF3的方差与贡献率是最大的,但是从图像上看IMF1具有原始信号信息最多,因此唯一的解释是使用EMD方法出现了模式混合现象。

|
图 4 核小体定位分布分解谱(酵母) Figure 4 Decomposition spectrum of nucleosome positioning distribution (Yeast) |
| 表 1 三种分解方法中IMF的方差(酵母) Table 1 IMFs' variance of three decomposition methods (Yeast) |
| 表 2 三种分解方法中IMF的贡献率(酵母) Table 2 IMFs' normalized variance of three decomposition methods (Yeast) |
图 4(b)为EEMD分解法的处理结果,添加的白噪声遵循很多参考文献中的建议值:添加白噪声次数为100,白噪声遵循高斯分布,幅值系数ε为0.2。由图像可以看出,IMF6和IMF7波形具有很强的相似性。
图 4(c)为NEEMD分解法处理的结果,根据核小体定位分布特点调整参数,选取添加高斯分布白噪声,噪声的次数为100,幅值系数ε为0.08。从实验结果看,该方法可以极大改善模态混叠现象。表 1与表 2证实了这一点:EEMD方法显示IMF1方差最大、贡献率最高,应该具有原始信号信息最多,NEEMD方法显示IMF1同样为方差最大、贡献率最高的一项,并且NEEMD中IMF1的贡献率比在EEMD更高。所以NEEMD相对于EEMD来说分解效果更好。
与酵母分解结果相对应,图 5(a)为果蝇核小体定位分布谱的EMD分解结果,图 5(b)为EEMD分解结果。在EEMD实验中,添加的白噪声参考了其它文献的建议值:添加白噪声次数为100,白噪声遵循高斯分布,幅值系数ε为0.2。图 5(c)为NEEMD分解结果。我们在实验中根据核小体定位分布特点调整了参数,选取添加噪声的次数为100,白噪声的幅值系数ε为0.08,噪声类型为瑞丽分布。尽管从分解图谱中不能直观看出改善程度,但是从表 3与表 4中可以得出以下结论:EMD方法显示IMF3贡献率最高,而图像直观显示IMF1与原始信号最为接近,所以具有模态混叠现象;EEMD方法显示IMF1方差最大、贡献率最高,在NEEMD方法中IMF1同样为方差最大、贡献率最高的一项,并且在NEEMD中IMF1贡献率比EEMD方法产生的IMF1更高,因此在应用于果蝇核小体定位分布时,NEEMD相较于EEMD就具有更好的分解效果。
|
图 5 核小体定位分布分解谱(果蝇) Figure 5 Decomposition spectrum of nucleosome positioning distribution (Drosophila) |
| 表 3 三种分解方法中IMF的方差(果蝇) Table 3 IMFs' variance of three decomposition methods (Drosophila) |
| 表 4 三种分解方法中IMF的贡献率(果蝇) Table 4 IMFs' normalized variance of three decomposition methods (Drosophila) |
以上实验表明:不同模型中加入白噪声的类型和幅度与所分解的数据相关,只有加入合适的白噪声,才能最大程度上改善模态混叠现象,提高分解的准确性。
2 核小体定位特征提取希尔伯特-黄变换(HHT)与傅里叶变换的相似之处在于,二者都是将时域中的信号进行解析后,便于从频域进行分析。在此,我们用希尔伯特-黄变换对核小体定位分布进行分析的目的是有二个:一是弥补傅里叶变换在频谱分析中的不足,二是通过HHT更深入研究两个物种核小体分布的频谱差异性。
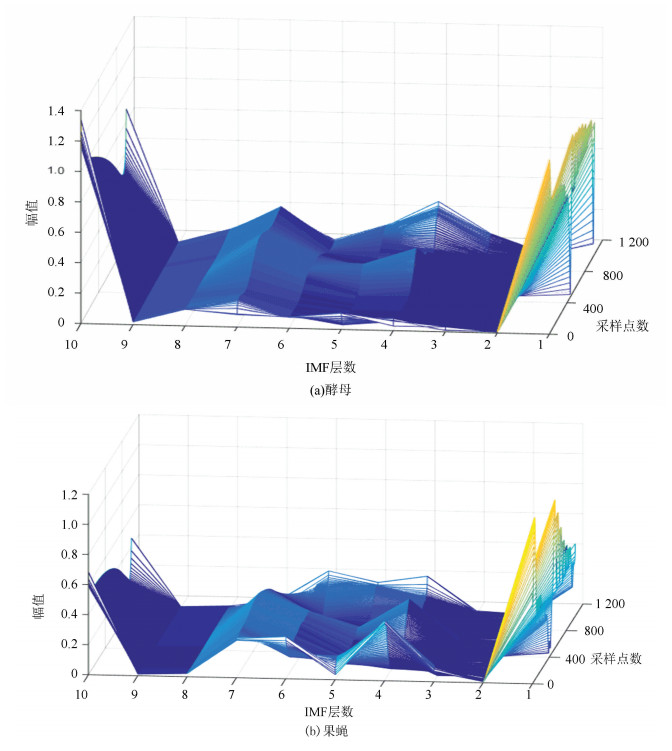
2.1 酵母与果蝇核小体定位信号的时域分解特征图 6(a)、(b)分别表示酵母与果蝇核小体定位信号的时域本征模态分解三维谱。从图中可以看出二个物种核小体定位信号在空间尺度上的细微差异,与果蝇相比较,在相同IMF分层下,酵母信号总体要平坦一些,信号曲面在复杂程度上要比果蝇低。以第4层分解结果为例,在同一层中,果蝇核小体定位信号的突起比酵母多,说明多细胞生物核小体组织的复杂程度要高于单细胞生物。
|
图 6 两种模式生物三维采样点-IMF层数-幅值谱 Figure 6 The 3D sample point-IMF layer number-amplitude spectrums of two model organisms |
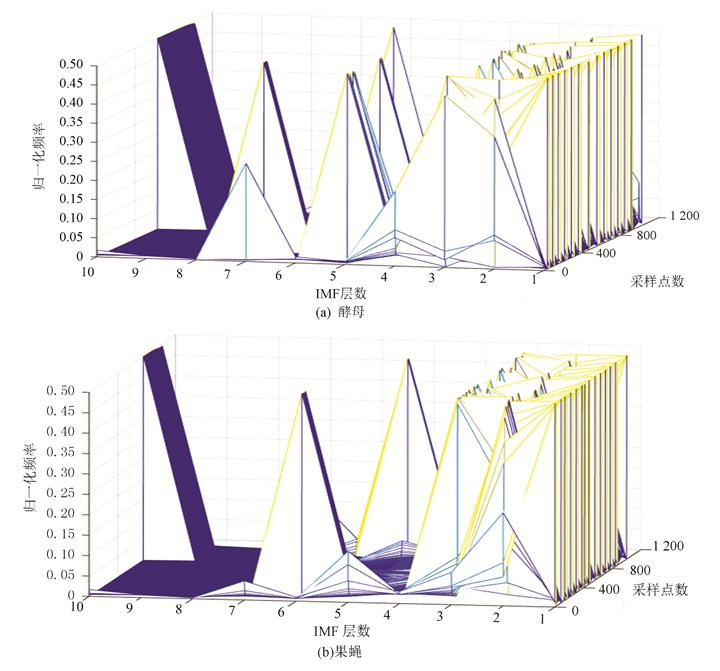
图 7(a)、(b)分别表示酵母与果蝇核小体定位信号的频域本征模态分解三维谱。从分层信号频谱分布可以看到,果蝇核小体定位信号成份中的高频部分要多于酵母。同样是在第五层信号中,酵母还保留了多个频率分量,而果蝇则少得多。这与时域分解特征得到的结论相一致,即果蝇的核小体排列相对酵母有更多的变化,也更为复杂。
|
图 7 两种模式生物三维采样点-IMF层数-频率谱 Figure 7 The 3D sample point-IMF layer number-frequency spectrums of two model organisms |
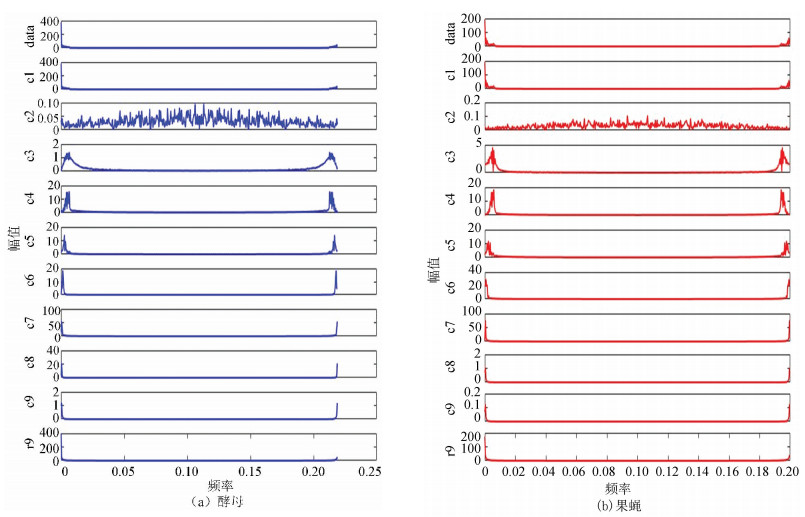
图 8(a)、(b)分别为酵母与果蝇核小体定位信号的二维幅频曲线。从图中每个IMF分量及剩余分量的幅频曲线可以看出两者在大体趋势上是相近的,在同等情况下都是分为9个IMF分量,且每个分量的幅频曲线趋势大致相同,这从某种程度上反应了生物在核小体组织上进化的保守性。
|
图 8 两种模式生物IMF幅频曲线 Figure 8 IMF amplitude frequency curve of two model organisms |
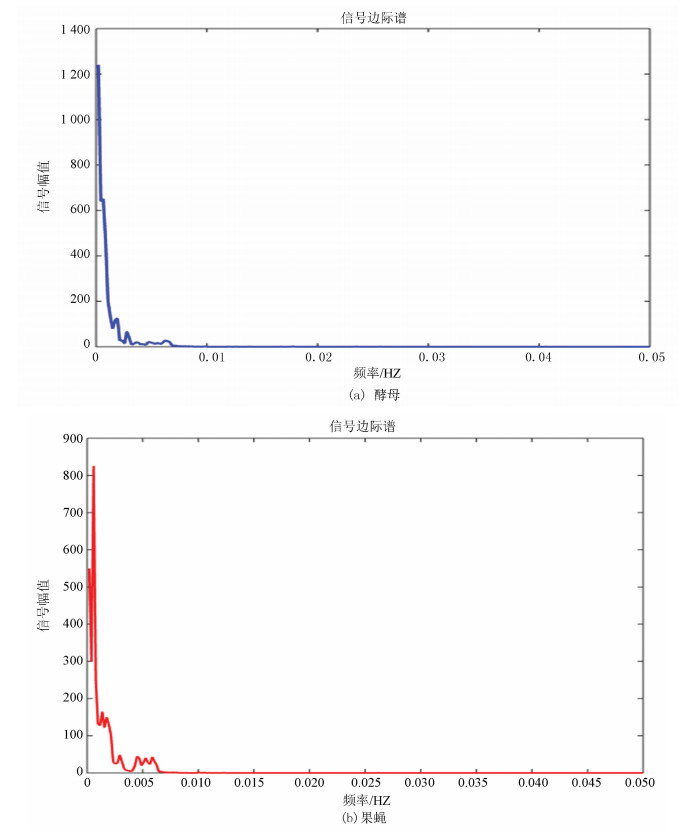
边际谱的定义是对Hilbert谱(二元函数)进行时间积分,积分结果是自变量w的一元函数,即幅值谱,它也描述信号的幅值在整个频率段上随频率的变化情况。边际谱的意义是信号中瞬时频率的总幅值的大小,将所有时刻某一频率的幅值加起来就是该频率的总幅值,即边际谱线的高度。
图 9(a)、(b)分别为酵母和果蝇核小体定位信号的边际谱,其走势进一步验证了两种模式生物进化过程具有的保守性,但是通过进一步研究发现虽然两者走势相同但是在0.002~0.003 Hz位置酵母只出现了一次最高峰,而果蝇在此处具有两个几乎相同的波峰,并且在0.005 Hz附近酵母的核小体定位模型只有一个小幅度的波峰,而果蝇的核小体定位模型出现了相对而言比较大幅度的上升,并且两个波峰也是几乎相同的。在信号幅值上酵母的骤减程度明显大于果蝇,相较于酵母而言,果蝇核小体定位模型信号幅值变化较为平缓。
|
图 9 两种模式生物边际谱 Figure 9 Marginal spectrum of two model organisms |
在某种程度上而言,边际谱的差异反映了生物从单细胞进化到多细胞过程中核小体组织形式发生的微妙变化。
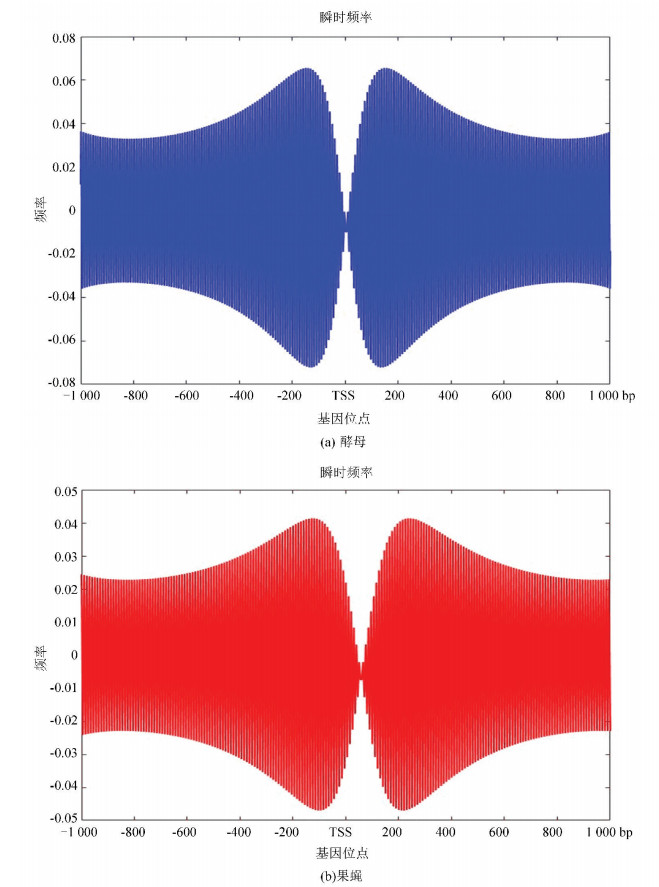
2.5 酵母与果蝇核小体定位信号的瞬时频率图 10(a)、(b)分别为酵母和果蝇核小体定位信号的瞬时频率。从图中看是大致相似的,在中心位置即转录起始位点TSS附近略有不同,酵母的核小体定位模型信号在转录起始位点急剧减小,而果蝇在TSS附近相对来说频率幅值缩降程度较小,或许体现了较为高等的生物在转录起始位点的自我保护机制,使得较为高等的真核模式生物在遭遇某种变故时能延缓自身的突变,以达到保护自身的作用。
|
图 10 两种模式生物瞬时频率 Figure 10 Instantaneous frequency of two model organisms |
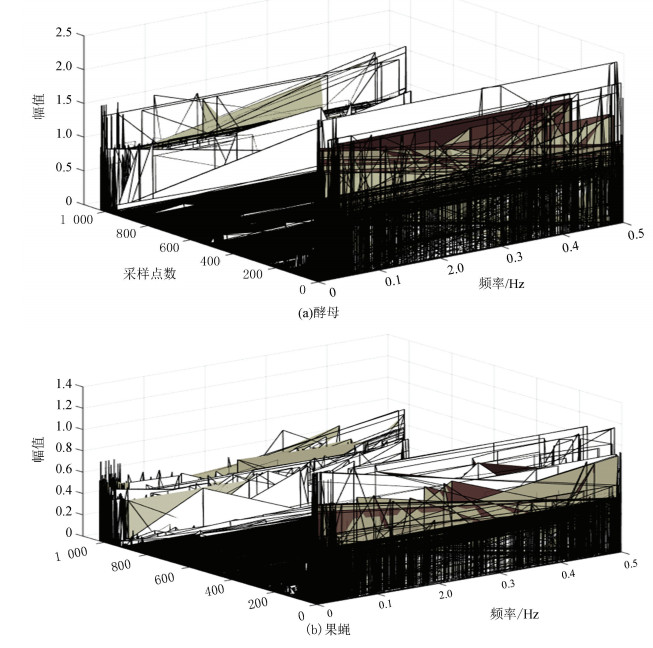
图 11(a)、(b)分别为酵母和果蝇核小体定位信号的HHT三维时频谱。其中X轴为归一化后的频率,Y轴为采样点数,Z轴为信号幅值。从图中可直观看出,果蝇的核小体定位分布比酵母更为复杂,但是它们的分布趋势是大致相似的,这从一定程度上再次印证了生物在核小体组织上进化的保守性。
|
图 11 两种模式生物HHT时频谱三维显示 Figure 11 The 3D HHT spectrums of two model organisms |
在生物进化过程中,由单细胞到多细胞核小体组织的演变既存在变异性也存在某种保守性,使得生物可以在保留优良特性的基础上加入某种抗干扰能力,适应生存需要。本文通过希尔伯特-黄变换(HHT)方法证实了生物进化结构与其复杂程度是一致的,通过HHT定量提取单细胞生物和多细胞生物核小体定位信号特征,进一步验证两物种之间在核小体组织结构上显著的差异性。
| [1] |
TESORO S, ALI I, MOROZOV A N, et al. A one-dimensional statistical mechanics model for nucleosome positioning on genomic DNA[J]. Physical Biology (S1478-3967), 2016, 13(1): 016004. DOI:10.1088/1478-3975/13/1/016004 (  0) 0) |
| [2] |
胡世赛, 陈宇翔, 张颖, 等. 酵母基因组核小体定位序列预测[J]. 生物物理学, 2018, 6(1): 1-6. HU Shisai, CHEN Yuxiang, ZHANG Ying, et al. Yeast genome nucleosome localization sequence prediction[J]. Biophysics, 2018, 6(1): 1-6. DOI:10.12677/BIPHY.2018.61001 (  0) 0) |
| [3] |
单秋甫, 丰继华, 卢英, 等. 果蝇胚胎期不同表达模式基因转录起始位点上游核小体的定位[J]. 生物物理学报, 2014, 30(1): 72-28. SHAN Qiufu, FENG Jihua, LU Ying, et al. Localization of nucleosomes upstream of transcription initiation sites of different expression patterns in Drosophila embryos[J]. Chinese Journal of Biophysics, 2014, 30(1): 72-28. DOI:10.3724/SP.J.1260.2014.30163 (  0) 0) |
| [4] |
KAPLAN N, MOORE I K, FONDUFE-MITTENDORF Y, et al. The DNA-encoded nucleosome organization of a eukaryotic genome[J]. Nature, 2008, 458(7236): 362-366. DOI:10.1038/nature07667 (  0) 0) |
| [5] |
BROGAARD K, XI L, WANG J P, et al. A map of nucleosome positions in yeast at base-pair resolution[J]. Nature, 2012, 486(7404): 120618151913005. DOI:10.1038/nature11142 (  0) 0) |
| [6] |
SCHWARTZ Y B, CAVALLI G. Three-dimensional genome organization and function in Drosophila[J]. Genetics(S0016-6731), 2017, 205(1): 5-24. DOI:10.1534/genetics.115.185132 (  0) 0) |
| [7] |
SCHEP A N, BUENROSTRO J D, DENNY S K, et al. Structured nucleosome fingerprints enable high-resolution mapping of chromatin architecture within regulatory regions[J]. Genome Research(S1088-9051), 2015, 25(11): 1757-70. DOI:10.1101/gr.192294.115 (  0) 0) |
| [8] |
NOBLE W, DUAN Z U, ANDRONESCU M, et al. A three-dimensional model of the yeast genome[J]. Nature(S0028-0836), 2016, 465(7296): 363. DOI:10.1007/978-3-642-20036-6_28 (  0) 0) |
| [9] |
丰继华, 郭亚茹, 牟锦, 等.真核模式生物核小体分布参数模型分析[J/OL].生物学杂志, 2019-06-13. http://kns.cnki.net/kcms/detail/34.1081.Q.20190613.1545.014.html. FENG Jihua, GUO Yaru, MOU Jin, et al. Analysis of the distribution parameter model of eukaryotic model bionuclei[J/OL]. Journal of Biology, 2019-06-13. http://kns.cnki.net/kcms/detail/34.1081.Q.20190613.1545.014.html. (  0) 0) |
| [10] |
VILLALOBOS S C, CAMARENA R G, LEM G. Crackle sounds analysis by empirical mode decomposition[J/OL]. IEEE Engineering in Medicine and Biology Magazine, 2007, (1-2): 40-47. DOI: 10.1109/MEMB.2007.289120.https://www.researchgate.net/publication/3246176.
(  0) 0) |
| [11] |
LI C, WANG X, TAO Z, et al. Extraction of time varying information from noisy signals: An approach based on the empirical mode decomposition[J]. Mechanical Systems & Signal Processing, 2011, 25(3): 812-820. DOI:10.1016/j.ymssp.2010.10.007 (  0) 0) |
| [12] |
LEE W, TILLO D, BRAY N, et al. A high-resolution atlas of nucleosome occupancy in yeast[J]. Nature Genetics(S1061-4036), 2007, 39(10): 1235-1244. DOI:10.1038/ng2117 (  0) 0) |
| [13] |
MAVRICH T N, JIANG C, IOSHIKHES I P, et al. Nucleosome organization in the Drosophila genome[J]. Nature(S0028-0836), 2008, 453(7193): 358-362. DOI:10.1038/nature06929 (  0) 0) |
| [14] |
张安安, 徐洋涛, 都健刚, 等. HHT分析局部放电信号时模态混叠的抑制[J]. 电力系统及其自动化学报, 2018, 30(5): 120-126. ZHANG Anan, XU Yangtao, DU Jiangang, et al. Modal aliasing suppression of HHT analysis of partial discharge signals[J]. Journal of Electric Power Systems and Automation, 2018, 30(5): 120-126. DOI:10.3969/j.issn.1003-8930.2018.05.019.-05 (  0) 0) |
| [15] |
CHEREJI R V, CLARK D D. Biophysical models of nucleosome positioning[J]. Biophysical Journal, 2015, 108(2): 537a. DOI:10.1016/j.bpj.2014.11.2946 (  0) 0) |
 2019, Vol. 17
2019, Vol. 17


