真核细胞内普遍存在着两种定位性质不同的核小体:即定位良好和定位模糊的核小体。二者的区别在于,定位良好的核小体包装DNA平均长度为147 bp左右,而定位模糊的核小体包装DNA长度不定。尽管随着生物实验技术的进步和成本的下降,不同物种的核小体定位数据在不断产生,但现阶段完全依靠实验方法检测核小体定位性质还面临着以下问题:(1)生物种类繁多,用实验方法检测所有生物的核小体位置是一项不可能完成的任务。(2)生物实验需要大量的人力、物力和时间投入,其成本和时效性是一大制约因素。(3)虽然现阶段实验数据的规模和丰富程度给核小体相关研究提供了极大支持,但仍不能满足部分研究人员希望即时获得自身关注领域数据的现实要求。因此,在基因组研究的某些领域使用计算机建模并进行预测,是对生物实验研究的有力补充,甚至是现阶段一项不可替代的工作。
对于核小体定位性质(定位良好与定位模糊)一般是根据生物实验数据进行研究的。Gan等人[1]于2014年首次从结构角度研究了核小体定位特征和模糊核小体性质,提出了一种基于连续小波变换(CWT)的核小体位置预测新方法(WaveNuc)。
研究表明,基因的转起始位点周围通常存在着一个保守的核小体缺失区域(NFR)[2-4],而在其上、下游区域的核小体则呈现出周期性排列[5-11]。我们根据现有核小体分布规律,对基因组转录起始位点周围的核小体分布建立了一个高精度复合正弦模型,并在前人所做的核小体位置预测工作基础上[12],以该分布模型作为遗传算法的寻优目标函数,以确定不同性质核小体分布中心及相邻区域,最终实现对局部核小体定位性质的预测。
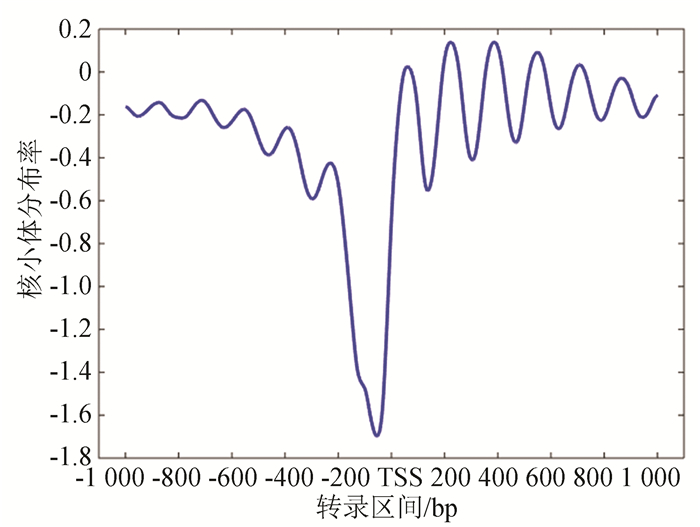
1 建立分布模型在使用遗传算法进行核小体定位性质预测之前,需要构建一个能真实反映核小体分布的数学模型。由于目前在核小体研究领域还未解决全基因组范围内定位良好和定位模糊核小体的分布问题。面对这一难题,我们首先注意到一个普遍事实,即无论是单细胞的酵母,还是多细胞的果蝇,甚至是属于高等哺乳动物的人类,其核小体在基因启动子周围的组织形式都是高度保守和近似的[13](见图 1)。
|
图 1 酵母转录起始位点的核小体分布图谱 Figure 1 Nucleosome distribution map of yeast transcription initiation site |
酵母转录起始位点的核小体分布图谱来源于Lee等人于2007年做出的酵母核小体高分辨率占位率实验数据[20]。基因的转录起始位点据来源于David等人提出的4 792个高置信度转录数据[21]。
1.2 拟合函数的选取为了提取核小体组织形式,我们分别对多项式、傅里叶级数、高斯函数和正弦函数的拟合效果进行了比较。以上四种拟合方式实验结果如图 2所示,其中(a)、(b)、(c)、(d)分别代表多项式拟合、傅里叶拟合、高斯拟合和正弦函数拟合。

|
图 2 四种拟合函数对比图 Figure 2 Comparison of four fitting functions |
在图 2的拟合结果中,多项式拟合精度最低(图 2(a))。傅里叶拟合图像与核小体分布图像具有一定的相似性(图 2(b)),但是位于转录起始点下游的区域拟合未能捕获原分布特征,即在远离转录起始位点两端的区域拟合程度较差。图 2(c)是高斯函数拟合的结果,在转录区域高斯函数拟合的相似性较高,但在转录起始位点上游区域拟合误差最大。
图 2(d)使用的是正弦函数进行的拟合,拟合图像几乎与实测核小体分布图谱完全重合,仅在上游区域远离TSS的区域存在拟合误差。
表 1列出了五种拟合函数的性能指标。分别是:和方差(SSE)、拟合优度(Rsquare)、标准差(Rmse)、自由度(Dfe)及校正决定系数(Adjrsquare)。其中,和方差和标准差越接近于0,说明拟合出的数据与原始分布数据越相似。
| 表 1 四种拟合函数性能指标(酵母) Table 1 Performance indicators of four fitting functions (Yeast) |
而拟合优度与校正决定系数越接近于1时,拟合的效果越好。通过比较,可知使用正弦函数拟合的核小体分布图效果最好。
本文采用的复合正弦函数为:
| $ f(x)=\sum\limits_{n=1}^{9} A_{n} \sin \left(\omega_{n} x+\varphi_{n}\right) $ | (1) |
对上述拟合模型拟合后得到的最优参数见表 2。
| 表 2 正弦拟合函数参数列表(酵母) Table 2 List of sine fitting function parameters (Yeast) |
在前人所做的核小体位置预测的基础上[12],我们利用遗传算法寻找分布模型中的极值点,其代表两种不同性质核小体的分布中心。
具体方法:(1)首先随机产生200个个体作为初始种群,为了简化计算,使用的是常规二进制编码。(2)在遗传算子的选择上,交叉算子选用均匀交叉,变异算算子采用离散变异算法。我们测试后发现交叉概率选取区间为[0.7, 0.9],变异率选取[0.001, 0.1],遗传算法无论在收敛速度上,还是精度上都达到了实验预期。结果见表 3和表 4。
| 表 3 遗传算法搜索到的波峰位置 Table 3 Veak position searched by genetic algorithm |
| 表 4 遗传算法搜索到的波谷位置 Table 4 Valley location found by genetic algorithm |
获得表 3和表 4所示的分布中心后,我们将按以下假设判别个体基因上的核小体定位性质:
(1) 转录起始位点周围核小体分布谱的波峰中心及其邻近区域,是定位良好核小体的最可能出现的范围。如果支持向量机预测到核小体可能出现的区域与其重合,且连续范围达到120-160 bp左右,可判别为定位良好的核小体。
(2) 相反,如果核小体分布谱的波谷中心及其邻近区域与核小体预测区域重合,且连续范围大于160 bp,则可判断为定位模糊的核小体。
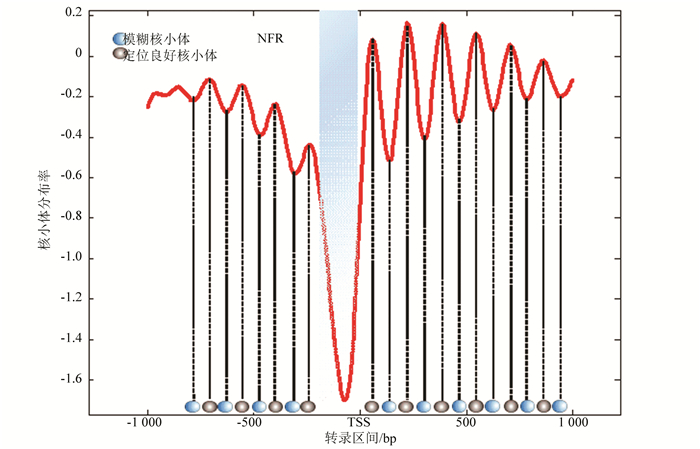
图 3是示意了在转录起始位点(TSS)上下游各取1 000 bp的区域,通过拟合函数辨识出定位良好核小体和模糊核小体的分布中心,其中黑色椭圆代表定位良好的核小体最可能出现的位置,蓝色为定位模糊的核小体最可能出现的位置。从总体辨识结果观察,定位良好核小体和模糊核小体在转录起始点周围区域遵循着“间隔平均,交替出现”的规律。
|
图 3 转录起始位点周围核小体预测示意图 Figure 3 Schematic diagram of nucleosome prediction around the transcription start site |
图 3中,分布模型曲线中的蓝色阴影区域表示核小体缺失区域(NFR),波峰对应定位良好的核小体,波谷对应定位模糊的核小体。
将单个基因上预测到可能存在核小体的区域与模板进行比对,当波峰区域与存在核小体区域重叠时,可以认为这一区域有较高概率出现定位良好的核小体;反之,当波谷区域与存在核小体区域重叠,那么表明这一区域有较高概率出现定位模糊的核小体;如果模板中无论是波峰还是波谷区域均不存在核小体时,那么可以认为这些区域是连接DNA。
根据上述方法,我们绘制了核小体定位性质预测示意图(见图 4),图中最上端是预测模板,(a)、(b)、(c)、(d)分别代表是第三条染色体上,随机选取的4个基因(YCL027W、YCL040W、YCR054W和YCR066W)的转录区域,蓝色区域是由支持向量机根据DNA物理性质预测到的核小体可能出现的区域。图 4中,通过拟合函数波峰与波谷周围构成的预测模板,将基因划分为不同的区域,如果预测到的核小体出现在波峰区域,且满足判定条件,可判别为定位良好,而出现在波谷区域则判别为定位模糊。通过以上方法,可以对全基因组转录起始位点周围的核小体预测结果进行定位性质判别。为了证明以上方法的正确性,我们将不同性质核小体区域与生物实验数据做了比较,在此阳性样本定义为预测区间内确实出现与该区间同性质的核小体,反之则为阴性样本,并使用了以下统计指标[23]:真阳性(TP),假阳性(FP),真阴性(TN),假阴性(FN),

|
图 4 核小体预测性质定位示意图 Figure 4 Schematic diagram of nucleosome prediction properties |
| $ 真样本灵敏度:{\rm{S}}{{\rm{n}}^ + } = {\rm{TP}}/({\rm{TP}} + {\rm{FN}}) $ | (2) |
| $ 负样本灵敏度:{\rm{S}}{{\rm{n}}^ - } = {\rm{TN}}/({\rm{TN}} + {\rm{FP}}) $ | (3) |
| $ 真样本特异度:{\rm{S}}{{\rm{p}}^ + } = {\rm{TP}}/({\rm{TP}} + {\rm{FP}}) $ | (4) |
| $ 负样本特异度:{\rm{S}}{{\rm{p}}^ - } = {\rm{TN}}/({\rm{TN}} + {\rm{FN}}) $ | (5) |
| $ 准确率:{\rm{Ac = }}\frac{{{\rm{ TP + TN}}}}{{{\rm{TP + TN + FP + FN}}}} $ | (6) |
马修斯相关系数:
| $ \begin{array}{l} {\rm{MCC}} = \\ \frac{{{\rm{ TPXIN - FPXFN }}}}{{\sqrt {({\rm{TP}} + {\rm{FN}}) \times ({\rm{TP}} + {\rm{FN}}) \times ({\rm{TN}} + {\rm{FN}}) \times ({\rm{TN}} + {\rm{FN}})} }} \end{array} $ | (7) |
预测的四种基因的性能指标如表 5所示。
| 表 5 评价指标 Table 5 Evaluation indicators |
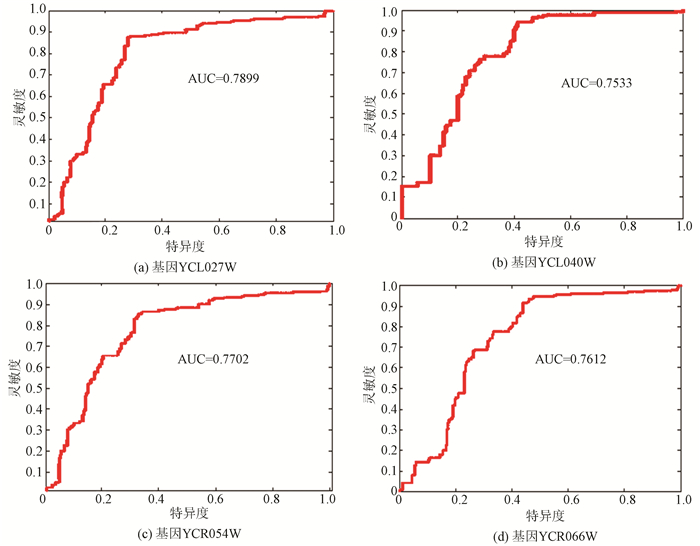
实验结果显示阳性样本所占比例即准确率(Ac)均以超过80%,说明此预测方法有效。图 5为ROC曲线。
由图 5看出四种基因的ROC曲线的得分均大于0.75,进一步说明预测结果具有统计意义,实现了核小体的性质判别,达到了预期的准确率和实验目的。
|
图 5 四种基因的预测结果ROC曲线图 Figure 5 ROC graph of prediction results of four genes |
根据转录起始位点核小体分布先验知识,建立拟合函数后,利用遗传算法搜索极值,确定出核小体定位性质划分模板,可有效辨别出定位良好和模糊的核小体位置。通过结果分析,证明了我们的方法在局部区域是行之有效的,是对模糊核小体预测工作进行的一次有益尝试。
| [1] |
GAN Y, ZOU G, GUAN J, et al. A novel wavelet-based approach for predicting nucleosome positions using DNA structural information[J]. IEEE/ACM Transactions on Computational Biology & Bioinformatics, 2014, 11(4): 638-647. DOI:10.1109/tcbb.2014.2306837 (  0) 0) |
| [2] |
BERNSTEIN B E, LIU C L, HUMPHREY E L, et al. Global nucleosome occupancy in yeast[J]. Genome Biology, 2004, 5(9): R62. DOI:10.1186/gb-2004-5-9-r62 (  0) 0) |
| [3] |
YUAN G C, LIU F J, DION M F, et al. Genome-scale identification of nucleosome positions in S. cerevisiae[J]. Science, 2005, 309(5734): 626-630. DOI:10.1126/science.1112178 (  0) 0) |
| [4] |
SORIANO I, QUINTALES L, ANTEQUERA F. Clustered regulatory elements at nucleosome-depleted regions punctuate a constant nucleosomal landscape in Schizosaccharomyces pombe[J]. BMC Genomics, 2013, 14(1): 813. DOI:10.1186/1471-2164-14-813 (  0) 0) |
| [5] |
LEE C K, SHIBATA Y, RAO B, et al. Evidence for nucleosome depletion at active regulatory regions genome-wide[J]. Nature Genetic, 2004, 36(8): 900-905. DOI:10.1038/ng1400 (  0) 0) |
| [6] |
IOSHIKHES I P, ALBERT I, ZANTON S J, et al. Nucleosome positions predicted through comparative genomics[J]. Nature Genetic, 2006, 38(10): 1210-1215. DOI:10.1038/ng1878 (  0) 0) |
| [7] |
JIN H, RUBE H T, SONG J S. Categorical spectral analysis of periodicity in nucleosomal DNA[J]. Nucleic Acids Research, 2016, 44(5): 2047-2057. DOI:10.1093/nar/gkw101 (  0) 0) |
| [8] |
FEDOSEYEVA V B, ALEXANDROV A A. Large-scale periodicity of nucleosome positioning signal in pericentric regions of chromosomes (Drosophila melanogaster)[J]. Journal of Biomolecular Structure & Dynamics, 2014, 32(12): 2042-2050. DOI:10.1080/07391102.2013.844081 (  0) 0) |
| [9] |
CHEREJI R V, MOROZOV A V. Ubiquitous nucleosome crowding in the yeast genome[J]. Proceedings of the National Academy of Sciences of the United States of America, 2014, 111(14): 5236. DOI:10.1073/pnas.1321001111 (  0) 0) |
| [10] |
SALIH B, TRIPATHI V, TRIFONOV E N. Visible periodicity of strong nucleosome DNA sequences[J]. Journal of Biomolecular Structure and Dynamics, 2015, 33(1): 1-9. DOI:10.1080/07391102.2013.855143 (  0) 0) |
| [11] |
TRIPATHI V, SALIH B, TRIFONOV E N. Universal full-length nucleosome mapping sequence probe[J]. Journal of Biomolecular Structure & Dynamics, 2015, 33(3): 666-673. DOI:10.1080/07391102.2014.891262 (  0) 0) |
| [12] |
肖建平, 丰继华, 卢英, 等. 基于核小体位置预测的酵母进化印迹研究[J]. 生物信息学, 2013, 11(02): 150-152, 160. XIAO Jianping, FENG Jihua, LU Ying, et al. Study on yeast evolutionary imprinting based on nucleosome position prediction[J]. Chinese Journal of Bioinformatics, 2013, 11(02): 150-152, 160. DOI:10.3969/j.issn.1672-5565.2013.14 (  0) 0) |
| [13] |
BOEGER H, GRIESENBECK J, STRATTAN J S, et al. Nucleosomes unfold completely at a transcriptionally active promoter[J]. Molecular Cell, 2003, 11(6): 1587-1598. DOI:10.1016/s1097-2765(03)00231-4 (  0) 0) |
| [14] |
WEINER A, HUGHES A, YASSOUR M, et al. High-resolution nucleosome mapping reveals transcription-dependent promoter packaging[J]. Genome Research, 2010, 20(20): 90-100. DOI:10.1101/gr.098509.109 (  0) 0) |
| [15] |
HELBO A S, LAY F D, JONES P A, et al. Nucleosome positioning and NDR structure at RNA polymerase Ⅲ promoters[J]. Scientific Reports, 2017(7): 41947. DOI:10.1038/srep41947 (  0) 0) |
| [16] |
DREOS R, AMBROSINI G, BUCHER P. Influence of rotational nucleosome positioning on transcription start site selection in animal promoters[J]. Plos Computational Biology, 2016, 12(10): e1005144. DOI:10.1371/journal.pcbi.1005144 (  0) 0) |
| [17] |
ICHIKAWA Y, MOROHASHI N, TOMITA N, et al. Sequence-directed nucleosome-depletion is sufficient to activate transcription from a yeast core promoter in vivo[J]. Biochemical & Biophysical Research Communications, 2016, 476(2): 57-62. DOI:10.1016/j.bbrc.2016.05.063 (  0) 0) |
| [18] |
WANG B, HU Y. Promoter-targeted small activating RNAs alter nucleosome positioning[J]. Advances in Experimental Medicine & Biology, 2017, 983: 53. DOI:10.1007/978-981-10-4310-9_4 (  0) 0) |
| [19] |
CHEREJI R V, CLARK D J. Major determinants of nucleosome positioning[J]. Biophysical Journal, 2018, 114(10): S0006349518303813. DOI:10.1016/j.bpj.2018.03.015 (  0) 0) |
| [20] |
LEE W, TILLO D, BRAY N. A high-resolution atlas of nucleosome occupancy in yeast[J]. Nature Genetics, 2007, 39(10): 1235-1244. DOI:10.1038/ng2117 (  0) 0) |
| [21] |
DAVID L, HUBER W, GRANOVSKAIA M. A high-resolution map of transcription in the yeast[J]. Proceedings of the National Academy of Sciences of the United States of America, 2006, 103(14): 5320-5325. DOI:10.1073/pnas.0601091103 (  0) 0) |
| [22] |
THASTROM A, BINGHAM L M, WIDOM J. Nucleosomal locations of dominant DNA sequence motifs for histone-DNA interactions and nucleosome positioning[J]. Journal of Molecular Biology, 2004, 338(4): 695-709. DOI:10.1016/j.jmb.2004.03.032 (  0) 0) |
| [23] |
GAO S, ZHANG N, DUAN G Y, et al. Prediction of function changes associated with single-point protein mutations using support vector machines (SVMs)[J]. Human Genome Variation Society, 2009, 30(8): 1161-1166. DOI:10.1002/humu.21039 (  0) 0) |
 2019, Vol. 17
2019, Vol. 17


