随着计算机设备的发展和在人类日常生活中的广泛应用,人工智能的进一步发展和人机交互的无缝化和自由化都聚焦到人体动作识别这一领域。人体动作识别的目的是为了判断人类的意图同时做出相应服务,需要通过计算机对人体的各类动作、姿态或者运动模式进行自动检测、分析和解读。
在神经系统的支配下,多组肌群相互协调、共同配合完成人体的每一个动作,在相应的肌群会产生肌电信号(Electromyography,EMG)。表面肌电信号作为一种无创测量的肌电信息检测办法,随着各种相关技术水平的发展,以及国内外对肌电信号的不断深入研究,其广泛应用于临床医学、康复医学和假肢的控制等领域,取得了许多研究成果。近年来,应用于表面信号领域的模式识别算法主要包括模糊模式识别(Fuzzy pattern recognition,FPR)[1]算法、线性判别分析(Linear discriminant analysis,LDA)[2]算法、人工神经网络(Artificial neural networks,ANN)[3]算法和支持向量机(Support vector machine,SVM)[4-5]算法等,研究成果颇丰。
1 FPR算法FPR是从模糊数学诞生后在模式识别领域的活跃应用。基于模糊性的本质在于事物类属的不确定性和对象资格程度的渐变性,模糊模式识别在处理一些信息分类问题上,能自适应提取模糊规则,不受初始化参数的影响。目前,主要研究方法是针对一些模糊识别问题设计相应的模糊识别系统,以及用模糊数学对传统模式识别中的一些方法进行改进。
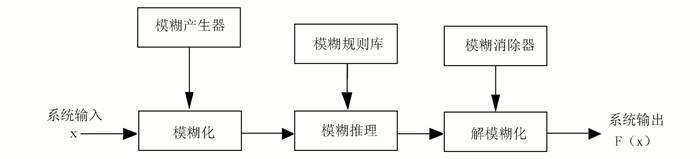
1.1 模糊分类器系统模型如图 1所示,模糊逻辑系统(Fuzzy inference system, FIS)通过模糊产生器对系统输入进行模糊化,再经模糊逻辑系统后输出,模糊逻辑系统完成模糊推理和解模糊化两步操作。
|
图 1 模糊推理系统模型 Figure 1 Fuzzy inference system model |
依据“高木-关野”模糊系统模型,构建一个模糊推理分类器,其规则如下:
| $ \begin{array}{*{20}{c}} {Rl:{x_1} = {u^l}_1\left( {{x_1}} \right)}\\ {{x_2} = {u^l}_2\left( {{x_2}} \right)}\\ {{x_d} = {u^l}_d\left( {{x_d}} \right)}\\ {{y^l} = {a^l}_0 + {a^l}_1{x_1} + \cdots + {a^l}_d{x_d}\left( {l = 1, 2, \cdots , M} \right)} \end{array} $ | (1) |
系统输出为:
| $ f\left( x \right) = \frac{{\sum\limits_{l = 1}^M {{y^l}[\prod\limits_{i = 1}^d {{u^l}_i({x_i})} ]} }}{{\sum\limits_{l = 1}^M {[\prod\limits_{i = 1}^d {{u^l}_i({x_i})} ]} }} $ | (2) |
定义均方误差准则函数MSE为:
| $ MSE = \frac{1}{2}\sum\limits_{n = 1}^N {{{[f\left( {{x_n}} \right) - \hat f]}^2}} $ | (3) |
根据最小均方误差准则,求解MSE,即训练分类器模型,由梯度下降算法[7],得到分类器的各个参数的迭代修正公式[8-9]。由梯度下降算法得到:
| $ \alpha \left( {k + 1} \right) = \alpha \left( k \right) - {\alpha _4}{X^{\rm{T}}}\left( {X\alpha - y} \right) $ | (4) |
| $ \begin{array}{l} \alpha = \left[ {\begin{array}{*{20}{c}} {{\alpha ^1}_0}&{{\alpha ^2}_0}& \cdots &{{\alpha ^{\rm{M}}}_0}\\ {{\alpha ^1}_1}&{{\alpha ^1}_1}& \cdots &{{\alpha ^{\rm{M}}}_1}\\ \vdots&\vdots&\ddots&\vdots \\ {{\alpha ^1}_d}&{{\alpha ^1}_d}& \cdots &{{\alpha ^{\rm{M}}}_d} \end{array}} \right]\\ X = \left[ {\begin{array}{*{20}{c}} 1&{{X_{11}}}& \cdots &{{X_{1d}}}\\ 1&{{X_{21}}}& \cdots &{{X_{2d}}}\\ \vdots&\vdots&\ddots&\vdots \\ 1&{{X_{n1}}}& \cdots &{{X_{nd}}} \end{array}} \right]\\ y = \left[ {\begin{array}{*{20}{c}} {{y^1}_1}&{{y^2}_1}& \cdots &{{y^{\rm{M}}}_1}\\ {{y^1}_2}&{{y^2}_2}& \cdots &{{y^{\rm{M}}}_2}\\ \vdots&\vdots&\ddots&\vdots \\ {{y^1}_n}&{{y^2}_n}& \cdots &{{y^{\rm{M}}}_n} \end{array}} \right] \end{array} $ |
其中,n为训练样本个数;α4为常系数。
1.3 模糊规则的提取办法常用模糊规则提取方法有基于K-means聚类的方法[10]和基于神经网络的方法[11]两种。基于K-means聚类的模糊规则提取方法中的K就代表聚类中心个数,连同计算得到的对应簇的各维方差,模糊分类器的参数得以初始化。这种方法有两大缺点:一是需要人为设定聚类数K;二是聚类结果易受设置的初始点的影响。因而,当无法获取训练样本的特征空间分布时,K-means聚类算法的使用存在很大的局限性。
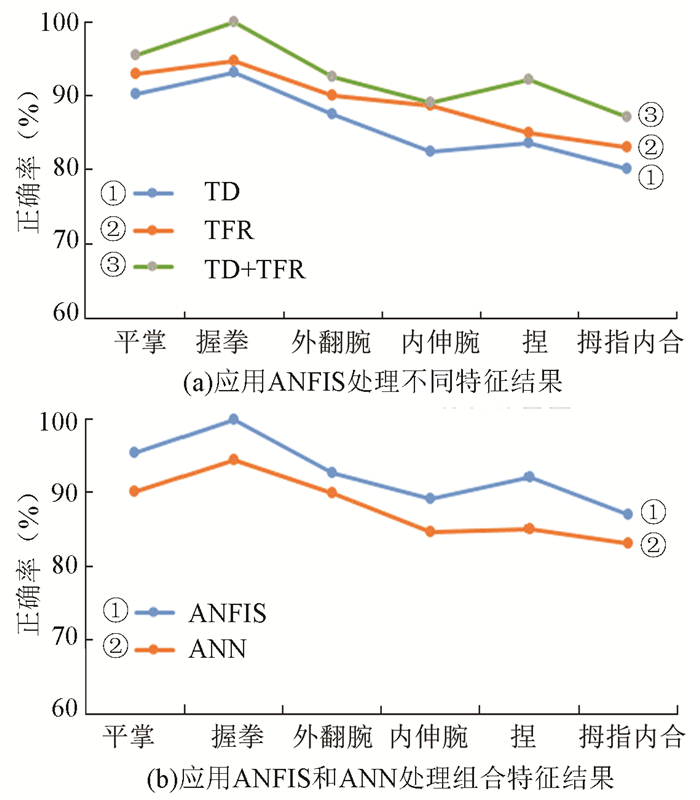
Khezri M, Jahed M[13]采取第二种方法,结合人工神经网络,应用基于表面肌电信号的神经-模糊推理(ANFIS)系统, 很好地解决了上述两大问题。图 2(a)验证了神经模糊分类器处理时域和时频域特征的组合时识别效果最佳,图 2(b)表示同时采用ANFIS和基于ANN的分类器对比6种手势动作的时域和时频域组合特征进行了分类处理,ANFIS分类器分类正确率均明显高于ANN分类器。但与此同时,应用ANFIS来从神经元网络中提取模糊规则,分类处理时间开销较大。
|
图 2 不同特征和分类器类型对手部动作识别结果对比 Figure 2 Comparison diagram for the recognition results of selected hand movements from classifiers of different features and types |
LDA的主要概念是通过将m维描述符空间分离为由线性判别函数定义的超平面分隔的两个区域来对依赖性进行分类。LDA最小化属于同一类别的矢量之间的距离,并使等级中心之间的距离最大化。应用LDA算法设计的线性判别分类器(LDC)是基于最小风险贝叶斯准则的马氏距离分类器[14],是线性分类器的典型代表[15]。在类别概率分布确定的情况下,该分类器可以达到最小的分类错误率[16]。该分类器不需要任何参数调整,并提供计算效率的实时操作[6, 12]。
Alomari F, Liu G.[29]使用来自sEMG信号的不同提取特征对8个手部动作进行分类,实验结果显示,样品熵,均方根,肌细胞百分率和差异绝对标准偏差值的组合特征,使用线性判别分析方法分类率达到98.56%。
尽管实验已经取得很高的分类率,在该分类器的训练过程中,依旧存在一些问题,若已知样本的概率分布前提下,训练大量样本也会带来巨大的时间开销,这个不足也阻碍其进一步的应用。
3 ANN算法人工神经网络仿照生物神经元结构和神经信息的传递机理,是由多个简单,高度互联的神经元组成的计算系统,是以经验风险最小化原则进行的。应该注意的是,神经元数量不足可能导致网络无法对复杂数据进行建模,导致模型拟合不佳。同时,过多的神经元可能导致训练时间变得非常长,导致模型对提供的数据过度拟合。目前在模式识别中应用人工神经网络时,神经元数量的选取显得尤为重要,结合一定的方法和实验可以选取较为合适的神经元数量。现在较为常用的ANN算法有BP神经网络[3, 17-18]、Elman神经网络[19-20]、非线性自回归神经网络(NSRX)[21]等。
3.1 BP神经网络人工神经网络的发展受到生物神经网络的启发,可以解决预测、控制、优化、聚类和模式识别等各种问题。在这几种类型的培训方法中,反向传播(Backpropagation, BP)被用于这项工作。作为一种常用的神经网络算法,BP神经网络就是运用BP算法进行训练和学习的人工神经网络[22]。基本原理就是通过使用误差函数的导数最小化网络的误差来发挥作用。反向传播是一种受监督的培训形式,并通过网络计算衍生物流向量。BP神经网络采用的三层网络结构[17]见图 3。

|
图 3 神经网络拓扑结构 Figure 3 Neural network topology |
应用过程中,BP算法在一定程度上受到局部最小化影响,Yang L, Tian Y等运用模拟退火算法[23]优化BP神经网络分类器,对7种手势动作提取时域特征(EMG积分,方差和三阶AR模型系数)和频域特征(功率谱),作为改进BP神经网络分类器的输入,有效提高BP算法在多模式识别中的分类正确率。
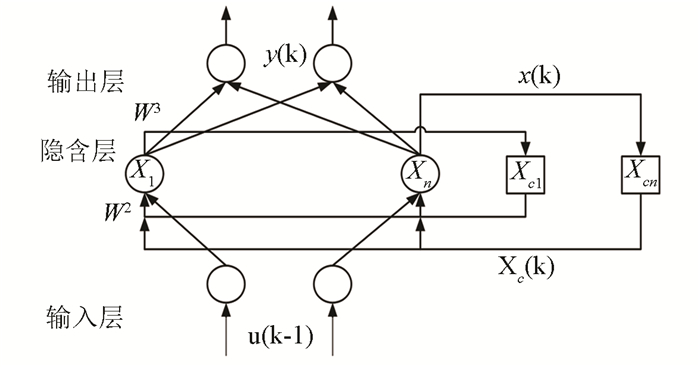
3.2 Elman神经网络Elman网络可以看作是一种具有局部记忆单元和局部反馈连接的前向神经网络[24]。如图 4所示,该网络相比传统的神经网络,除了具有输入层、隐含层和输出层外,还多出了一个联系单元,该层暂且称为关联层,如图 3所示。
|
图 4 Elman神经网络结构示意图 Figure 4 Elman neural network structure diagram |
关联层接收来自隐含层对应连接点的反馈信号,同时存储记忆所在时刻的隐含层的状态。下一时刻,隐含层的输入将是关联层记忆下的隐含层状态和当前时刻的输入,这样完成反馈置入。类似时延算子,Elman网络通过时延和存储,能够处理动态信息,赋予该网络动态机理功能。应用于无模型控制的基于粒子群优化的Elman神经网络能有效的减小跟踪误差,同时控制信号有较好的收敛性与控制精度[25]。
4 SVM算法 4.1 SVM算法原理Vapnik提出一种新的方法称为支持向量机(SVM),他的理论在1995~1998年被进一步完善[26]。SVM的原理是通过使用非线性映射,将原始空间的数据转换成较高维度的特征空间,其中样本是线性可分离的,提出SVM实现结构风险最小化(SRM),具有解决非线性、高维小样本等问题的特殊优势。此外,由于SVM的决策依赖于样本中的SVM,SVM可以很好地应用于不平衡样本数据的分类。SVM算法采用内核函数映射方法,其属性通过内核函数的种类进行测量。给定一个数据集G={xi, di}ni=1,xi是输入向量,di是例外值,n是数据点的数量。当用于模式识别问题时,SVM运用以下等式并求取最大值:
| $ Q\left( a \right) = \sum\limits_{i = 1}^n {{a_i} - \frac{1}{2}} \sum\limits_{i,j = 1}^n {{a_i}{a_j}{y_i}{y_j}} K\left( {{x_i},{x_j}} \right) $ | (5) |
约束条件:
| $ \sum\limits_{i = 1}^n {{a_i}{y_i} = 0,} {a_i} \ge 0,i = 1,2, \cdots ,n $ | (6) |
获取最佳分类:
| $ f\left( x \right) = {\mathop{\rm sgn}} \left\{ {\sum\limits_{i = 1}^n {{a_i}{y_i}K\left( {{x_i},x} \right) + b} } \right\} $ | (7) |
其中,sgn(·)是符号函数,符号在f(x)中的变化表示不同类型。K(xi, x)是内部函数(IPKF),不同的IPKF组成不同的算法。内核函数的选择隐含地确定映射特征空间的属性,内核函数的参数和形式导致学习机器类型和复杂性,因此内核函数是影响SVM性能的最重要因素之一。常用的内核函数包含多项式内核(PK),Sigmoid内核(SK)和高斯内核(GK)等。
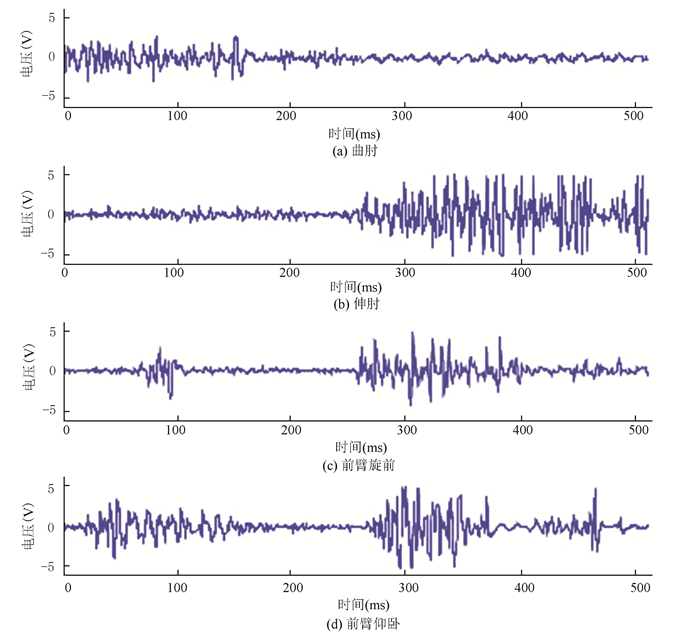
4.2 SVM算法应用SVM算法最初是为二分类问题设计的,当处理多类问题时,需要构造合适的多类分类器,主要是通过组合多个二分类器来实现多分类器的构造,常见方法有“一对多”法和“一对一”法。一对多法处理一对多的训练集,存在加高的分类误差。一对一法在对位置样本进行分类时,处理效果较好,但会因为样本类别较多而需要训练较多的SVM,开销较大。近年来,SVM的研究方向主要集中在完善其本身性质以及加深深度和拓宽广度。截至目前,SVM在气体识别等问题都有成功的应用,是肌电假肢多运动模式识别成功应用的重要根据[27]。如图 5分别为曲肘、伸肘、前臂旋前和前臂仰卧四个动作的表面肌电信号数据。
|
图 5 四种不同手臂动作的表面肌电信号样本数据 Figure 5 Sample sEMG data of four different arm movements |
A. Alkan, M. Günay[28]提取四种上肢动作的时域特征平均绝对值,再分别运用5种不同的判别分析分类器和SVM进行了分类识别,正确率和错误率对比结果如表2。表中显示,前文中提到的判别分析分类器的不同类型方法对单一时域特征的分类正确率均不超过98%,而应用SVM分类器效果更好,对这四种动作的分类正确率高达99%,表示SVM在对基于肌电信号的动作识别方面有着独特的优势。
| 表 1 分类结果:基于不同类型的判别分析分类器和SVM的训练(误差)和10倍错误率 Table 1 Classification results:Training (resubstitution) and 10-fold error rates for different types of classifiers based on the discriminant analysis and SVM |
1) 本文中,应用各类算法都有着较好的分类能力,但为了提高分类识别正确率,基于表面肌电信号的人体动作识别需要进行多模式处理,单一的时域特征或者频域特征已经无法满足这一需求,寻找更多的表面肌电信号的典型特征,结合时频域特征,增加特征数量,是提高多模式识别正确率的关键。
2) 在大量算法中,ANN算法可以解决复杂的分类问题,学习能力强大,在肌电控制、知识工程等很多领域得到了很好的应用,而与小波分析,混沌,分形理论等的融合更是现阶段的研究热点,有着广阔的应用前景。
3) 与传统统计学为基础的ANN相比,SVM不涉及概率测度和大数定律等,支持向量的数目决定了其计算的复杂性。应用这两种算法都能较好的进行分类,但SVM处理小样本、非线性的高维数据优势明显,计算速度快。
| [1] |
KHEZRI M, JAHED M. A novel approach to recognize hand movements via sEMG patterns [C]. International Conference of the IEEE Engineering in Medicine & Biology Society. US: IEEE, 2007, 4907. DOI: 10.1109/IEMBS.2007.4353440.
(  0) 0) |
| [2] |
张启忠, 席旭刚, 马玉良, 等. 基于表面肌电信号的手腕动作模式识别[J]. 中国生物医学工程学报, 2013, 32(3): 257-265. ZHANG Qizhong, XI Xugang, MA Yuliang, et al. Study on wrist's multi-movement pattern recognition based on sEMG[J]. Chinese Journal of Biomedical Engineering, 2013, 32(3): 257-265. DOI:10.3969/j.issn.0258-8021.2013.03.01 (  0) 0) |
| [3] |
MANE S M, KAMBLI R A, PROF F S K, et al. Hand motion recognition from single channel surface EMG using wavelet & artificial neural network ☆[J]. Procedia Computer Science, 2015, 49(1): 58-65. DOI:10.1016/j.procs.2015.04.227 (  0) 0) |
| [4] |
LUCAS M F, GAUFRIAU A, PASCUAL S, et al. Multi-channel surface EMG classification using support vector machines and signal-based wavelet optimization[J]. Biomedical Signal Processing & Control, 2008, 3(2): 169-174. DOI:10.1016/j.bspc.2007.09.002 (  0) 0) |
| [5] |
洪洁, 王璐, 汪超, 等. 基于人工鱼群算法优化SVM的手部动作sEMG识别[J]. 传感器与微系统, 2016, 35(2): 23-25. HONG Jie, WANG Lu, WANG Chao, et al. Recognition of sEMG hand actions based on artificial fish swarm algorithm optimized SVM[J]. Transducer and Microsystem Technologies, 2016, 35(2): 23-25. DOI:10.13873/J.1000-9787(2016)02-0023-03 (  0) 0) |
| [6] |
PHINYOMARK A, QUAINE F, CHARBONNIER S, et al. EMG feature evaluation for improving myoelectric pattern recognition robustness[J]. Expert Systems with Applications, 2013, 40(12): 4832-4840. DOI:10.1016/j.eswa.2013.02.023 (  0) 0) |
| [7] |
李太福, 熊隽迪. 基于梯度下降法的自适应模糊控制系统研究[J]. 系统仿真学报, 2007, 19(6): 1265-1268. LI Taifu, XIONG Jundi. Sudy on adaptive fuzzy control system based on gradient descent learning algorithm[J]. Journal of System Simulation, 2007, 19(6): 1265-1268. DOI:10.3969/j.issn.1004-731X.2007.06.022 (  0) 0) |
| [8] |
丁世飞, 史忠植, 靳奉祥. 非线性迭代PLS信息模式识别算法[J]. 计算机工程, 2008, 34(1): 20-22. DING Shifei, SHI Zhongzhi, JIN Fengxiang. Information Pattern Recognition Algorithm Based on Nonlinear Iterative PLS[J]. Computer Engineering, 2008, 34(1): 20-22. DOI:10.3969/j.issn.1000-3428.2008.01.007 (  0) 0) |
| [9] |
CHAN F H, YANG Y S, LAM F K, et al. Fuzzy EMG classification for prosthesis control[J]. IEEE Transactions on Rehabilitation Engineering A Publication of the IEEE Engineering in Medicine & Biology Society, 2000, 8(3): 305-311. DOI:10.1109/86.867872 (  0) 0) |
| [10] |
WONG C C, CHEN C C, YEH S L. K-means-based fuzzy classifier design[C]. IEEE International Conference on Fuzzy Systems, 2000. US: IEEE, 2000: 48-52. DOI: 10.1109/FUZZY.2000.838632.
(  0) 0) |
| [11] |
LI W, HORI Y. An algorithm for extracting fuzzy rules based on RBF neural network[J]. Control Engineering of China, 2006, 53(4): 1269-1276. DOI:10.1109/TIE.2006.878305 (  0) 0) |
| [12] |
KAUFMANN P, ENGLEHART K, PLATZNER M. Fluctuating emg signals: investigating long-term effects of pattern matching algorithms[C]. International Conference of the IEEE Engineering in Medicine and Biology. US: IEEE, 2010: 6357-6360. DOI: 10.1109/IEMBS.2010.5627288.
(  0) 0) |
| [13] |
KHEZRI M, JAHED M. A neuro-fuzzy inference system for sEMG-Based identification of hand motion commands[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1952-1960. DOI:10.1109/TIE.2010.2053334 (  0) 0) |
| [14] |
张谢锴, 丁世飞. 基于马氏距离的孪生多分类支持向量机[J]. 计算机科学, 2016, 43(03): 49-53. ZHANG Xiekai, DING Shifei. Mahalanobis distance-based twin multi-calss classification support vector machine[J]. Computer Science, 2016, 43(03): 49-53. DOI:10.11896/j.issn.1002-137X.2016.3.009 (  0) 0) |
| [15] |
LIU C, WECHSLER H. Evolutionary pursuit and its application to face recognition[J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 2000, 22(6): 570-582. DOI:10.1109/34.862196 (  0) 0) |
| [16] |
张振平, 宣国荣, 郑俊翔, 等. 一种基于最小分类错误率的改进型LDA特征选择算法[J]. 微型电脑应用, 2005, 21(4): 4-6. ZHANG Zhenping, XUAN Guorong, ZHENG Junxiang, et al. An improved LDA feature selection algorithm based on minimum classification error rate[J]. Microcomputer Applications, 2005, 21(4): 4-6. DOI:10.3969/j.issn.1007-757X.2005.04.002 (  0) 0) |
| [17] |
于擎, 杨基海, 陈香, 等. 基于BP神经网络的手势动作表面肌电信号的模式识别[J]. 生物医学工程研究, 2009, 28(1): 6-10. YU Qing, YANG Jihai, CHEN Xiang, et al. Pattern recognition of gesture's surface myoelectrogram signal based on BP neural networks[J]. Journal of Biomedical Engineering Research, 2009, 28(1): 6-10. DOI:10.3969/j.issn.1672-6278.2009.01.002 (  0) 0) |
| [18] |
罗志增, 加玉涛. 基于表面EMG功率谱和BP网络的多运动模式识别[J]. 华中科技大学学报(自然科学版), 2006, 34(7): 63-66. LUO Zhizeng, JIA Yutao. Multi-pattern recognition by using surface electormyography's power spectra and BP neural networks[J]. Journal Huanzhong University of Science & Technology(Nature Science Edition), 2006, 34(7): 63-66. DOI:10.3321/j.issn:1671-4512.2006.07.020 (  0) 0) |
| [19] |
SHI X H, LIANG Y C, LEE H P, et al. Improved elman networks and applications for controlling ultrasonic motors[J]. Applied Artificial Intelligence, 2004, 18(7): 603-629. DOI:10.1080/08839510490483279 (  0) 0) |
| [20] |
于亚萍, 孙立宁, 张峰峰, 等. 基于小波变换的多特征融合sEMG模式识别[J]. 传感技术学报, 2016, 29(4): 512-518. YU Yaping, SUN Lining, ZHANG Fengfeng, et al. sEmg pattern recognition based on multi feature fusio of wavelet transform[J]. Chinece Journal of Senxors and Actuators, 2016, 29(4): 512-518. DOI:10.3969/j.issn.1004-1699.2016.04.009 (  0) 0) |
| [21] |
王红旗, 李林伟, 毛啊敏. 基于小波包的表面肌电信号特征表示与识别[J]. 计算机工程与应用, 2015, 51(09): 217-220. WANG Hongqi, LI Linwei, MAO Amin. Feature representation and recognition of SEMGS based on wavelet packet[J]. Computer Engineering and Applications, 2015, 51(09): 217-220. DOI:10.3778/j.issn.1002-8331.1406-0223 (  0) 0) |
| [22] |
杨新亮, 罗志增. 基于表面肌电信号的时频组合特征融合识别[J]. 华中科技大学学报(自然科学版), 2011, 39(s2): 153-156. YANG Xinliang, LUO Zhizeng. A recognition method of multi-channel SEMG based on the fusion of time-frequency combination characteristics[J]. Journal Huanzhong University of Science & Technology (Nature Science Edition), 2011, 39(s2): 153-156. DOI:10.13245/j.hust.2011.s2.044 (  0) 0) |
| [23] |
TAJBAKHSH A, ESHGHI K, SHAMSI A. A hybrid PSO-SA algorithm for the traveling tournament problem[J]. European J of Industrial Engineering, 2012, 6(6): 512-518. DOI:10.1109/ICCIE.2009.5223865 (  0) 0) |
| [24] |
时小虎, 梁艳春, 徐旭. 改进的Elman模型与递归反传控制神经网络[J]. 软件学报, 2003, 14(6): 1110-1119. SHI Xiaohu, LIANG Yanchun, XU Xu. An improved elman model and recurrent back-propagation control neural networks[J]. Journal of Software, 2003, 14(6): 1110-1119. DOI:10.13328/j.cnki.jos.2003.06.012 (  0) 0) |
| [25] |
张俊玲, 陈增强, 张青. 基于粒子群优化的Elman神经网络无模型控制[J]. 智能系统学报, 2016, 11(01): 49-54. ZHANG Junling, CHEN Zengqiang, ZHANG Qing. Elman model-free control method based on particle swarm optimization algorithm[J]. CAAI Transactions on Intelligent Systems, 2016, 11(01): 49-54. DOI:10.11992/tis.201507025 (  0) 0) |
| [26] |
QIAN H, MAO Y, XIANG W, et al. Recognition of human activities using SVM multi-class classifier[J]. Pattern Recognition Letters, 2010, 31(2): 100-111. DOI:10.1016/j.patrec.2009.09.019 (  0) 0) |
| [27] |
汪丹, 张亚非. SVM和BP算法在气体识别中的对比研究[J]. 传感技术学报, 2005, 18(1): 201-204. WAN Dan, ZHANG Yafei. Research of gas classification based on SVM compared with BP[J]. Chinese Journal of Sensors and Actuators, 2005, 18(1): 201-204. DOI:10.3969/j.issn.1004-1699.2005.01.052 (  0) 0) |
| [28] |
ALKAN A, GVNAY M. Identification of EMG signals using discriminant analysis and SVM classifier[J]. Expert Systems with Applications, 2012, 39(1): 44-47. DOI:10.1016/j.eswa.2011.06.043 (  0) 0) |
| [29] |
ALOMARI F, LIU G. Analysis of extracted forearm sEMG signal using LDA, QDA, K-NN classification algorithms[J]. Open Automation & Control Systems Journal, 2014, 6(1): 108-116. DOI:10.2174/1874444301406010108 (  0) 0) |
 2018, Vol. 16
2018, Vol. 16


