随着蛋白质数据量的不断扩大,如何从蛋白质序列中提取出有用的生物信息是目前比较紧急重要的任务。蛋白质二级结构[1]是蛋白质形成稳定构象的重要基础,是研究蛋白质序列的重要前提。进而为研究蛋白质的功能以及相互作用模式提供基础,蛋白质研究的进一步发展有利于新药的研发,所以蛋白质的二级结构预测是目前的重要工作。
在蛋白质二级结构预测方面,已有许多的研究方法。基于残基构象性的Chou-Fasman算法[2]和以信息论作为基础的GOR算法[3],都是单序列预测方法。Qian[4]于1988年用人工神经网络进行预测,得到的准确率在60%以上。吴玉明[5]提取氨基酸的理化特征和倾向因子,采用支持向量机(SVM)进行预测,得到的预测准确率为70.7%。利用kb-prossp-nn算法,对数据CB396的预测准确率为82%[6]。文献[7]中,作者组合特定位置打分矩阵信息和深度学习网络架构,得到的预测准确率为80.7%。
文献[8]中,作者运用动态贝叶斯分类器来进行蛋白质二级结构预测。并且引入了动态贝叶斯分类器稀疏参数算法,得到的预测准确率为76.3%。文献[9]中,作者将支持向量(SVM)和贝叶斯分类器结合起来进行蛋白质二级结构预测,实验数据为RS126数据集。文献[10]中,作者对SARS数据集进行实验,用支持向量机(SVM)进行蛋白质二级结构预测,得到的OvO准确率为89.27%。作者用支持向量机(SVM)对位置特异性打分矩阵(Position specific scoring matrix, PSSM)进行蛋白质二级结构预测,实验数据为CB513,得到的预测准确率为76.11%[11]。
本实验中,将基团编码与PSSM数据组合一起得到的新的编码方式,分别进行自动编码器和贝叶斯分类器进行预测。
1 新的编码方式 1.1 基团编码本文按照含有氨基酸内部组成结构信息的基团表,对氨基酸进行编码(见表 1),基团编码由42个属性组成。
| 表 1 氨基酸名称简写表 Table 1 Short names of amino acids |
表 2中的1表示带环基团的编号,共37个。表中2表示各个基团中含有的原子名称。表中3表示含有对应基团的氨基酸名称简写。表格1中第3列中的I1类表示是L、P、F、W、Y、E、R、K、H、M、N、D、Q等13个氨基酸。“起始”是指蛋白质序列中的第一个氨基酸,“终止”是指蛋白质序列中的终止氨基酸。
| 表 2 不带环基团信息表 Table 2 Information of the radical group without band |
表 3中的1表示剩余不带环基团的编号,2表示含有这个基团的氨基酸名称,3表示基团中含有的原子名称。
| 表 3 带环基团信息表 Table 3 Information of the radical group with band |
本文对氨基酸的编码方式:氨基酸A,根据已知的基团信息表,氨基酸A含有的基团包括2, 4, 6, 7几个位置,那么42位编码中需要在2, 4, 6, 7几个位置用1表示,剩余的位置则用0表示,42位基团编码010101100000000000000000000000000000000000可以表示氨基酸A。编码氨基酸C,根据基团信息表可以发现,出现氨基酸C的基团编号是2, 4, 6, 10等4个位置,在42位编码中2, 4, 6, 10几个位置上用1来表示,其余位置用0来表示,那么可以用编码010101000100000000000000000000000000000000表示氨基酸C。
依照这种方法依次对20种氨基酸进行编码,可以总结得到基团编码(见表 4)。
| 表 4 氨基酸-基团编码对应表 Table 4 the radical group encoding method |
就其中一条蛋白质来说,如果序列中含有m个氨基酸,在对基团编码进行滑动窗口设置时,在数据前后补0。将滑动窗口数选为15时,需要在氨基酸序列前后分别补上7个0,, 依次对序列从前到后进行滑动窗口选取数据,生成42*15维的数据,则这条蛋白质可以表示为m*630。
1.3 PSSMPSI-BLAST是BLAST的变种[12],并且通过蛋白质的功能特征搜索蛋白质序列数据库中的相关序列,并且这些相关序列的相似性太远是BLAST搜索不到的。
位置特异性打分矩阵(Position specific scoring matrix, PSSM)是通过PSI-Blast搜索nr数据库后,计算联配中每个位点的新得分建立的,含有丰富的生物进化信息。在本文试验中,选用Blosum 62进化矩阵来进行实验。在实验时,选取Blosum62矩阵的前20列,这样假设其中一条蛋白质长度为m,则PSSM矩阵表示为m*20。对PSSM数据取滑动窗口为13时,需要在蛋白质序列前后分别补上6个0,依次对序列从前到后进行滑动窗口选取数据,生成20*13维的数据,则这条蛋白质可以表示为m*260。将基团编码与位置特异性得分矩阵组合在一起,得到新的编码方式。如果某一条蛋白质长度为m,如果取滑动窗口数为13时,42位基团编码数据是m*546,位置特异性打分矩阵(PSSM)数据为m*260。将两组数据组合在一起组成新的蛋白质序列编码为m*806。
1.4 DSSP结构DSSP结构划分方法在蛋白质二级结构预测中使用的较为广泛,DSSP[13]由Wolfgang Kabsch于1983年提出的, DSSP含有8种结构状态,分别是B(β桥)、C(非B, E, G, H, I, S或T)、E(β折叠)、G(310螺旋)、H(α螺旋)、I(π螺旋)、S(转角)、T(β转角)。在实际试验中会将这8种结构状态进行简化,比较常用的简化划分方法有5种,(1)H是H,E是E,其它都是C;(2)H是H, B、E是E,其它都是C;(3)G、H是H,E是E,其它都是C;(4)G、H是H,B、E是E,其它都是C;(5)G、H、I是H,B、E是E,其它都是C。
在本文试验中,将选取G、H、I是H,B、E是E,其它都是C的结构状态划分方法。
1.5 预测指标实验中选取的蛋白质准确率预测的定义指标是Q3和Qi(i分别是C、E、H这3个类别)[14]:
| $ {Q_3} = \frac{{{\rm{T}}{{\rm{P}}_{\rm{C}}} + {\rm{T}}{{\rm{P}}_{\rm{E}}} + {\rm{T}}{{\rm{P}}_{\rm{H}}}}}{T} $ | (1) |
| $ {Q_i} = \frac{{{\rm{T}}{{\rm{P}}_i}}}{{{\rm{T}}{{\rm{P}}_i} + {\rm{F}}{{\rm{P}}_i}}} $ | (2) |
其中,i为C、E、H中的某一类,可以得到每个类别的准确率。TPi表示某个状态被准确预测出的残基数,T表示蛋白质序列中含有的残基总数。
2 自动编码器深度学习是具有人工神经网络特点的学习方法,作为在深度学习中广泛运用的自动编码器,自动编码器具有层次结构的特点,是一种多层前传神经网络。自动编码器由Rumelhart于1986年提出,用于处理高维复杂的数据,可以对高维的实验数据进行降维处理,得到低维特征向量[15-16],然后将得到的特征向量送入分类器中。
自动编码器[17]包括输入层、隐含层、输出层。输入层和输出层含有相同的维度,都是m维,隐含层则为n维。隐含层神经元数要比输入层神经元数多,则需要隐含层神经元具有稀疏性。需要加入稀疏性限制,确保隐含层的大部分是被抑制的状态。
针对原始数据X,经过学习、调整参数、映射之后得到新的数据Y。在编码过程中,得到隐含层的表达:
| $ Z = {s_e}\left( {{W^1}X + {b^1}} \right) $ | (3) |
其中,se是编码过程中的激活函数,通常选用sigmoid函数。W1为权值向量,b1为偏差量。
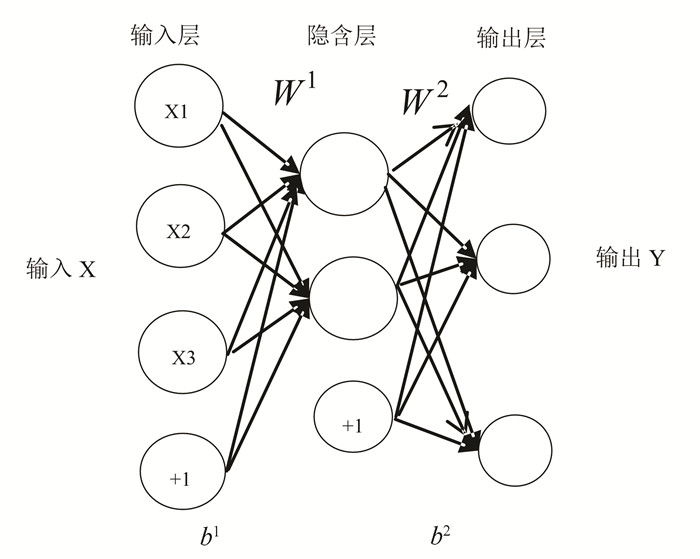
|
图 1 单层自动编码器结构图 Figure 1 The structure of single-layer auto encoder |
再对映射后的表达Z进行反向加权映射,即对隐含层得到的表示进行重构。在解码过程中,可以得到与原始输入具有相同维度的新的表达:
| $ Y = {s_d}\left( {{W^2}Y + {b^2}} \right) $ | (4) |
其中,sd为解码过程中的激活函数,选用sigmoid函数。通常W1与W2互为转置,可以表示为W1T=W2。
W2为权重向量,b2为偏差量,自动编码器在训练过程中寻找参数θ={W, b1,b2}。
重构得到的新的表达Y相当于在已知Z表达的条件下,对输入数据X的预测,这样的重构存在误差。自动编码器中的学习过程就是使重构后得到的输出尽量还原输入层的数据,即使表达Z与表达X尽量相同。重构错误有其方法可以量化,重构中的误差函数选择均方误差函数:
| $ E = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_i}-{y_i}} \right)}^2}} $ | (5) |
其中,N是样本总数。
期望值(稀疏度值)可以用ρ表示[18],每个神经元i的平均激活度可以表示为:
| $ {{\hat \rho }_i} = \frac{1}{N}\sum\limits_{j = 1}^N {y_i^1\left( {{x_j}} \right)} = \frac{1}{N}\sum\limits_{j = 1}^N {{s_e}\left( {{w_i}^{{1^T}}{x_j} + b_i^1} \right)} $ | (6) |
其中,N是训练样本总数,Xj是第j个训练样本,bi1是b1偏差量中的第i个偏差量。当
| $ KL\left( {\rho \left\| {{{\hat \rho }_i}} \right.} \right) = \rho \log \left( {\frac{\rho }{{{{\hat \rho }_i}}}} \right) + \left( {1-\rho } \right)\log \left( {\frac{{1-\rho }}{{1-{{\hat \rho }_i}}}} \right) $ | (7) |
KL函数是衡量这两个数值之间距离大小关系的函数,它随着
| $ \sigma = \frac{1}{2}\sum\limits_l^L {\sum\limits_{j = 1}^N {\sum\limits_c^p {\left( {w_{jc}^{{l^2}}} \right.} } } $ | (8) |
其中,L表示隐含层数,在本文实验中隐含层设置为1层。N是样本总数,p表示训练中的变量数,即输入样本的维度m。稀疏编码器中的损失函数可以表示为:
| $ J = E + \lambda * \sigma + \beta \sum\limits_{j = 1}^m {KL\left( {{{\hat \rho }_j}\left\| \rho \right.} \right)} $ | (9) |
其中β为控制稀疏性正则化的系数,在本文实验中的取值为4。λ为控制权重正则化系数,本文实验中取值为0.06。ρ是稀疏度值,试验时取值为0.06。在经过自动编码器得到特征向量后,将特征向量送入到贝叶斯分类器中得到预测准确率。在实验中,选择了单层编码器来获得特征向量。由于在实验中,将自动编码器的隐含层数设置为了1 500,所以送入贝叶斯分类器的输入数据为1 500维。
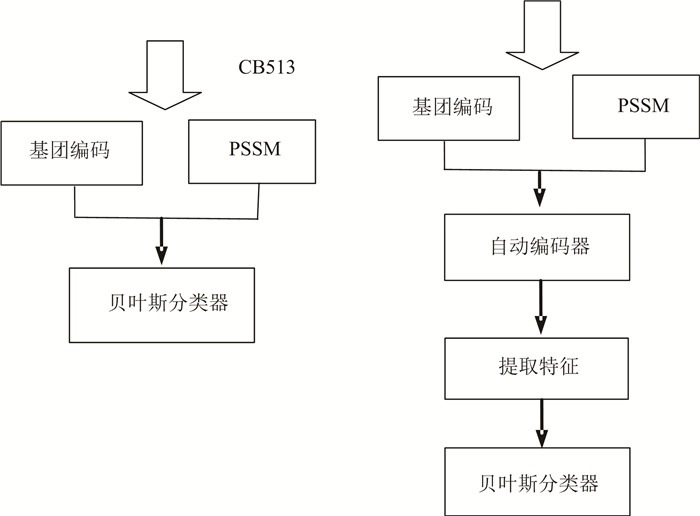
|
图 2 数据的处理方法图 Figure 2 The data processing process |
实验中,对数据进行两种方法进行预测,一种是将基团编码与PSSM矩阵组合后直接送入贝叶斯分类器中进行预测,输入的维度就是实际数据的维度。如果选取13个滑动窗口,其中一条蛋白质长度为m,则输入贝叶斯分类器中的维度为m*806。一种是将基团编码与PSSM矩阵组合后的数据送入自动编码器中,提取特征,如果隐含层设置的神经元数为1 500,则提取到的特征数为m*1 500,然后将提取到的特征送入贝叶斯分类器中进行预测。
3 贝叶斯分类器贝叶斯分类器是用来分类的贝叶斯网络,它的原理[19]通过先验概率、条件概率和贝叶斯公式得到后验概率。贝叶斯分类器处理一个C分类问题,在本文实验中,蛋白质的二级结构是一个3分类问题,即C值C = 1, 2, 3。如果每个类别的先验概率是已知的,它是P(Xi)(i= 1, 2, 3),条件概率密度P(Y|Xi)(i = 1, 2, 3),用贝叶斯公式,可以计算出的后验概率:
| $ P\left( {{X_i}\left| Y \right.} \right) = \frac{{P\left( {Y\left| {{X_i}} \right.} \right)P\left( {{X_i}} \right)}}{{\sum {P\left( {Y\left| {{X_j}} \right.} \right)P\left( {{X_j}} \right)} }} $ | (10) |
试验中选用的数据集为CB513[20]数据集和25PDB[21]数据集。CB513数据集中共含有513条蛋白质,其中蛋白质序列的相似度小于25%。25PDB数据集是典型的非冗余数据集,其序列相似度小于25%。25PDB数据集共包括1 673条蛋白质序列,其中43条蛋白质序列为空,最后的实验过程中采用1 640条蛋白质序列。在实验过程中需要将蛋白质数据进行3折交叉验证,即将所有数据分为3份,选取其中任意2份为训练集,则剩余1份作为测试集。然后将实验数据分别用自动编码器和贝叶斯分类器进行实验,得到两组数据。
4.1 结果分析 4.1.1 CB513数据结果1) 在对CB513数据进行实验,将513条蛋白质共包括84 119个氨基酸,随机进行3折交叉验证,其中训练样本含有342条蛋白质,测试样本含有171条蛋白质。当滑动窗口数为13时,由基团编码42*13,PSSM编码20*13,组合生成新的编码方式,即546+260=806,则输入向量的维度为806维,送入贝叶斯分类器中得到实验结果(见表 5)。
| 表 5 CB513贝叶斯分类器结果 Table 5 The accuracy of Bayes classifier |
2) 用单层自动编码器试验时,对基团编码与PSSM组合形成的新的编码数据进行3折交叉验证。当滑动窗口为13时,单个隐含层神经元设置为1 500,控制稀疏性正则化系数为4,权重正则化系数为0.06,稀疏度值为0.06。得到的特征向量数据为1 500维,然后送入贝叶斯分类器中(见表 6)。
| 表 6 CB513自动编码器结果 Table 6 The accuracy of single-layer auto encoder |
1) 对25PDB数据进行实验时,数据共包括1 640条蛋白质序列。进行3折交叉验证,当滑动窗口数为15时,由基团编码维度42*15,PSSM编码维度20*15,组合生成新的编码方式,维度为630+300=930维,则输入向量的维度为930维,送入贝叶斯分类器中得到实验结果(见表 7)。
| 表 7 25PDB贝叶斯分类器结果 Table 7 The accuracy of Bayes classifier |
2) 用单层自动编码器试验时,对基团编码与PSSM组合形成的新的编码数据进行3折交叉验证。单个隐含层神经元设置为1 500,控制稀疏性正则化系数为4,权重正则化系数为0.06,稀疏度值为0.06。得到的特征向量数据为1 500维,然后送入贝叶斯分类器中(见表 8)。
| 表 8 25PDB自动编码器结果 Table 8 The accuracy of single-layer auto encoder |
根据结果分析CB513数据(见图 3),发现当滑动窗口数不同时,贝叶斯分类器结果在70.56%~70.98%。使用自动编码器时,准确率在71.18%~71.95%。比较两组分类器结果,当滑动窗口数为13时,自动编码器的准确率比贝叶斯分类器要高出1.39%。分析数据25pdb时,贝叶斯分类器的结果在71.54%~71.92%,自动编码器准确率在73.04%~73.19%。当滑动窗口数为13时,自动编码器的预测准确率比贝叶斯分类器要高1.66%。随着蛋白质序列数量的增加,25pdb的贝叶斯分类器结果要比CB513数据的结果高出0.98%。25pdb数据的自动编码器结果要比CB513的结果高出1.7%(见图 4)。由于在实验中,用到的分类器都是贝叶斯分类器,可以发现,经过自动编码器得到特征向量后用贝叶斯分类器进行分类的结果要比单独经过贝叶斯分类器的结果要高1.66%。而且随着蛋白质序列的增加,二级结构预测准确率也会得到提升。
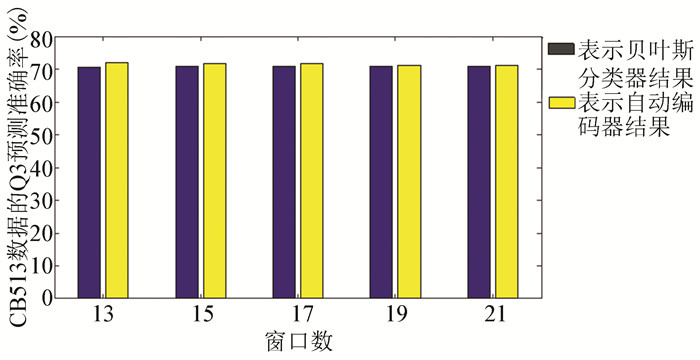
|
图 3 CB513数据的实验直方图 Figure 3 Histogram of CB513 |
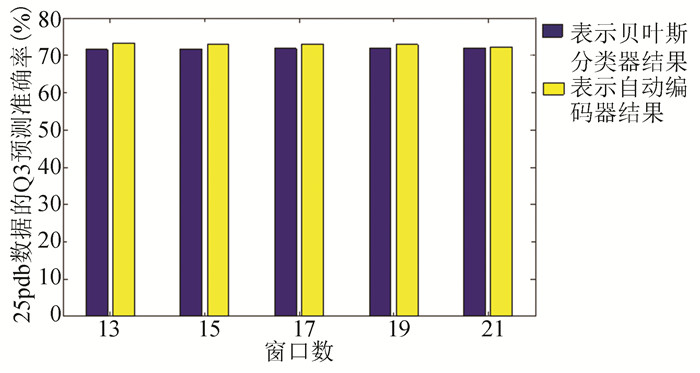
|
图 4 25pdb数据的实验直方图 Figure 4 Histogram of 25pdb |
与文献[11]相比,作者使用支持向量机预测特异性位置打分矩阵(PSSM)得到的预测率更高一些。本文首先在DSSP结构划分上不一样,选取的划分方法是是所有五种划分结构中准确率最低的,导致预测结果有所下降。其次我们用自动编码器提取特征之后用贝叶斯分类器进行预测,贝叶斯分类器的处理速度比支持向量机更快。
5 结论通过两组数据的直方图可以发现:
1) 本文提出组合基团编码与PSSM数据的新的编码方式,然后选取不同的分类器进行实验。
2) 选择单层自动编码器和贝叶斯分类器对这种新的编码方式进行预测分类,其中自动编码器的稀疏度参数选取的比较小,自动编码器的预测准确率比贝叶斯分类器结果要高出1.65%。
3) 比较CB513和25pdb两组可以发现,随着蛋白质数据量的增加,无论是贝叶斯分类器还是自动编码器,预测准确率得到了提高。
在本文的实验中,选取的是含单个隐含层的自动编码器来进行分类预测的,设置的稀疏度比较小,运行时间比较长。那么在接下来的实验中,首先进行参数的调整,降低运行时间。堆叠的自动编码器含有更多的隐含层,并且需要设置更多的隐含层神经元数。接下来我们会选取堆叠自动编码器来进行预测实验。
| [1] |
邵建林, 徐东, 王兰州, 等. 一种新的预测蛋白质二级结构的模型-贝叶斯神经网络[J]. 计量学报, 2006, 27(3): 281-285. SHAO Jianlin, XU Dong, WANG Lanzhou, et al. A new model for predicting protein two level structure-Bayesian neural network[J]. Metrology Journal, 2006, 27(3): 281-285. DOI:10.3321/j.issn:1000-1158.2006.03.020 (  0) 0) |
| [2] |
CHOU P Y, FASMAN G D. Prediction of protein conformation[J]. Biochemistry, 1974, 13(2): 222-245. DOI:10.1021/bi00699a002 (  0) 0) |
| [3] |
GARNIER J, OSGUTHORPE D J, ROBSON B. Analysis of the accuracy and implications of simple methods for predicting the secondary structure of globular proteins[J]. Journal of Molecular Biology, 1978, 120(1): 97-120. DOI:10.1016/0022-2836(78)90297-8 (  0) 0) |
| [4] |
QIAN N, SEJNOWSKI T J. Predicting the secondary structure of globular proteins using neural network models[J]. Journal of Molecular Biology, 1988, 202(4): 865-884. DOI:10.1016/0022-2836(88)90564-5 (  0) 0) |
| [5] |
吴玉明. 蛋白质二级结构预测的一种新的编码方式[J]. 工业控制计算机, 2015(4): 109-110, 113. WU Yuming. A new coding method for prediction of protein.secondary structure[J]. Industrial Control Computer, 2015(4): 109-110, 113. DOI:10.3969/j.issn.1001-182X.2015.04.048 (  0) 0) |
| [6] |
PATEL M S, MAZUMDAR H S. Knowledge base and neural network approach for protein secondary structure prediction[J]. Journal of Theoretical Biology, 2014, 361: 182-189. DOI:10.1016/j.jtbi.2014.08.005 (  0) 0) |
| [7] |
SPENCER M, EICKHOLT J, CHENG J. A Deep Learning Network Approach to ab initio Protein Secondary Structure Prediction[J]. IEEE/ACM Transactions on Computational Biology & Bioinformatics, 2015, 12(1): 103-112. DOI: 10.1109/TCBB.2014.2343960.
(  0) 0) |
| [8] |
ZAFER A, AJIT S, JEFF B. Learning sparse models for a dynamic Bayesian network classifier of protein secondary structure[J]. BMC Bioinformatics, 2011, 12(1): 154. DOI:10.1186/1471-2105-12-154 (  0) 0) |
| [9] |
王宝文, 王水星, 刘文远, 等. 结合支持向量机和贝叶斯方法进行蛋白质二级结构预测[J]. 生物信息学, 2010, 8(1): 75-77. WANG Baowen, WANG Shuixing, LIU Wenyuan, et al. Combining support vector machines and Bayesian methods to predict protein two structure prediction,[J]. Chinese Journal of Bioinformatics, 2010, 8(1): 75-77. DOI:10.3969/j.issn.1672-5565.2010.01.018 (  0) 0) |
| [10] |
吴琳琳, 徐硕. 基于SVM的蛋白质二级结构预测[J]. 生物信息学, 2010, 08(3): 187-190. Wu Linlin, XU Shuo. SVM based protein two class structure prediction[J]. Chinese Journal of Bioinformatics, 2010, 08(3): 187-190. DOI:10.3969/j.issn.1672-5565.2010.03.001 (  0) 0) |
| [11] |
WANG Y C, CHENG J Y, LIU Y H, et al. Prediction of Protein Secondary Structure using Support Vector Machine with PSSM Profiles——2016 IEEE Information Technology, Networking, Electronic and Automation Control Conference[C]. Chongqing: IEEE, 2016. 502-505. DOI: 10.1109/ITNEC.2016.7560411.
(  0) 0) |
| [12] |
泽瓦勒贝M (ZVELEBIL M)著. 李亦学, 郝沛主译理解生物信息学[M]. 北京: 科学出版社, 2012.
(  0) 0) |
| [13] |
KABSCH W, SANDER C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features[J]. Biopolymers, 1983, 22(12): 2577-2637. DOI:10.1002/bip.360221211 (  0) 0) |
| [14] |
张海霞, 唐焕文, 张立震, 等. 蛋白质二级结构预测方法的评价[J]. 计算机与应用化学, 2003, 20(6): 735-740. ZHANG Haixia, TANG Huanwen, ZHANG Lizhen, et al. Evaluation of protein two grade structure prediction method[J]. Computer and Applied Chemistry, 2003, 20(6): 735-740. DOI:10.3969/j.issn.1001-4160.2003.06.005 (  0) 0) |
| [15] |
张开旭, 周昌乐. 基于自动编码器的中文词汇特征无监督学习[J]. 中文信息学报, 2013, 27(5): 1-7, 92. ZHANG Kaixu, ZHOU Changle. Unsupervised feature Learning for chinese Lexion based on auto-encoder[J]. Journal of Chinese Information Processing, 2013, 27(5): 1-7, 92. DOI:10.3969/j.issn.1003-0077.2013.05.001 (  0) 0) |
| [16] |
RUMELHART D E, HINTON G E, EILLIAMS R J. Learning representations by back-propagating errors[J]. Readings in Cognitive Science, 1988, 323(6088): 399-421. DOI:10.1038/323533a0 (  0) 0) |
| [17] |
邓俊锋, 张晓龙. 基于自动编码器组合的深度学习优化方法[J]. 计算机应用, 2016, 36(3): 697-702. DENG Junfeng, ZHANG Xiaolong. Depth learning optimization method based on automatic encoder combination[J]. computer application, 2016, 36(3): 697-702. DOI:10.11772/j.issn.1001-9081.2016.03.697 (  0) 0) |
| [18] |
OLSHAUSEN B A, FIELD D J. Sparse Coding with an Overcomplete Basis Set: A Strategy Employed by V1?[J]. Vision Research, 1997, 37(23): 3311-3325. DOI:10.1016/S0042-6989(97)00169-7 (  0) 0) |
| [19] |
THEODORIDIS S, KOUTROUMBAS K. Pattern Recognition, Third Edition[J]. Encyclopedia of Information Systems, 2003, 459-479. DOI:10.1016/B0-12-227240-4/00132-5 (  0) 0) |
| [20] |
CUFF J A, BARTON G J. Application of multiple sequence alignment Profiles to improve protein secondary structure prediction[J]. Proteins: Structure, Function and Genetics, 2000, 40(3): 502-511. DOI:10.1002/1097-0134(20000815)40:33.0.CO (  0) 0) |
| [21] |
KEDARISETTI K D, KURGAN L A, DICK S. Classifier ensembles for protein structural class prediction with varying homology[J]. Biochemical Biophysical Research Communications, 2006, 348(3): 981-988. DOI:10.1016/j.bbrc.2006.07.141 (  0) 0) |
 2018, Vol. 16
2018, Vol. 16


