2. 温州商学院 信息工程学院,浙江 温州 325035
2. College of Information Engineering, Wenzhou Business College, Wenzhou 325035, Zhejiang, China
基于微阵列的高通量技术产生了大量的基因表达数据,如何从这些海量基因表达数据中获得洞察性的认识,进而理解生命现象的机制仍然是摆在世界各国科学家面前的一个严峻的挑战。生物通路是一组完成特定功能的基因之间的相互作用关系,主要有信号传导通路和代谢通路。在信号传导通路中,节点代表基因(或基因产物),边代表从一个基因转导到另一个基因的信号。在代谢通路中,节点代表生化化合物,边代表通过酶编码的化合物之间的生物化学反应,酶是为基因编码的。常用的通路数据库有KEGG[1]和Reactome[2]数据库,它们提供了基因之间相互作用的可视化形式。在过去十多年中,研究者开发了很多基于通路的基因表达差异分析方法,来识别各种癌症或疾病相关的通路。
2005年,PNAS上发表了两篇重要的通路分析方法的论文,一个是Tian等[3]提出的基于功能的显著通路分析方法,这种方法综合考虑了一个基因集合中基因表达与集合外基因表达差异的显著性(行置换),以及该基因集基因表达与表型相关性的的显著性(列置换)。另一个是Subramanian等[4]提出著名的基因集富集分析方法GSEA方法,其主要思想是根据通路中基因表达情况与给定表型之间的相关性对所有基因进行排序,然后确定给定通路P的Kolmogorov-Smirnov统计量在排序列表中靠近极端处程度的得分。该方法中,Kolmogorov-Smirnov统计量的显著性根据样本的列置换确定。2006年,Zahn等[5]使用Van der Waerden统计量代替Kolmogorov-Smirnov统计量并用自举抽样代替置换检验方法该方法考虑了通路中两个基因表达水平的相关性以及与其他因素的相关性。同年,EFRON等[6]用最大-均值统计量替代Kolmogorov-Smirnov统计量来计算通路分数,然后通过行置换方法对该分数进行标准化,最后利用列置换来检验通路分值的显著性,这就是著名的GSA方法。
从系统生物学的角度,基因之间的相互作用及其动力学的变化是导致各种疾病及癌症发生的主要原因[7-12]。因此,癌症相关通路的识别应尽可能考虑到通路中包含基因的各种信息,如基因的上下游位置、调控基因的数量、基因之间的作用关系等等因素。2009年,Tarca等[13]考虑了通路中基因的上下游位置关系提出了著名的信号通路影响分析(SPIA)方法。同年,Thomas等[14]提出了一种考虑通路中基因拓扑结构的方法,主要思想是位于上游和下游的基因比上下游中间位置具有更高权重,并且在打分上使得紧密连接的基因比不紧密连接的基因具有更高的分数。在通路中,有些基因频繁出现在很多通路中,这些基因可以看作是非特异性基因,其变化对特定通路的影响相对较小;反过来,另外一些基因仅在特定通路出现,即其特异性很高,这些基因的变化对该通路的影响往往很大。2012年,Tarca等[15]在GSA方法的基础上加入了基因特异性的影响,提出重叠基因降权的通路分析方法(PADOG)。最近,Liu等[14]提出了称为基因相互作用富集和网络分析(GIENA)的方法,以表示协同、竞争、冗余,表达水平的依赖性的失调的基因相互作用。
由KEGG中的Ras信号传导通路,可看出其中的Ras基因调节该通路中的许多下游基因。由于Ras基因参与控制细胞分裂和细胞死亡的许多信号传导通路,已有研究表明该基因的过表达和突变与许多癌症相关,如胰腺、结肠、肺(30%)、甲状腺、膀胱、卵巢、乳腺、皮肤、肝脏、肾脏和一些白血病等。显然在通路中,调控大量基因的基因应该比仅调控少量基因的基因更为重要,它们的差异对通路的功能应该具有更大的影响。考虑这一现象,本文将基因平均出度的大小定义为基因的重要性,并和PADOG方法中的基因的特异性结合起来,提出了一种基于重要性和特异性的通路识别方法PAGIS。在结肠癌、肺癌和胰腺癌3个数据集上的结果表明,改进后的方法能够提高癌症相关通路的识别精度。
1 材料与方法 1.1 数据集本文主要分析了3个癌症数据集。
1) 结肠癌数据集GSE4107,该数据集包括12个结肠癌样本与10个正常样本(Affymetrix HG-U133 Plus 2.0微阵列平台)。
2) 肺癌数据集GSE27262,该数据集包括25个肺癌样本和25个正常样本(Affymetrix Human Genome U133 Plus 2.0微阵列平台)。
3) 胰腺癌数据集GSE16515,包括36个胰腺癌样本和16个正常样本。
1.2 频度和平均出度的分布如图 1所示是KEGG数据库中204个信号通路的基因的频度和出度分布图,其中图 1(a)是基因的平均频度分布,可以看出大多数基因仅出现在一两条通路中,只有少数基因出现在多条通路中。图 1(b)是基因的平均出度分布,可以看出仅有少数基因调控大量下游基因,而大多数基因的平均出度在0~5之间。图 1(c)是基因的频度和平均出度的散点图,可以看出仅有部分平均出度大且频度低的基因。本文把平均出度在前100名的基因在DAVID数据库中进行GO功能注释,结果发现显著富集在一些癌症相关通路中,如pathways in cancer, adipocytokine signaling pathway, neurotrophin signaling pathway, thyroid cancer, ErbB signaling pathway, PPAR signaling pathway, 和renal cell carcinoma。这说明这些平均出度大的基因与癌症的发生发展具有密切的关系,提高它们在癌症相关通路中的权重具有生物学意义。

|
图 1 204条KEGG通路基因平均出度-频度分布图 Figure 1 Distribution of the average gene out-degrees and frequencies across the 204 KEGG signaling pathways |
基因在通路中出现的频度实际上反映了一个基因的特异性,频繁出现在很多通路中的基因属于一些“公共基因”,它们对通路的影响相对较小;仅在一条或几条通路中出现的基因其特异性高,它们的差异表达对通路的影响基因就大。在PADOG方法中,文献[15]定义基因的特异性权重为
| $ {w_f}\left( g \right) = 1 + \sqrt {\frac{{\max \left( f \right)-f\left( g \right)}}{{\max \left( f \right)-\min \left( f \right)}}} $ |
式中:max(f)、min(f)分别为204条KEGG通路中最大频度和最小频度;wf(g)反映基因在通路中特异程度,该值越大则基因在通路中特异程度越高,反之则特异程度越低,wf(g)取值在1~2之间。
由于基因出度表示的是一个基因调控的下游基因的数量,因此,出度越大的基因,对通路的影响就越大。为此,本文定义基因重要性的权重为
| $ {w_d}\left( g \right) = 1 + \sqrt {\frac{{d\left( g \right)-\min \left( d \right)}}{{\max \left( d \right)-\min \left( d \right)}}} $ |
式中:max(d)、min(d)分别为204条KEGG通路中基因最大平均出度和最小平均出度;wd(g)反映基因在通路中的重要性,该值越大则基因在通路中重要程度越高,值越小则基因在通路中重要程度越低,取值也在1~2之间。
1.3 癌症相关通路分析方法本文简要介绍GSEA方法、GSA方法、PADOG方法,进而引出本文的改进方法。假定所有基因总数为N,给定一个通路S,通路中基因数为M,GSEA的主要过程如下。
Step1 按照每个基因g与表型间相关性r(或t统计量)对N个基因排序wd(g)L=[g1, ..., gj, ...gN]。
Step2 用带权值的Kolmogorov-Smirnov统计量计算通路的富集分数ES0(S)为
| $ \begin{align} & \text{E}{{\text{S}}_{\text{0}}}\left( S \right)=\underset{1\le i\le N}{\mathop{\max }}\,\left| \sum\limits_{\begin{smallmatrix} {{g}_{j}}\in S \\ 1\le j\le i \end{smallmatrix}}{\left[ {{\left| {{r}_{j}} \right|}^{p}}/{{\sum\limits_{{{g}_{j}}\in S}{\left| {{\text{r}}_{j}} \right|}}^{p}} \right]}- \right. \\ & \left. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{\begin{smallmatrix} {{g}_{j}}\notin S \\ 1\le j\le i \end{smallmatrix}}{\frac{1}{N-M}} \right| \\ \end{align} $ |
式中p为用来校正ES的权值,p一般取1。
Step3 随机置换样本标签Nite次,并重新计算通路S的分数ESite(S)。
Step4 计算该通路富集分数ES0(S)的显著性p-value。
在GSA方法中,文献[6]使用“最大均值”统计量代替Kolmogorov-Smirnov统计量来计算通路分数ES。公式如下:
| $ {\rm{E}}{{\rm{S}}_{\rm{0}}}\left( S \right) = \max \left\{ {\frac{1}{M}\sum\limits_{{g_j} \in S} {z_j^{\left( + \right)}}, \left| {\frac{1}{M}\sum\limits_{{g_j} \in S} {z_j^{\left(-\right)}} } \right|} \right\} $ |
式中:
使用通路中所有基因的加权绝对矫正t分数和的均值来计算通路S分数ES0(S),公式如下:
| $ {\rm{E}}{{\rm{S}}_{\rm{0}}}\left( S \right) = \frac{1}{M}\sum\limits_{{g_j} \in S} {\left| {T\left( {{g_j}} \right)} \right|} \cdot {w_f}\left( {{g_j}} \right) $ |
式中:Τ(gj)为基因gj在两类样本中矫正t分数; wf(gj)为基因gj的权重。
利用行随机化和置换排列方法计算通路显著性p-value。公式如下:
| $ {P_{{\rm{PADOG}}}}\left( {ES} \right) = \frac{{\sum {_{{\rm{ite}}}I\left( {ES_{{\rm{ite}}}^*\left( S \right) \ge ES_0^*\left( S \right)} \right)} }}{{{N_{{\rm{ite}}}}}} $ |
式中:函数Ι中表达式为真则返回结果1,否则返回0;ESite*(S)为通路S在第ite次置换排列中的标准化得分。
1.5 基于基因重要性和特异性的通路分析方法(PAGIS)为将基因的平均出度引入到PADOG方法框架中,本文合并权重wf(g)和wd(g)成w(g),公式如下:
| $ w\left( g \right) = \sqrt {{w_f}\left( g \right) \cdot {w_d}\left( g \right)} $ |
式中:wf(g)为基因频度的权重;wd(g)为基因平均出度的权重;w(g)为合并权重且值取1~2;w(g)反映基因在通路中的重要性和特异性的程度,基因在通路中重要程度和特异程度越高则该值越大,相反基因的重要程度或特异程度越低则该值越小。本文将w(g)作为PADOG计算通路分数的新权重并提出PAGIS方法。
2 结果与分析本文比较PADOG和PAGIS方法在3个癌症数据集上的结果,PADOG的R语言包由文献[15]开发。由于不同方法p值计算有所不同,仅仅比较p值不够合理。本文基于通路的p值升序排列并比较排名,通路排名越靠前则该通路倾向被认为与癌症显著相关。表 1~3列出PADOG和PAGIS方法在前30名中与癌症相关的通路排名。在3个癌症数据集中,PADOG和PAGIS共识别出21、23、15条癌症相关通路。
| 表 1 PAGIS和PADOG方法在结肠癌数据集中前30名癌症相关通路和排名 Table 1 The rank of top 30 cancer-related pathway in colorectal cancer |
| 表 2 PAGIS和PADOG方法在肺癌数据集中前30名癌症相关通路和排名 Table 2 The rank of top 30 cancer-related pathway in lung cancer |
| 表 3 PAGIS和PADOG方法在胰腺癌数据集中前30名癌症相关通路和排名 Table 3 The rank of top 30 cancer-related pathway in pancreatic cancer |
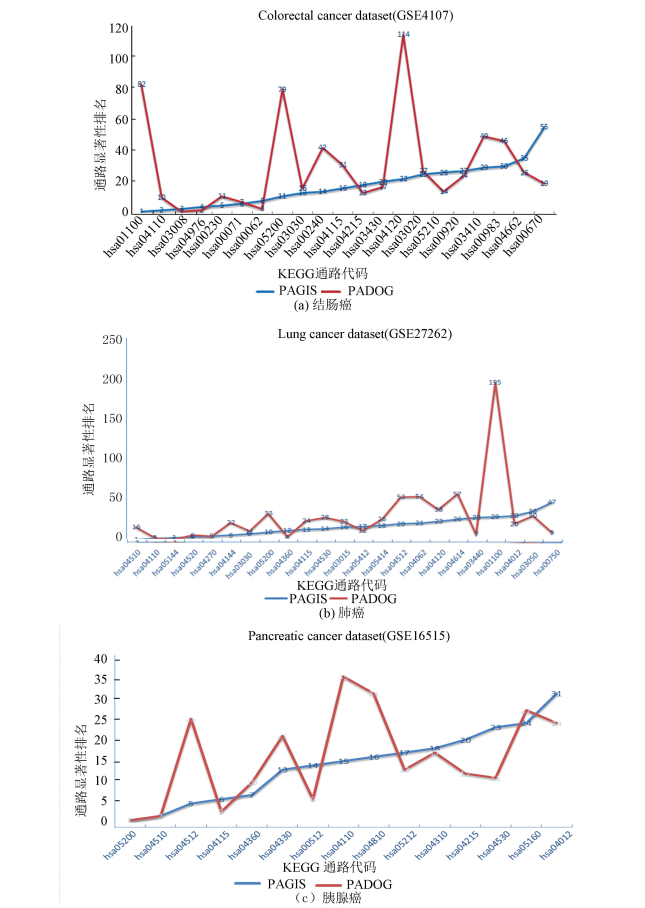
图 2(a)~(c)分别是PADOG和PAGIS方法在结肠癌、肺癌和胰腺癌数据集中癌症相关通路的排名折线图。该图中横轴对应表 1~3中Pathway No字段,纵轴对应表 1~3中PADOG和PAGIS方法中的通路排名。由图3可看出,相比PADOG方法PAGIS能够显著提高某些癌症相关通路的排名。如图 2(a)所示,通路Metabolic pathways, Pathways in cancer和Ubiquitin mediated proteolysis在PADOG方法中排名是82、79和114,而PAGIS是1、11和22;在肺癌数据集(图 2(b))中ECM-receptor interaction和Metabolic pathways在PADOG方法中排名分别是53、195,而PAGIS是20、29;在胰腺癌数据集中(图 2(c))中通路ECM-receptor interaction,Cell cycle和Regulation of actin cytoskeleton,在PADOG方法中排名分别是25、35和31, 而PAGIS是5、15和16。
|
图 2 PADOG和PAGIS方法在3个数据集中癌症相关通路排名折线图 Figure 2 Ranks of the cancer related pathways by PAGIS and PADOG in the three cancer datasets |
表 1~3列出PADOG和PAGIS方法在3个癌症数据集中识别出癌症相关通路的平均排名,PADOG方法识别出癌症相关通路的平均排名分别为30.14、29.43和15.87,而PAGIS分别为17.62、16.91和14.13,排名值越小越靠近排名列表的顶端位置,意味着总体与癌症相关程度越高;排名值越大越靠近排名列表的底端位置,意味着总体相关程度越低。显然在3个癌症数据集中PAGIS方法识别出的癌症相关通路平均排名位置比PADOG方法更靠近顶端位置。
另一方面如图 2中虚线所示,在结肠癌数据集中,排名在30名后的通路PADOG方法有7条,而PAGIS仅有2条;在肺癌数据集中PADOG方法有6条,PAGIS仅有2条;在胰腺癌数据集中PADOG方法有2条而PAGIS有1条。显然PAGIS方法能识别出更多的癌症相关通路。为进一步比较PADOG和PAGIS方法在3个癌症数据集中的性能,本文分别列出PADOG和PAGIS方法在前10、20和30名中识别出的癌症相关通路的数目,见表 4。表中在结肠癌数据集中前10名与癌症相关的通路PAGIS方法识别出7条,PADOG识别出5条,前20名中PAGIS方法识别出13条而PADOG识别出11条,前30名中PAGIS方法识别出19条而PADOG识别出14条。其他两个数据集的结果和结肠癌数据集类似,这说明在各段排名中PAGIS方法能稳定的识别出比PADOG更多的癌症相关通路,PAGIS具有比PADOG更好的性能优势。
| 表 4 PADOG和PAGIS方法在前10、20、30名中识别癌症相关通路数目 Table 4 Numbers of cancer-related pathway in top 10, 20, 30 identified by PADOG and PAGIS |
1) 本文统计了KEGG数据库中204条信号通路中基因的频度和出度,并计算出每个基因的平均出度。
2) 在基因特异性加权的通路分析方法(PADOG)基础上引入基因的平均出度,并用平均出度表示基因在通路中的重要程度。
3) 合并基因特异性和重要性的权值,提出一种基于基因拓扑重要性的通路识别方法(PAGIS), 并将该方法应用在结肠癌、肺癌和胰腺癌数据集中。
4) 总体上PAGIS方法比PADOG方法识别出更多的癌症相关通路,能稳定提高癌症相关通路的识别率。
| [1] |
KANEHISA M, FURUMICHI M, TANABE M, et al. KEGG: new perspectives on genomes, pathways, diseases and drugs[J]. Nucleic Acids Research, 2017, 45(D1): D353-D361. DOI:10.1093/nar/gkw1092 (  0) 0) |
| [2] |
FABREGAT A, SIDIROPOULOS K, VITERI G, et al. Reactome pathway analysis: a high-performance in-memory approach[J]. BMC Bioinformatics, 2017, 18(1): 142. DOI:10.1186/s12859-017-1559-2 (  0) 0) |
| [3] |
TIAN Lu, GREENBERG S A, KONG S W, et al. Discovering statistically significant pathways in expression profiling studies[J]. Proceedings of the National Academy of Sciences of the United States of America, 2005, 102(38): 13544-13549. DOI:10.1073/Pnas.0506577102 (  0) 0) |
| [4] |
SUBRAMANIAN A, TAMAYO P, MOOTHA V K, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles[J]. Proceedings of the National Academy of Sciences, 2005, 102(43): 15545-15550. DOI:10.1073/pnas.0506580102 (  0) 0) |
| [5] |
ZAHN J M, SONU R VOGEL H, et al. transcriptional profiling of aging in human muscle reveals a common aging signature[J]. PLoS Genetics, 2016, 2(7): e115. DOI:10.1371/journal.pgen.0020115 (  0) 0) |
| [6] |
EFRON B B, TIBSHIRANI R. On testing the significance of sets of genes[J]. The Annals of Applied Statistics, 2007, 1(1): 107-129. DOI:10.1214/07-AOAS101 (  0) 0) |
| [7] |
KHATRI P, SIROTA M, BUTTE A J. Ten years of pathway analysis: current approaches and outstanding challenges-supplementary notes[J]. Plos Computational Biology, 2012, 8(2): e1002375. DOI:10.1371/journal.pcbi.1002375 (  0) 0) |
| [8] |
TURNBULL C, SEAL S, RENWICK A, et al. Gene-gene interactions in breast cancer susceptibility[J]. Human Molecular Genetics, 2012, 21(4): 958-962. DOI:10.1093/hmg/ddr525 (  0) 0) |
| [9] |
JEONG H H, LEEM S, WEE K, et al. Integrative network analysis for survival-associated gene-gene interactions across multiple genomic profiles in ovarian cancer[J]. Journal of Ovarian Research, 2015, 8(1): 42. DOI:10.1186/s13048-015-0171-1 (  0) 0) |
| [10] |
ZHANG Jigang, LI Jian, DENG Hongwen. Identifying gene interaction enrichment for gene expression data[J]. Plos One, 2009, 4(11): e8064. DOI:10.1371/journal.pone.0008064 (  0) 0) |
| [11] |
DUTTA B, WALLQVIST A, REIFMAN J. PathNet: a tool for pathway analysis using topological information[J]. Source Code for Biology and Medicine, 2012, 7(1): 10. DOI:10.1186/1751-0473-7-10 (  0) 0) |
| [12] |
TARCA A L, DRAGHICI S, KHATRI P, et al. A novel signaling pathway impact analysis[J]. Bioinformatics, 2009, 25(1): 75-82. DOI:10.1093/bioinformatics/BTN577 (  0) 0) |
| [13] |
THOMAS R, GOHLKE J M, STOPPER G F, et al. Choosing the right path: enhancement of biologically relevant sets of genes or proteins using pathway structure[J]. Genome Biology, 2009, 10(4): R44. DOI:10.1186/gb-2009-10-4-r44 (  0) 0) |
| [14] |
TARCA A L, DRAGHICI S, BHATTI G, et al. Down-weighting overlapping genes improves gene set analysis[J]. BMC Bioinformatics, 2012, 13(1): 136. DOI:10.1186/1471-2105-13-136 (  0) 0) |
| [15] |
LIU Yu, KOYUTVRK M, BARNHOLTZ-SLOAN J S, et al. Gene interaction enrichment and network analysis to identify dysregulated pathways and their interactions in complex diseases[J]. BMC Systems Biology, 2012, 6(1): 65. DOI:10.1186/1752-0509-6-65 (  0) 0) |
 2017, Vol. 15
2017, Vol. 15


