2. 山东省肿瘤医院放疗病区, 济南 250117
2. Department of Radiation Oncology, Shandong Cancer Hospital, Jinan 250117, China
原发性肝癌[1-3]是全球第5大肿瘤疾病,中国原发性肝癌(primary liver carcinoma, PLC)患者众多,近年来精确放疗逐步成为治疗原发性肝癌的重要手段。2013年,黄伟等[4]采用logistic回归分析69例经精确放疗的PLC患者发现基线血清HBV DNA水平是影响HBV再激活的独立危险因素,精确放疗后导致患者发生乙型肝炎病毒(Hepatitis B virus, HBV)再激活率达25%,发生再激活的患者死亡率为25%,HBV再激活严重影响患者的生活质量以及生存周期。2014年,Huang等[5]又将临床剂量体积等因素纳入研究当中,发现NLV(正常肝体积),V20,和D-mean(平均剂量)与HBV再激活重要相关。2014年,汪孟森[6]对山东省肿瘤医院治疗的53例原发性肝癌患者进行研究,推测肝功能Child-Pugh分级可能是发生HBV再激活的危险因素。2015年,张晶晶等[7]研究发现HBV再激活患者和HBV未激活患者的Child-Pugh分级构成和HBV DNA水平差异具有统计学意义。吴冠朋等[8]对90例经精确放疗的原发性肝癌患者研究发现HBV DNA水平、外放边界和肿瘤分期TNM是致使HBV再激活的危险因素,并建立了基于BP和RBF神经网络的预测模型。随后Wu等[9]使用遗传算法应用在原发性肝癌患者精确放疗后的HBV再激活危险因素特征选择上,并建立了贝叶斯和支持向量机预测模型。临床上对原发性肝癌放疗后导致HBV再激活的危险因素有待进一步探究,且亟需建立更多的HBV再激活预测模型。
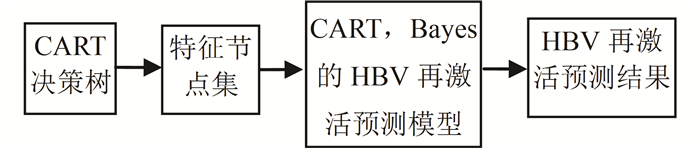
决策树算法包括CART、ID3、C4.5等, CART(classification and regression tree)算法是由Breiman等[10]提出的,是决策树中典型的二叉树,CART算法有着较强的模式识别能力,并广泛应用在复杂的生物数据分析中。陈磊等[11]将CART算法用在肺癌微阵列数据上,并得到优秀分类能力的CART树模型。Kong等[12]将CART算法用在乳腺癌分类上,提高了对乳腺癌的治疗质量。Gasparoviga-asite等[13]将CART算法用于降低蛋白质维度特征,并得到分类任务中最有效的特征子集。本文把划分CART树的特征节点集作为HBV再激活的危险因素,然后用这些特征节点集建立基于CART和Bayes的HBV预测模型,最后得到基于CART和Bayes的HBV再激活预测结果。实验设计流程如图 1所示。
|
图 1 实验设计流程 Figure 1 Experimental design process |
实验数据来自山东省肿瘤医院收治的90例经精确放疗的原发性肝癌患者的临床资料,数据包含:年龄、HBV DNA水平、外方边界、甲胎蛋白AFP和肿瘤分期TNM等28项特征属性,详见表 1。90例患者中20例发生了HBV再激活,HBV再激活率达22.22%。对本组数据研究的意义在于如何从这些数据中找出HBV再激活的危险因素,并建立HBV再激活预测模型,从而指导个体病人在治疗过程中采用抗病毒治疗方法,避免发生HBV再激活,提高病人的生存质量及延长病人的生存周期。
| 表 1 特征节点及其所代表的特征属性 Table 1 Feature nodes and their attributes |
CART[14]算法采用二分递归分割方法把数据中的特征作为二叉节点,CART算法可建立带有特征选择的分类树和回归树,本文用于判别HBV是否激活,因此本文建立的是带有特征选择的分类树。CART算法把非叶子结点作为判断类别的属性,叶子节点作为类别的标签, 定义数据样本集I,属性向量集X和类别向量集Y为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{I}} = \left( {\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Y}}} \right)\\ \mathit{\boldsymbol{X = }}\left( {{x_1}, {x_2}, \cdots, {x_m}} \right), \\ \mathit{\boldsymbol{Y = }}\left( {{y_1}, {y_2}, \cdots, {y_c}} \right). \end{array} \right. $ |
显然,本文数据中m=28,c=2。根据所给数据集I建立并划分一棵二叉树,CART算法使用GINI指数[15]划分一棵二叉树,对于一个c类样本集,用混合度impurity(P)来衡量节点的纯度(只包含同一类别的节点),GINI指数定义为
| $ {\rm{impurity}}\left( P \right) = {\rm{GINI}}\left( n \right) = 1-\sum\limits_1^c {{p^2}\left( c \right).} $ |
式中,P=(p1, p2, …, pc),其中p(c)为第c类的概率,则节点n的混合度为
| $ {\rm{impurity}}\left( P \right) = {\rm{impurity}}\left( {p_1 , {p_2}, \cdots, {p_c}} \right). $ |
当节点n是“纯”时GINI指数为0,否则为正。对CART树而言,当节点n不满足属于同一类别或只有一个样本时,就需要对节点n进行划分,而划分时将混合度最大的进行划分,则得到最优分支。当节点n被划分成n1和n2后,则有
| $ \left\{ \begin{array}{l} p\left( {{n_1}} \right) = \frac{{{N_{{n_1}}}}}{{{N_n}}}, \\ p\left( {{n_2}} \right) = \frac{{{N_{{n_2}}}}}{{{N_n}}}. \end{array} \right. $ |
式中:Nn1、Nn2、Nn分别为n1、n2、n的样本数,划分后的混合度Δimpurity(P)为
| $ \begin{array}{l} \Delta {\rm{impurity}}\left( P \right) = {\rm{impurity}}\left( P \right)-p\left( {{n_1}} \right) \cdot {\rm{GINI}}\left( {{n_1}} \right)-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;p\left( {{n_2}} \right) \cdot {\rm{GINI}}\left( {{n_2}} \right). \end{array} $ |
其他节点亦重复以上划分过程,当CART树遇见以下情况时,停止划分为:
1) 节点是纯的,即节点包含的样本属于同一类别。
2) 属性集已划分完毕。
3) CART树达到最大深度。
4) 每个节点已达到允许划分的最小记录数。
1.2.2 CART决策树的修剪CART决策树所选择的特征会影响预测结果,为了得到分类性能最好的CART树,对CART决策树的特征节点进行修剪,而修剪的方法包含前剪枝和后剪枝。前剪枝控制树的深度与叶子限制树的生长,后剪枝是在树完全生长后进行叶子与深度的再调整,较符合树的完全生长,本文以代价复杂性作为后修剪的策略,即
| $ {R_\alpha }\left( T \right) = E\left( T \right) + \alpha \left| {{N_T}} \right|. $ |
式中:Rα(T)为树T的代价复杂性;E(T)为树T的误分类损失;α为复杂性系数;|NT|为叶子节点树,以代价复杂性最小选择出剪枝子树。
1.3 Bayes分类模型Bayes[16]分类器是基于先验概率求后验概率的一种统计分类器。假定总体样本第i类样本的先验概率Pi,样品x属于i类样本的条件函数为fi(x),则
| $ {f_i}\left( x \right) = \left( {2\pi } \right)-\frac{e}{2}\left| {{\mathit{\boldsymbol{V}}_i}} \right|{\rm{-}}\frac{1}{2} \cdot {\rm{exp}}\left( {-\frac{{d_i^2\left( x \right)}}{2}} \right). $ |
式中:Vi为联合协方差矩阵;di2(x)为马氏距离,则基于Bayes理论判别x为i类样本的后验概率为
| $ P\left( {i|x} \right) = \frac{{{P_i}{f_i}\left( x \right)}}{{\sum {{P_i}{f_i}\left( x \right)} }}, i = 1, 2, \cdots, n. $ |
式中:Pi为第i个总体的先验概率;n为样本类别数量,显然本文中样本类别数量n为2。
1.4 Hold-out与K折交叉验证为保证选取的特征以及预测结果不失泛化性,先采用不同p的Hold-out选择出划分CART的特征节点集,本文的p分别设为:0.7、0.8、0.9。例如,本文90个原发性肝癌数据,则有90×p个数据用于划分CART的特征节点集,每次为不同p的Hold-out运行50次,特征节点集用于建立CART和Bayes预测模型,随后再采用K折交叉验证取预测结果的平均Ak,即
| $ {\bar A_K} = \frac{1}{K}\sum\limits_1^K {{A_K}, } $ |
式中,交叉验证的K设为10。
1.5 预测模型性能评估选用3个标准正确性(Accuracy)、灵敏性(Sensitivity)和特异性(Specificity)来评价所选特征的分类性能为:
| $ \begin{array}{l} {\rm{Accuracy = (}}TP{\rm{ + }}TN{\rm{)/}}(TP + TN + FP + FN){\rm{, }}\\ {\rm{Sensitivity = }}TP/(TP + FN{\rm{), }}\\ {\rm{Specificity = }}TN/(TN + FP{\rm{)}}{\rm{.}} \end{array} $ | (10) |
式中:Accuracy为综合预测结果,作为预测结果的主要评判标准;Sensitivity为再激活的预测结果;Specificity为正常的预测结果。TP、TN、FP、FN分别为真阳性(激活)、真阴性(正常)、假阳性和假阴性样本的数量。
2 结果与分析文献[9]的正确性已经达到82%以上,因此为了保证特征的意义,本文中预测结果选取正确性达到80%的特征节点集,且将正确性达到85%以上的特征节点集记为具有优秀的分类能力。
2.1 Hold-out的p为0.7时CART选择的特征节点集及CART预测结果运行了50次Hold-out(p为0.7)划分CART树所选择的特征节点集在10折交叉验证下的CART预测结果见表 2。
| 表 2 Hold-out的p为0.7时CART所选的特征节点集及CART预测结果 Table 2 The set of feature nodes selected by CART and the prediction result of CART are obtained when the p value of Hold-out is 0.7 |
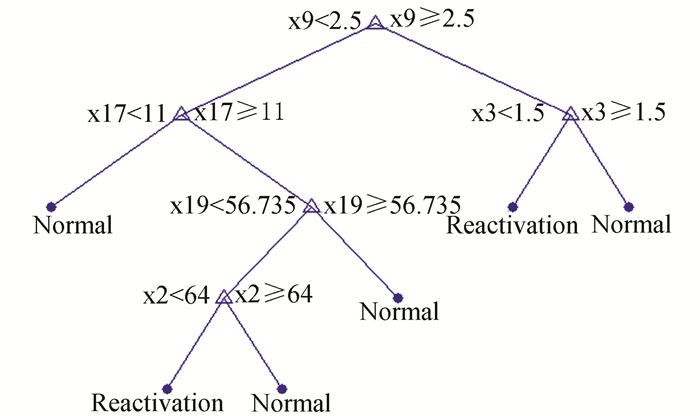
在CART的特征选择中,CART构建了易于理解的划分规则。例如表 2第1组特征节点集:HBV DNA水平(x9),外放边界(x17),KPS评分(x3),V10(x19)和年龄(x2)的分类规则如图 2所示,并最终得到激活(reactivation)和正常(normal)两种预测结果,其预测正确性达到87.55%,灵敏性更是高达98.49%,特异性达到77.61%。
|
图 2 特征节点集:HBV DNA水平(x9),外放边界(x17),KPS评分(x3),V10(x19)和年龄(x2)的分类规则 Figure 2 The classification rule of feature nodes set of HBV DNA Level(x9), outer margin of radiotherapy(x17), KPS score(x3), V10(x19) and Age(x2) |
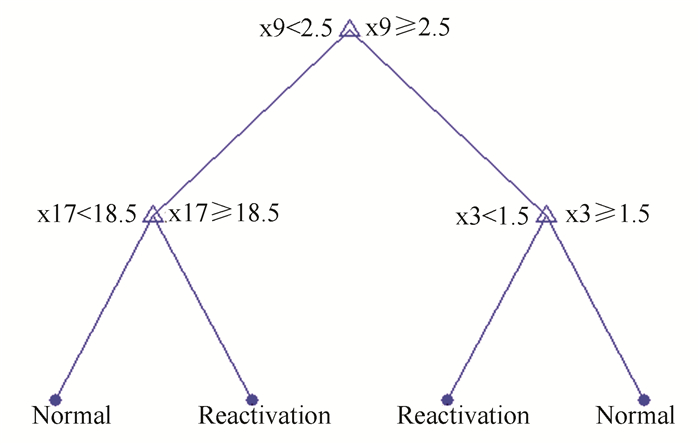
表 2第2组特征节点集:HBV DNA水平(x9),外放边界(x17)和KPS评分(x3)的正确性为85.16%,其分类规则如图 3所示。
表 2第3组特征节点集:HBV DNA水平,外放边界,V20和甲胎蛋白AFP的正确性为84.12%,表 2第4组特征节点集:HBV DNA水平,外放边界和V20已在文献[5]和文献[8]中证明是影响HBV再激活的危险因素,其正确性为83.18%,即“甲胎蛋白AFP”的加入增加了HBV再激活正确性。
|
图 3 特征节点集:HBV DNA水平(x9),外放边界(x17)和KPS评分(x3)的分类规则 Figure 3 The classification rule of feature nodes set of HBVDNA Level(x9), outer margin of radiotherapy(x17)and KPS score(x3) |
表 2第5组特征节点集:HBV DNA水平,外放边界和V10的正确性为81.31%。综合比较表 2中的正确性,显然特征节点“KPS评分”比特征节点“V20”和特征节点“V10”更能提高特征节点集的HBV再激活正确性,因此判定“KPS评分”是影响HBV再激活的危险因素,且存在对HBV再激活的正确性贡献度:KPS评分>V20>V10。
2.2 Hold-out的p为0.8时CART选择的特征节点集及CART预测结果运行50次Hold-out(p为0.8)划分CART树所选择的特征节点集在10折交叉验证下的CART平均预测结果见表 3。
| 表 3 Hold-out的p为0.8时CART所选的特征节点集及CART预测结果 Table 3 The set of feature nodes selected by CART and the prediction result of CART are obtained when the p value of Hold-out is 0.8 |
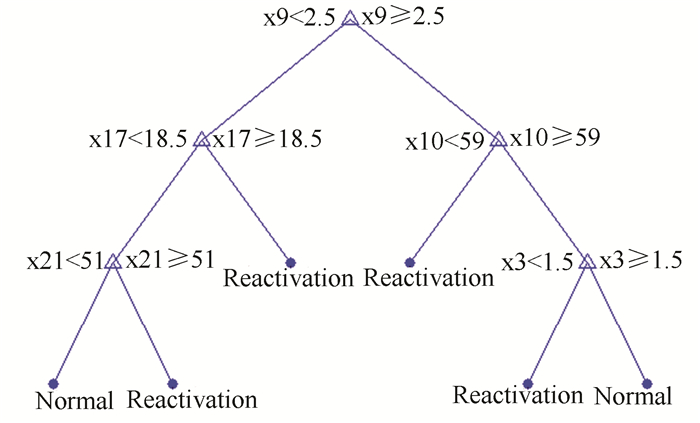
表 3第1组特征节点集:HBV DNA水平(x9),外放边界(x17),放疗总剂量(x10),V20(x21)和KPS评分(x3)的分类规则如图 4所示,其正确性为88.51%,灵敏性为97.74%,特异性为74.54%,该组特征节点集的正确性最好。
|
图 4 特征节点集:HBV DNA水平(x9),外放边界(x17),放疗总剂量(x10),V20(x21)和KPS评分(x3)的分类规则 Figure 4 The classification rule of feature nodes set of HBV DNA Level(x9), outer margin of radiotherapy(x17), total dose of radiotherapy(x10), V20(x21) and KPS score(x3) |
表 3第2组特征节点集:HBV DNA水平,外放边界,全肝最大剂量和甲胎蛋白AFP的分类正确性为86.73%,表明该特征节点集也具有优秀的分类能力。
表 3第3组特征节点集:HBV DNA水平,外放边界和全肝平均剂量的正确性为84.01%,高于表 2第4组特征节点集:HBV DNA水平,外放边界和V20的正确性,但低于表 2第2组特征节点集:HBV DNA水平,外放边界,KPS评分的正确性,即存在对HBV再激活的正确性贡献度:KPS评分>全肝平均剂量>V20。
2.3 Hold-out的p为0.9时CART选择的特征节点集及分类预测结果运行50次Hold-out(p为0.9)划分CART树所选择的特征节点集,特征节点集在10折交叉验证下的CART平均预测结果见表 4。
| 表 4 Hold-out的p为0.9时CART所选的特征节点集及CART预测结果 Table 4 The set of feature nodes selected by CART and the prediction result of CART are obtained when the p value of Hold-out is 0.9 |
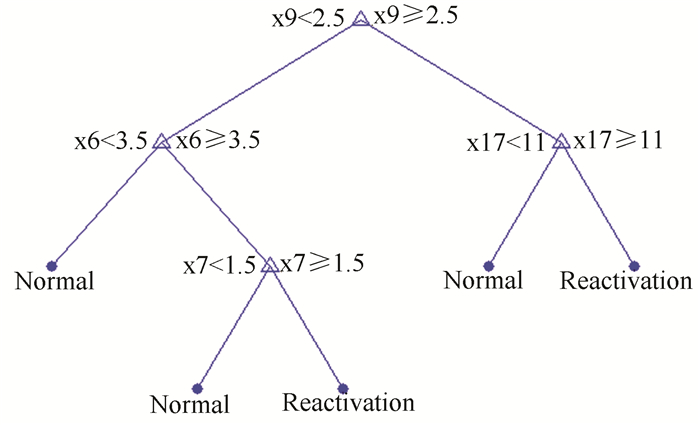
表 4第1组特征节点集:HBV DNA水平(x9),肿瘤分期TNM(x6),外放边界(x17),Child-Pugh(x7)的分类规则如图 5所示,其正确性为87.01%,灵敏性为97.95%,特异性为73.14%。
|
图 5 特征节点集:HBV DNA水平(x9),肿瘤分期TNM(x6),外放边界(x17),Child-Pugh(x7)的分类规则 Figure 5 The classification rule of feature nodes set of HBV DNA Level(x9), Tumor staging TNM(x6), outer margin of radiotherapy(x17), Child-Pugh(x7) |
表 4第2组特征节点集:HBV DNA水平,外放边界,肿瘤分期TNM和KPS评分的正确性为86.47%,表明该特征节点集也具有优秀的分类能力。
表 4第3组特征节点集:HBV DNA水平,外放边界和放疗总剂量的正确性为81.52%。低于表 2第4组特征节点集:HBV DNA水平,外放边界和V20的正确性,但高于表 2第5组特征节点集:HBV DNA水平,外放边界和V10的正确性,由此推出:对HBV再激活的正确性贡献度:V20>放疗总剂量>V10。
综上所述,得到一组对HBV再激活正确性贡献度的排序:KPS评分>全肝平均剂量>V20>放疗总剂量>V10。
2.4 特征节点集的Bayes预测模型结果Bayes不考虑所选特征节点的先后顺序,因此可用于判定某些特征节点的加入或者替换对HBV再激活的影响。其初始特征集和特征节点集的结果见表 5。
| 表 5 初始特征集和特征节点集的Bayes预测结果 Table 5 Bayes predictive results of original feature set and feature nodes set |
在表 5的Bayes预测模型中,特征节点集的分类性能相比初始特征集的都得到提高。但在相同特征节点集条件下,CART的分类性能略优于Bayes的分类性能。
表 5第1组特征节点集:HBV DNA水平,外放边界,放疗总剂量,V20和KPS评分在Bayes模型下的分类性能最好,正确性为86.69%,灵敏性为96.36%,特异性为74.86%,相比初始特征集其正确性,灵敏性和特异性分别提高:16.69%、21.36%和22.36%。并且该组特征节点集高于已知危险因素:HBV DNA水平,外放边界和V20的正确性、灵敏性和特异性。证明了特征节点“放疗总剂量”和“KPS评分”的加入提高了HBV再激活分类预测性能。
表 5第2组特征节点集:HBV DNA水平,外放边界,KPS评分,V10和年龄的正确性为86.51%。表 5第3组特征节点集:HBV DNA水平,肿瘤分期TNM,外放边界和Child-Pugh的正确性为85.65%。表 5第4组特征节点集:HBV DNA水平,外放边界,肿瘤分期TNM和KPS评分的正确性为84.95%。表 5中前4组特征节点集的正确性达到或接近85%,即认为是具有优秀分类能力的特征节点集。
表 5中第4、5组特征节点集中同时包含个特征节点:HBV DNA水平,外放边界和肿瘤分期TNM3时,Child-Pugh比KPS评分更能提升正确性,即存在对HBV再激活的正确性贡献度:Child-Pugh>KPS评分。
表 5第7组特征节点集含有“甲胎蛋白AFP”,其正确性略微高于没有“甲胎蛋白AFP”的第9组;第8组特征节点集也存在“甲胎蛋白AFP”,其正确性也略高于没有“甲胎蛋白AFP”的第10组,这证明了“甲胎蛋白AFP”增加了对HBV再激活正确性,与之前CART中的“甲胎蛋白AFP”增加了分类性能结论一致。
表 5中第6组特征节点集:HBV DNA水平,外放边界和KPS评分的正确性为84.24%;第9组特征节点集:HBV DNA水平,外放边界和全肝平均剂量的正确性为83.04%;第10组特征节点集:HBV DNA水平,外放边界和V20的正确性为82.74%;第11组特征节点集:HBV DNA水平,外放边界和放疗总剂量的正确性为80.95%;第12组特征节点集:HBV DNA水平,外放边界和V10的正确性为80.03%。由此推出对HBV再激活的正确性贡献度:KPS评分>全肝平均剂量>V20>放疗总剂量>V10,这与之前CART得出的正确性贡献度一致。
特征节点KPS评分越高则表明放疗后身体所能承受的副作用越强,致使HBV再激活的可能性越低,即预测结果表现为正常(Normal),反之为激活(Reactivation)。剂量参数V20、V10等代表了放疗与肝损伤的关系,V20、V10分别指接受20Gy或10Gy以上放疗的体积占全肝体积比例,放射性损伤不仅与受到的肝放射性耐受剂量存在着紧密联系, 而且与HBV再激活存在紧密联系。
对HBV再激活影响越大的危险因素被CART选作特征节点的可能性越大,实验中特征节点以及出现的次数见表 6。
| 表 6 特征节点与出现次数 Table 6 Feature nodes and the number of occurrences |
综上所述,不同特征节点集的分类性能不同,得到一个正确性较高的特征节点集:HBV DNA水平,外放边界,放疗总剂量,V20和KPS评分,并对实验中特征节点集的正确性比较后得到一组对HBV再激活正确性贡献度的排序:KPS评分>全肝平均剂量>V20>放疗总剂量>V10。特征节点“甲胎蛋白AFP”也增加了HBV再激活的正确性。已知的危险因素:HBV DNA水平和外放边界在所有CART特征节点中都出现,证明了CART算法特征选择的有效性。
3 结论1) 本文提出的CART算法应用在原发性肝癌患者精确放疗后致HBV再激活的特征节点集(危险因素)分析中,并建立了CART和Bayes预测模型。实验结果显示两种预测模型对原发性肝癌患者精确放疗后HBV再激活有着较强的模式判别能力,且CART的分类性能优于Bayes的分类性能。CART选择的特征节点集提高了HBV再激活分类性能,尤其特征节点集是:HBV DNA水平、外放边界、放疗总剂量、V20和KPS评分时的分类性能达到最优。经过实验结果的比较,得到了对HBV再激活正确性贡献度的排序:KPS评分>全肝平均剂量>V20>放疗总剂量>V10。“甲胎蛋白AFP”也会增加HBV再激活的正确性。已知的危险因素:HBV DNA水平和外放边界在所有CART特征节点中都出现,证明了CART算法特征选择的有效性。
2) CART的划分规则、特征节点的正确性贡献度、两种预测模型以及特征节点出现次数都可帮助医生对精确放疗的肝癌患者进行指导性治疗,并配合抗病毒和肝保护药物,防止HBV发生再激活,对提高患者的治疗效果,甚至防止HBV再激活导致的患者死亡具有重要意义。今后将继续研究其他特征选择方法和分类算法,致力于提高预测模型准确度。
| [1] |
EL-SERAG H B, RUDOLPH K L. Hepatocellular carcinoma: epidemiology and molecular carcinogenesis[J]. Gastroenterology, 2007, 132(7): 2557-2576. DOI:10.1053/j.gastro.2007.04.061 (  0) 0) |
| [2] |
JUNG J H, YOON S M, KIM S Y, et al. Radiation-induced liver disease after stereotactic body radiotherapy for small hepatocellular carcinoma: clinical and dose-volumetric parameters[J]. Radiation Oncology, 2013, 81(1): 1-7. DOI:10.1186/1748-717X-8-249 (  0) 0) |
| [3] |
叶胜龙. 2013年肝癌领域新进展[J]. 中华肝脏病杂志, 2014, 22(1): 2-4. YE Shenglong. New advances in liver cancer research: A review of 2013[J]. Chinese Journal of Hepatology, 2014, 22(1): 2-4. DOI:10.3760/cma.j.issn.1007-3418.2014.01.002 (  0) 0) |
| [4] |
黄伟, 卢彦达, 张炜, 等. 原发性肝癌精确放疗致乙型肝炎病毒再激活分析[J]. 中华放射肿瘤学杂志, 2013, 22(3): 193-196. HUANG Wei, LU Yanda, ZHANG Wei, et al. Analysis of hepatitis B virus reactivation induced by precise radiotherapy in patients with primary liver cancer[J]. Chinese Journal of Radiation Oncology, 2013, 22(3): 193-196. DOI:10.3760/cma.j.issn.1004-4221.2013.03.006 (  0) 0) |
| [5] |
HUANG Wei, ZHANG Wei, FAN Min, et al. Risk factors for hepatitis B virus reactivation after conformal radiotherapy in patients with hepatocellular carcinoma[J]. Cancer Science, 2014, 105(6): 697-703. DOI:10.1111/CAS.12400 (  0) 0) |
| [6] |
汪孟森. 原发性肝癌三维适形放疗致乙型肝炎病毒再激活相关研究[D]. 济南: 济南大学, 2014. WANG Mengsen.Reactivation of hepatitis B virus following three-dimensional conformal radiotherapy for primary hepatic carcinoma[D]. Jinan: University of Jinan, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10427-1014357710.htm (  0) 0) |
| [7] |
张晶晶, 曲颂, 余建荣, 等. 原发性肝癌三维适形放疗致乙型肝炎病毒再激活相关研究[J]. 癌症进展, 2015, 13(2): 183-187. ZHANG Jingjing, QU Song, YU Jianrong, et al. Related factors of reactivation of hepatitis B virus induced by three dimensional conformal radiotherapy in primary liver cancer[J]. Oncology Progress, 2015, 13(2): 183-187. DOI:10.11877/j.issn.1672-1535.2015.13.02.16 (  0) 0) |
| [8] |
吴冠朋, 王帅, 黄伟, 等. 基于BP神经网络的肝癌放疗致乙型肝炎病毒再激活分类预测模型[J]. 智能计算机与应用, 2016, 6(2): 43-47. WU Guanpeng, WANG Shuai, HUANG Wei, et al. Classification prognosis model of hepatitis B virus reactivation after radiotherapy in patients with primary liver carcinoma based on BP neural network[J]. Intelligent Computer and Applications, 2016, 6(2): 43-47. DOI:10.3969/j.issn.2095-2163.2016.02.014 (  0) 0) |
| [9] |
WU Guanpeng, LIU Yihui, WANG Shuai, et al. The classification prognosis models of hepatitis b virus reactivation based on Bayes and support vector machine after feature extraction of genetic algorithm[C]//Proceedings of the 12th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD). Changsha: IEEE, 2016: 572-577. DOI: 10.1109/FSKD.2016.7603236. http://ieeexplore.ieee.org/document/7603236/
(  0) 0) |
| [10] |
BREIMAN L I, FRIEDMAN J H, OLSHEN R A, et al. Classification and Regression Trees (CART)[J]. Biometrics, 1984, 40(3): 17-23. DOI:10.2307/2530946 (  0) 0) |
| [11] |
陈磊, 刘毅慧. 基于CART算法的肺癌微阵列数据的分类[J]. 生物信息学, 2011, 9(3): 229-234. CHEN Lei, LIU Yihui. Classification based on CART algorithm for microarray data of lung cancer[J]. China Journal of Bioinformatics, 2011, 9(3): 229-234. DOI:10.3969/j.issn1672-5565.2011.03.013 (  0) 0) |
| [12] |
KONG A L, PEZZIN L E, NATTINGER A B. Identifying patterns of breast cancer care provided at high-volume hospitals: a classification and regression tree analysis[J]. Breast Cancer Research & Treatment, 2015, 153(3): 689-698. DOI:10.1007/s10549-015-3561-6 (  0) 0) |
| [13] |
GASPAROVICA-ASITE M, POLAKA I, ALEKSEYEVA L. The impact of feature selection on the information held in bioinformatics data[J]. Information Technology & Management Science, 2016, 18(1): 115-121. (  0) 0) |
| [14] |
RICHETTE P, CLERSON P, BOUÉE S, et al. Identification of patients with gout: elaboration of a questionnaire for epidemiological studies[J]. Annals of the Rheumatic Diseases, 2014, 74(9): 1684-1690. DOI:10.1136/annrheumdis-2013-204976 (  0) 0) |
| [15] |
DAVIS M, ABRAMS M T, WISSOW L S, et al. Identifying young adults at risk of Medicaid enrollment lapses after inpatient mental health treatment[J]. Psychiatric Services, 2014, 65(4): 461-468. DOI:10.1176/appi.ps.201300199 (  0) 0) |
| [16] |
HOU Yi, EDARA P, SUN C. Modeling mandatory lane changing using bayes classifier and decision trees[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(2): 647-655. DOI:10.1109/TITS.2013.2285337 (  0) 0) |
 2017, Vol. 15
2017, Vol. 15


