2. 江苏省计算机信息处理技术重点实验室(苏州大学),苏州 215006
2. Provincial Key Laboratory for Computer Information Processing Technology of Jiangsu(Soochow University), Suzhou 215006, China
在最初的生物中心法则中,RNA被认为在表达遗传信息时作为蛋白质翻译,发挥了短暂的作用。后来发现RNA除了翻译蛋白质,还具有多种其他功能,如调控基因表达,转运RNA,催化肽链形成和指导蛋白质合成等。随着研究的深入,RNA的形象已经由功能单一的简单线性碱基序列演变成种类多样、结构复杂、功能特异的生命核心物,同时它在中心法则中取得了与DNA和蛋白质同样重要的地位。许多RNA序列具有准确定义的结构,想要理解这些RNA序列如何实现它们的功能,知道它们的结构是非常重要的[1]。
RNA中最基本的4种碱基为A(腺嘌呤)、U(尿嘧啶)、G(鸟嘌呤)、C(胞嘧啶)。RNA一级结构是碱基的有序序列。RNA二级结构是由碱基之间相互作用形成的3种规范碱基对AU,GC和GU以及未配对碱基的单链组成的结构[2]。RNA三级结构是原子的三维排列。因为RNA的结构一般是分层次的,所以二级结构可以在不用知道三级结构的情况下得到确定,同样也可以为预测三级结构提供很大的帮助。RNA二级结构承担着由RNA一级结构推测其三级结构的桥梁作用。研究RNA二级结构,可以为提高RNA及蛋白质结构预测的准确率提供帮助。因此,RNA结构研究的一个重要切入点是对其二级结构的研究。
鉴于二级结构的重要性,对二级结构的预测研究显得尤为重要。预测RNA二级结构的方法主要有序列比对法和最小自由能法。其中, 序列比对法需要耗费大量人力,预测效率较低,因而最小自由能法是预测RNA二级结构时广泛采用的一种方法。Zuker[3]提出的Mfold算法是早期基于最小自由能方法的二级结构预测算法,该算法有很高的正确率,但不能预测含假结的复杂结构。二级结构预测中,假结作为一种特殊的结构,是实现结构功能的重要因素。但是因为碱基相互重叠的特性,生物信息计算对假结的预测难以奏效。预测包含假结的RNA二级结构问题是NP难的[4],但要分析RNA的真实结构,对假结的准确预测是必须解决的问题。
通过加入假结约束来预测假结的最小自由能算法是目前使用比较多的预测方法,其中Probknot算法[5-6]在几种RNA含假结二级结构预测算法[7-10]中精准度较高。Probknot算法的配分函数(partition function)[11]利用机器学习法和热力学模型[12]计算出每个碱基之间的配对概率,各个碱基通过配对概率相互配对,然后解除形成的结构中连续配对碱基数较少的茎区,以确保稳定性[13],最终得出预测结果。本文运用多目标遗传算法,通过提高特异性从而提高总体精度的方式来改进Probknot算法,并与Probknot算法以及其他算法的结果进行对比和总结。
1 打分函数与预测性能指标 1.1 打分函数MaxExpect相比最小自由方法的最小自由能结构,MaxExpect利用RNA结构中各个碱基配对情况打分得到的最大期望精度结构比最小自由能结构具有更高的精度[14]。
MaxExpect的打分公式如下
| $ \begin{array}{l} {\rm{Expected accuracy}}\left( S \right) = \sum\limits_{i, j\in BP} { \in \gamma \cdot 2{P_{{\rm{bp}}}}\left( {i, j } \right) + } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{k \in SS} { \in {P_{ss}}\left( k \right)} \end{array} $ | (1) |
式中: γ取1; Pbp(ij)为碱基i与j相互配对的概率; Pss(k)为碱基k是单链的概率。ProbKnot算法中Pbp(i, j)是已知的,本文通过Pbp(i, j)计算出Pss(k)为
| $ {P_{ss}}\left( i \right) = 1-\sum\limits_{j = 1}^N {{P_{ij}}.} $ | (2) |
本文将以
预测性能指标是用来评价RNA二级结构预测结果好坏的标准。
马休兹相互作用系数(Matthews correlation coefficient, MCC)是通过比对天然结构与预测结构而计算出来的值,最小值为-1,表示预测结构与天然结构碱基配对相似度为0;最大值为1,表示预测结构与天然结构相似度为1。具体衡量公式如下:
| $ X = \frac{{{\rm{TP}}}}{{{\rm{TP + FN}}}}, $ | (3) |
| $ Y = \frac{{{\rm{TP}}}}{{{\rm{TP + FN}}}}, $ | (4) |
| $ {\rm{MCC}} = \frac{{{\rm{TP*TN-FP*FN}}}}{{\sqrt {\left( {{\rm{TP + FP}}} \right)\left( {{\rm{TP + FN}}} \right)\left( {{\rm{TN + FP}}} \right)\left( {{\rm{TN}} + {\rm{FN}}} \right)} }} $ | (5) |
式中:TP(true positive)为正确预测碱基对的个数;FN(false negative)为真实结构中存在但没有被正确预测出的碱基对个数;FP(false positive)为真实结构中不存在却被错误预测到的碱基对个数;TN(true negative)为正确预测的不配对的碱基的个数;敏感性X(sensitivity)指真实结构中所有的碱基对中被正确预测到的百分比;特异性Y(specificity)指在所有预测到的碱基对中正确预测的百分比。
在评价RNA二级结构预测的结果时,如果天然结构中i与j配对,那么预测结构中除了i与j配对,i与j+1或j-1以及j与i-1或i+1配对都被认为是正确的配对,这是考虑到了多种因素,包括确定确切配对的困难性,以及这些预测的配对在质量上与正确配对的一致性[15]。
2 多目标遗传算法 2.1 多目标优化问题多目标优化问题的关键点在于如何使各个目标之间同时达到最优[16-17]。多目标优化问题的解不仅仅是一个全局最优解,而是一个解集,本文称这个解集为Pareto最优解集[18]。在这个解集中彼此任意解都不相互支配,并且解集外的解都会被解集中至少一个解支配。
遗传算法是一种可用于寻找最优解的搜索算法,它借鉴了生物界的进化规律,通过模拟自然进化过程以此来搜索最优解。由于遗传算法运行一次能找到多目标优化问题的多个Pareto最优解,因而它是求解多目标优化问题的一个有效手段[19]。
NSGA-Ⅱ是目前多目标优化领域中最优秀的多目标遗传算法之一,它被国内外学者广泛引用,本文将主要结合该算法的思想来进行实验。
2.2 NSGA-ⅡNSGA-Ⅱ(Non-dominated sorting genetic algorithm)是一种新型多目标优化遗传算法,相对于NSGA的缺陷,NSGA-Ⅱ有如下改进:计算复杂性从O(mN3)降至O(mN2),具备最优保留机制及无需确定一个共享参数的优点,从而进一步提高计算效率和算法的鲁棒性。NSGA-Ⅱ该算法求得的Pareto最优解分布均匀,收敛性和鲁棒性好,具有良好的优化效果,是求解多目标优化问题的一种新思路[20-23]。
NSGA-Ⅱ的遗传算法中,通过适应度函数计算每个个体的适应度并对其进行排序,排序算法分为两个步骤。
Step 1 Non-dominated sorting(非支配排序).种群基于Pareto顺序分为k个子集(Q1, …, Qk),每个Qi中的个体都不会被Qj中的个体支配(i<j)。
Step 2 Crowding-distance sorting(拥挤距离排序).子群Qi用拥挤距离排序。在不拥挤局域内的解优先度更高。
2.2.1 非支配排序快速非支配排序是基于非支配排序的改进算法见表 1。
| 表 1 快速非支配排序 Table 1 Rapid non dominated sorting |
非支配排序。m个个体和种群中的其他个体进行支配关系比较,是否支配其他全部个体,复杂度为O(mN);循环进行直到等级1中的非支配个体全部被搜索到,复杂度为O(mN2);最坏的情况下,有N个等级,每个等级只存在一个解,复杂度为O(mN3)。
2.2.2 拥挤距离排序拥挤距离排序用于保持解的多样性。每个个体的拥挤距离是通过计算与其相邻的两个个体在每个子目标函数上的距离差之和来求取, 如图 1所示。
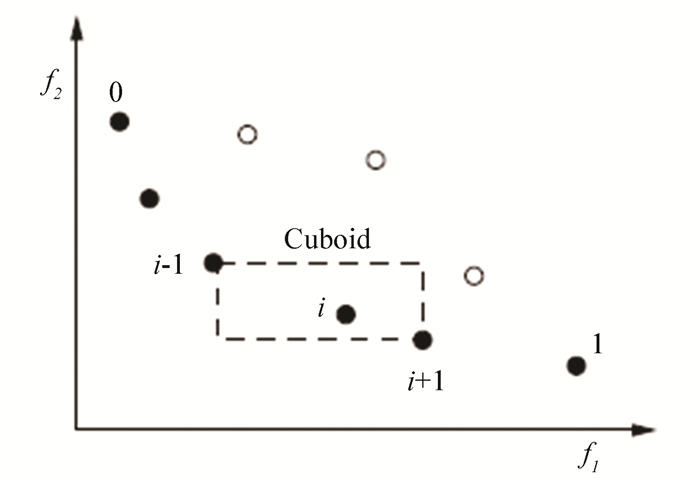
|
图 1 二目标函数的拥挤距离计算 Figure 1 The crowding distance calculation of two objective functions |
图 1所示个体i的拥挤距离为
| $ {D_i}{\rm{ = }}\left( {{f_{i + 1, 1}}-{f_{i-1, 1}}} \right) + \left( {{f_{i-1, 2}} - {f_{i + 1, 2}}} \right), $ | (6) |
即图 1中虚线四边形的长与宽之和。
排序时当两个个体属于不同等级的非支配解集时,等级较小的优先度高,当两个个体属于相同等级的非支配解集时,拥挤距离较大的优先度高, 即
| $ \begin{array}{l} \;\;{\rm{if}}\left( {{i_{{\rm{rank}}}} < {j_{{\rm{rank}}}}} \right){\rm{or}}\left( {\left( {{i_{{\rm{rank}}}} = {j_{{\rm{rank}}}}} \right){\rm{and}}\left( {{i_{{\rm{distance}}}} < {j_{{\rm{distance}}}}} \right)} \right)\\ {\rm{the}}\left( {i{ \ge _n}j} \right) \end{array} $ |
NSGA-Ⅱ中遗传算法流程如图 2所示。
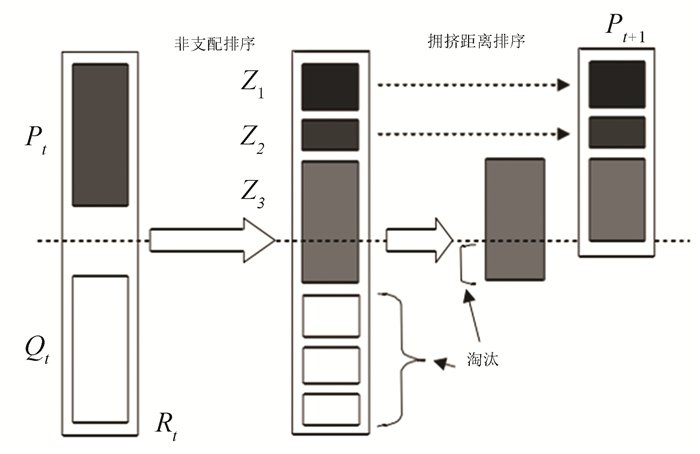
|
图 2 NSGA-Ⅱ步骤 Figure 2 Steps of NSGA-Ⅱ |
Step 1 创造一个初始父代种群P0,使用交叉和变异操作产生子代种群Q0。
Step 2 对P0和Q0组成的整体R0进行非支配排序,构造所有不同等级的非支配解集Z1, Z2, Z3, ……。
Step 3 对分好等级的非支配解集进行拥挤距离排序,根据适应度高低得到前N个解,构成下一次迭代的父代种群P1。
Step 4 重复上述3个步骤,直到结果收敛。
3 数据与实验流程 3.1 数据集本文采用ASE以及CRW的RNA数据集作为实验的研究对象,对ASE与CRW的RNA天然结构进行计算,提取出每个RNA结构的一级序列,通过ProbKnot算法的配分函数,得到包含碱基配对概率的pfs文件,将此文件作为本文输入。经过计算,有效的数据集为877个。其中ASE案例450个,CRW案例427个(见表 2)。ASE的序列长度大多数在200~500之间,CRW的序列长度大多数在1 000以上。
| 表 2 实验数据集表 Table 2 The experimental dataset |
基于多目标遗传算法的含假结RNA二级结构预测方法,实验过程如下。
Step1 首先通过对单个RNA序列进行变异算法得到不同的RNA二级结构作为遗传算法的初始种群,然后通过对初始种群内的个体进行变异交叉算法形成数量相同的新的RNA二级结构,再对每个RNA二级结构进行适应度计算排序,选择适应度较高的个体组成新的种群。
Step2 重复该步骤直到结果收敛,将种群中的最优个体作为结果输出,得到这个RNA序列的二级结构预测结果。
Step3 输入其他每个RNA序列来完成上述两个步骤,得到所有RNA序列的二级结构预测结果,作为实验结果。其中,为了适应遗传算法中的交叉与变异,算法对RNA二级结构采用如图 3所示的精英保留策略。图 3中,位于上方的结构(a)表示1号和4号碱基配对、2号和3号碱基为单链的RNA二级结构,它通过变异算法可能形成结构(b)与结构(c)。同样的,位于下方的结构(a)与结构(b)通过交叉算法可能形成结构(c)与结构(d)。
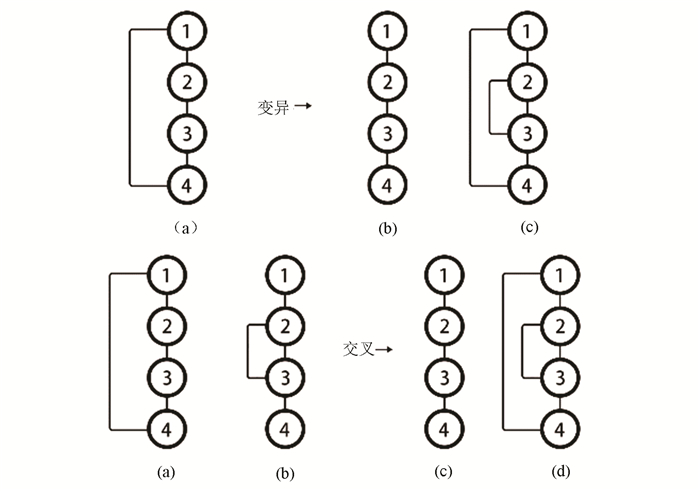
|
图 3 RNA二级结构的交叉和变异 Figure 3 Crossing and mutating of RNA secondary structure |
实验的参数设置会对实验结果产生影响。本次实验中有4个参数对实验结果影响较大,它们是populations,iterations,minloop与α,其中:Populations是初始种群数,iterations是收敛后迭代次数。这两个参数值设置的越大,遗传算法搜索到最优解的可能性越高,但运行时间也会越长。根据RNA序列的长度大小,本次实验populations的取值为1 000~2 000。由于RNA序列长度与种群数的区别,不同的结构使用遗传算法的迭代次数相差较大,所以iterations表示收敛后的迭代次数而不是总迭代次数,它的取值为500~1 000。
Minloop是最小螺旋长度,α是用于比较配对概率与单链概率的一个数值。为了提高交叉变异算法的效率,算法对形成的结构进行了两方面的约束:一是在每次交叉变异形成RNA二级结构后,算法会去除长度小于minloop的螺旋来保证RNA结构的稳定性,因为天然结构中螺旋长度小于3的结构较为少见,所以minloop取值为3;二是在交叉变异时,只进行概率大于α的配对与解除配对,这样可以减少结构中配对概率与单链概率为0或很小的碱基对与单链,避免采用完全随机交叉变异会消耗大量不必要资源的情况,α取值为0.001~0.1,这个值越大,算法收敛速度越快,但会降低结果的多样性。
4 结果与分析 4.1 多目标遗传算法与ProbKnot算法结果对比在877个实验结果中,有9个案例(其中ASE案例2个,CRW案例7个)的敏感性和特异性在两种算法的计算下都为0,因此之后的数据统计中删除了这9个案例。
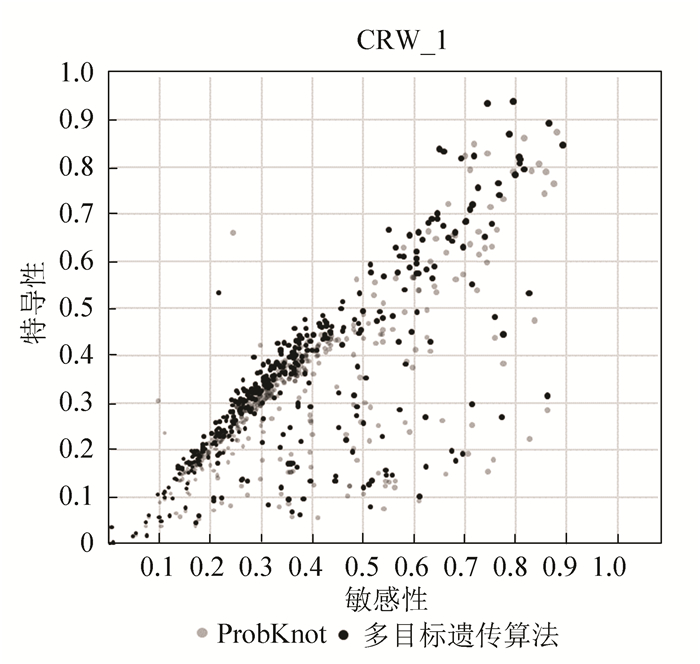
图 4、5比较了实验案例的敏感性与特异性,多目标遗传算法的结果用黑色的点表示,Probknot算法的结果用灰色的点表示,点所在的位置越是接近右上,结果越好。图 4、5中表明, 单从敏感性与特异性的结果上看,多目标遗传算法的优势并不明显。
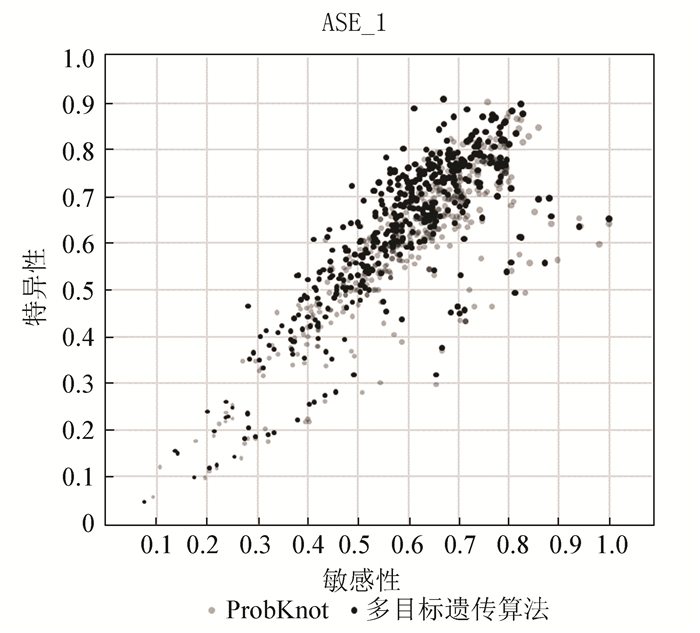
|
图 4 448个ASE案例敏感性与特异性值统计 Figure 4 The statistic of sensitivity and specificity about 448 cases of ASE |
|
图 5 420个CRW案例敏感性与特异性值统计 Figure 5 The statistic of sensitivity and specificity about 420 cases of CRW |
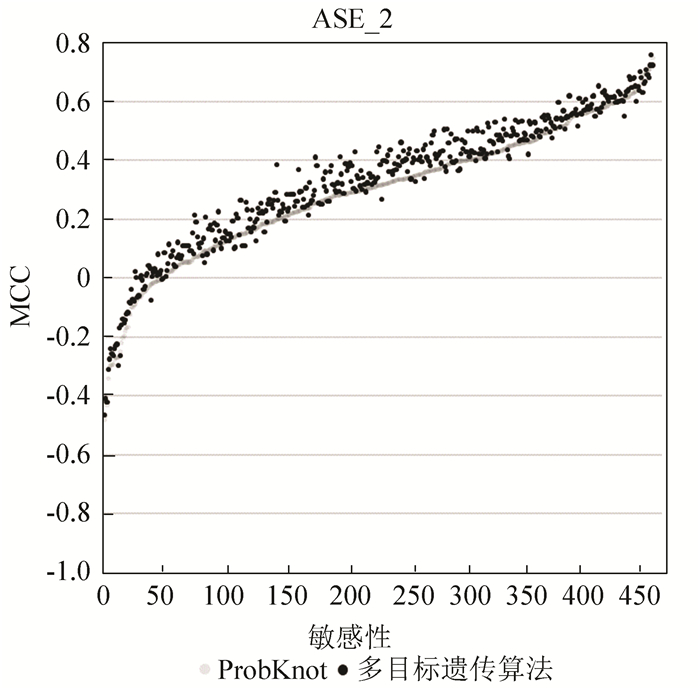
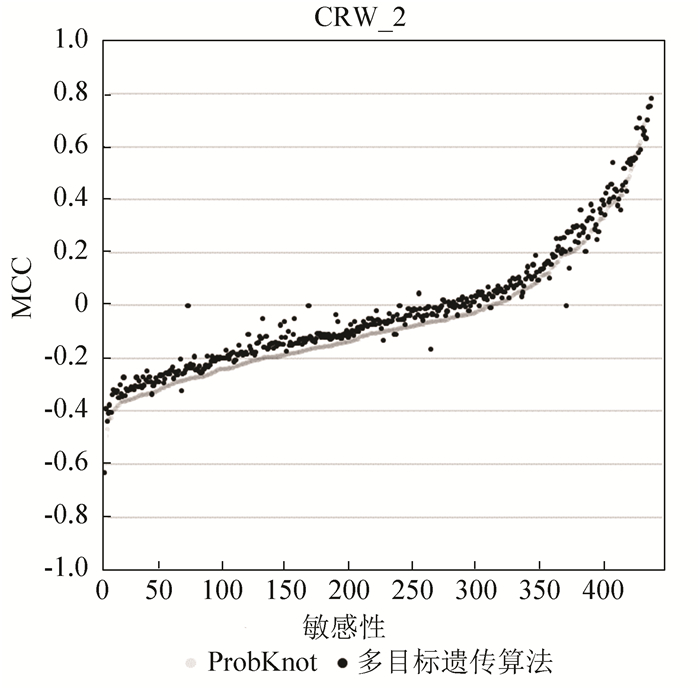
MCC值是综合敏感性与特异性的评价指标,如图 6、7所示。多目标遗传算法的结果用黑色的点表示,Probknot算法的结果用灰色的点表示,点所在的位置越是接近上方,结果越好。从图 6、7中可以看出,大多数黑色的点在灰色点的上方,这意味着在大多数实验案例上,多目标遗传算法的结果优于Probknot算法。
|
图 6 448个ASE案例MCC值统计 Figure 6 The statistic of MCC about 448 cases of ASE |
|
图 7 420个CRW案例MCC值统计 Figure 7 The statistic of MCC about 420 cases of CRW |
表 3整理了ProbKnot算法和多目标遗传算法的实验数据的平均值。表 3中数据表明,多目标遗传算法在ASE和CRW数据集上有更高的特异性与MCC值。
| 表 3 RNA二级结构预测方法实验对比表 Table 3 Comparison of methods for predicting RNA secondary structure |
本文选取了263个案例(其中ASE案例158个,CRW案例105个),采用ProbKnot算法、多目标遗传算法、MaxExpect算法、Fold算法[24]进行对比实验。
表 4整理了ProbKnot算法、多目标遗传算法、MaxExpect算法、Fold算法的实验数据的平均值。表 4中数据表明, 4种RNA二级结构预测方法中,多目标遗传算法在ASE和CRW数据集上有更高的特异性与MCC值,在CRW数据集上的特异性也较高。
| 表 4 4种RNA二级结构预测方法实验对比 Table 4 Comparison of four methods for predicting RNA secondary structure |
由于CRW数据集中RNA序列长度相差较大,第2次对比实验选取了一些长度较短的案例,表 3中CRW数据集的总体精度比表 2要高。
4.3 实验小结两次对比实验中,多目标遗传算法在ASE和CRW数据集上的特异性与MCC的平均值更高,大多数案例在改进算法后MCC值得到提高,敏感性提升不明显。因此本文可以得出结论,多目标遗传算法的精度更高,得到的结果与天然结构更接近。
5 结论1) 本文基于多目标遗传算法,使用概率模型进行RNA二级结构打分,在多目标优化部分计算出碱基的单链概率,以此完善概率模型。在遗传算法部分根据RNA二级结构的特征编写适合的交叉变异算法,以此提高程序运行效率。
2) 实验结果表明,在ASE和CRW数据集上的对比试验中,多目标遗传算法的精度更高,相比ProbKnot算法,MCC值平均提高4%。
3) 本文运用多目标优化算法对假结RNA二级结构进行了实验预测,证明了多目标遗传算法可以有效地增加含假结RNA二级结构预测的精度,但仍然具有发展和改进的空间。
| [1] |
WAN Yue, QU Kun, ZHANG Qiangfeng, et al. Landscape and variation of RNA secondary structure across the human transcriptome[J]. Nature, 2014, 505(7485): 706-709. DOI:10.1038/nature12946 (  0) 0) |
| [2] |
PENALVA L O F. RNA secondary structure[M]. New York: Encyclopedia of Systems Biology, 2013, 1864-1864. DOI:10.1007/978-1-4419-9863-7_319
(  0) 0) |
| [3] |
ZUKER M. Mfold web server for nucleic acid folding and hybridization prediction[J]. Nucleic acids research, 2003, 31(13): 3406-3415. DOI:10.1093/nar/gkg595 (  0) 0) |
| [4] |
RUAN Jianhua, STORMO G D, ZHANG Weixiong. An iterated loop matching approach to the prediction of RNA secondary structures with pseudoknots[J]. Bioinformatics, 2004, 20(1): 58-66. DOI:10.1093/bioinformatics/btg373 (  0) 0) |
| [5] |
MATHEWS D H, DISNEY M D, CHILDS J L, et al. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(19): 7287-7292. DOI:10.1073/pnas.0401799101 (  0) 0) |
| [6] |
BELLAOUSOV S, MATHEWS D H. ProbKnot: fast prediction of RNA secondary structure including pseudoknots[J]. Rna, 2010, 16(10): 1870-1880. DOI:10.1261/rna.2125310 (  0) 0) |
| [7] |
BINDEWALD E, KLUTH T, SHAPIRO B A. CyloFold: secondary structure prediction including pseudoknots[J]. Nucleic Acids Research, 2010, 38(suppl_2): W368-W372. DOI:10.1093/nar/gkq432 (  0) 0) |
| [8] |
SATO K, KATO Y, HAMADA M, et al. IPknot: fast and accurate prediction of RNA secondary structures with pseudoknots using integer programming[J]. Bioinformatics, 2011, 27(13): i85-i93. DOI:10.1093/bioinformatics/btr215 (  0) 0) |
| [9] |
JABBARI H, CONDON A. A fast and robust iterative algorithm for prediction of RNA pseudoknotted secondary structures[J]. BMC Bioinformatics, 2014, 15: 147. DOI:10.1186/1471-2105-15-147 (  0) 0) |
| [10] |
DAWSON W K, TAKAI T, ITO N, et al. A new entropy model for RNA: part Ⅲ. Is the folding free energy landscape of RNA funnel shaped?[J]. Journal of Nucleic Acids Investigation, 2014, 5: 2652. DOI:10.4081/jnai.2014.2652 (  0) 0) |
| [11] |
MATHEWS D H. Using an RNA secondary structure partition function to determine confidence in base pairs predicted by free energy minimization[J]. Rna, 2004, 10(8): 1178-1190. DOI:10.1261/rna.7650904 (  0) 0) |
| [12] |
SEETIN M G, MATHEWS D H. TurboKnot: rapid prediction of conserved RNA secondary structures including pseudoknots[J]. Bioinformatics, 2012, 28(6): 792-798. DOI:10.1093/bioinformatics/bts044 (  0) 0) |
| [13] |
YONEMOTO H, ASAI K, HAMADA M. A semi-supervised learning approach for RNA secondary structure prediction[J]. Computational Biology and Chemistry, 2015, 57: 72-79. DOI:10.1016/j.compbiolchem.2015.02.002 (  0) 0) |
| [14] |
LU Z J, GLOOR J W, MATHEWS D H. Improved RNA secondary structure prediction by maximizing expected pair accuracy[J]. Rna, 2009, 15(10): 1805-1813. DOI:10.1261/rna.1643609 (  0) 0) |
| [15] |
DEIGAN K E, LI T W, MATHEWS D H, et al. Accurate SHAPE-directed RNA structure determination[J]. Proceedings of the National Academy of Sciences, 2009, 106(1): 97-102. DOI:10.1073/pnas.0806929106 (  0) 0) |
| [16] |
DEB K. Multi-objective optimization[M]. Springer US: Search Methodologies, 2014, 403-449.
(  0) 0) |
| [17] |
DEB K. Multi-objective optimization using evolutionary algorithms[M]. New York, NY: John Wiley & Sons, 2001, 3-34. DOI:10.1007/978-0-85729-652-8_1
(  0) 0) |
| [18] |
ARNOLD B C. Pareto distribution[M]. New York, NY: John Wiley & Sons, Ltd, 2015. DOI:10.1002/9781118445112.stat01100.pub2
(  0) 0) |
| [19] |
LI Hui, ZHANG Qingfu. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 284-302. DOI:10.1109/TEVC.2008.925798 (  0) 0) |
| [20] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 (  0) 0) |
| [21] |
DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-Ⅱ[C]//International Conference on Parallel Problem Solving From Nature. Berlin Heidelberg: Springer, 2000: 849-858. DOI: 10.1007/3-540-45356-3_83.
(  0) 0) |
| [22] |
DEB K, JAIN H. Handling many-objective problems using an improved NSGA-Ⅱ procedure[C]//2012 IEEE Congress on Evolutionary Computation. Brisbane, QLD, Australia: IEEE, 2012: 1-8.DOI: 10.1109/CEC.2012.6256519
(  0) 0) |
| [23] |
SEADA H, DEB K. U-nsga-Ⅲ: A unified evolutionary optimization procedure for single, multiple, and many objectives: Proof-of-principle results[C]//International Conference on Evolutionary Multi-Criterion Optimization. Cham: Springer, 2015: 34-49. DOI: 10.1007/978-3-319-15892-1_3.
(  0) 0) |
| [24] |
BELLAOUSOV S, REUTER J S, SEETIN M G, et al. RNAstructure: Web servers for RNA secondary structure prediction and analysis[J]. Nucleic acids research, 2013, 41: W471-W474. DOI:10.1093/nar/gkt290 (  0) 0) |
 2017, Vol. 15
2017, Vol. 15


