肌肉在周期的收缩或静态的拉伸过程中,会逐渐进入疲劳状态[1]。如何有效地判别肌肉疲劳,对于进一步的治疗及疗效评价具有重要的方法和意义[2]。当肌肉持续收缩一段时间时,引起肌肉生理特性改变,表现为兴奋性、传导性和收缩性的降低,并引起肌肉物理展长性和弹性减弱,肌肉变得不能够产生所需要的力,这种现象称为肌肉疲劳[3]。疲劳时的肌肉收缩幅度明显降低[4]。
本文从时域和频域、时频域线性方法下的测量指标和非线性方法下的指标来综述表面肌电信号的疲劳研究进展,同时比较各种方法的优缺点,并对使用表面肌电信号来判别疲劳研究做了进一步的展望。
1 时域指标和频域指标下疲劳判别 1.1 时域分析下的疲劳判别时域分析将肌电信号看作时间的函数,通常分析信号的均值、幅值直方图等指标来反映信号振幅在时间维度的变化。通常使用的指标有电活动水平(electrical activity, EA)、过零率(zero crossing rate, ZCR)、平均整流值(average rectified value, ARV)、积分肌电值(integrated electromyogram, iEMG)和均方根值(root mean square, RMS)其中EA是指原始信号经过低通滤波及平滑修正后对特定长度时间窗口的振幅进行平均而得来,而过零率反映信号在单位时间内的过零次数; ARV、iEMG和RMS通过如下公式计算得到:
| $ \begin{array}{l} {\rm{ARV}} = 1/T\smallint _{_t}^{^{t + T}}|{\rm{EMG}}\left( t \right)|{\rm{d}}t, \\ {\rm{iEMG}} = \smallint _{_t}^{^{t + T}}|{\rm{EMG}}\left( t \right)|{\rm{d}}t, \\ {\rm{RMS}} = \sqrt {1/T\smallint _{_t}^{^{t + T}}{\rm{EM}}{{\rm{G}}^2}\left( t \right){\rm{d}}t} . \end{array} $ |
Inbar等[5]的研究表明过零率与表面肌电信号(surface electromyography, sEMG)的平均频率和中值频率有很好的相关性,过零率的降低表示疲劳的发生。Jukka等[6]让受试者保持等距60%最大随意收缩的膝关节伸直,随后进行参数分析,发现疲劳期受试者的积分肌电值(iEMG)轻微但持续的上升。Madeleine等[7]在做疲劳和非疲劳间的上斜方肌表面肌电实现时,疲劳期间ARV和RMS的幅度增加。在肌肉运动到疲劳过程中表面肌电信号的时域值总体上呈上升趋势,这些时域值的变化通常与肌肉收缩力的大小有关,就同样的肌肉收缩状态下RMS能够较好的反应肌肉疲劳。
1.2 频域分析下的疲劳判别频域分析通过对sEMG自相关函数做快速傅里叶变换,根据功率谱密度(power spectrum density, PSD)电信号不同频段信号的分布情况,主要的特征参数有平均功率频率(mean power frequency, MPF)和中位频率(median frequency, MF)公式如下:
| $\begin{array}{l} {\rm{MPF}} = \frac{{\smallint _{_0}^{^\infty }f{\rm{PSD}}\left( f \right){\rm{d}}f}}{{\smallint _{_0}^{^\infty }{\rm{PSD}}\left( f \right){\rm{d}}f}}, \\ {\rm{MF}} = \frac{1}{2}\smallint _{_0}^{^\infty }{\rm{PSD}}\left( f \right){\rm{d}}f. \end{array} $ |
式中PSD(f)为表面肌电信号的功率谱密度函数。
疲劳时,功率谱大多由高频向低频漂移,MF和MPF也相应的下降[8]。Xiang等[9]研究两款自行车疲劳舒适度是采用MF的下降作为疲劳的判别标准。Yang等[10]研究人体颈部胸锁乳突肌的疲劳程度发现,MF和MPF首先呈现下降趋势。Higashi等[11]在研究肘关节弯曲等尺性收缩时表面肌电的MPF表现出下降的趋势。MF和MPF作为频谱移动的指标各有其优点:MF抗噪声干扰性强,适应的负荷水平范围较广,在各类肌肉及各种收缩中都随力的增加而增加;MPF较稳定,对于低负荷条件下的频谱变化有高度敏感性。
频域的双谱分析方法,它通过对第3顺序累积量的傅里叶变换,第3顺序累计量和双谱函数公式[12]如下:
| $ \begin{array}{l} c_{_3}^{^x}({\tau _1}, {\tau _2}) = E[x\left( k \right)x(k + {\tau _1})x(k + {\tau _2})], \\ B({f_1}, {f_2}) = \sum\limits_{{\tau _1} = - \infty }^\infty {\sum\limits_{{\tau _2} = - \infty }^\infty {c_{_3}^{^x}} } ({\tau _1} 、{\tau _2}){\rm{exp}}[-{\rm{j}}({\tau _1}{f_1} + {\tau _2}{f_2}))]. \end{array} $ |
式中:τ1、τ2分别为延迟;f1、f2分别为τ1、τ2在频域部分的对应。一个随机过程的非高斯性可以量化使用系数和估计[13]如下:
| $ {\rm{BC}}({f_1}, {f_2}) = \frac{{B({f_1}, {f_2})}}{{\sqrt {P({f_1})P({f_2})P({f_1} + {f_2})} }}. $ |
式中P(·)为功率谱。B(f1, f2)和BC(f1, f2)派生下来的双谱和(bispectrum sum, BS)、双相干和(bicoherence sum, BC)、双谱方差(bispectrum variance, BSV)和双方差(bicoherence variance, BCV)公式分别为:
| $ \begin{array}{l} {\rm{BS}} = \sum |B({f_1}, {f_2})|, \\ {\rm{BC}}\sum |{\rm{BC}}({f_1}, {f_2})|, \\ {\rm{BSV}} = E\{ {[B({f_1}, {f_2})-{\rm{mean}}(B({f_1}, {f_2}))]^2}, \\ {\rm{BCV}} = E\{ {[{\rm{BC}}({f_1}, {f_2})-{\rm{mean}}({\rm{BC}}({f_1}, {f_2}))]^2}\} . \end{array} $ |
Venugopal等[14]通过研究表明BS和BSV在实验者发生疲劳时区域出现独特的高值,BC和BCV不具有这类作用。相比于频域单谱中的MF和MPF,双谱分析能够在疲劳产生的区域产生独特的高值,能够更好地反应频域中疲劳变化的指标;但是双谱分析处理复杂,对于一些简单的系统,频域的单谱分析已经能够反应出肌肉的疲劳了。
2 时频指标下疲劳判别 2.1 短时傅里叶变换短时傅里叶变换(Short Time Fourier Transform, STFT)是最基本的时频分析方法[15]。它解决了FT不能表示频率分量时间局域化的问题。STFT变换的实质就是用一个可以移动的窗口函数对待测信号进行截取并分析。使用不同的窗口函数得的结果不同,同时窗口宽度的设置也对结果有一定的影响,窗口宽度过低会使频率分辨率降低,而过高的窗口宽度则会影响平稳性假设。
陈飚等[16]探讨STFT和FFT(快速傅里叶变换)在肌肉疲劳中肌电信号的中位频率的差异,研究结果显示这两种变换后的MF的斜率无明显差异均可用来表示产生了肌肉疲劳,疲劳检出率为60%,检出率STFT大于FFT见表 1。Bai等[17]用STFT在肘关节恒力收缩和动态收缩条件检测肌肉的疲劳,结果表明在疲劳产生的过程中MF呈现出下降趋势。Alzaman等[18]研究动态收缩下的肌肉,使用STFT变换后发现肌肉疲劳时MF和MNF表现出下降趋势。
| 表 1 FFT和STFT检出率比较 Table 1 FFT and STFT detection rate comparison |
小波变换(wavelet transform, WT)也是一种将信号在频段分解的积分变换,与短时傅里叶变换的区别在于划分频带宽度时所使用的方式不一样[19]。通过对时间尺度的变化可以对信号局部的细节起到放大和缩小的作用,小波分析具备实现信号多分辨率变换的特性[20]。
小波变换的核心在于基准波函数的选择,常用的小波有Marr小波、Morlet小波等,不同的小波的基准函数具有不用的特征。颜芳等[21]研究电刺激诱发表面肌电,用CWT分析单个M-波,肌肉疲劳发生时,CWT(使用Mexihat和-Mexihat小波)的尺度因子呈增长趋势。Chowdhury等[22]使用Daubechies45小波用于研究的步态时肌肉的疲劳,结果表明肌电图的功率谱向低频移动。
2.3 Cohen类时频分布Cohen类时频分布是一系列以Winger-Ville为原型的变形,实质是将信号的能量分布于时频平面内,避免线性时频表达中时间分辨率和频率分辨率的相互牵制。
Wingner-Ville分布(WVD)是一种常用的双线性时频分布,是Cohen类时频分布最常见的类型,是分析单分量事变信号的重要工具。WVD可以看做是信号能量在时域和频域中的分布函数,即能量在WVD在时间和频率上的双重积分,WVD在时域和频域均可获得很高的分辨率并且具有一些很好的特性,包括时移不变性、频移不变性、时域或频域压扩特性及边缘特性等。
Knaflitz等[23]检测实验者在骑车过程中腿步肌肉的表面肌电信号,发现在疲劳产生的过程中Choi-Williams分布中的瞬时平均频率(instantaneous mean frequency, IMNF)值比初始值低5%。牟永阁等[24]分析肌肉动态收缩期间的表面肌电信号的Choi-Williams分布(CWD),随着疲劳的产生频率成分向低端压缩。
3 非线性方法指标下疲劳判别 3.1 AR模型自回归(autoregressive,AR)参数模型法是一种从最小均方误差拟合角度对随机信号进行分析的方法[25]。该方法在截取数据时,不受窗口函数的影响,因此对短数据序列能给出更为精确的估计。实际上,当信号长度不能再增加时,不同的算法可以给出不同的分辨率,现代谱估计方法一般要优于经典谱估计方法,因为其中的算法对信号长度的扩展,从而提高了分辨率。
Paiss等[26]和Merletti等[27-28]研究表面肌电的AR模型,通过对第一AR系数和第1个反射系数和模型误差的归一化能量,在局部疲劳期间随时间下降。
3.2 熵方法近视熵(ApEn)是用一个非负数来表示时间序列的复杂性,时间序列越复杂对应的近视熵越大[29]。近视熵的主要特点是使用较少的数据量来估算出一个相对稳定的统计值。拥有较好的抗干扰能力;并且适用于随机信号,因此特别适用于肌电信号这样的生理性时间序列的分析。
模糊近视熵(fApEn)是在近似熵方法的基础上改进来的,它是利用模糊隶属度函数来定义向量的相似性。在fApEn中,采用模糊隶属函数,作为在模糊隶属函数基础上一个新的相似指数的结果,点越接近就变得越相似[30]。辛几何(SG)是一种相空间的几何学,是针对哈密顿体系提出的,而一切守恒真实物理过程都可以表示为哈密顿体系[31]。
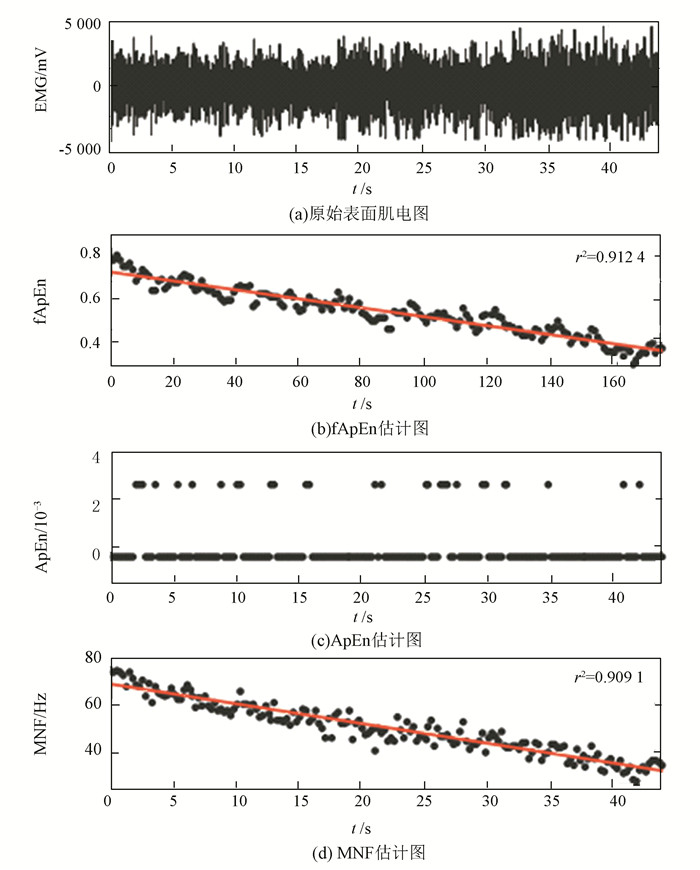
汪晨等[32]在研究腕关节60%MVC直至竭力的情况下,采集表面肌电信号分析,肌肉疲劳初期和肌肉疲劳末期fApEn下降,且变化率达到了84.38%见表 2,说明fApEn能够有效地判断肌肉疲劳,同时文献[32]等也发现了使用辛几何熵来判断疲劳时,在疲劳期,辛几何熵有下降的趋势,但是没有fApEn的幅度大,fApEn能够很好地反应出疲劳变化的过程。Xie等[33]研究局部肌肉疲劳的过程中发现在肌肉的疲劳期,fApEn显著下降,如图 1所示,图 1(b)为fApEn,图 1(c)为ApEn,图 1(d)为频域指标中的MNF。从图 1中可以看出fApEn呈下降趋势,与频域中的判别是一致的,而ApEn值没有变化。
| 表 2 模糊近似熵(fApEn)和辛几何熵(SGEn)对应的熵值变化率 Table 2 The entropy change rate of fuzzy approximate entropy (fApEn) and symplectic geometric entropy (SGEn) |
|
图 1 ApEn和fApEn方法比较 Figure 1 ApEn and fApEn method comparison chart |
蒋明峰等[34]使用小波分析与神经网络相结合的方法实现对正常和疲劳肌电信号的识别。采用Daubechies4小波作为基函数对原始肌电信号进行小波分解,采用不同的尺度函数提取与疲劳肌电相关的特征信号。结果显示使用人工神经网络对正常肌电信号和疲劳肌电信号的分类过程中,结合小波分析的方法,可以有效地提高对肌电信号识别准确率,原始肌电信号直接分类的准确率为55%,使用了小波分解后的准确率高达87.5%。
王乐军等[35]也使用小波包分析与人工神经网络相结合的方法研究肌肉疲劳过程中表面肌电信号的变化。按等时间间隔将sEMG将信号划分为不同的段,然后比较不同分解层数下各频段的能量并归一化处理,并以此作为输入,以运动过程中归一化后的输出功率作为输出,构造人工神经网络模型。结果显示,随着运动时间的增加和疲劳程度的加深,表面肌电信号经小波分解后低频段能量增加,高频段能量衰减,但能量的增加与衰减集中在比较大的频段范围内,人工神经网络能够提高良好的精度,预测值的准确率高达99%。
荣瑶等[36]对表面肌电信号进行小波包变换得到第3层和第4层节点的分解系数,由此计算出各个节点响应频段能量并在归一化处理后作为特征向量,然后将特征向量通过BP神经网络分类器来完成识别,识别率最高可达到66.07%。
综上所述可得出, 文献[35]使用的将各频段能量归一化后处理的方法准确率高达99.0%, 能够非常有效地识别疲劳。
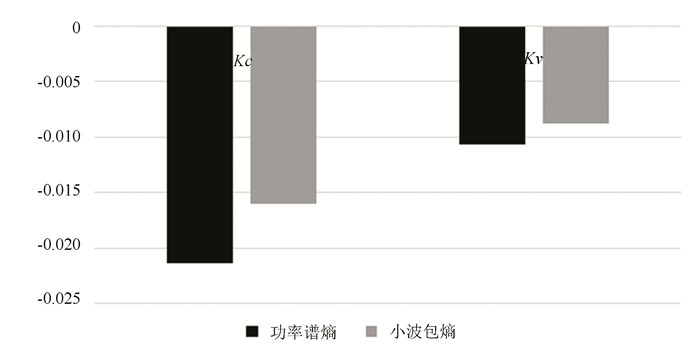
3.3.2 功率谱熵和小波包熵陈伟婷等[37]将频率分析和非线性动力学方法结合起来。利用表面肌电信号在不同频率分布不均匀的特点将信号能量分解到不同频带,据此计算功率谱/小波包与熵相结合的功率谱熵/小波包熵来衡量系统的复杂度,进而衡量肌肉的疲劳程度。实验显示,随着肌肉逐渐疲劳,功率谱熵和小波包熵呈下降趋势如图 2(其中:e为非振动力量训练,v为振动力量训练)功率谱熵和小波包熵拟合曲线斜率变化所示,随着疲劳程度的增加,非振动肌电和振动肌电的功率谱熵和小波包熵均下降功率谱熵的下降率更高,熵可以用来评价肌肉疲劳的程度,下降的速率也可以反映达到疲劳状态的速度。
|
图 2 功率谱熵和小波包熵拟合曲线斜率变化 Figure 2 The slope of the fitting curve for power spectral entropy and wavelet packet entropy |
从上个世纪50年代后使用sEMG来分析研究肌肉的疲劳问题以来,在时域和频域领域早已一致的认为肌肉疲劳过程中伴随着频谱的左移和时域指标上的幅值增加。在时频领域的短时傅里叶(STFT)、Cohen时频主要的Choi-Williams分布(WVD)相继出现后,发现小波变换(WT)能够使用不同的窗口函数,克服STFT频率分辨率的限制,能够更好地判别肌肉的疲劳; 同时相比WVD,用WT方法得出的MF则更为平滑。用非线性动力学方法研究肌肉疲劳过程中肌-电的关系,一直是近几年研究的最新趋势,通过对信号熵和AR模型的研究,也获得了在肌肉疲劳的过程中,肌电信号的熵减小的趋势; 使用AR模型通过对第一AR系数和第1个反射系数和模型误差的归一化能量,在局部疲劳期间随时间下降。上述关于肌肉疲劳期间表面肌电信号的特征表明,这些参数能够反映肌肉活动的生理特征。基于目前的研究现状,线性指标变化的可靠性方面,基本已经达成共识;非线性混沌动力学原理在肌电疲劳分析尚且处于初期阶段,非常适合于在表面肌电、心电、脑电等生物医学信号以及其他一些带有噪声且数据长度较短的信号分析,有着广阔的应用前景。
| [1] |
TAELMAN J, VANDERHAEGEN J, ROBIJNS M, et al. Estimation of muscle fatigue using surface electromyography and near-infrared spectroscopy[J]. Advances in Experimental Medicine and Biology, 2011, 701(1): 353–359.
DOI:10.1007/978-1-4419-7756-4_48( 0) 0)
|
| [2] |
ZAMAN A A, AHAD M A, FERDJALLAH M, et al. A new approach for muscle fatigue analysis in young adults at different MVC levels[C]//Proceedings of the 48th Midwest Symposium on Circuits and Systems. Covington, KY:IEEE, 2005.DOI:10.1109/MWSCAS.2005.1594347.
( 0) 0)
|
| [3] |
张佑琏, 马国际. 运动性肌肉疲劳的表面肌电信号特征研究[J]. 湖北体育科技, 2011, 30(1): 42–44.
ZHANG Youlian, MA Guoji. Muscle fatigue characteristics of the surface EMG[J]. Hubei Sports Science, 2011, 30(1): 42–44. DOI:10.3969/j.issn.1003-983X.2011.01.018(  0) 0)
|
| [4] |
黄鹏. 便携式肌肉疲劳分析系统研制[D]. 合肥: 中国科学技术大学, 2015.
HUANG Peng. Development of a portable muscle fatigue analysis system[D]. Hefei: University of Science and Technology of China, 2015.
( 0) 0)
|
| [5] |
INBAR G F, PAISS O, ALLIN J, et al. Monitoring surface EMG spectral changes by the zero crossing rate[J]. Medical and Biological Engineering and Computing, 1986, 24(1): 10–18.
DOI:10.1007/BF02441600( 0) 0)
|
| [6] |
VIITASALO J H T, KOMI P V. Signal characteristics of EMG during fatigue[J]. European Journal of Applied Physiology and Occupational Physiology, 1977, 37(2): 111–121.
DOI:10.1007/BF00421697( 0) 0)
|
| [7] |
MADELEINE P, FARINA D, MERLETTI R, et al. Upper trapezius muscle mechanomyographic and electromyographic activity in humans during low force fatiguing and non-fatiguing contractions[J]. European Journal of Applied Physiology, 2002, 87(4): 327–336.
DOI:10.1007/s00421-002-0655-8( 0) 0)
|
| [8] |
MING Dong, WANG Xin, XU Rui, et al. sEMG feature analysis on forearm muscle fatigue during isometric contractions[J]. Transactions of Tianjin University, 2014, 20(2): 139–143.
DOI:10.1007/s12209-014-2181-2( 0) 0)
|
| [9] |
XIANG Zhongxia, LI Ya'nan, TIAN Guan, et al. Analysis and comparison of safety and fatigue comfort of postal bicycles based on finite element method and sEMG[J]. Tran-sactions of Tianjin University.August, 2013, 19(4): 272–278.
DOI:10.1007/s12209-013-1975-y( 0) 0)
|
| [10] |
YANG Lifang, KANG Bo. Study on Human neck muscles' comfort of different height levels based on sEMG method[C]//Proceedings of the 6th International Asia Conference on Industrial Engineering and Management Innovation.Paris:Atlantis press, 2015: 563-574. DOI:10.2991/978-94-6239-148-2_55.
( 0) 0)
|
| [11] |
HIGASHI T, TSURUSAKI T, FUNASE K, et al. Effect of the elbow joint posture on elbow flexor fatigability and muscle strength during isometric contraction[J]. Rigakuryoho Kagaku, 2004, 19(2): 121–125.
DOI:10.1589/Rika.19.121( 0) 0)
|
| [12] |
OROSCO E C, LOPEZ N M, DI SCIASCIO F. Bispectrum-based, features classification for myoelectric control[J]. Biomedical Signal Processing and Control, 2013, 8(2): 153–168.
DOI:10.1016/j.bspc.2012.08.008( 0) 0)
|
| [13] |
SIGL J C, CHAMOUN N G. An introduction to bispectral analysis for the electroelcephalogram[J]. J Clin Monitor, 1994, 10(6): 392–404.
DOI:10.1007/BF01618421( 0) 0)
|
| [14] |
VENUGOPAl G, RAMAKRISHNAN S. Analysis of progressive changes associated with muscle fatigue in dynamic contraction of biceps brachii muscle using surface EMG signals and bispectrum features[J]. Biomedical Engineering Letters, 2014, 4(3): 269–276.
DOI:10.1007/s13534-014-0135-1( 0) 0)
|
| [15] |
王奎. sEMG常用时频方法及其用于分析动态肌肉疲劳时的策略[J]. 中国运动医学杂志, 2010, 29(1): 104–108.
WANG Kui. sEMG time frequency method and its application in dynamic muscle fatigue analysis[J]. Chinese Journal of Sports Medicine, 2010, 29(1): 104–108. DOI:10.16038/j.1000-6710.2010.01.029(  0) 0)
|
| [16] |
陈飚, 王正伦, 赵磊, 等. 短时和快速傅里叶变换用于动态活动下表面肌电频谱分析的比较研究[J]. 工业卫生与职业病, 2012, 38(3): 144–150.
CHEN Biao, WANG Zhenglun, ZHAO Lei, et al. A comparative study on the short time-and fast-Fourier based spectral analysis of EMG signals in dynamic exercises[J]. Industry Health & Occupation Disease, 2012, 38(3): 144–150. DOI:10.13692/j.cnki.gywsyzyb.2012.03.002(  0) 0)
|
| [17] |
BAI Fengjun, LUBECKI T M, CHEW C M, et al. Novel time-frequency approach for muscle fatigue detection based on Semg[C]//Proceedings of the Biomedical Circuits and Systems Conference.Hsinchu, Taiwan:IEEE, 2012:364-367.DOI: 10.1109/BioCAS.2012.6418421.
( 0) 0)
|
| [18] |
ALZAMAN A, FERDJALLAH M, KHAMAYSEH A. Muscle fatigue analysis for healthy adults using TVAR model with instantaneous frequency estimation[C]//Proceedings of the 38th Southeastern Symposium on System Theory.Cookeville, TN:IEEE, 2006: 44-47. DOI: 10.1109/SSST.2006.1619081
( 0) 0)
|
| [19] |
王东岩, 李庆玲, 杜志江, 等. 小波分析在表面肌电信号(sEMG)研究中的应用[J]. 黑龙江大学自然科学学报, 2008, 25(4): 431–436.
WANG Dongyan, LI Qingling, DU Zhijiang, et al. Wavelet transform and its application in Semg analysis[J]. Journal of National Science of Heilongjiang University, 2008, 25(4): 431–436. DOI:10.3969/j.issn.1001-7011.2008.04.003(  0) 0)
|
| [20] |
蔡立羽, 王志中, 张海虹. 小波变换在表面肌电信号分类中的应用[J]. 生物医学工程学杂志, 2000, 17(3): 281–284.
CAI Liyu, WANG Zhizhong, ZHANG Haihong. Surface EMG singal claassification using wavelet transform[J]. Journal of Biomedical Engineering, 2000, 17(3): 281–284. DOI:10.3321/j.issn:1001-5515.2000.03.009(  0) 0)
|
| [21] |
颜芳, 曾孝平, 何庆华, 等. 肌肉疲劳过程中电诱发表面肌电信号的小波分析[J]. 重庆大学学报:自然科学版, 2005, 28(1): 77–81.
YAN Fang, ZENG Xiaoping, HE Qinghua, et al. Wavelet analysis of electrically evoked surface electromyogrphy signals during muscle fatigue[J]. Journal of Chongqing University(National Science Edition), 2005, 28(1): 77–81. DOI:10.3969/j.issn.1000-582X.2005.01.019(  0) 0)
|
| [22] |
CHOWDHURY REAZ BMI, ISIAMMT. Wavelet transform to recognize muscle fatigue[C]//Proceedings of the Third Asian Himalayas International Conference on Internet.Kathmandu, Nepal:IEEE, 2012: 1-5. DOI: 10.1109/AHICI.2012.6408445.
( 0) 0)
|
| [23] |
KNAFLITZ M, MOLINARI F, ELETTRONICA D. Assessment of muscle fatigue during biking[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2003, 11(1): 17–23.
DOI:10.1109/TNSRE.2003.810425( 0) 0)
|
| [24] |
牟永阁, 彭承琳, 郑小林, 等. 肌肉动态收缩期间表面肌电信号的时频分析[J]. 生物物理学报, 2004, 20(4): 323–328.
MOU Yongge, PENG Chenglin, ZHENG Xiaolin, et al. Time-frequency analysis of surface myoelectric signals during dynamic contractions[J]. Acta Biophysica Sinica, 2004, 20(4): 323–328. DOI:10.3321/j.issn:1000-6737.2004.04.011(  0) 0)
|
| [25] |
皮喜田, 陈峰, 彭承琳. 利用表面肌电信号评价肌肉疲劳的方法[J]. 生物医学工程学杂志, 2006, 23(1): 225–229.
PI Xitian, CHEN Feng, PENG Chenglin. Methods applied to muscle fatigue assessment using suface myoelectric siganals[J]. Journal of Biomedical Engineering, 2006, 23(1): 225–229. DOI:10.3321/j.issn:1001-5515.2006.01.051(  0) 0)
|
| [26] |
PAISS O, INBAR G F. Autoregressive modeling of surface EMG and its spectrum with application to fatigue[J]. IEEE Transactions on Biomedical Engineering, 1987, BME-34(10): 761–770.
DOI:10.1109/TBME.1987.325918( 0) 0)
|
| [27] |
MERLETTI R, GULISASHVILI A, LO CONTE L R. Estimation of shape characteristics of surface muscle signal spectra from time domain data[J]. IEEE Transactions on Biomedical Engineering, 1995, 42(8): 769–776.
DOI:10.1109/10.398637( 0) 0)
|
| [28] |
LO CONTE L R, MERLETTI R. Advances in processing of surface myoelectric signals: part 2[J]. Medical and Biological Engineering and Computing, 1995, 33(3): 362–384.
DOI:10.1007/BF02510519( 0) 0)
|
| [29] |
陈伟婷, 王志忠, 李晓浦. 振动刺激对肌肉疲劳进程的影响[J]. 北京生物医学工程, 2007, 26(1): 60–64.
CHEN Weiting, WANG Zhizhong, LI Xiaopu. Effect of vibration stimulation on muscle fatigue[J]. Beijing Biomedical Engineering, 2007, 26(1): 60–64. DOI:10.3969/j.issn.1002-3208.2007.01.015(  0) 0)
|
| [30] |
ROERDINK M, HLAVACKOVA P, VUILLERME N. Effects of plantar-flexor muscle fatigue on the magnitude and regularity of center-of-pressure fluctuations[J]. Experimental Brain Research, 2011, 212(3): 471–476.
DOI:10.1007/s00221-011-2753-5( 0) 0)
|
| [31] |
牛迅, 曲峰, 王宁. 基于EMD和辛几何的运动员表面肌电信号分析与评价[J]. 中国海洋大学学报, 2005, 35(1): 125–129.
NIU Xun, QU Feng, WANG Ning. Evaluating sprinters' surface EMG signals based on EMD and symplectic geometry[J]. Periodical of Ocean University of China, 2005, 35(1): 125–129. DOI:10.3969/j.issn.1672-5174.2005.01.025(  0) 0)
|
| [32] |
汪晨, 和卫星, 陈晓平. 基于模糊近视熵与辛几何的肌肉疲劳分析[J]. 现代仪器与医疗, 2013, 19(4): 1–4.
WANG Chen, HE Weixing, CHEN Xiaoping. Analysis of fatigue muscle based on fuzzy approximate entropy and symplectic genmetry[J]. Modern Instruments, 2013, 19(4): 1–4. (  0) 0)
|
| [33] |
XIE Hongbo, GUO Jingyi, ZHENG Yongping. Fuzzy approximate entropy analysis of chaotic and natural complex systems: detecting muscle fatigue using electromyography signals[J]. Annals of Biomedical Engineering, 2010, 38(4): 1483–1496.
DOI:10.1007/s10439-010-9933-5( 0) 0)
|
| [34] |
蒋明峰, 王洪. 基于小波分析与神经网络相结合的表面肌电信号识别的研究[J]. 生物医学工程研究, 2005, 24(1): 50–52.
JIANG Mingfeng, WANG Hong. The classification of surface emg signal based on wavelet transform and neural networks[J]. Journal of Biomedical Engineering Research, 2005, 24(1): 50–52. DOI:10.3969/j.issn.1672-6278.2005.01.015(  0) 0)
|
| [35] |
王乐军, 黄勇, 龚铭新, 等. 小波包分析与人工神经网络相结合探索运动性肌肉疲劳过程中sEMG变化特征[J]. 体育科学, 2009, 29(12): 51–55.
WANG Lejun, HUNAG Yong, Gong Mingxin, et al. Study on characteristics of sEMG change during the process of muscle fatigue using wavelet packet transformation and artificial neural network[J]. China Sport Science, 2009, 29(12): 51–55. DOI:10.3969/j.issn.1000-677X.2009.12.007(  0) 0)
|
| [36] |
荣瑶, 郝冬梅, 张琰, 等. 基于小波包能量分析的肌肉疲劳识别方法[J]. 北京生物医学工程, 2012, 31(6): 579–585.
RONG Yao, HAO Dongmei, ZHANG Yan, et al. Recognition of muscle fatigue using wavelet packet energy transform[J]. Beijing Biomedical Engineering, 2012, 31(6): 579–585. DOI:10.3969/j.issn.1002-3208.2012.06.07(  0) 0)
|
| [37] |
陈伟婷, 王志中, 胡晓, 等. 基于熵的动态收缩sEMG信号疲劳特征分析[J]. 中国医学物理杂志, 2006, 23(3): 204–208.
CHEN Weiting, WANG Zhizhong, HU Xiao, et al. Entropy analysis of semg signal during dynamic contractions for assessing muscle fatigue[J]. Chinese Journal of Medical Physics, 2006, 23(3): 204–208. DOI:10.3969/j.issn.1005-202X.2006.03.013(  0) 0)
|
 2017, Vol. 15
2017, Vol. 15


