The biological function of protein will decide how to design drug with specific therapeutic property, and to finally grow biological polymers with the specific material properties in a synthetic way. We know that protein's biological function heavily depends on its spatial structure. So protein structure prediction is one of the fundamental tasks in bioinformatics study[1]. There exist a variety of models attempting to simplify the problem by abstracting only the "essential physical properties" of real proteins[2]. The abstracted models can be categorized into three different classes: full atom model[3], AB non-lattice model[4] and hydrophobic-hydrophilic (HP) lattice model[5]. For HP model, the three-dimensional space was often represented by a lattice, and residues which are adjacent in the chain must be placed at adjacent points in the lattice.
HP model was proposed by Dill and his collaborators in 1995[5]. Now chemists evaluate new hypothesis of protein structure by HP model. And the efficiency of a new folding algorithm will be confirmed by this model[6]. Based on Anfinson's hypothesis, the energy of natural conformation is assumed to be minimal. For the stable structure of protein, hydrophobic amino acids form a core and hydrophilic amino acids shield the core from surrounding solvents.
Traditionally, 2D HP model was studied on square lattice[7-9], because it has many associated benchmarks, large amount of data accumulated over years and the availability of comparison with different strategies and modeling methods. Moreover from the view point of realistic meaning of HP model, it is not natural to limit the native state to be a square lattice or a rectangle lattice. Therefore we will force to extend the model and find more native configuration of protein on rhombus lattice in this paper, and more flexible and different structures can be expected. Little work about predicting protein structure on rhombus lattice was showed now.
However, HP model was hard to solve in computation and has been proved that is NP-hard problem by Cresenzi[10] et al. So heuristic search algorithms for a variety of lattice models have been proposed and proven usefully to explore the prediction of protein structure. How to find an effective heuristic method will be a primary research objective for 2D HP lattice model. In past years, some heuristic search algorithm has been developed[11-13]. Particle swarm optimization (PSO) algorithm[14] is a type of heuristic algorithm. It was successfully used to predict protein structure on square lattice[15]. We will modify PSO algorithm to fold the amino acid sequence on rhombus lattice.
This paper was organized as follows. Section 2 established the 2D HP mathematical model. The extended PSO algorithm was described in section 3. Numerical simulations would be showed in section 4. Section 5 concluded the paper with discussion.
2 HP modelHP model is assumed that low energy conformations are compact with a hydrophobic core, since the hydrophobic residues have to be buried inside to yield a low energy structure, while the hydrophilic residues are forced to the surface. In the HP model, three facts are abstracted: from the geometrical point view, protein structure is simplified as bond structure which only includes C atoms; then twenty kinds of amino acids are classified as hydrophobic (H) and polar (P); at last, the interactions between non-covalently hydrophobic neighbors play the dominant role in the encoding of proteins. So the conformation of amino acid sequence is an embedding the sequence into the lattice such that adjacent amino acids occupy adjacent grid points in the lattice and no grid point is occupied by more than one. The H-H bond, H-P bond and P-P bond are formed and energies are evaluated EHH = -1, EHP = 0 and EPP = 0. Because the stable structure is with lowest free energy, an ideal structure of a protein is to maximize the number of HH bonds.
We knew that 2D HP model was a matter of matching amino acids to lattice points such that the most H-H bonds can be found. In this paper, we forced on rhombus lattice, in which every lattice point has six neighbor points, since diagonal can be used to compute HH bond. Based on the biological conditions and the character of rhombus lattice, we established mathematical model for 2D HP model on rhombus lattice as follows.
| $ \begin{array}{l} \max \;f\left( X \right) = \frac{1}{2}{s^{\rm{T}}}XC\\ s.t\;X{e^0} = {e^1}, \\ \;\;\;\;\;{X^{\rm{T}}}{e^1} = d, \\ \;\;\;\;\;{x_{ij}} = {x_{\left( {i + 1} \right)k}} = 1, \exists k \in N\left( j \right), i = 1, 2, ..., n. \end{array} $ |
Here, X=(xij) is n×m matrix, if the ith amino acid occupies the vertex j of rhombus lattice, then xij=1, else xij=0, and X are optimization variables. For example, three amino acids occupied five lattice points, then
| $ \mathit{\boldsymbol{X = }}\left( {\begin{array}{*{20}{c}} 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 \end{array}} \right). $ |
It means that the first amino acid visited the second lattice point, the second amino acid visited the fifth lattice point, and the third amino acid visited the forth lattice point.
s∈Rn is a column vector, in which element si=1 if ith amino acid is hydrophobic, else si=0. By this way, we translated letter sequence to 01 sequence. For example, the amino acid sequence is HHPPHPHPP, then s=(1, 1, 0, 0, 1, 0, 1, 0, 0)T.
Let N(j) be the set of all adjacent vertexes of the jth vertex. Here, adjacent vertex is with shortest distance to jth vertex. |N(j)| denotes the number of elements in the set N(j). ej∈R|N(j)| is a column vector that all elements are 1. Before simulating, we will manage the vertexes in number order. Generally, we started to order from the left vertex of bottom row as follows:
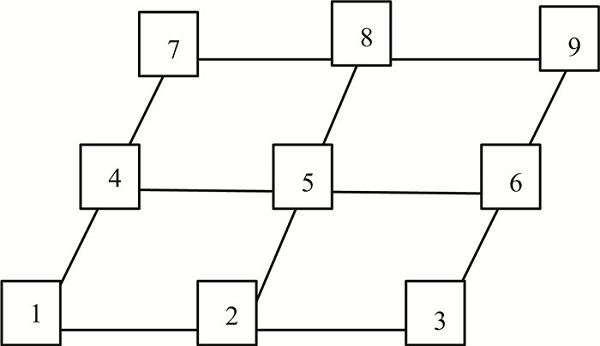
|
In this figure, N(5)={2, 3, 4, 6, 7, 8}, N(1)={2, 4}, so N(5)=6, N(1)=2, and e5=(1, 1, 1, 1, 1, 1)Τ∈R6, e1=(1, 1)Τ∈R2.
C=(c1, c2, …, cm)Τ∈Rm, cj=sΤXBjej. Bj denotes a n×|N(j)| matrix, the number of subscript seat for N(j)k is 1 in the kth column, others is 0. For example, if N(j)={y2, y5}, then
| $ \mathit{\boldsymbol{B}}_j^{\rm{T}} = \left( {\begin{array}{*{20}{c}} 0 & 1 & 0 & 0 & 0 & 0 & \cdots & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & \cdots & 0 \end{array}} \right). $ |
So objective function f(X) presents the number of HH bonds when amino acid sequence was folded on rhombus lattice.
The constraint conditions were satisfied with biologicalcharacters, in which:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;{e^0} = {\left( {1, 1, \cdots, 1} \right)^{\rm{T}}} \in {R^m}, \\ {e^1} = {\left( {1, 1, \cdots, 1} \right)^{\rm{T}}} \in {R^n}, d \in {R^m}, {d_j} = 0/1. \end{array} $ |
The first constraint condition means that one amino acid can just only occupy one vertex; The second constraint condition means that every vertex can be used once at most; The third constraint condition means that adjacent amino acids in chain must occupy adjacent vertexes on lattice.
In this way, we translated the protein structure prediction problem to a mathematical optimization problem.
3 Optimization methodBased on the problem (1), we knew that it was NP-hard[10], so heuristic algorithms need be considered. Particle swarm optimization (PSO) method is a kind of heuristic method. It is adapt at solving the matching problem. PSO algorithm was presented by Kennedy and Eberhart in 1995, inspired by the social behaviors of bird flocking[14]. This method only requires that the problem is computable with less parameters adjusted. In addition, the principle of this method is that it can be easily implemented and applied in practice. Currently, PSO algorithm has been successfully used to solve protein structure prediction problem on the 2D square lattice[7].
Hence, we believed that it is feasible to predict protein structure on rhombus lattice by PSO. But because of the difference of square lattice and rhombus lattice, PSO algorithm should be modified to avoid the multi-mapping problem and local optimal problem. The flowchart of modified PSO algorithm was demonstrated in Table 1 for protein structure folding problem on rhombus lattice.
| Table 1 Flowchart of modified PSO for folding protein structure on rhombus lattice |
There are two possible choices for n amino acids and m lattice points. If n=m, the conformation of protein is regarded as compact for HP lattice model; else m>n, the conformation is non-compact. To assess its performance, we apply the hybrid of particle swarm optimization method and optimal strategies to some standard benchmark instances with different length (shown in Table 2) for 2D HP model on rhombus lattice. These instances were used by PSO method[11] and elastic net algorithm[15] on square lattice. We know there are six neighbors of lattice point on rhombus lattice, but four neighbors on square lattice. So there are more HH bonds on rhombus lattice than on square lattice. The structure will be more flexible and native.
| Table 2 Four standard benchmark instances for simulation |
In the following figures, polar amino acid will be depicted as hollow square. Hydrophobic amino acid is depicted as solid circle. The black lines show the covalent bond between the adjacent amino acids.
4.1 Sequence 1This sequence contains 17 amino acids. Because 17 is not the product of two integers, we can just only obtain the non-compact conformations on rhombus lattice, and folding on square lattice is not possible either. It was embedded into a 5×5 rhombus lattice of R2 with ten HH bonds by our method. One of the non-compact conformations was demonstrated in Fig. 1(b). The optimal conformation with eight HH bonds was found in Ref.[7] on square lattice in Fig. 1(a). The configurations on rhombus lattice are more flexible and stable than ones on square lattice, because of more HH bonds. It means that our mathematical model and method can be applied to fold this type of amino acid sequences.
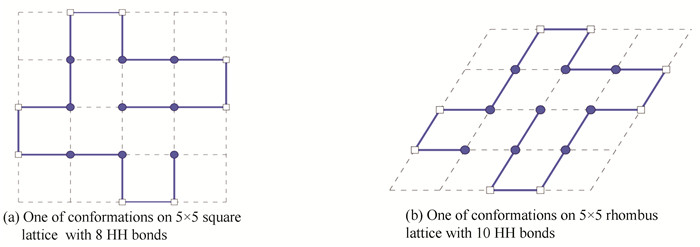
|
Figure 1 Un-compact conformations of length 17 amino acid sequence |
This sequence with 20 amino acids was embedded into 5×5 square lattice and 5×5 rhombus lattice respectively by our model and method. The non-compact conformation on rhombus lattice was shown in Fig. 2(a) with 12 HH bonds. To compare, we can find the optimal non-compact conformations with 9 HH pairs on square lattice. The result was demonstrated in Fig. 2(b).
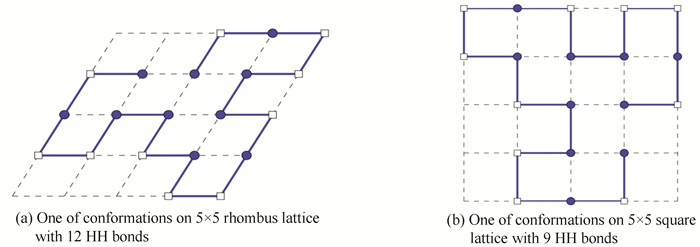
|
Figure 2 Un-compact conformations of length 20 amino acid sequence |
It indicated that our new method can not only obtain the non-compact conformations on rhombus lattice, but also on square lattice. Comparing Fig. 2(a) and Fig. 2(b), we knew that the optimal structure was more flexible on rhombus lattice. Firstly, this is naturally since rhombus allows the diagonal interaction. Secondly, the rhombus lattice can obtain tighter core with 12 HH bonds than square lattice. But we can find that Fig. 2(a) and Fig. 2(b) are the same spatial structures.
4.3 Sequence 3The length of this sequence is 25. It was embedded into a 5×5 rhombus lattice and a 5×6 rhombus lattice respectively. We can find the optimal compact conformation with 12 HH bonds on the rhombus lattice and optimal non-compact conformations with 12 HH bonds. One of compact conformations was shown in Fig. 3(a), and one of non-compact conformations was demonstrated in Fig. 3(b).
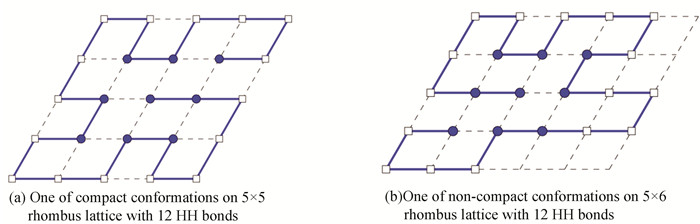
|
Figure 3 Compact and un-compact conformations of length 25 amino acid sequence |
It indicated that our new method can not only compute compact conformations, but also non-compact conformations on rhombus lattice. It means that our model and method can be applied to fold compact conformation and non-compact conformation for any sequence. Despite of conformations with the same HH bonds, we knew that the non-compact structure is more flexible and nature than compact ones. It is satisfied with biological characters of protein.
4.4 Sequence 4This sequence was computed by Ref.[15] on square lattice and obtained the compact conformations with 20 HH bonds. By our model and method, it was simulated on 6×6 lattice. The compact conformations can be found also on rhombus lattice. 33 HH pairs were obtained for the minimal free energy of this sequence on rhombus lattice. The compact figures of sequence 4 on square lattice and on rhombus lattice were shown in Fig. 4(a) and Fig. 4(b), respectively.
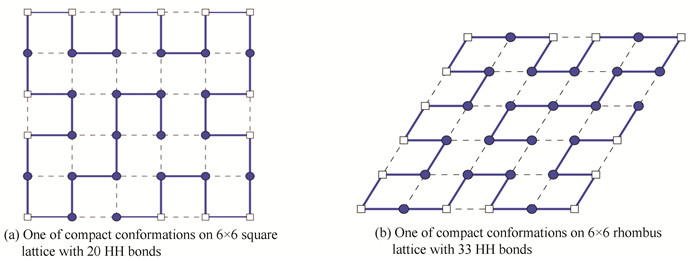
|
Figure 4 Compact conformations of length 36 amino acid sequence |
The results of this sequence showed that structure is more stable with minimal free energy. Since it is more difficult for obtaining compact conformation than non-compact conformation, our model and method are feasible and effective for folding conformation on rhombus lattice with more HH bonds. In addition, the conformations on rhombus lattice are more flexible and native than on square lattice.
4.5 Comparing the computing timeBased on the above sequences, we compared the computing time of all sequences. It was shown in Table 3.
| Table 3 Computing time of sequences in table |
In the table, CT is computing time of amino acid sequence on rhombus. We knew that the computing time will be more with longer chain. Computing time of non-compact conformation was longer than one of compact conformation, since more vertexes were matched with amino acids. It was regretful that Refs.[11, 15] do not have computing time of conformation on square lattice for these sequence, we do not compare computing time between two kinds of lattice.
4.6 Comparing with real protein structuresIt is necessary to compare the configurations obtained by extended PSO with real protein structures. For performing such task, the procedure will be shown as follows.
Step1 Obtaining the configurations on rhombus lattice by PSO through HP model.
Step2 Reconstructing the all-atom structure of the configurations.
Step3 Finding the real structures of the same amino acid sequences from Protein Data Bank.
Step4 Aligning between the real structures and obtained all-atom structures.
Step5 Calculating the root mean square error to express the degree of spatial similarity among the _ carbons.
5 ConclusionPredicting protein structure from the amino acid sequence on rhombus lattice was studied in this paper. We proposed a mathematical model, in which the optimal variable is a n×m matrix. In the matrix just only n variables is 1, others is 0 and in every column and in every row just only one variable is 1.
For this model, it is easy to perform simulation. The results indicated that the hybrid of extended PSO algorithm can find conformations with minimal free energy. The compact and non-compact conformations can be obtained. And it can fold the sequence with arbitrary length. The results indicated that our model and method are effective.
There are many future directions to pursuit. Firstly, because HP model just only considered the interaction of hydrophobic and hydrophobic for folding low energy conformation, conformations of amino acid sequence by HP model is an unnatural structures. In the future, for obtaining more native structures modified model need be considered. Secondly, we know that structure of protein is three dimensional, so hybrid of modified PSO need be applied to simulate on 3D lattice. Thirdly, it is necessary to achieve comparision between simulated results and real protein structures. In a word, we believe that our model and method offers considerable potential for protein structure prediction problem.
| [1] |
ABU S M, MOHAMMAD S R. On the protein folding problem in 2D-triangular lattices[J]. Algorithms for Molecular Biology, 2013, 8(1): 30.
DOI:10.1186/1748-7188-8-30( 0) 0)
|
| [2] |
SHAW D L, ISLAM A S, RAHMAN M S, et al. Protein folding in HP model on hexagonal lattices with diagonals[J]. BMC Bioinformatics, 2014, 15(Suppl 2): S7.
DOI:10.1186/1471-2015-15-S2-S7( 0) 0)
|
| [3] |
KIM S Y, KWAK W. All-atom simulation study of protein PTH(1-34) by using the Wang-Landau sampling method[J]. Journal of the Korean Physical Society, 2015, 65(11): 1733–1737.
DOI:10.3938/jkps.65.1733( 0) 0)
|
| [4] |
LI Bai, LI Ya, GONG Ligang. Protein secondary structure optimization using an improved artificial bee colony algorithm based on AB off-lattice model[J]. Engineering Applications of Artificial Intelligence, 2014, 27(1): 70–79.
DOI:10.1016/j.engappai.2013.06.010( 0) 0)
|
| [5] |
DILL K A, BRONMBERG S, YUE K, et al. Principles of protein folding a perspective from simple exact models[J]. Protein Science, 1995, 4(4): 561–602.
DOI:10.1002/pro.5560040401( 0) 0)
|
| [6] |
LIANG Faming, WONG W H. Evolutionary Monte Carlo for protein folding simulations[J]. Journal of Chemical Phy-sics, 2001, 115(7): 3374–3380.
DOI:10.1063/1.1387478( 0) 0)
|
| [7] |
GUO Yuzhen, WANG Yong. Predicting the non-compact conformation of amino acid sequence by particle swarm optimization[C]//Proceedings of the 7th International Confe-rence on Systems Biology. Huangshan, China: IEEE, 23-25. DOI: 10.119/ISB.2013.6623805.
( 0) 0)
|
| [8] |
GARCI'A-MARTI'NEZ J M, GARZO'N E M, CECILIA J M, et al. An efficient approach for solving the HP protein folding problem based on UEGO[J]. Journal of Mathematical Chemistry, 2015, 53(3): 794–806.
DOI:10.1007/s10910-014-0459-1( 0) 0)
|
| [9] |
BAHI J M, CÔTE' N, GUYEUX C, et al. Protein folding in 2D Hydrophobic-hydrophilic square lattice model is chaotic[J]. Cognitive Computation, 2012, 4(1): 98–114.
DOI:10.1007/s12559-011-9118-z( 0) 0)
|
| [10] |
CRESCENZI P, GOLDMAN D, PAPADIMITRIOU C, et al. On the complexity of protein folding[J]. Journal of Computational Biology, 1998, 5(3): 423–465.
DOI:10.1089/cmb.1998.5.423( 0) 0)
|
| [11] |
GUO Yuzhen, WU Zikai, WANG Ying, et al. Extended particle swarm optimization method for folding protein on triangular lattice[J]. IET System Biology, 2016, 10(1): 30–33.
DOI:10.1049/iet-syb.2015.0059( 0) 0)
|
| [12] |
SU S C, LIN C J, TING C K. An effective hybrid of hill climbing and genetic algorithm for 2D triangular protein structure prediction[J]. Proteome Science, 2011, 9(Suppl 1): S19.
DOI:10.1186/1477-5956-9-S1-S19( 0) 0)
|
| [13] |
CITROLO A G, MAURI G. A local landscape mapping method for protein structure prediction in HP model[J]. Natural Computing, 2014, 13(3): 309–319.
DOI:10.1007/S11047-014-9427-8( 0) 0)
|
| [14] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Piscataway: IEEE, 1995, 4(8): 1942-1948. DOI: 10.1109/ICNN.1995.488968.
( 0) 0)
|
| [15] |
GUO Yuzhen. The non-compacted folding of proteins by modified elastic net algorithm[J]. Journal of Computational Biology, 2015, 22(7): 609–618.
DOI:10.1089/cmb.2012.0290( 0) 0)
|
 2017, Vol. 15
2017, Vol. 15


