近期,随着生命科学和计算机科学的快速发展,生物信息学作为一个新兴的交叉学科非常活跃。它通过综合利用生物学,计算机科学,应用数学和信息技术而揭示大量而复杂的生物数据所赋有的生物学奥秘。RNA在生命过程中起着非常重要的作用。许多实验已证实RNA的功能依赖于它本身的结构, 从RNA结构的角度探索RNA的功能是一个十分重要的研究课题, 因此RNA二级结构的相似性比较成为了这个课题的热点问题。随着基因组学和表观遗传学的发展,RNA在生命活动中所扮演的角色更加被科学家重视。通过对RNA结构相似性的分析,进而能够帮助我们了解RNA一些新的生物功能。同时,廖波、张屹和曹志等[1-3]在RNA二级结构比较上都做出了相应的贡献。
Liao等[1]给出了一种RNA二级结构的二元编码方法。文献[1]的做法是减少一个RNA二级结构分为三个二进制数字,并根据RNA二级结构的理化性质将编码的碱基分为三类,在提出编码规则的基础上进行操作,将X1异或X2用X1⊕X2表示。结合所提出的编码规则,得到两个特征序列所对应的两个RNA公共子序列二级结构,最终得到最优的对齐方式,通过这种方式可以判断碱基之间或者碱基对和碱基对之间的突变,并容易进行序列比对。Zhang等[2]比较RNA二级结构相似性并进行分类,提出了一种三维 (3D) 的RNA二级结构的图形表示,基于核酸的化学性质,把其中一个RNA二级结构首先转化为一个特征序列,然后构造一个动态的三维图的特征序列,最后用三维图的数值特征化代表RNA二级结构。进行RNA二级结构相似性分析。还有Cao等[3]提出了一种有效的方法。在突变分析的基础上进行引入的表示, 减少一个二级结构为三个二进制数字序列, 根据所提出的三维立方体表示,将介绍一个扩展的二进制编码方法的RNA二级结构进行调整,通过转换的结构比对到序列比对。之前,Yao等[4]在不同病毒图形表示的基础上,将RNA二级结构的相似性进行了一系列定量的比较。通过之前一些学者的经验理论,提出了一种新的表示方法。
本文主要介绍的是RNA二级结构的图形表示,并详细分析了RNA结构的表示方法, 利用其特点提出了RNA结构的表示方法---距离矩阵表示法, 在此基础上提出了基于距离矩阵表示法的相似性比对算法。主要内容包括如下几个方面:
(1) 介绍了生物信息学中一些最基本和最热点的问题。初步对RNA二级结构相似性问题有个大概的了解,同时对现阶段生物信息学的研究进展进行简单的分析。
(2) 提出一种新的RNA二级结构三维的图形表示方法。
(3) 根据定义的图形表示的性质,提取了九维特征向量代表选取的RNA二级结构序列。然后将算法运用到RNA相似性分析上,同时进行进化树分析,比较其相似性。
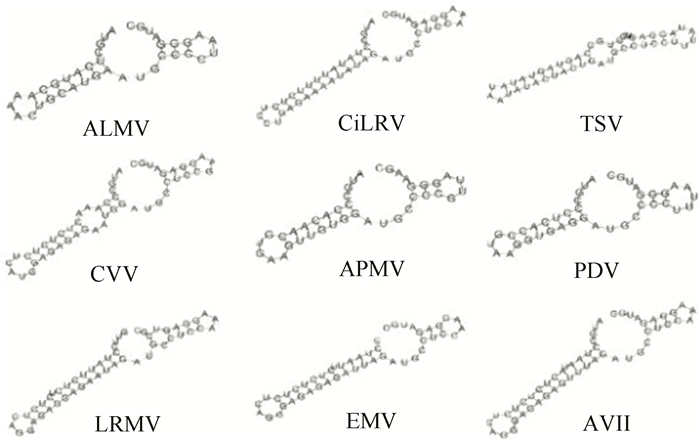
1 RNA二级结构的三维图形表示RNA二级结构是一组单碱基和碱基对通过氢键之间A-U, G-C的相互配对,相互作用形成一条RNA序列。根据RNA二级结构的特点,可以将一条RNA序列用碱基表示出来。图 1所示为本研究选取的九种病毒的RNA二级结构[5]。
|
图 1 九种病毒的RNA二级结构 Figure 1 RNA secondary structures of 9 viruses |
以其中一条为例,表示方法如下:
ALMV:AUGCUC’A’U’G’C’A’AAACU’G’C’A’U’G’A’AUGC’C’C’CUAAG’G’G’AUGC
从5’开始,A表示5’端开始,U为第二个碱基,依次类推,U’表示配对的碱基。根据这种规则可以得到一条用字母表示的RNA二级结构序列[6]。
RNA序列片段用这种方式表示后,选择三种表示方法将每一个碱基放在三维结构里进行定义,将每个碱基给予它一个点坐标。
根据以往Qi等[7]所提出的DNA序列三维图形表示,也相类似的进行RNA序列三维图形表示:将A, A’, C, C’, G, G’, U, U’分别置于+X轴、-X轴、+Y轴和-Y轴上,而特征曲线也是沿着+Z轴延伸。因此,依照以上分类方法,每条RNA序列都会得到三种不同的表示形式,用数学形式表示如下:设Y=y1y2...yn为任意的RNA序列,则存在三个映射fj, j=1, 2, 3,fj(Y)=fj(y1)fj(y2)…fj(yn).因此:
| $ \left( {\rm{i}} \right){\rm{ }}{f_1}({y_i}) = \left\{ \begin{array}{l} \left( {1, 0, i} \right), 若{y_i} = A/C;\\ \left( {0, 1, i} \right), 若{y_i} = A\prime /C\prime ;\\ \left( {-1, 0, i} \right), 若{y_i} = U/G;\\ \left( {0, -1, i} \right), 若{y_i} = U\prime /G\prime . \end{array} \right. $ | (1) |
| $ \left( {{\rm{ii}}} \right){\rm{ }}{f_2}({y_i}) = \left\{ \begin{array}{l} \left( {1, 0, i} \right), 若{y_i} = A/G;\\ \left( {0, 1, i} \right), 若{y_i} = A\prime /G\prime ;\\ \left( {-1, 0, i} \right), 若{y_i} = C/U;\\ \left( {0, -1, i} \right), 若{y_i} = C\prime /U\prime . \end{array} \right. $ | (2) |
| $ \left( {{\rm{iii}}} \right){\rm{ }}{f_3}({y_i}) = \left\{ \begin{array}{l} \left( {1, 0, i} \right), 若{y_i} = A/U;\\ \left( {-1, 0, i} \right), 若{y_i} = C/G;\\ \left( {0, 1, i} \right), 若{y_i} = A\prime /U\prime ;\\ \left( {0, -1, i} \right), 若{y_i} = C\prime /G\prime . \end{array} \right. $ | (3) |
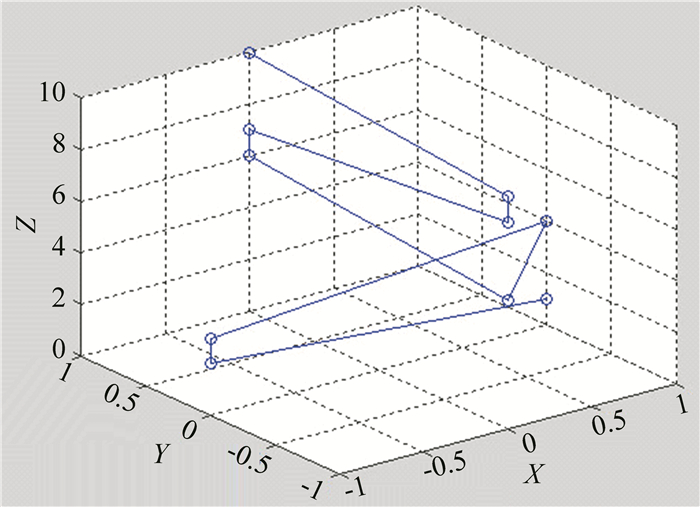
按照以上映射原则应用数学软件所画出的ALMV三维图 (见图 2).
|
图 2 RNA二级结构三维表示图 (以ALMV的子结构为例) Figure 2 3-D graphical representation of RNA secondary structures (Substructure of ALMV.) |
将RNA二级结构图形表示结束以后,进行相似性比较。通过上述方法得到这些点坐标之后,下一步,将计算这些点之间的距离。同时,当在计算各点之间的距离时也选取了三种方法,分别是:E矩阵,M/M矩阵和L/L矩阵[8]。计算方法如下:
(1) E矩阵: E中的元素eij即为曲线中的点i与点j之间的欧氏距离。
| $ {e_{ij}} = \sqrt {{{({x_{i1}}-{x_{j1}})}^2} + {{({x_{i2}}-{x_{j2}})}^2} + \cdot \cdot \cdot + {{({x_{in}}-{x_{jn}})}^2}} $ | (4) |
(2)M/M矩阵:其中 (i, j) 元由曲线上两个基对应点的欧式距离与它们之间存在的图论距离之比 (即|i-j|) 得到。
| $ 矩阵元素\left\{ \begin{array}{l} {m_{ij}} = \frac{{{e_{ij}}}}{{\left| {i-j} \right|}}{\rm{, }}若i \ne j;\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {m_{ij}} = 0, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 若i = j. \end{array} \right. $ | (5) |
(3)L/L矩阵:其中 (i, j) 元由曲线上两个基对应点的欧式距离与两点之间的距离总和之比得到。
| $ 矩阵元素\left\{ \begin{array}{l} {l_{ij}} = \frac{{{e_{ij}}}}{{\sum\limits_{k = i}^{j-1} {{e_{k(k + 1)}}} }}{\rm{, }}若i \ne j;\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {l_{ij}} = 0, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 若i = j. \end{array} \right. $ | (6) |
通过这三种方法,会得到三个最大特征值。因为开始进行RNA序列表示时就选取了三种表示方法,此时又选取了三种计算点之间距离的方法,所以,此刻会得到九个距离矩阵,因此就会有九个距离矩阵的最大特征值。
其中一个计算结果如下:
ALMV:E矩阵向量 (533.4072, 533.5630, 533.2587)
M/M矩阵向量 (40.2139, 40.5043, 40.2078)
L/L矩阵向量 (9.9845, 8.6573, 9.9938)
之后,将这些最大特征值组成一个向量,计算各向量间距离。向量之间的相似性,通过向量间的欧式距离进行计算,很明显,距离值越小,RNA二级结构序列的相似性就越高。计算结果见表 1。
| 表 1 E矩阵的上三角矩阵 Table 1 Upper triangular matrix of E matrix |
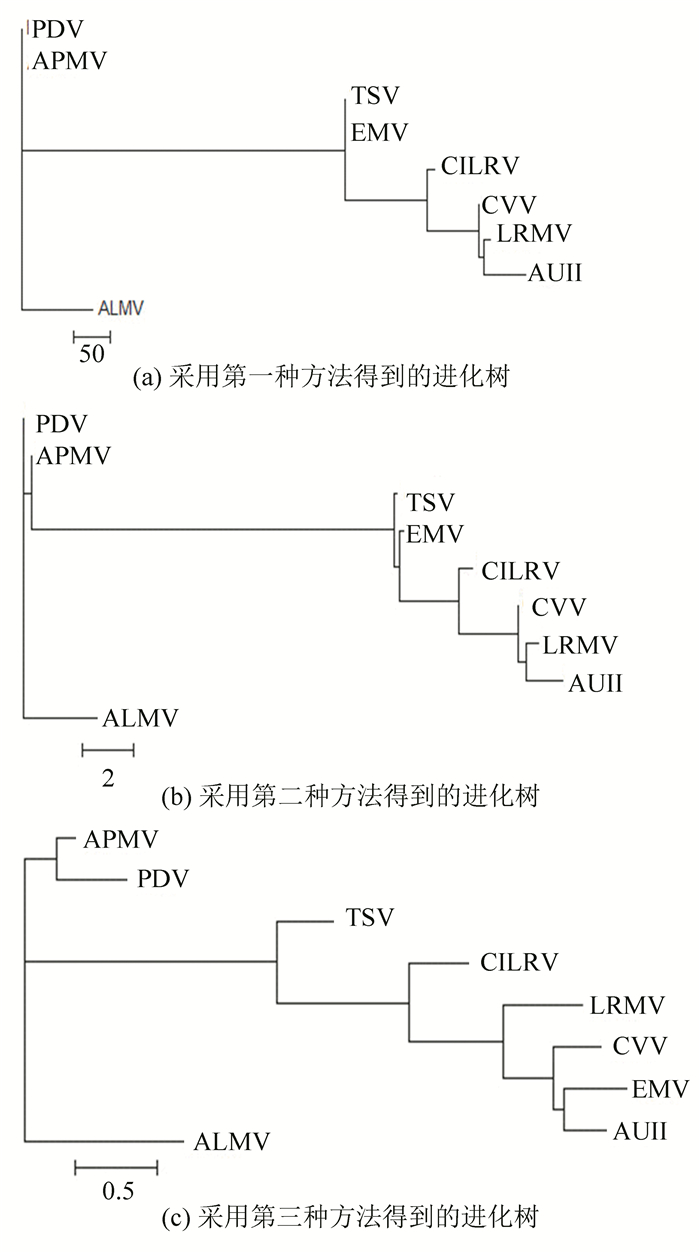
根据以上的结果,如果两条序列片段距离越小则越相似。最小距离法是在最小进化原理的基础上,构造一个距离矩阵来表示物种之间的进化距离。然后,通过这个距离矩阵,采用有效的方法将物种进行分类。然后进行系统进化树的构建,观察结果是否一致。在构建系统进化树时选取的是Neighbor-Joining方法。综上所述得出以下的结果,利用Phylip及MEGA软件描绘出系统进化树。三种方法得到三棵进化树如图 3所示。
|
图 3 根据进化距离所构建的系统进化树 Figure 3 Phylogenetic trees constructed according to the distance |
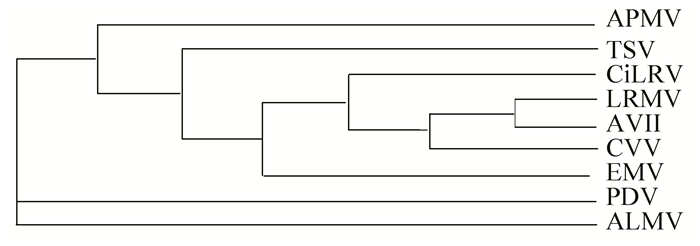
通过以上得到的三棵系统进化树之后,发现这三棵进化树并不完全一致,因此,有必要从这三棵进化树中提取它们的公共部分,也就是构建这三棵系统进化树的最大一致树 (见图 4),这样能综合三种图形表示方法的信息。Jansson等[9-10]在这方面开发出了很多算法,在这里应用多数一致树 (Majority consensus tree) 建立最大一致树。
|
图 4 根据三棵系统进化树构建的最大一致树 Figure 4 Maximum agreement tree is constructed by the three phylogenetic trees |
从这个系统进化树的图形表示中可以很清晰地看出,LRMV与AVII距离最近,说明这2种病毒RNA二级结构最为相似;同理,AVII与CVV相似性次之,等等。反之,APMV与ALMV的距离最远,则这两条序列相似性最弱。由此可见这九种病毒RNA二级结构的相似性程度。所采用的方法更为简便且直观。且与以往Liao等[11-12]的研究成果相似。文献[11-12]的研究结果表明:AVII, LRMV, EMV是最为相似的;同时,APMV, PDV与其他RNA二级结构之间是存在差异性的。由此可见,这一结果与本研究所得到的结果是相类似的。
3 讨论及结论对RNA二级结构与功能地研究是如今生物信息学一个十分重要的研究课题,但是对RNA结构相似性的预测分析仍然是很困难的。随着RNA结构相似性预测方法的日益发展,RNA数据库的不断增多,RNA结构预测的软件也日益增多。本文提出了一种新的RNA二级结构的图形表示方法。重点介绍了图形表示的构造,系统进化树的构建方法以及RNA二级结构序列间相似性的比较。根据所选取的图形表示方法,可以得到关于距离的特征值。随后,在这些距离特征值的基础上再利用预测软件构建系统进化树,基于这种方法,成功地提取了RNA二级结构相似性的一些基本信息。可见所选取的这种方法是可行的。
| [1] |
LIAO B, CHEN W, SUN X, et al. A binary coding method of RNA secondary structure and its application[J]. Journal of Computational Chemistry, 2009, 30(14): 2205–2212.
DOI:10.1002/jcc.21227 ( 0) 0)
|
| [2] |
ZHANG Y, HUANG H, DONG X, et al. A dynamic 3D graphical representation for RNA structure analysis and its application in non-coding RNA classification[J]. Plos One, 2016, 11(5): e0152238.
DOI:10.1371/journal.pone.0152238 ( 0) 0)
|
| [3] |
CAO Z, LIAO B, LI R, et al. RNA secondary structure alignment based on an extended binary coding method[J]. International Journal of Quantum Chemistry, 2011, 111(5): 978–982.
DOI:10.1002/qua.22464 ( 0) 0)
|
| [4] |
YAO Y, NAN X, WANG T. A class of 2D graphical representations of RNA secondary structures and the analysis of similarity based on them[J]. Journal of Computational Chemistry, 2005, 26(13): 1339–1346.
DOI:10.1002/jcc.20271 ( 0) 0)
|
| [5] |
LI Ying, DUAN Ming, LIANG Yanchun. Multi-scale RNA comparison based on RNA triple vector curve representation[J]. BMC Bioinformatics, 2012, 13(1): 280.
DOI:10.1186/1471-2105-13-280 ( 0) 0)
|
| [6] |
LIU Liwei, WANG Tianming. On 3D graphical representation of RNA secondary structures and their applications[J]. Journal of Mathematical Chemistry, 2007, 42(3): 595–602.
DOI:10.1007/s10910-006-9135-4 ( 0) 0)
|
| [7] |
QI Zhaohui, FAN Tongrang. PN-curve: A 3D graphical representation of DNA sequences and their numerical characterization[J]. Chemical Physics Letters, 2007, 442(4-6): 434–440.
DOI:10.1016/j.cplett.2007.06.029 ( 0) 0)
|
| [8] |
袁春欣. 核酸序列的图形表示理论及应用[D]. 大连: 大连理工大学, 2007.
YUAN Chunxin.Theory and application of graphical representation of nucleic acid sequences[D]. Dalian:Dalian University of Technology, 2007.
( 0) 0)
|
| [9] |
JANSSON J, SHEN C, SUNG W. Improved algorithms for constructing consensus trees[J]. Journal of the ACM, 2013, 63(3): 1800–1813.
( 0) 0)
|
| [10] |
JANSSON J, SHEN C, SUNG W. Algorithms for the majority rule (+) consensus tree and the frequency difference consensus tree[J]. Algorithms in Bioinformatics. Springer Berlin Heidelberg, 2013(8126): 141–155.
DOI:10.1007/978-3-642-40453-5_12 ( 0) 0)
|
| [11] |
LIAO B, WANG T M. A 3D graphical representation of RNA secondary structures[J]. Journal of Biomolecular Structure & Dynamics, 2004, 21(6): 827–32.
DOI:10.1080/07391102.2004.10506972 ( 0) 0)
|
| [12] |
LIAO B, WANG T, DING K. On a six-dimensional representation of RNA secondary structures[J]. Journal of Biomolecular Structure & Dynamics, 2005, 22(4): 1063–1071.
DOI:10.1080/08927020500371332 ( 0) 0)
|
 2017, Vol. 15
2017, Vol. 15


