2. 山东省肿瘤医院放疗病区,济南 250117
2. Department of Radiation Oncology, Shandong Cancer Hospital, Jinan 250117, China
原发性肝癌(Primary Liver Carcinoma, PLC)是我国常见的恶性肿瘤之一,尤其在南方地区患者甚广[1]。近年对中晚期原发性肝癌患者常采用精确放疗治疗方法,原发性肝癌患者精确放疗后易发生乙型肝炎病毒(Hepatitis B virus, HBV)再激活[2-3]。HBV再激活可影响患者的生存质量甚至缩短生存周期,找出HBV再激活的关键特征和构建HBV再激活预测模型对感染HBV的原发性癌患者具有重要研究意义。黄伟[4]等对69例经精确放疗的原发性肝癌患者研究发现,17例发生HBV再激活,其中3例死于HBV再激活,并找出了HBV DNA水平是影响HBV再激活的关键危险因素,即关键特征。在精确放疗过程中产生的临床数据集具有维度高、线性不可分等特点。因此,对于影响HBV再激活的关键特征有待进一步研究,HBV再激活的预测模型也亟需建立。
遗传算法[5-6](Genetic Algorithm, GA)已广泛应用于生物医学的特征选择方面,如基因微阵列数据[7-9]分类,蛋白质质谱数据[10]分析。GA的目的就是选择最优特征子集,GA的关键是选取合适的适应度函数得到最优特征子集,以达到较高的分类准确率, 本文选取基于经验分类错误率和后验概率的线性组合的适应度函数,选取出具有最优类别区分性的最优特征子集。
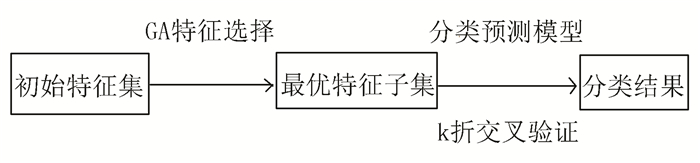
本文选取山东省肿瘤医院收治的90例原发性肝癌患者的临床数据作为研究,数据的初始特征集包含HBV DNA水平、肿瘤分期TNM、放疗剂量和DVH剂量体积等共28个初始特征。实验先采用GA从初始特征集选择不同规模的最优特征子集,然后采用Bayes和支持向量机(Support Vector Machine, SVM)建立HBV再激活的分类预测模型。分类过程中采用k折交叉验证(k-fold cross validation)方法选择出用于分类的训练样本和测试样本,并引入分类性能度量标准来评判特征选择以及分类器的效果,实验设计流程见图 1。
|
图 1 实验设计流程 Figure 1 Experimental design process |
GA把要解决的问题表示成带有编码的染色体,从种群中随机选取初代染色体作为父代,父代遵循适者生存、优胜劣汰机制,通过选择、交叉、变异操作产生适应新环境的子代染色体群,子代仍然遵循最适应环境产生下一代,这样每代不断进化后得到最适应环境的染色体,得到所求问题的最优解。本文将每个样本表示成n维特征空间中的一点,GA就是从n个特征中搜索出m个具有最优区分性的最优特征子集。
1.1.1 编码和解码GA的编码可分为二进制编码、符号编码、实数编码。依据本文数据为实数型和实数不需要编码和解码的特点,选用实数编码作为文中GA的编码,可直接进行最优目标值和适应值的计算。
1.1.2 适应度函数适应度函数[11]是寻找最优特征子集的关键,适应度的大小决定了个体的生存和消亡。好的适应度函数可以避免局部最优过早收敛和种群代数过慢结束。本文选取基于经验分类错误率和后验概率的线性组合的适应度函数,选取的特征子集具有较好的类别区分性,能够较准确地判定两种分类结果(HBV再激活与HBV未激活)。假设选取的2个特征子集I1和I2的经验分类错误率,若I1得到的后验概率P1大于I2得到的P2,则I1视作比I2更适应的个体。适应度函数公式如下:
| $ f\left( x \right) = 100{e_c} + {e_p} $ | (1) |
其中,ec为经验分类错误率,ep定义如下:
| $ {e_p} = 1 - \frac{1}{n}\left\{ {\sum\limits_{i = 1}^{{n_t}} {\max \left[ {P\left( {{c_1}\left| {{x_i}} \right.} \right), \cdots ,P\left( {{c_c}\left| {{x_i}} \right.} \right)} \right]} } \right\} $ | (2) |
式中nt表示训练样本数量,P(cj|xi)表示样本xi属于类cj的后验概率。
1.1.3 选择策略选择策略就是如何从父代群体中选取出那些个体作为下一代的遗传算子。为了保证群体的多样性,选取赌轮选择[12]方法作为选取下一代的选择策略,个体被选择的概率与其适应度大小成正比,定义与适应度成正比的概率函数ps(i):
| $ {p_s}\left( i \right) = \frac{{f\left( i \right)}}{{\sum\limits_{i = 1}^N {f\left( i \right)} }} $ | (3) |
其中,f(i)是个体i的适应度函数值;N为种群规模。用概率函数ps(i)组成面积为1的赌轮,赌轮转动时指针指向个体i所占面积的概率就是被选择的概率ps(i)。
1.1.4 交叉策略交叉策略是GA产生子代的主要方法,可将优秀的基因遗传给子代。均匀交叉[13]选为本文GA的交叉策略,均匀交叉先创建由1和0组成的向量,向量值为1时从父代P1得到一个基因,向量值为0时从父代P2得到一个基因,若向量组为[1 1 0 0 1 0 0 0],父代P1和P2为:
| $ \begin{gathered} P1 = \left[ {\begin{array}{*{20}{c}} a&b&c&d&e&f&g&h \end{array}} \right] \hfill \\ P2 = \left[ {\begin{array}{*{20}{c}} 1&2&3&4&5&6&7&8 \end{array}} \right] \hfill \\ \end{gathered} $ | (4) |
经交叉后得到子代C:
| $ C = \left[ {\begin{array}{*{20}{c}} a&b&3&4&e&6&7&8 \end{array}} \right] $ | (5) |
变异可以增加个体的多样性,常用均匀变异和高斯变异作为的GA的变异操作。均匀变异[14]从一定范围内均匀分布的随机数,用某一变异率来替换编码中某个基因位上的值。若染色体上第n个基因位的值为xn,在一个均匀范围[ln, un]内中产生一个随机数yn来替换xn。均匀变异公式定义为:
| $ {y_n} = \delta \left( {{l_n} - {u_n}} \right) + {x_n} $ | (6) |
δ是[0, 1]之间随机数。本文中设定的均匀变异的变异率为0.2。
1.1.6 种群规模种群规模的大小会影响GA的搜索能力,较大的种群规模可以提高搜索能力,但会增加GA的运算时间,较小的种群规模会降低GA的搜索能力,本文经验性的定义种群规模:
| $ N = n/m $ | (7) |
N为种群规模,n为初始特征集个数,m为特征子集规模,文中特征子集规模为1~6。
1.1.7 算法结束本文选取最大遗传代数作为算法的终止条件,如果当前遗传代数已经大于定义的最大遗传代数,则结束GA。
1.2 Bayes分类模型Bayes[15-16]判别分析是进行统计模式识别的重要方法。进行Bayes判别的数据要服从多元正态分布,其基本思想是根据先验概率分布求出后验概率分布。假定总体样本第k类样本的先验概率Pk,样品x属于k类样本的条件函数为fk(x),基于Bayes准则判别x属于k类样本的后验概率为:
| $ P\left( {k|x} \right) = \frac{{{P_k}{f_k}\left( x \right)}}{{\sum {{P_i}{f_i}\left( x \right)} }},i = 1,2, \cdots ,n $ | (8) |
Pi为第i个总体的先验概率;n为样本类别数量。其中,条件概率公式如下:
| $ {f_k}\left( x \right) = \left( {2{\pi }} \right) - \frac{e}{2}\left| {{V_k}} \right| - \frac{1}{2} \cdot \exp \left( { - \frac{{d_k^2\left( x \right)}}{2}} \right) $ | (9) |
Vk为联合协方差矩阵;dk2(x)为马氏距离;
选取后验概率值最大的归为第k类总体。
1.3 支持向量机模型支持向量机[17-19](Support Vector Machine, SVM)在结构风险最小化基础上发展而来,该算法在小样本数据集及高维数据模式识别中表现优秀。SVM寻找最优分类超平面,达到最优分类的同时最大化空白区域(margin),如图 2所示。

|
图 2 支持向量机 Figure 2 Support vector machine |
图中黑点和白点表示不同的两类样本,H为最优分类面上的直线。H1和H2与H平行,分别代表了两类样本与H最近距离的直线,两者之间的距离称为类间隔。
对于线性样本集(ai, bi),i=1, 2, …, n,a∈Rd, b∈[-1, +1]。利用Lagrange优化方法将最优分类问题转化为对偶问题,即在约束条件:
| $ \sum\limits_{i = 1}^n {{b_i}{\partial _i} = 0} $ | (10) |
和∂i≥0, i=1, 2, …, n的条件下,对∂i求下式的最大值:
| $ Q\left( \partial \right) = \sum\limits_{i = 1}^n {{\partial _i} - \frac{1}{2}\sum\limits_{i = 1}^n {{\partial _i}{\partial _j}{b_i}{b_j}\left( {{a_i} \cdot {a_j}} \right)} } $ | (11) |
其中∂i为每个样本对应的Lagrange算子,若∂i′为目标函数最优解,则解得最优分类函数为:
| $ f\left( a \right) = \operatorname{sgn} \left( {\sum\limits_{i = 1}^n {{\partial _i}^\prime {b_i}\left( {{a_i} \cdot a} \right) + c*} } \right) $ | (12) |
其中,c*为分类阈值。
SVM核函数可将非线性问题求解转化为线性问题求解。常用的核函数有:多项式核函数,RBF核函数,二层感知器核函数。本文转化过程采用RBF[20]核函数,对应函数为:
| $ K\left( {{x_i},{x_j}} \right) = \exp \left( { - \frac{{{{\left| {{x_i} - {x_j}} \right|}^2}}}{{{\delta ^2}}}} \right) $ | (13) |
定义三个分类性能度量[21]标准:
| $ 准确率 = \frac{{\left( {TP + TN} \right)}}{{\left( {TP + TN + FP + FN} \right)}} $ | (14) |
| $ 灵敏性 = TP/\left( {TP + FN} \right) $ | (15) |
| $ 特异性 = TN/\left( {TN + FP} \right) $ | (16) |
其中,TP, TN, FP和FN分别表示真阳性(HBV再激活),真阴性(HBV未激活),假阳性和假阴性样本的数量,分类准确率作为判断分类性能的主要标准。
1.5 交叉验证实验统计结果选择k折交叉验证[22-23](k-fold cross validation),把样本n分为k份不相同的子集样本,m=n/k,m为每份的容量。定义nk为第k份子集样本(k=1, 2, …, n),从样本n中选取子集样本nk作为测试样本,其余子集样本作为训练样本。预测结果为k折交叉验证结果的平均
| $ {{\hat u}_k} = \frac{1}{k}\sum\limits_1^k {{u_k}} $ | (17) |
本文交叉验证的k值取10。
2 实验结果与分析实验数据共含有90个样本,每个样本包含28个特征对应的特征值,20例样本发生HBV再激活,70例样本未激活。
实验分为2个部分:特征选择和分类。首先运行GA来选择最具区分性的特征子集,最优特征子集规模为1~6。使用Bayes和SVM分别对最优特征子集和初始特征集进行分类预测,为了得到更加稳定准确的结果,运行10次10折交叉验证。为了公正的评价GA特征选择的性能,重复运行GA50次。实验选取准确率最高的特征子集,具体实验结果详见下列表格。
最优特征子集规模为1~6时和初始特征集的Bayes与SVM实验结果如表 1、表 2所示。
| 表 1 Bayes实验结果 Table 1 Experimental results of Bayes |
| 表 2 SVM实验结果 Table 2 Experimental results of SVM |
从表 1、表 2的最优特征子集与初始特征集对比中我们可以看出,不同规模的最优特征子集的分类性能不同。表 1的最优特征子集规模为5并选取9, 6, 7, 17, 27时的分类性能最优,准确率从70.00%提高到82.89%,灵敏性从75.00%提高到84.52%,特异性从52.49%提高到75.38%。表 2最优特征子集规模为5选取9, 6, 7, 17, 27时的分类性能最优,准确率从72.22%提高到83.34%,灵敏性从76.06%提高到85.77%,特异性从57.89%提高到74.82%。对比表 1和表 2实验结果的准确率、灵敏性和特异性都表明了:两种分类预测模型对HBV再激活的判断都有着良好的识别能力,而且初始特征集的分类性能都较低,经GA特征选择后的最优特征子集的分类性能明显得到提高。
由上表 1、表 2可知最优特征子集规模为5时选取的特征子集具有最显著类区分性。分别用Bayes和SVM对特征子集规模为5的特征子集进行分类性能预测,这些特征子集的准确率都达到80%以上,且SVM准确率达到80%以上的特征子集更多。实验结果详见表 3和表 4。
| 表 3 特征子集规模为5的Bayes实验结果 Table 3 Experimental results of Bayes when the feature subsets are 5 |
| 表 4 特征子集规模为5的SVM实验结果 Table 4 Experimental results of SVM when the featuresubsets are 5 |
所有的特征子集里面存在共同的特征9代表了HBV DNA水平,已经被文献[24]证明是影响HBV再激活的独立危险因素, 即关键特征子集,但未建立HBV再激活的预测模型。文献[25]通过logistic回归分析,找出HBV DNA水平,肿瘤分期TNM和外放边界是影响HBV再激活的3个危险因素,建立了基于神经网络的HBV再激活预测模型,识别率达到80.00%。同样,本文将遗传算法特征选择用于HBV数据集当中3个危险因素也都在GA的特征选择当中出现,证明了GA在本文的可行性,且两种分类模型的分类性能也更优秀,尤其当特征子集规模为5并选取9, 6, 7, 17, 27时,Bayes与SVM的分类性能最优分别达到82.89%和83.34%。选择的特征子集更多,分类预测模型分类识别率较之前有提高,这证明了基于遗传算法特征选择的可行性与两种分类器的优秀分类能力。
频繁出现的特征编号及其所代表的医学参数详见表 5。
| 表 5 特征编号及其代表的医学参数 Table 5 Feature numbers and medical parameter |
这些医学参数对HBV再激活有着重要影响,在病人治疗过程中密切注意医学参数的变化,提前采取抗病毒及肝保护治疗方法,减少HBV再激活的发生,可提高病人的生活质量甚至生存周期。
特征子集规模为5并选择的特征为9, 6, 7, 17, 27时,即分别代表特征:HBV DNA水平,肿瘤分期TNM,Child-Pugh,外放边界和全肝最大剂量时的分类准确性达到最优。用Bayes和SVM分别对以上5个特征进行分类性能预测,以分类准确率作为HBV再激活贡献度大小,详见表 6。
| 表 6 单个特征的分类性能 Table 6 The contribution of a single feature |
5个特征对HBV再激活贡献度从大到小分别为:HBV DNA水平>肿瘤分期TNM>外放边界>Child-Pugh>全肝最大剂量。
3 结束语本文提出将遗传算法的特征选择用于复杂的原发性肝癌数据上,对原发性肝癌初始特征集进行不同规模的特征选择,选择的特征HBV DNA水平、肿瘤分期TNM和外放边界从先前研究者的论文中已经得到证实,充分表明了本文将遗传算法的特征选择用于原发性肝癌数据集可行性和有效性。建立的Bayes和SVM分类预测模型具有较强的模式识别能力,并且经GA特征选择后的最优特征子集分类性能明显提高,尤其当特征子集规模为5,选择的特征为:HBV DNA水平,肿瘤分期TNM,Child-Pugh,外放边界和全肝最大剂量时的分类性能达到最优。并且,对HBV再激活的贡献率从高到低排序分别为: HBV DNA水平>肿瘤分期TNM>外放边界>Child-Pugh>全肝最大剂量。
实验表明基于遗传算法的特征选择方法以及两种预测模型在HBV再激活预测中具有较高的应用价值,在病人进行治疗过程中,可同时监控多个医学参数的变化,尤其是对已经感染HBV但未发生HBV激活的原发性肝癌患者,提前采取抗病毒以及肝保护等治疗方法,减少HBV再激活的发生,对提高患者的生活质量甚至延长生存周期有着重要意义。今后将继续研究其他智能算法在HBV再激活的应用,致力于提高HBV再激活的分类性能。
| [1] |
LUO R H. Risk factors for primary liver carcinoma in Chinese population[J]. World Journal of Gastroenterology, 2005, 11(28): 4431–4434.
DOI:10.3748/wjg.v11.i28.4431 ( 0) 0)
|
| [2] |
JI H K, PARK J W, KIM T H, et al. Hepatitis B virus reactivation after three-dimensional conformal radiotherapy in patients with hepatitis B virus-related hepatocellular carcinoma[J]. International Journal of Radiation Oncology Biology Physics, 2007, 69(3): 813–819.
DOI:10.1016/j.ijrobp.2007.04.005 ( 0) 0)
|
| [3] |
PARK J W, JI H K, KIM T H. In reply to dr. Cheng[J]. International Journal of Radiation Oncology Biology Physics, 2008, 71(3): 961–962.
DOI:10.1016/j.ijrobp.2008.02.041 ( 0) 0)
|
| [4] |
黄伟, 卢彦达, 张炜, 等. 原发性肝癌精确放疗致乙型肝炎病毒再激活分析[J]. 中华放射肿瘤学杂志, 2013, 22(3): 193–197.
HUANG Wei, LU Yanda, ZHANG Wei, et al. Analysis of hepatitis B virus reactivation induced by precise radiotherapy in patients with primary liver cancer[J]. Chinese Journal of Radiation Oncology, 2013, 22(3): 193–197.
DOI:10.3760/cma.j.issn.1004-4221.2013.03.006 ( 0) 0)
|
| [5] |
LIU Y, AICKELIN U, FEYEREISL J, et al. Wavelet feature extraction and genetic algorithm for biomarker detection in colorectal cancer data[J]. Knowledge-Based Systems, 2013, 37(2): 502–514.
DOI:10.1016/j.knosys.2012.09.011 ( 0) 0)
|
| [6] |
KARAKIŞ R, TEZ M, KILIÇ Y A, et al. A genetic algorithm model based on artificial neural network for prediction of the axillary lymph node status in breast cancer[J]. Engineering Applications of Artificial Intelligence, 2013, 26(3): 945–950.
DOI:10.1016/j.engappai.2012.10.013 ( 0) 0)
|
| [7] |
LIU Y. Prominent feature selection of microarray data[J]. Progress in Natural Science, 2009, 19(10): 1365–1371.
DOI:10.1016/j.pnsc.2009.01.014 ( 0) 0)
|
| [8] |
LIU Y. Detect key gene information in classification of microarray data[J]. Journal on Advances in Signal Processing, 2008, 2008(1): 1–10.
DOI:10.1155/2008/612397 ( 0) 0)
|
| [9] |
LIU Yihui, BAI Li. Find significant gene information based on changing points of microarray data[J]. IEEE Transactions on Biomedical Engineering, 2009, 56(4): 1108–1116.
DOI:10.1109/TBME.2008.2009543 ( 0) 0)
|
| [10] |
李义峰, 刘毅慧. 基于遗传算法的蛋白质质谱数据特征选择[J]. 计算机工程, 2009, 35(19): 192–197.
LI Yifeng, LIU Yihui. Feature selection for protein mass spectrometry data based on genetic algorithm[J]. Computer Engineering, 2009, 35(19): 192–197.
( 0) 0)
|
| [11] |
桑君.基于遗传算法和线性分类器的31P磁共振波谱肝癌诊断[D].济南:山东轻工业学院, 2010.
SANG Jun. Diagnosis of 31Phoshorusmagnetic resonance liver cancer data based on genetic algorithm and linear classifier[D]. Jinan: Shandong Institute of Light Industry, 2010.
( 0) 0)
|
| [12] |
胡新平, 贺玉芝, 倪巍伟, 等. 基于赌轮选择遗传算法的数据隐藏发布方法[J]. 计算机研究与发展, 2012, 49(11): 2432–2439.
HU Xinping, HE Yuzhi, NI Weiwei, et al. A privacy-preserving data publishing method based on genetic algorithm with roulette wheel[J]. Journal of Computer Research and Development, 2012, 49(11): 2432–2439.
( 0) 0)
|
| [13] |
熊军, 高敦堂, 沈庆宏, 等. 遗传算法交叉算子性能对比研究[J]. 南京大学学报(自然科学), 2004, 40(4): 432–437.
XIONG Jun, GAO Duntang, SHEN Qinghong, et al. Comparation of Crossover Operators in Genetic Algorithm[J]. Journal of Nan Jing University (Natural Sciecne), 2004, 40(4): 432–437.
DOI:10.3321/j.issn:0469-5097.2004.04.005 ( 0) 0)
|
| [14] |
JOSEPH N P, RAMADOSS B. A Genetic algorithm applying single point crossover and uniform mutation to minimize mncertainty in production cost[J]. World Applied Sciences Journal, 2013, 23(8): 1013–1017.
DOI:10.5829/idosi.wasj.2013.23.08.956 ( 0) 0)
|
| [15] |
廖小波.基于贝叶斯最优统计的图切法图像分割研究[D].昆明:昆明理工大学, 2015.
LIAO Xiaobo. The research about graph cuts in image segmentation based on Bayesian optimal statistics[D].Kunming: Kunming University of Science and Technology, 2015.
http://cdmd.cnki.com.cn/Article/CDMD-10674-1015641429.htm ( 0) 0)
|
| [16] |
邹永斌, 陈兴蜀, 王文贤. 基于贝叶斯分类器的主题爬虫研究[J]. 计算机应用研究, 2009, 26(9): 3418–3420.
ZOU Yongbin, CHEN Xingshu, WANG Wenxian. Research on focused crawler based on Bayes classifier[J]. Application Research of Computers, 2009, 26(9): 3418–3420.
DOI:10.3969/j.issn.1001-3695.2009.09.061 ( 0) 0)
|
| [17] |
FUREY T S, CRISTIANINI N, DUFFY N, et al. Support vector machine classification and validation of cancer tissue samples using microarray expression data[J]. Bioinformatics, 2001, 16(10): 906–914.
DOI:10.1093/bioinformatics/16.10.906 ( 0) 0)
|
| [18] |
NOBLE W S. What is a support vector machine? Nat Biotechnol[J]. Nature Biotechnology, 2007, 24(12): 1565–1567.
DOI:10.1038/nbt1206-1565 ( 0) 0)
|
| [19] |
BOVOLO F, BRUZZONE L, CARLIN L. A novel technique for subpixel image classification based on support vector machine[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2010, 19(11): 2983–2999.
DOI:10.1109/TIP.2010.2051632 ( 0) 0)
|
| [20] |
LIU Yihui. Feature extraction and dimensionality reduction for mass spectrometry data[J]. Computers in Biology & Medicine, 2009, 39(9): 818–823.
DOI:10.1016/j.compbiomed.2009.06.012 ( 0) 0)
|
| [21] |
李义峰.基于优化算法的蛋白质质谱数据分析[D].济南:山东轻工业学院, 2009.
LI Yifeng. Optimizationalgorithms based protein mass spectrometry data analysis[D]. Jinan: Shandong Institute of Light Industry, 2009.
http://cdmd.cnki.com.cn/Article/CDMD-10431-2009219663.htm ( 0) 0)
|
| [22] |
FUSHIKI T. Estimation of prediction error by using K-fold cross-validation[J]. Statistics & Computing, 2011, 21(2): 137–146.
DOI:10.1007/s11222-009-9153-8 ( 0) 0)
|
| [23] |
HASSEIM A A, SUDIRMAN R, KHALID P I. Handwriting classification based on support vector machine with cross validation[J]. Engineering, 2013, 05(5): 84–87.
DOI:10.4236/eng.2013.55B017 ( 0) 0)
|
| [24] |
WEI H, WEI Z, MIN F, et al. Risk factors for hepatitis B virus reactivation after conformal radiotherapy in patients with hepatocellular carcinoma[J]. Cancer Science, 2014, 105(6): 697–703.
DOI:10.1111/cas.12400 ( 0) 0)
|
| [25] |
WU Guanpeng, WANG Shuai, HUANG Wei, et al. Application of BP and RBF neural network in classification prognosis of hepatitis B virus reactivation[J]. Journal of Electrical and Electronic Engineering, 2016, 4(2): 35–39.
DOI:10.11648/j.jeee.20160402.16 ( 0) 0)
|
 2016, Vol. 14
2016, Vol. 14


