2. 西安财经学院信息学院,西安 710100
2. School of Information, Xi’an University of Finance and Economics, Xi’an 710100,China
With the development of synthetic biology,it has become necessary to develop tools andmethodologies to streamline the design of custom genetic constructs[1]. Gene expression studies,gene network studies,protein expression vector design and metabolic engineering are some of applications of this technology [2-3]. GenoCAD is a web-based application to fill the needs of these scientific studies. It is built upon a solid computational linguistic foundation and can be used to design synthetic genetic constructs[4]. Yet,its point and-click graphical user interface enables users to design complex constructs in a matter of minutes. GenoCAD captures design strategies of synthetic genetic constructs in the form of grammatical models [5]. It provides a central parts database with each grammar,and the latest GenoLIB grammar comes with a library of 1943 basic genetic parts that come from 2 000 widely used plasmids [6]. As proof,the library was converted into GenoCAD grammar files to allow users to import and customize the library based on the needs of their research projects. Users,who elect to create a GenoCAD personal account,can log in the system to create project-specific parts libraries,upload new parts into their workspace and save designs for later use [5]. Thinking of genetic systems as composed of parts,each with its own function and characteristics,is the design philosophy of GenoCAD. Promoters,ribosome-binding sites (RBS),genes and terminators are all categories of parts that are needed for designing complex genetic constructs[7-9] in GenoCAD. Decomposing biological sequences into functional modules as genetic parts is one of the ways to update the GenoCAD library[6].
When researchers assembling more than a few specific genetic parts from different categories,the process is always costly,time consuming and error prone. In order to streamline this process,some assemblystandards are introduced. The BioBrick Foundation (BBF) has been instrumental in promoting the BioBrick standard. A BioBrick compliant part is a DNA fragment flanked by a prefix and a suffix sequence having specific restriction sites[10-11]. Two BioBrick parts can be assembled by using a specific series of restriction digestions and ligations independent of the parts sequences. Theoretically,any set of genetic parts compliant with the same standard can be assembled by using specific restriction and ligation enzymes. In order to reduce the time and cost of assembling,researchers and engineers develop robotic platforms that can help automate the process of assembling many multi-kilobase genetic constructs. The determination of an optimal assembly process can be totally automated by dynamic programming algorithms without thinking of experience[12]. In GenoCAD design,a user can design a synthetic construct by successively selecting design rules to transform the structure of the design. At last select specific parts to complete the design [13]. But more and more genetic parts are imported into GenoCAD. Now,users are always puzzled to choose a suitable part from few sets of categories in the last step of a design. To overcome this,statistical language model (SLM) is introduced in this paper which can help streamline the process of design. The first goal of SLM is to build a statistical language model that can estimate the distribution of natural language as accurate as possible[14]. The original (and is still the most important) application of SLMs is speech recognition,but SLMs also play a vital role in various other natural language applications as diverse as machine translation,part-of-speech tagging,intelligent input method and Text To Speech system. The statistical language model in this paper is based on the statistical parameters coming from BioBrick standard parts. After transforming the design process into this mathematic model,a dynamic programming algorithm can be carried out to choose suitable parts composing the final genetic construct. The algorithm takes experience of former iGEM design into account to reduce the cost,time and errors of the assembling process. This method can not only optimize the result of GenoCAD design but also can help design new projects by considering former experience.
2 Materials and methodsWe use link http://parts.igem.org/das/parts/entry_points/ to download the entry points to the parts that we want to analyze in June 2014. The version of this file published at that time included 7 242 parts. A Perl script was developed to parse out the content of each part from the link http:// parts.igem.org/das/parts/features/?segment=part#. And decomposed them into structured data format,which could be imported into a MySQL database. After imported into a MySQL database,75 744 features were parsed out from these parts. The parts include both basic parts (e.g. promoter and RBS) and composed parts,which include multiple basic parts (e.g. device,project and composite). The basic parts include categories of Regulatory,RBS,Coding,Terminator and Plasmid Backbone. We queried the MySQL database to extract the basic parts and counted their usage in composed parts. We also developed Perl script and SQL sentences to analyze composed parts and counted the usage of two adjacent basic parts (parts pair) in them. By querying the MySQL database,we extracted a set of 1 682 basic parts compliant with RFC 23 standard[15]. It means that the sequence of these basic parts does not include any of the restriction sites used by the assembly standard. These 1 682 basic parts include 405 promoters,42 RBSs,57 terminators and 1 178 genes. We imported these basic parts into GenoCAD to design new genetic constructs. And the usage frequencies of basic parts and the usage frequencies of parts pair in the dataset can be calculated.
3 Grammar design in GenoCADThe general methodology of developing grammarsin GenoCAD to model the structure of synthetic genetic constructs has been described detailedly before[4, 16].The grammar used in this article is similar to the context-free grammar (CFG)[16],but has new rewriting rules to allow protein fusion. We used biobrick_icon_set to represent the categories of basic parts. The full grammar is described in Table 1.
| Table 1 The grammar used in this paper |
At the last step of GenoCAD design,every icon has its option. It is somewhat difficult for designer to choose the most suitable part to finish the design (Fig. 1). To overcome this,statistical language model (SLM) is introduced. In this model,whether a sentence (S) is meaningful and reasonable is based on the probability it will happen. A sentence (S) is composed of a sequence of words. Here S is a genetic construct designed in GenoCAD and the words are imported basic parts. Now,S = part1,part2,…,partn and we need to know its P(S)---the probability it will happen.
| $P\left( S \right)=P(par{{t}_{1}},par{{t}_{2}},...,par{{t}_{n}})$ | (1) |
According to conditional probability formula
| $\begin{align} & P\left( par{{t}_{1}},par{{t}_{2}},...par{{t}_{n}} \right)= \\ & P(par{{t}_{1}})\cdot P(par{{t}_{2}}par{{t}_{1}})\cdot \\ & P(par{{t}_{3}}par{{t}_{1}},par{{t}_{2}})\cdots \cdots \\ & P(par{{t}_{n}}par{{t}_{1}},par{{t}_{2}},\cdots ,par{{t}_{n-1}}) \\ \end{align}$ | (2) |
In formula 2,P(part1) means the probability part1 appears in the design. P(part2︱part1) means the probability that part2 appears with part1 prior to it. According to formula 2,the probability partn appears is determined by all the parts appear prior to it. The P(part1) and P(part2︱part1) are easy to calculate,but calculating P(part3︱part1,part2) is not easy. And calculating P(partn︱part1,part2,…,partn-1) is very difficult,because much more variables are involved in. The conditions are too complex to gauge. Based on Markov Hypothesis we think the probability a part appear is only concerned with the part prior to it.
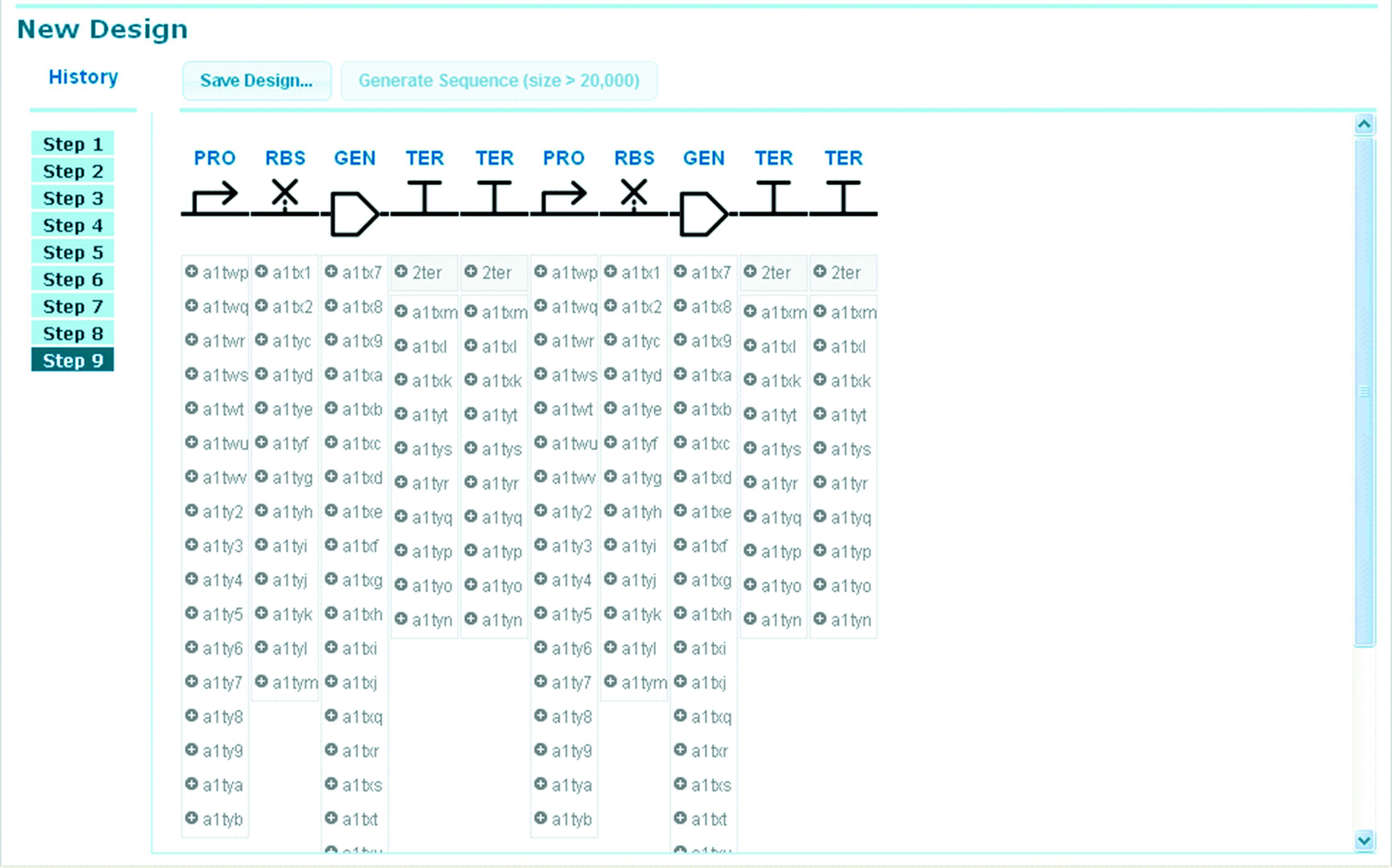
|
Figure 1 At the last step,it’s always difficult to choose a suitable part |
So formula 2 can be simplified as
| $\begin{align} & P\left( S \right) \\ & =P(par{{t}_{1}})\cdot P(par{{t}_{2}}par{{t}_{1}})\cdot \\ & P(par{{t}_{3}}par{{t}_{2}})\cdots \cdots P(par{{t}_{i}}par{{t}_{i-1}})\cdots \cdots \\ & P(par{{t}_{n}}par{{t}_{n-1}}) \\ \end{align}$ | (3) |
NowP(S) ---the probability a S will happen can be calculated. Formula 3 is the Bigram Model of statistical language model. Then according to conditional probability formula
| $P(par{{t}_{i}}par{{t}_{i-1}})=\frac{P(par{{t}_{i*1}},par{{t}_{i}})}{P(par{{t}_{i-1}})}$ | (4) |
We use usage frequencies of two adjacent basic parts (parts pair) and usage frequencies of basic parts to estimateP (parti-1,parti) and P(parti-1) respectively.
| $\begin{align} & P\left( par{{t}_{i-1}},par{{t}_{i}} \right)\approx \frac{Count\left( par{{t}_{i-1}},par{{t}_{i}} \right)}{Count\left( all\_parts \right)} \\ & P(par{{t}_{i-1}})\approx \frac{Count(par{{t}_{i-1}})}{Count\left( all\_parts \right)} \\ & And\text{ }P(par{{t}_{i}}par{{t}_{i-1}})\approx \frac{Count(par{{t}_{i-1}},par{{t}_{i}})}{Count(par{{t}_{i-1}})} \\ \end{align}$ | (5) |
In this way any component in formula 3 can be calculated.
At the last step of design (Fig. 1),there are too many combinations of basic parts to finish the design. Which one is the most reasonable and meaningful? We think the one with the largest appearing probability is. We have all the candidate paths,and a path will result a S (a path = a S = part1,part2,…,partn). The best path is represented with PATH.
| $PATH=\underset{all\_S}{\mathop{argmax}}\,\left( P\left( S \right) \right)$ |
To avoid memory overflow when performing algorithm in computer,we take the log of P(S).
| $\begin{align} & PATH \\ & =\underset{all\_S}{\mathop{argmax}}\,(logP\left( S \right)) \\ & =\underset{all\_S}{\mathop{argmax}}\,(log(P(par{{t}_{1}})\times \prod\limits_{i=2}^{n}{P}(par{{t}_{i}}par{{t}_{i-1}}))) \\ & =\underset{all\_S}{\mathop{argmax}}\,(logP(par{{t}_{1}})+\sum\limits_{i=2}^{n}{logP}(par{{t}_{i}}par{{t}_{i-1}})) \\ \end{align}$ | (6) |
According to formula 5,we got formula 7 and 8
| $P(par{{t}_{i}}par{{t}_{i-1}})=\frac{Count(par{{t}_{i-1}},par{{t}_{i}})}{Count(par{{t}_{i-1}})}$ | (7) |
| $P(par{{t}_{1}})=\frac{Count(par{{t}_{1}})}{Count\left( all\_parts \right)}$ | (8) |
Because we extracted the dataset from a relatively sparse corpus,the zero-frequency problem would arise when parts pair never occurred in the training corpus. To overcome this,we use Add-one (Laplace) Smoothing[17]. So formula 7 should be
| $P(par{{t}_{i}}par{{t}_{i-1}})=\frac{Count(par{{t}_{i-1}},par{{t}_{i}})+1}{Count(par{{t}_{i-1}})+N}$ | (9) |
In formula 9 N is the number of Bigram (parts pair). Formula 8 and 9 will be used to fill the corresponding component in formula 6. The resulted PATH will be the S with the largest appearing probability in all candidate paths. And we will use dynamic programming algorithm to select the PATH from all candidates.
5 AlgorithmNow we need to find a path in the lattice in Fig. 1. This path is composed of series of parts and will be the S with the largest probability. It means how we can solve formula 6. The algorithm originates from the Viterbi algorithm[18] and will consist of three steps.
Firstly,build a candidate lattice.Every icon (category) corresponds to one column,and every node in a column corresponds to a basic part. At the start and end of the lattice,BEG and END columns were added. In these two columns,two virtual nodes of B and E were added respectively (Fig. 2). Every node is a triple-tuple < name,V,P>,and the first element name was filled with basic part name.
Secondly,fill the lattice.In the lattice from left to right,for every node of a triple-tuple < name,V,P>,the V and P are calculated and filled. V will be filled with the maximum value selected from combining operation of two nodes in adjacent columns. P will store the address of the node prior to it where V comes from via combining operation.
1) The first column,for the B node let V= 0 and P= NULL.
2) The second column,every node < name,V,P> (name∈{I0500,R0011,… ,R0040,…}) will combine with B node and calculate its V and P.
V=VB+logP(part)=logP(part)
P=address_of_B
3) The third column,every node <name,V,P > (name∈{R0032,R0034,… ,R0041,…}) will combine with every node in the second column and calculate its V and P.
V=max{Vprior+logP(partpartprior)}
P=address_where_V_comes_from
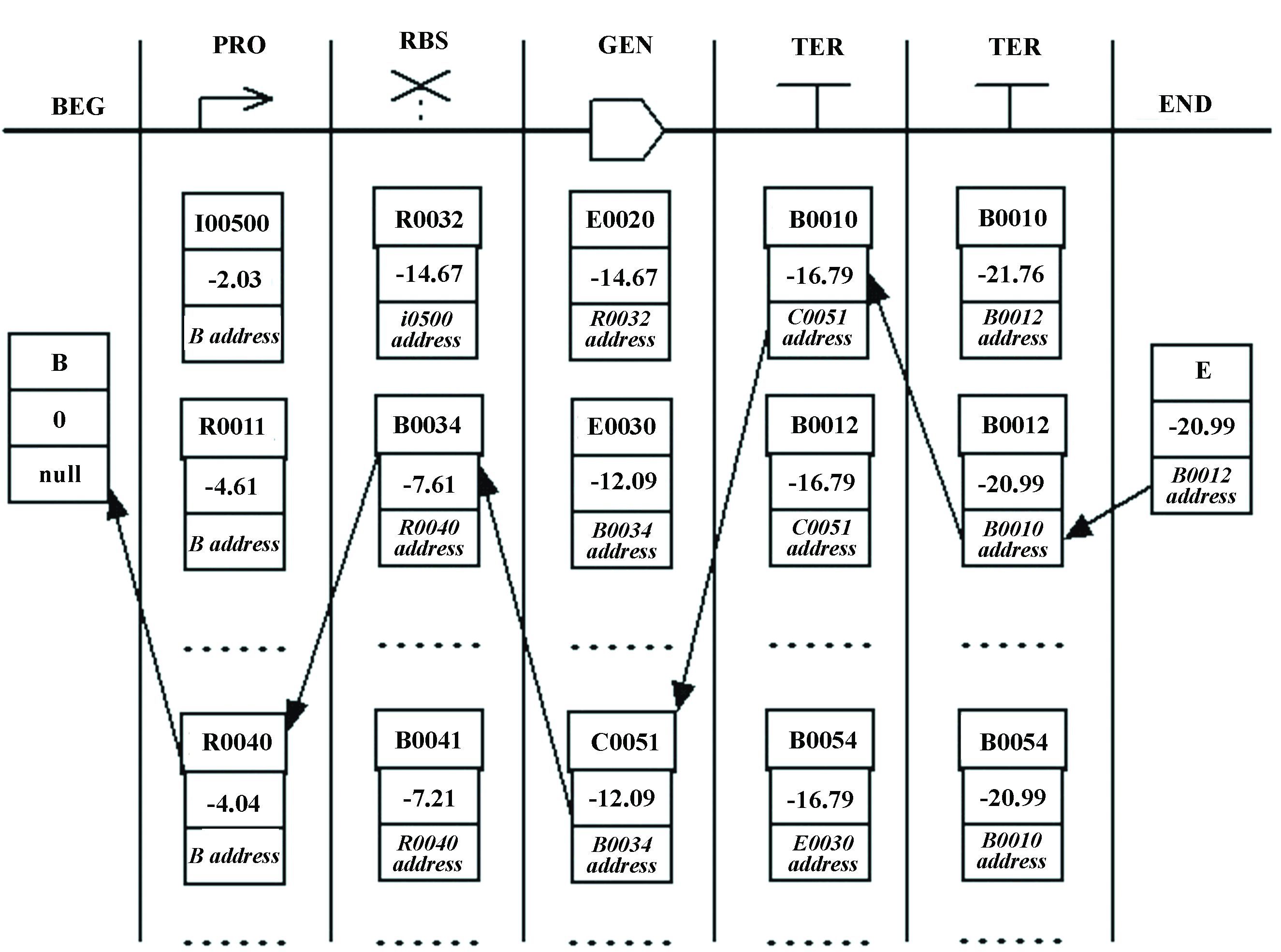
|
Figure 2 The process of building lattice,filling lattice,and recalling |
4) Repeat 3) ,every node in current column will combine with every node in prior column and calculate its V and P.
5) In the END column,V is the maximum value selected from the nodes in prior column,P will store the address of the node where V comes form.
Thirdly,recall and get thePATH. Start from node E,search the P prior to it continually (Fig. 2).
Finally,the PATH with the largest probability will be found and the resulted S is the optimized genetic construct. If the length of S is L and the maximum node number in a column is D,the algorithm complexity of this algorithm will be O(L·D2),and the algorithm complexity of exhaustive algorithm is O(DL).
6 ResultsTo demonstrate how to optimize a GenoCAD design,we selected the banana odor biosynthetic system (http://parts.igem.org/Part:BBa_J45900) designed and implemented by the MIT iGEM team in 2006. The system contains two expression cassettes: one with BAT2 and THI3 genes produces isoamyl alcohol,and the second one catalyzes the conversion of the cellular metabolite leucine to isoamyl acetate or banana odor. We design the system according to the grammar described previously. At the last step,we need to choose suitable basic parts to finish the design (Fig. 3). After the genes we want to express are determined,the optimizing algorithm will be implemented by a Perl script. At the first round of implementing algorithm,it recommended the parts series R0040-B0034-J45008-B0030-J45009-R0040-B0034-J45014-B0010-B0012. At the second round,when we excluded RBS B0034,the algorithm recommended the series R0040-B0030-J45008-B0030-J45009-R0040-B0030-J45014-B0010-B0012. At the third round,when we excluded promoter R0040 in the first column,the algorithm recommended the series R0011-B0030-J45008-B0030-J45009-R0040-B0030-J45014-B0010-B0012. And this is the real parts what banana odor biosynthetic system consists of. When we develop new project and carry out the algorithm at the last step,the algorithm will give out an optimized result based on experience. If we need some other options,we can exclude some parts and repeat the algorithm. It will recommend some other optimized results for consideration. If we have known that some parts are definitely connected,we can determine them first then implement the algorithm.

|
Figure 3 The last step of designing the banana odor biosynthetic system |
This article has presented a statistical language model for synthetic biological parts assembling.After converting the BioBrick parts assembly process into a Bigram Model,a dynamic programming algorithm can be carried out to select an optimized result. The algorithm can be iterated then gives out different optimized results for consideration,but it can still not be embedded into other software. The method can be not only used to optimize a design in a synthetic biological robotic platform such as GenoCAD,but also independently used to automate the DNA assembly process in synthetic biology. After inputting categories of synthetic biological parts according to a grammar,the algorithm automatically assemble suitable parts to form a reasonable construct based on experience. In this way,redundant operations can be reduced and the time and cost required for conducting biological experiment ought to be minimized. Compared with other methods[12],the algorithm complexity of this method is O(L·D2). It doesn’t possess the advantage of speed but it can select the most suitable parts to form a bio-system referred to other successful cases,but it is better than the algorithm complexity of exhaustive algorithm which is O(DL). As described previously,this method is based on Bigram Model. It means every part involved in the assembly process is only concerned with the part prior to it. But in real world DNA assembly process,for an example,whether a gene can be expressed effectively is not only related to its RBS but also its promoter. In order to simulate real world assembly process,N-gram Model should be introduced. This model means every part involved in the assembly process is concerned with N-1 parts prior to it. But in this model the conditional probability is very difficult to calculate. When N = 3 or 4,though the accuracy in other natural language applications such as machine translation,part-of-speech tagging,intelligent input method will increase significantly,powerful computer will be needed[14]. Next step we will develop a 3-gram Model and take plasmids backbone sequence into account to facilitate the DNA assembly process in synthetic biology.
When calculating the conditional probability,we used Add-one (Laplace) smoothing to overcome zero-frequency problem. It is always not a good choice [17]. It was used for considering that any two parts compliant with the same standard can be connected and for simplicity. Due to few applications of statistical language model in synthetic biological informatics,we do not know which smoothing technology is more effective. But the weakness of Add-one (Laplace) smoothing such as giving too much of the probability space to unseen events,worst at predicting the actual probabilities of bigrams are well-known[17]. We will develop 3 or 4-gram Model and expand the corpus to simulate the assembly process more reasonably. And other smoothing technology such as Good-Turing Smoothing,Katz backoff,Interpolation Smoothing [19-20] will be considered and used to improve the mathematic model. As described previously,we downloaded a relatively sparse corpus from iGEM website. We consider expanding the corpus to widely used plasmids and count the usage of features and two or three adjacent features. In this way,the statistical language model can be used more universally and tested in synthetic biology. But the description of the nature of parts is a more difficult issue. This can be solved by the development of an ontology giving the community a common controlled vocabulary to describe genetic parts. And developing the Synthetic Biology Open Language will promote this process.
Acknowledgements Authors acknowledgethe BBF and the iGEM community for contributing the RFCs and BioBricks parts upon which this project was developed. Thanks for Prof. Peccoud and Mandy Wilson from Virginia Bioinformatics Institute guiding authors collecting the data.
| [1] |
GOLER J A, BRAMLETT B W, PECCOUD J. Genetic design: rising above the sequence[J]. Trends Biotechnology, 2008(26): 538–544.
( 0) 0)
|
| [2] |
GRASLUND S, NORDLUND P, WEIGELT J, et al. Protein production and purification[J]. Nature Methods, 2008, 5(2): 135–146.
DOI:10.1038/nmeth.f.202 ( 0) 0)
|
| [3] |
GHAEMMAGHAMI S, HUH W K, BOWER K, et al. Global analysis of protein expression in yeast[J]. Nature, 2003(425): 737–741.
( 0) 0)
|
| [4] |
CZAR M J, CAI Y, PECCOUD J. Writing DNA with GenoCAD[J]. Nucleic Acids Research, 2009, 37(suppl 2): W40–W47.
( 0) 0)
|
| [5] |
CAI Y, WILSON M L, PECCOUD J. GenoCAD for iGEM: a grammatical approach to the design of standard-compliant constructs[J]. Nucleic Acids Research, 2010, 38(8): 2637–2644.
DOI:10.1093/nar/gkq086 ( 0) 0)
|
| [6] |
ADAMES N R, WILSON M L, FANG G, et al. GenoLIB: a database of biological parts derived from a library of common plasmid features[J]. Nucleic Acids Research, 2015, 43(10): 4823–4832.
DOI:10.1093/nar/gkv272 ( 0) 0)
|
| [7] |
ISAACS F J, DWYER D J, DING C, et al. Engineered riboregulators enable posttranscriptional control of gene expression[J]. Nature Biotechnology, 2004(22): 841–847.
DOI:10.1038/nbt986 ( 0) 0)
|
| [8] |
GARDNER T S, CANTOR C R, COLLINS J J. Construction of a genetic toggle switch in Escherichia coli[J]. Nature, 2000, 403(6767): 339–342.
DOI:10.1038/35002131 ( 0) 0)
|
| [9] |
Atkinson M R, Savageau M A, Myers J T, et al. Development of genetic circuitry exhibiting toggle switch or oscillatory behavior in Escherichia coli[J]. Cell, 2003(113): 597–607.
( 0) 0)
|
| [10] |
ARKIN A. Setting the standard in synthetic biology[J]. Nature Biotechnology, 2008(26): 771–774.
( 0) 0)
|
| [11] |
CANTON B, LABNO A, ENDY D. Refinement and standardization of synthetic biological parts and devices[J]. Nature Biotechnology, 2008, 26(7): 787–793.
DOI:10.1038/nbt0708-771 ( 0) 0)
|
| [12] |
DENSMORE D, HSIAU T H C, BATTEN C, et al. Algorithms for automated DNA assembly[J]. Nucleic Acids Research, 2010, 38(8): 2607–2616.
DOI:10.1093/nar/gkq165 ( 0) 0)
|
| [13] |
COLL A, WILSON M L, GRUDEN K, et al. Rule-based design of plant expression vectors using GenoCAD[J]. PLoS ONE, 2015, 10(7): e0132502.
DOI:10.1371/journal.pone.0132502 ( 0) 0)
|
| [14] |
JELINEK F. Statistical methods for speech recognition (Language, Speech, and Communication). Cambridge,MA: MIT Press, 1998 .
( 0) 0)
|
| [15] |
PHILLIPS I E, SLIVER P A. A new biobrick assembly strategy sesigned for facile protein engineering[J/OL]. DSpace@MIT, http://dspace.mit.edu/handle/1721.1/32535,2006-04-20/2016-04-01.
( 0) 0)
|
| [16] |
CAI Y, HARTNETT B, GUSTAFSSON C, et al. A syntactic model to design and verify synthetic genetic constructs derived from standard biological parts[J]. Bioinformatics, 2007, 23(20): 2760–2767.
DOI:10.1093/bioinformatics/btm446 ( 0) 0)
|
| [17] |
CHEN S F, GOODMAN G. An empirical study of smoothing techniques for language modeling[J]. Computer Speech and Language, 1999(13): 359–394.
( 0) 0)
|
| [18] |
VITERBI A J. A personal history of the viterbi algorithm[J]. IEEE Signal Processing Magazine, 2006(23): 120–142.
( 0) 0)
|
| [19] |
HUANG F L, YU M S, HWANG C Y. An empirical study of good-turing smoothing for language models on different size corpora of chinese[J]. Journal of Computer and Communications, 2013(1): 14–19.
( 0) 0)
|
| [20] |
Katz S M. Estimation of probabilities from sparse data for the language model component of a speech recogniser[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35(3): 400–401.
DOI:10.1109/TASSP.1987.1165125 ( 0) 0)
|
 2016, Vol. 14
2016, Vol. 14

