单细胞转录组数据分析中的数学

doi: 10.12113/202307007

罗琴琴，雷锦志

天津工业大学数学科学学院，应用数学中心，天津市 300398

基金项目: 国家自然科学基金项目(No.11831015)

详细信息

通讯作者

雷锦志，男，教授，博导，研究方向：计算数学，计算系统生物学.E-mail: jzlei@tiangong.edu.cn.

中图分类号: Q522;R318.04

文献标识码: A

文章编号: 1672-5565(2025)01-001-27

Mathematics in single-cell RNA transcriptome analysis

LUO Qinqin ， LEI Jinzhi

School of Mathematical Sciences, Center for Applied Mathematics, Tiangong University, Tianjin 300398 ， China

摘要

近年来，高通量单细胞测序技术为生物学研究带来了深刻的新发现，单细胞 RNA 测序技术的快速发展使得人们能够以单个细胞的分辨率定量研究细胞全基因组的转录水平。如何从高维的单细胞 RNA 测序数据中获取关于细胞和基因组的有用信息，是单细胞 RNA 测序数据分析中备受关注的重要问题。为此，广大研究者对单细胞 RNA 测序数据分析问题进行了大量的研究，开发了许多计算方法和相应的软件包。本综述将总结单细胞 RNA 测序数据分析的常用方法及其所涉及的数学基础，主要内容包括对原始数据进行预处理、聚类分析、拷贝数变异分析和非负矩阵分解等。本文重点介绍相应数据处理方法背后的数学原理，揭示如何利用数学工具获取单细胞 RNA 测序数据的信息，以便于数学工作者进行单细胞数据分析工作和对现有方法进行深入探索与改进。

关键词

单细胞转录组测序数据 / 数据预处理 / 聚类分析 / 数学基础

Abstract

In recent years, high-throughput single-cell sequencing technology has brought profound new findings to biological research. The rapid development of single-cell RNA sequencing technology enables researchers to study the transcriptome of individual cells. How we can obtain helpful information about cells and genomes from high-dimensional single-cell RNA sequencing data is an important issue in analyzing single-cell RNA sequencing data. Many researchers have conducted studies on single-cell RNA sequencing data analysis and developed many computational methods and corresponding software packages. This review summarizes the classical computational methods and mathematical basis involved in single-cell RNA sequencing data analysis, including data preprocessing, dimensionality reduction, clustering analysis, pseudo-time analysis, copy number variation analysis, and non-negative matrix factorization. We mainly focus on the mathematical principles behind the corresponding data processing methods, reveal how we can apply mathematical tools to obtain information from single-cell RNA data, and provide guidance for mathematicians to analyze single-cell data and to further develop and improve the existing methods.

Keywords

Single-cell RNA-seq data / Data preprocessing / Clustering analysis / Mathematical basic

1 数据描述 2 数据预处理 2.1 数据质控 2.2 标准化处理 2.3 数据归一化 2.4 筛选高变基因 2.5 主成分分析数据降维 2.6 数据可视化 2.6.1 t-SNE 方法 2.6.2 UMAP 方法 2.7 数据整合 3 聚类分析 3.1 聚类分析的基础 3.1.1 样本间距离与相似度 3.1.2 类与类间距离度量 3.2 常见的聚类算法 3.2.1 k-均值聚类 3.2.2 层次聚类法 3.2.3 谱聚类 3.2.4 基于模块度的 Louvain 聚类算法 3.3 聚类分析的应用 3.3.1 细胞类型的确定 3.3.2 Doublet的去除 3.3.3 伪时间分析 4 基因拷贝数变异分析 4.1 预处理 4.2 估计二倍体细胞的拷贝数基线值 4.3 寻找染色体断点 4.4 识别克隆亚群 5 单细胞转录组数据的非负矩阵分解 5.1 矩阵分解 5.2 非负矩阵分解 5.3 单细胞转录组数据的非负矩阵分解 6 总结与展望

在过去的十多年里，高通量测序技术被广泛应用于生物和医学的各种领域，极大促进了相关领域的研究。特别是在近年来，单细胞 RNA 测序（Single-cell RNA sequencing，scRNA-seq）技术得到蓬勃发展^[1-2]，使得研究人员可以在单个细胞水平揭示全基因组范围内所有基因的转录情况。通过单细胞 RNA 测序技术，可以很好地研究细胞间的表达差异性和不同细胞亚群的数据特征^[3-5]。

对单细胞 RNA 测序数据的分析可以应用于许多问题的研究。例如，根据单细胞转录组数据分析可以识别不同类型细胞的数据特征，基于每个细胞基因表达谱数据进行细胞类型聚类和构建大规模单细胞图谱^[6-8]。还可以根据所构建的单细胞图谱研究复杂器官中不同细胞亚群的功能，了解细胞间的差异以及各种细胞群体间的协作关系。根据单细胞数据集的数据特征，可以识别细胞类型和发现稀有细胞群^[9]，同时还可以结合基因调控关系更好地理解转录动力学和细胞表型变化之间的动态演变过程^[10-11]。单细胞 RNA 测序数据可以应用于分析不同器官、组织或疾病状态下的基因差异表达，用于分析多种细胞类型的细胞命运、状态和功能，为探索胚胎发育、肿瘤演变、神经系统病变、免疫疾病发生等复杂生物学过程的动力学机制提供了更高分辨率的工具。例如，在对复杂疾病的研究中，可以通过单细胞测序数据分析探索疾病潜在的治疗靶点^[12]，发现生物标志物和进行疾病分型，发现并鉴定异常增殖的细胞类型，并结合传统病理学特征进行疾病的分型^[13]。在肿瘤学研究中，可以通过对肿瘤组织及其微环境细胞进行单细胞测序来揭示肿瘤微环境的组成^[14-15]，肿瘤细胞的耐药性变化以及肿瘤干细胞的分化，肿瘤浸润免疫细胞的异质性和免疫微环境特征^[8，16]，肿瘤细胞的动态变化关系以及各种免疫细胞在不同肿瘤免疫治疗中的潜在功能等^[3，9]。

单细胞 RNA 测序数据分析，首要任务是根据数据信息识别细胞的类型^[17]。为此，需要根据单细胞转录组数据进行聚类分析。单细胞 RNA 测序数据的聚类分析与传统数据的聚类分析原理相似，即通过计算细胞与细胞间的相似度度量，从高维的基因表达谱矩阵中学习到各个细胞之间的关系并进行聚类。目前已经有各种各样的聚类方法被开发出来，例如 SIMLR 算法^[18]，Seurat 软件包中使用的谱聚类（Spectral clustering）算法^[19]，还有基于非负矩阵分解的方法 SoptSC^[20]和 scRCMF^[21]等。有大量聚类算法是将降维方法和通用的聚类方法结合起来，例如将 t-SNE 数据降维方法与 k-均值聚类算法结合^[22]。此外，还可以通过综合性的聚类算法 SC3 将多种聚类方法所得到的结果合并起来构建共识矩阵，然后对共识矩阵进行层次聚类^[22]。目前所采用的无监督聚类算法普遍面临着一个巨大的挑战^[23]，就是如何确定细胞类型的数量。为解决这一问题，通常需要参考先验知识或通过统计方法对细胞类别的数量进行推断。

对细胞进行聚类以后，一个重要的问题就是如何识别细胞类型。通常，可以使用标记基因来鉴定细胞的类型。在生物学上，标记基因是指在不同细胞类中表达具有显著差异的基因。从数学的角度来说，通过不同算法寻找和定义差异基因的方式不一样，由此会得到不同的差异基因集合。例如在 SIMLR 方法中使用 Laplacian 分数来发现细胞亚群的差异基因^[18]，而 scRCMF 方法则通过非负矩阵分解后得到的基矩阵和系数矩阵来标记基因，即将各个类别细胞中表达量最多的基因作为标记基因^[21]。SC3 算法则是首先找到平均表达值较高的基因，然后对这些基因作配对差异检验，以此来确定这些基因是否是标记基因^[22]。许多标记基因都是在聚类完成后通过统计检验方法进行确定的。确定标记基因的方法可以与所使用的聚类方法相互独立。但也有一些算法，特别是与矩阵分解相关的算法，确定标记基因与分类是在同一步骤中完成的，例如 SoptSC^[20]和 scRCMF^[21]。

在对细胞进行聚类分析和细胞亚群识别以后，在生物学上感兴趣的问题是如何将不同的细胞投影到细胞表型变化的动态变化图谱中。对这一问题的回答可以通过伪（拟）时间分析来进行。伪时间分析，也叫做细胞的拟时序排列，将单细胞数据基于相似度投影到一维空间中，根据细胞的伪时间信息推测细胞的发育轨迹或细胞谱系^[24-25]。当前用来估计伪时间的算法主要有两种，一种是使用数据降维技术将高维的转录组数据降到低维空间中，并根据低维空间的数据点位置信息定义伪时间信息^[26-27]；另一种是通过构建以细胞为节点，以细胞间相似度为边的细胞-细胞图（Graph），然后通过计算得到细胞-细胞图的最小生成树（MST）推测伪时间轨迹^[28]。第一种方式的代表算法是 Monocle2^[27]，它首先对数据作主成分分析（PCA）或者扩散映射投影到低维空间中，然后使用 DDRTree 算法选择一组数据的质心，构造一棵生成树，再将细胞移动到它们最近的树的节点。这一算法需要用户选择一个根节点，每个细胞的伪时间就是这个细胞沿着树到达根节点的测地线距离。此外，根据降维和距离计算方法的不同，还有很多不同的算法。例如，SLICER 算法与 Monocle2 算法的思想相似，只是降维的方式不同^[26]；扩散伪时间（DPT）方法利用扩散样随机游走（Diffusion-like random walk）来测量细胞间的转移，通过比较细胞向不同命运分化的概率对细胞进行排序^[29-30]；TSCAN^[31]和 Waterfall^[32]估计伪时间的策略是相似的，都是将数据嵌入到低维空间中，然后对数据进行聚类，构建最小生成树连接各个类。第二种方法的代表算法有 Wishbone^[33]算法和 Wanderlust^[34]算法，主要通过构建细胞-细胞图，计算每个细胞与根节点细胞的距离，来推断细胞的分化关系。还有一些其它的伪时间估计工具，例如 Mpath 方法^[35]，使用基于邻域的细胞状态转换进行伪时间估计，TASIC 方法使用概率图模型进行计算^[36]。到目前为止，如何确定细胞状态之间的过渡概率仍然是具有挑战性的问题。近年来一些工作受到类似于 Waddington 景观的启发，试图通过能量景观量化描述细胞命运转变的过程，如细胞分化等。例如，SCENT^[37]和 scRCMF^[21]方法使用熵来测量细胞的当前状态，而 scEpath^[38]是一种使用统计物理建模绘制单细胞动态过程的能量景观的方法，通过这一方法获得细胞状态和重建谱系和细胞伪时序之间的过渡概率。

当前，针对单细胞测序数据的分析是生物信息学研究的热点领域，众多数据分析工具和软件包被开发出来，研究人员可以很方便地使用各种工具进行高质量的数据分析。这些工具包的广泛和便捷使用很容易带来一个弊端，就是对相关分析方法背后的数学原理的了解不够充分，不利于对结果进行科学解释和深入发展。从数学的角度来看，对单细胞测序数据的分析主要是对基因表达矩阵的数据分析，主要包括高维数据的降维、聚类、稀疏矩阵分解等，涉及大量的矩阵分析和统计学知识^[39]。本综述文章将介绍单细胞 RNA 测序数据分析的基本方法，重点介绍相关方法背后的数学基础，通过数学语言阐述单细胞 RNA 测序数据分析的实质内容，以增进对数据分析方法基本数学理论的理解。

1 数据描述

自 2009 年由汤富酬等^[1]开发出了单细胞转录组测序技术以来，目前已经有几十种不同的单细胞转录组测序技术相继被开发出来^[2]。对于不同的技术方法，主要分为两步：第一步是将细胞进行分离，获得单个细胞；第二步是对分离好的细胞进行转录组测序。不同的测序技术对这两个步骤可以分别采用不同的方式，各具特点。这里重点介绍数据分析部分，关于生物技术的详细介绍请参考相关的文献。不管采用什么样的测序技术，通过对所得到的数据进行序列比对后，会得到一个二维计数矩阵，通常以每一行表示一个基因在不同细胞中的（被观测到的）表达水平，每一列表示一个细胞不同基因的（被观测到的）表达水平，这样的计数矩阵也被称为基因表达矩阵（Gene expression matrix）（图1）。

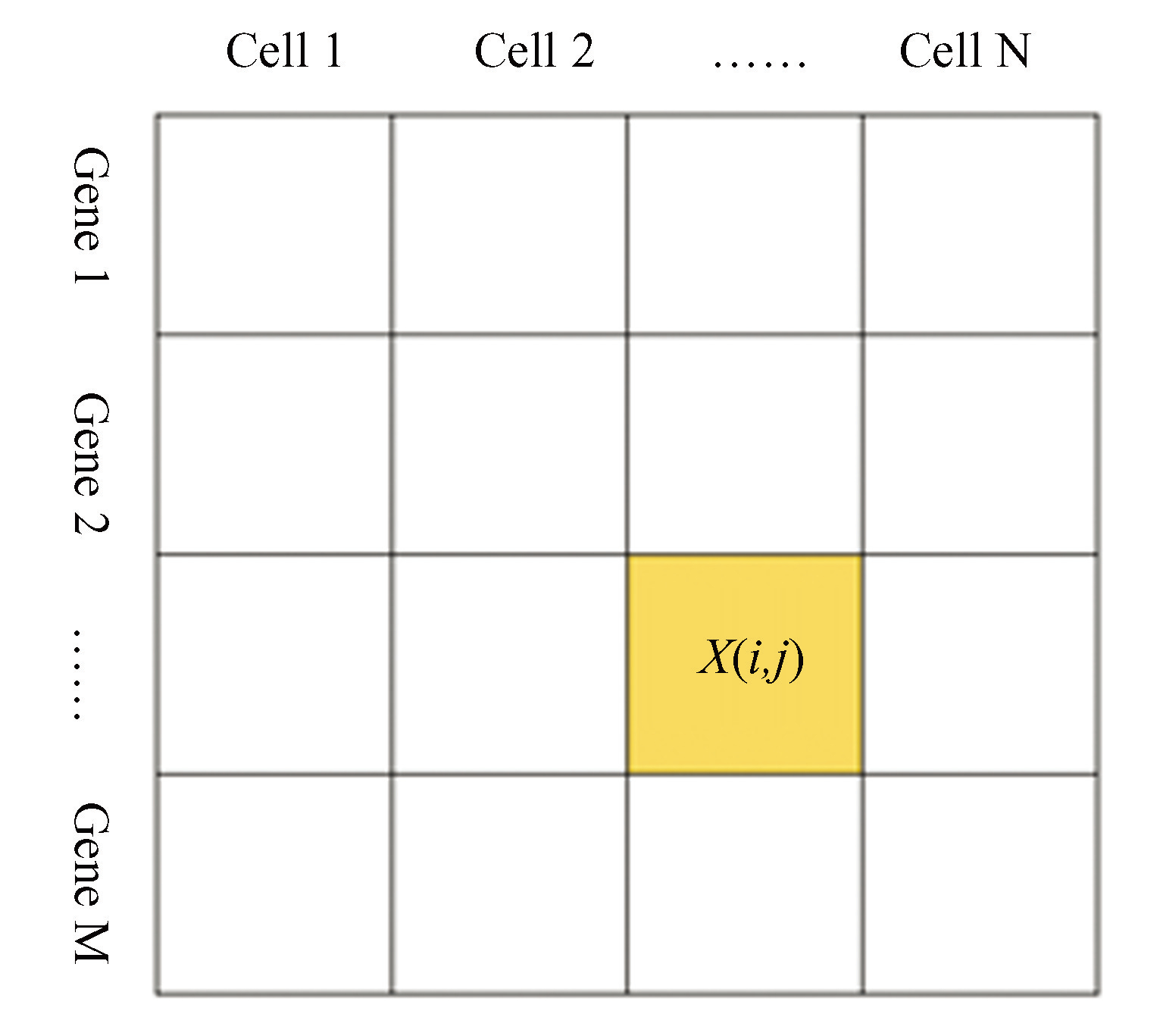
图1基因表达矩阵

Fig.1Gene expression matrix

在基因表达矩阵中，很多基因仅仅在一些细胞亚群中表达，而在其它细胞中不表达。同时，由于单细胞测序深度或实验操作过程等原因导致一些基因即使表达了，但是却未被检测到，导致基因表达矩阵中出现大量的 0 值，表现出高度的稀疏性。这种稀疏性背后隐藏着一个重要问题，即如何区分实际测量所得到的 0 值是代表相应基因的低表达或不表达，还是代表基因表达未被检测到。

基因表达矩阵

X \in R^{m \times n}

通常是高维稀疏的非负矩阵。该矩阵的行数 m 表示所测序的基因数量。以人体细胞为例，通常包括两万到三万个基因。列数 n 表示所测序的细胞数量，根据测序实验的规模不同，细胞个数可以从几百个到几十万个不等。

对于一个基因表达矩阵

X \in R^{m \times n}

，如果以每个细胞的转录组水平作为单元，则列向量

x_{j} \in R^{m}

表示第 j 个细胞的转录组水平：

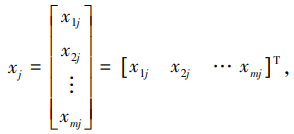
其中x_ij表示通过测序方法所得到的第 i 个基因在第 j 个细胞中的表达水平，上标 T 表示向量的转置。通过表示细胞转录组水平的向量，包含 n 个细胞的基因表达矩阵表示为

X = [x_{1}, x_{2}, \dots, x_{n}]

(1)

为叙述方便，下面列出常用的向量范数。假设有 n 维向量

x = {[x_{1}, x_{2}, \dots, x_{n}]}^{T},

定义向量的 0-范数

‖ x ‖_{0}

为 X 中非零元的元素个数，1-范数表示

‖ x ‖_{1}

中各个元素的绝对值之和，2-范数

‖ x ‖_{2}

表示 X中各个元素的平方和的开平方根，而

\infty

-范数

‖ x ‖_{\infty}

表示X 的分量中绝对值最大的取值，即

\begin{matrix} ‖ x ‖_{1} = \overset{n}{\underset{i = 1}{Σ}} |x_{i}|, ‖ x ‖_{2} = \sqrt{\overset{n}{\underset{i = 1}{Σ}} x_{i}^{2}}, \\ ‖ x ‖_{\infty} = \underset{1 ⩽ i ⩽ n}{m a x} |x_{i}| \end{matrix}

(2)

令单细胞 RNA 测序数据的基因表达矩阵X如图1所示，相应的数学表示为式（1），X中第i行第j列的元素 X（i，j）=x_ij 表示基因 i在细胞中 j的表达量。以 cell_j表示基因表达矩阵的第 j列，即第 j个细胞所包含的基因表达信息，而 gene_i表示第 i个基因在不同细胞中的表达量所构成的行向量，对应于矩阵X中的第i行。对于给定的基因表达矩阵，除了表示基因表达水平的计数外，描述数据的信息还包括数据的元信息（Metadata），例如每个细胞的编号（Barcode）和数据中每个基因的名字。有时也把基因称为是特征（Feature）。在单细胞转录组数据中，通常用nFeature表示一个细胞表达了多少种基因，即一个细胞列向量的非零元个数，而以nCount 表示一个细胞所有基因的表达量之和，即一个细胞列向量的 1-范数。以第 j个细胞cell_j=x_j为例，有

{nFeature}_{j} = {‖x_{j}‖}_{0}, {nCount}_{j} = {‖x_{j}‖}_{1}

(3)

对于同一数据集中的不同细胞，其对应的特征可以不一样。

2 数据预处理

通过测序技术所得到的原始数据（Raw data）是一个维数很高的稀疏矩阵，包含了较多的冗余信息，并不适合直接用于数据分析。因此在进行分析前首先需要对原始数据进行预处理，减少数据信息的冗余和噪音。预处理的步骤包括数据质控、标准化、归一化、高变基因的选择和降维处理等。经过预处理后的数据既能消除部分冗余信息，减少后续分析的计算量，更适合于用来探索数据背后隐藏的有用信息。数据预处理的一般流程图如图2所示。

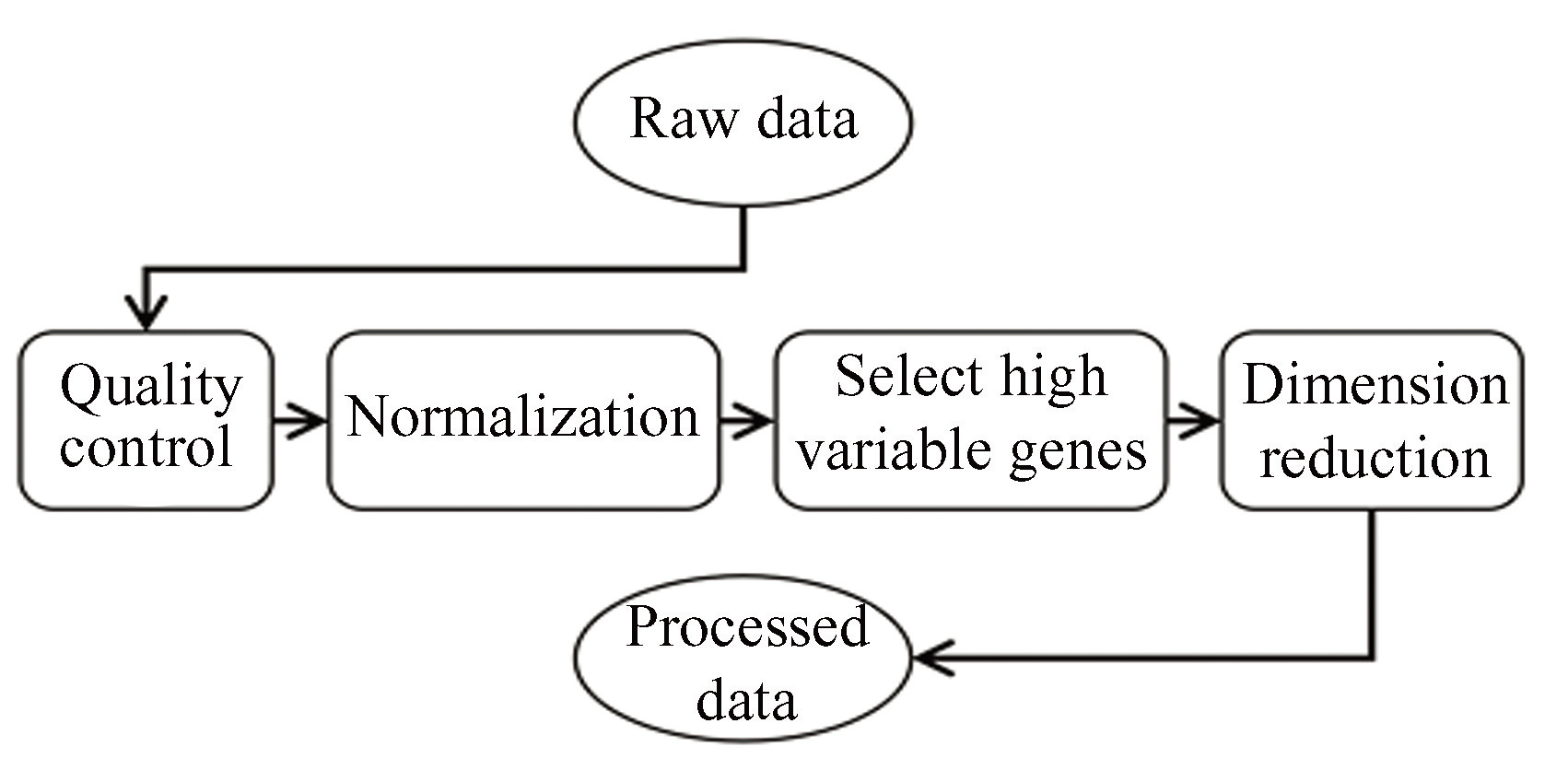
图2数据预处理

Fig.2Data preprocessing

2.1 数据质控

在对单细胞测序数据进行分析的过程中，首先需要对数据进行质量控制以排除因为测序技术所造成的异常数据。以 Genomic 10X 公司的基于液滴的 RNA 测序技术所获得的数据为例，在捕获细胞时，通常期望得到包含一个细胞和一个磁珠的液滴。但是由于技术原因，有可能会产生 dropout 和 doublet 的情况，其中 dropout 代表一个液滴里没有细胞，而 doublet 代表一个液滴里有两个或两个以上的细胞。这两种液滴都是不合格的，因此需要把这两种情况过滤掉。与之对应，在对基因表达数据进行处理时需要过滤表达基因总量nCount太大或太小的细胞。此外，对于只在少量细胞中表达的基因，也需要选择出来并过滤掉，因为这类基因包含的信息量太少，会对数据的整体分析造成干扰。除了这两项关于细胞和基因的指标原则外，同时还需要过去除线粒体基因转录本比例太大的细胞。因为正常细胞的 RNA 主要由三部分组成，分别是细胞质 RNA、核糖体 RNA 和线粒体 RNA。若某个“细胞”（液滴）的转录本分子总数低、检测到的基因数少、线粒体基因所占的比例大，就意味着这个“细胞”可能是一个已被破坏的细胞。当细胞破裂死亡时，细胞质会从细胞中流出，只有线粒体 RNA 被保留下来了并维持较高的比例。在数据处理中，需要选择一个阈值来去除线粒体基因表达较高的细胞^[40]。通常，来自不同组织的单个细胞中线粒体基因的平均表达水平是不一样的，这个阈值的选择需要根据具体情况设定，不能一刀切。需要注意的是，上述三个质控指标需要联合考虑，单独考虑这些指标可能会造成细胞状态判断的失误。例如，线粒体基因占比相对较高的细胞也可能是代谢过程比较积极的细胞，例如心脏细胞（线粒体基因占总 mRNA 的 30%）^[41]或者肿瘤细胞。在设置阈值时，尽可能将阈值设置宽松些，避免无意间滤除有效的细胞群。

下面以 Genomic 10X 公司提供的人体外周血数据集（Pbmc3k）为例进行说明（数据下载链接为https://cf.10xgenomics.com/samples/cell/pbmc3k/pbmc3k_filtered_gene_bc_matrices.tar.gz）。该数据集共包括 2 700 个细胞，32 783 个基因。在本文的算例中如不特别指出，均指以该数据集为例。

原始数据的分布如图3（a）所示。从图3（a）可以看到，该数据集中大部分细胞所表达的基因数少于2 500 个。因此，可以设置过滤条件将质量不好的细胞过滤掉，即只保留所表达基因的数量满足

200 ⩽ {nFeature}_{j} ⩽ 2500

的细胞。图3（a）给出各个细胞的基因表达总量的分布。可以看到有少量细胞具有异常高（＞10 000）的基因表达总量。为了过滤掉由于技术原因导致的 dropout 或 doublet，根据总体的基因表达数据对基因表达的总量设置阈值

1000 ⩽ {nCount}_{j} ⩽ 10000

进行限制。在数据筛选中，通常只选择线粒体基因的 RNA 总量所占比例不超过一定阈值的细胞（通常可以取为 10%）。因此，设置

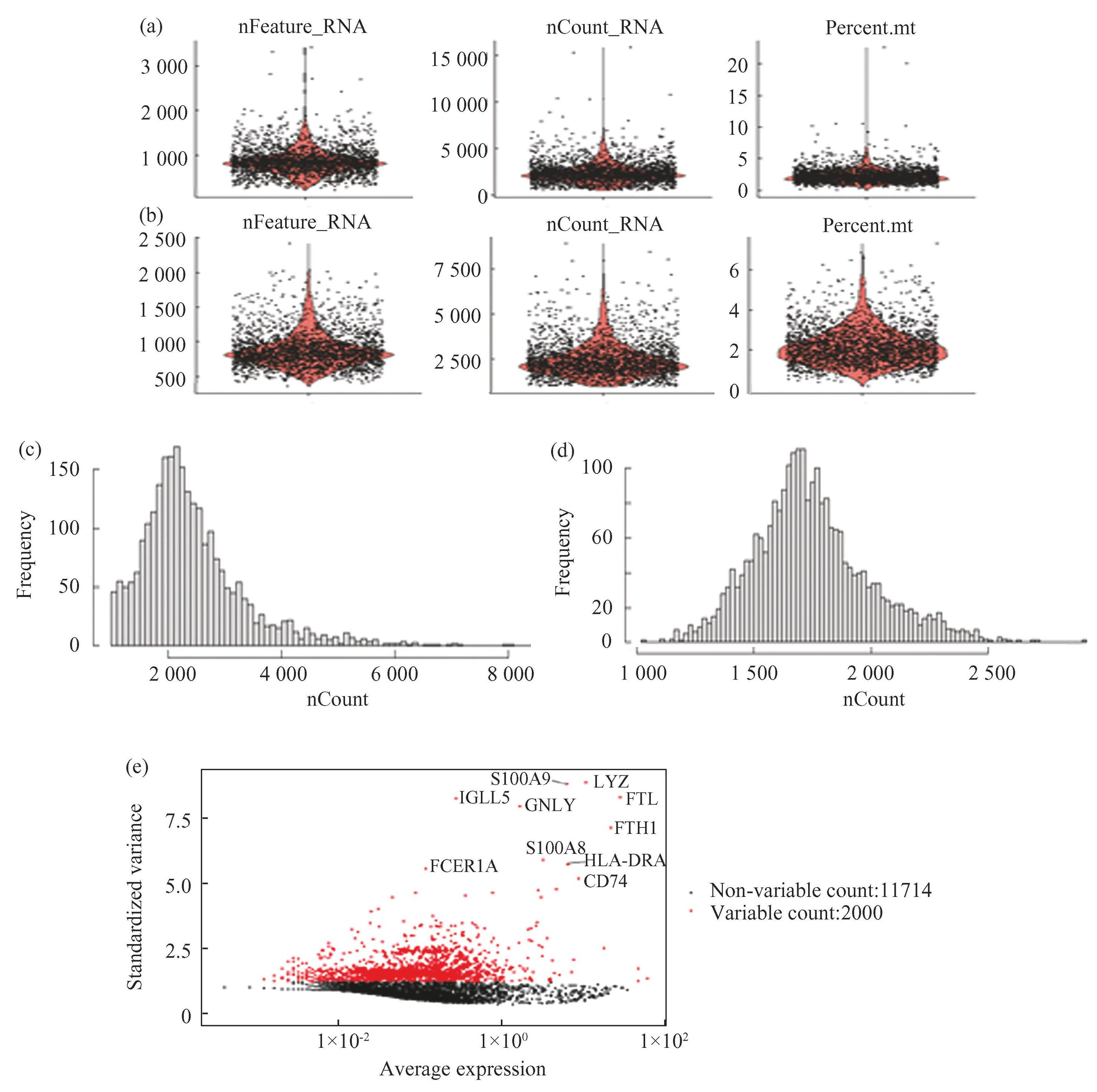
图3单细胞数据集的特征

Fig.3scRNA-seq dataset's feature

注：（a）过滤前单细胞 RNA 数据集的特征；（b）过滤后数据集的特征；（c）归一化前总基因表达值的分布；（d）归一化后总基因表达值的分布；（e）高变基因.（扫本文首页二维码见彩图）。

{percent .}^{} {m t}_{j} ⩽ 10

其中percent.mt_j表示第j个细胞中线粒体相关基因表达量的总和与细胞总表达量的比值的百分数。此外，还需要对基因进行筛选，选择在大于给定阈值数量的细胞上表达的基因进行分析，即限制

‖ {gene}_{i} ‖_{0} ⩾ min . cells,

其中 min.cells表示基因所表达细胞数量的阈值。因此，对于一个包含 n个细胞，m个基因的基因表达矩阵，上述数据过滤的条件用数学语言描述就是：

\{\begin{matrix} 200 ⩽ n {Feature}_{j} ⩽ 2500, j = 1,2, \dots, n, \\ {percent . mt}_{j} ⩽ 10, j = 1,2, \dots, n, \\ 1000 ⩽ n {Count}_{j} ⩽ 10000, j = 1,2, \dots, n, \\ ‖ {gene}_{i} ‖_{0} ⩾ m i n . c e l l s, i = 1,2, \dots, m . \end{matrix}

(4)

经质控处理后的数据可以利用数据的小提琴图进行展示。图3（b）给出了上述数据在质控筛选后每个细胞表达基因的个数、总的基因表达量和线粒体基因所占基因表达总量百分比的情况。小提琴图中的黑色点表示数据点的读数，红色区域的宽度表示相应数据值（对应于纵坐标）的频率。这里需要注意的是许多软件包的小提琴图中所给出的频率值是经过光滑化处理以后所拟合出来的曲线值，而不是直接通过数据计算所得到的频率值。通过这里的小提琴图展示可以看到经过过滤后的数据消除了离群点，在一定程度上提升了数据的质量。

2.2 标准化处理

对数据进行质控筛选以后，通常需要进行数据标准化处理。这里先介绍数据标准化处理的相关名词。以n维列向量X为例，数据的中心化也叫做零均值化（Zero-centered），即对数据做以下变换：

x^{'} = x - m e a n (x), m e a n (x) = \frac{1}{n} \overset{n}{\underset{i = 1}{Σ}} x_{i}

(5)

这里mean（x）表示向量X中各分量的平均值。

数据的标准化（Standardization）是对中心化的进一步处理，常用的标准化方法有 Z-score 标准化，即下面的变换：

x^{'} = \frac{x - m e a n (x)}{s d (x)}, s d (x) = \sqrt{\frac{1}{n} \overset{n}{\underset{i = 1}{Σ}} {(x_{i} - m e a n (x))}^{2}}

(6)

这里sd（x）表示向量X中各分量的标准差。在数据分析中，通常假设经过 Z-score 标准化处理后的分量数据近似满足标准正态分布。这一假设是需要注意的，如果一些数据不满足这一假设，则需要根据其实际分布对数据分析方法进行修正。

在数据的分类和聚类等算法中，经常通过距离来度量不同样本之间的相似性，或者采用主成分分析（PCA）方法进行数据降维。对物理量进行度量的数值通常与量纲有关。通过Z-score处理以后的标准化数据是无量纲的，可以消除不同量纲的影响。但是也需要注意到，在进行Z-score标准化处理时，因为不同细胞数据所对应的均值和方差不同，因此对不同细胞数据的标准化处理公式中的变化参数 mean（x）和sd（x）是不一样的，这样的标准化处理会造成细胞间数据差异性的丢失。例如，不同细胞的数据经过标准化处理以后的数据均值和方差都是相同的。

2.3 数据归一化

数据的归一化（Normalization）是一种将数据映射到区间[-1，1]或者[0，1]的处理方法。一种常见的归一化方法是 Min-Max 归一化方法，该方法将数据映射到区间[0，1]，对应的计算公式为

x^{'} = \frac{x - m i n (x)}{m a x (x) - m i n (x)}

(7)

这里 min（x）和max（x）分别表示细胞向量 X的最小值和最大值。需要注意的是每个细胞的最小值和最大值不同，因此上面的归一化方法对不同细胞的变化尺度是不一样的，在对细胞进行差异性分析时会造成数据的扭曲。为了消除这一影响，可以采用全局性MIN-MAX归一化的方法，即对数据集

X \in R^{m \times n}

，令

x^{'} = \frac{x - M I N}{(M A X - M I N)}

(8)

其中MIN和MAX 分别为全局最小值和全局最大值，定义为

M I N = \underset{1 ⩽ j ⩽ n}{m i n} m i n x_{j}, M A X = \underset{1 ⩽ j ⩽ n}{m a x} m a x x_{j}

细胞中不同基因表达水平可以相差很大。对同一个细胞来说，有一些基因的表达值很大而有一些基因的表达值很小，因此细胞的基因表达数据的分布通常比较离散。为了减小数据的离散程度，通常对数据进行对数转换，转换后的数据方差更小，数据更加集中。可以利用数据的对数变换对每个细胞的数据做“归一化”处理，使得不同细胞之间的数据具有可比性。这里的“归一化”与一般的归一化方式不同，首先把数据映射到区间[0，1]；然后，为了放大或缩小数据间的差距，再对数据进行缩放（常选择放大数据）；最后，为了减小放大后数据的方差，再对放大后的数据作对数变换。也就是将正常归一化的数据乘以缩放因子后再做对数转换。以单个细胞的基因表达数据 X为例，对数变化的计算公式为

\begin{matrix} x^{'} = {l o g}_{a} (1 + scalefactor \times (\frac{x}{s u m (x)})), \\ s u m (x) = \overset{n}{\underset{i = 1}{Σ}} x_{i} \end{matrix}

(9)

这里 a 为对数变换的底，一般取自然对数 e 或 2，scalefactor 称为缩放因子，它可以根据数据集的规模来确定，例如可以取 scalefactor=10 000。标准化后的总基因表达量呈正态分布。图3（c）~（d）给出了标准化前后各细胞基因表达总量的分布。

除了上面的标准化处理方式以外，还有其他的处理方式，例如 DESeq^[42]，bayNorm^[43]标准化方法等。需要指出的是，数据的标准化处理方法并非一成不变，需要根据具体的问题和需要选择合适的标准化方法进行数据处理。

2.4 筛选高变基因

高变基因是指在不同细胞类中表达量具有显著差异的基因。高变基因在不同细胞之间的表达差异可以对识别细胞的特性提供重要信息。相反，如果某个基因在不同细胞中的表达水平差异很小或者是没有差异，那么该基因的表达水平对分析细胞间差异没有贡献。筛选高变基因，一方面把能够反映细胞间差异的重要信息筛选出来，另一方面能够降低数据的维度以便于下游分析。

通常可以采用基因表达水平的变异系数 cv（Coefficient of variation）来挑选高变基因。每一个基因的变异系数定义为该基因在不同细胞中表达水平的标准差与均值的比。以基因 i 为例，设y_i是由基因 i 在各个细胞中表达值（已经过预处理后的）构成的 m 维向量，则基因 i 的变异系数 cv_i 为

c v_{i} = \frac{s d (y_{i})}{m e a n (y_{i})}

(10)

其中sd（y_i）表示向量y_i各个分量的标准差，mean（y_i）表示向量y_i各个分量的均值。对每一个基因计算出变异系数后，将变异系数从大到小排列，筛选变异系数大的基因作为高变基因进行下游分析。通过这一方法可以过滤掉变异系数小，也就是包含信息较少的基因。

除了使用变异系数外，还可以使用每个基因在不同细胞中表达量的标准差来衡量该基因是否为高变基因。通常，通过高变基因的选择可以在一定程度上降低数据的维度。图3（e）给出数据集中每个基因的表达均值与标准差的散点图，并标记出前 10 个高变基因。这里通过变异系数进行高变基因选择，红色表示高变基因，黑色表示非高变基因，图中标出了前 10 个高变基因的名称。

2.5 主成分分析数据降维

在单细胞 RNA 测序数据中，每个细胞的数据包含所有基因的表达水平，通常是高维的数据，不便于后续数据分析。因此，在进行进一步的数据分析以前需要进行数据降维，以简化下游分析的计算和提取关键的特征信息。在基因表达矩阵中，每个基因的表达都可以在一定程度上体现细胞之间的差异。一些基因之间存在协同或拮抗的调控关系，在数据上表现出它们在不同细胞的表达水平具有相关性，导致数据信息的冗余。数据降维的首要目标是消除这种数据冗余，以提取低维的并且可以表示数据特征的基本信息。

主成分分析（Principal component analysis，PCA）是常用的线性化数据降维方法。主成分分析方法对含有多个变量的数据集，通过对数据特征的线性变换构建一组线性无关的新变量，使得新变量之间相互独立，并且由少数的主要变量就可以表示原数据集中不同数据差异的主要信息。

通过主成分分析所得到的主成分是指对原始变量进行线性组合以后所得到的一组新变量。在主成分分析中“主”的意思是主要的，即新变量的个数（主成分的个数）远远少于原始变量的个数，并且能够最大程度地表示原始数据的信息。主成分变量之间彼此正交，这样就保证了新的变量没有包含冗余信息。在数据的高维空间中，主成分分析可以理解为把原始数据投影到新的坐标系中，其中第一主成分为第一坐标轴，第二主成分就为第二坐标轴，以此类推。图4给出了对两维的数据经过投影到新的坐标系以后的形式，其中第一主成分给出了数据的最大差异性。

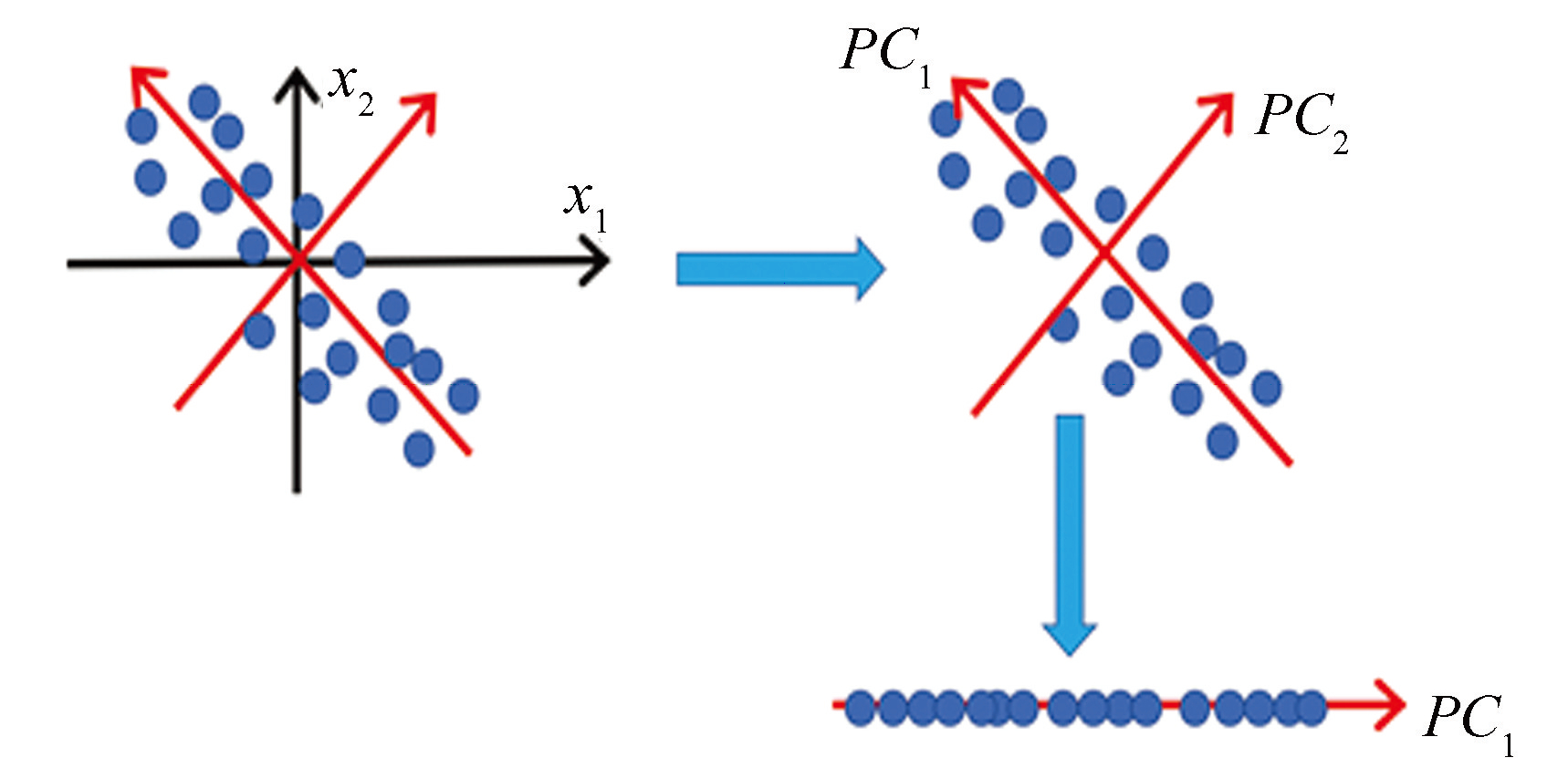
图4主成分分析（PCA）示意图

Fig.4Schematic diagram of PCA

对数据进行正交投影的方式有很多。在主成分分析中，为了最大程度地保留原始数据的解释，采用最大方差理论进行正交投影，即要求经过投影（原始数据的线性组合）以后，新的变量能够表示出原始数据的最大偏差，相应的新变量即为原数据的主成分。按照新变量的每个维度的偏差从大到小排序，分别称为第一主成分、第二主成分等。通常，选择主成分的数量需要对数据差异的解释达到 80%~90%，才能够在较大程度上解释原始数据包含的信息^[43]。

下面给出主成分分析的数学表示。假设有基因表达数据集

X \in R^{m \times n}

，共有 m 个样本（细胞），每个样本包含 n 个变量（基因）。为了便于数学表达，首先对表达矩阵取转置

Y = X^{T} = [y_{1}, \dots, y_{n}],

这里

y_{i} \in R^{m}

表示基因 i 在 m 个不同细胞中的表达水平所组成的向量，即基因 i 的表达向量。主成分分析的主要目的是寻找基因表达向量之间的线性组合，使得新的变量中分量的方差最大，即求

z = v_{1} y_{1} + v_{2} y_{2} + \dots + v_{n} y_{n}

使得 z的分量之间的方差最大。记

\bar{z} = m e a n （ z ） ， {\bar{y}}_{j} = m e a n (y_{j})

，则

\bar{z} = v_{1} {\bar{y}}_{1} + v_{2} {\bar{y}}_{2} + \dots + v_{n} {\bar{y}}_{n},

并且z 的方差为

\begin{matrix} σ^{2} = s d (z)^{2} = \frac{1}{m} \overset{m}{\underset{j = 1}{Σ}} {(z_{j} - \bar{z})}^{2} \\ = \frac{1}{m} (z - \bar{z})^{2} \\ = \frac{1}{m} {(\overset{n}{\underset{j = 1}{Σ}} v_{j} (y_{j} - {\bar{y}}_{j}))}^{2} \\ = \frac{1}{m} \underset{1 ⩽ j, k ⩽ n}{Σ} v_{j} v_{k} (y_{j} - {\bar{y}}_{j}, y_{k} - {\bar{y}}_{k}) \end{matrix}

因此，令 C 为 Y 的列向量的协方差矩阵，即

C = (C_{j k}) \in R^{n \times n}, C_{j k} = \frac{1}{m} (y_{j} - {\bar{y}}_{j}, y_{k} - {\bar{y}}_{k}),

则有

\begin{matrix} σ^{2} = \underset{1 ⩽ j, k ⩽ n}{Σ} v_{j} C_{j k} v_{k} = v^{T} C v, \\ v = {[v_{1}, v_{2}, \dots, v_{n}]}^{T} \end{matrix}

(11)

由公式（11）可以看到σ²是系数（v₁，···，v_n）的二次函数。根据主成分的含义，求解主成分的目标是在 ‖v‖=1 的条件下使σ²达到最大值，即求解优化问题

v = a r g \underset{v \in R^{n}, ‖ v ‖ = 1}{m a x} v^{T} C v

(12)

下面采用拉格朗日乘子法求解问题（12），令 f（v，λ）=v^TCv-λ（v^Tv-1），则 v和 λ 满足

\begin{matrix} \frac{\partial f}{\partial v} = 2 C v - 2 λ v = 0 \\ \frac{\partial f}{\partial λ} = v^{T} v - 1 = 0 \end{matrix}

也就是求解矩阵 C的归一化的特征值问题

C v = λ v, ‖ v ‖ = 1

此时，对应的方差为

σ^{2} = v^{T} C v = λ

上面分析表明， Y 的协方差矩阵 C 的特征值给出了相应的向量 z 的方差，即相应变量的贡献率。这里注意到矩阵 C是对称正定矩阵，其特征值都是大于零的实数。

根据上面推导过程，为求解主成分，只需要计算协方差矩阵 C 的特征值和特征向量。然后按特征值从大到小排列为 λ₁，λ₂，···，λ_n，并令相应的特征向量为v₁，v₂，···，v_n，则第i个主成分为

z_{i} = Y v_{i}

对应的贡献度为 λ_i。由上面的计算过程，前 k 个主成分的累计贡献度值为

c o n t r i b u t i o n (k) = \frac{\overset{k}{\underset{i = 1}{Σ}} λ_{i}}{\overset{n}{\underset{i = 1}{Σ}} λ_{i}}

为简单记，令特征矩阵

P = [v_{1}, v_{2}, \dots, v_{n}]

则通过主成分变换以后的数据矩阵变为

Z = Y P

前k个主成分所组成的向量对应于矩阵 Z的前k列向量，对应于每个细胞的特征以k个值来表示。

例如，对pbmc3k数据集进行主成分分析，以第一、二两个主成分表示的数据结果如图5所示。这里需要注意的是，为了减少不同基因的表达水平差异带来的影响，在进行主成分分析以前需要进行标准化处理，即对于一个基因在不同细胞中的表达水平作Z-score标准化处理。经标准化处理之后的数据再用来进行主成分分析。

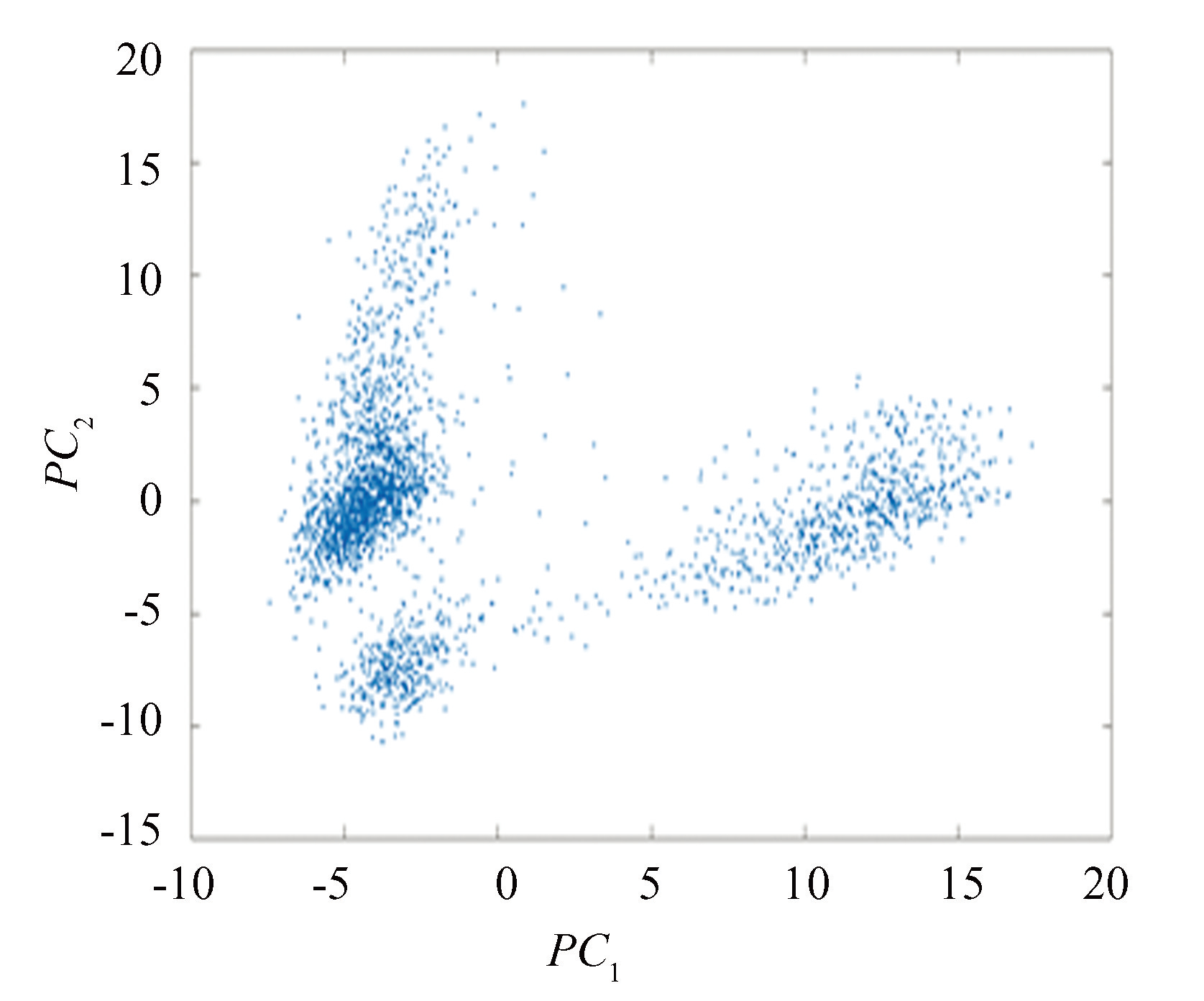
图5数据集 pbmc3k 两个主成分的投影

Fig.5Principal components projection of the dataset pbmc3k

在对单细胞测序数据的主成分分析中，注意到 Y=X^T，而 P 是正交矩阵，即P^-1=P^T。因此，由

Z = Y P = X^{T} P

可以得到

X = P Z^{T}

如果取前 k 个主成分，令

\begin{matrix} P_{1} = [v_{1} ， \dots ， v_{k}] ， P_{2} = [v_{k + 1} ， \dots ， v_{n}] ， 和 \\ Z = [Z_{1} ， Z_{2}] ， \end{matrix}

其中Z₁为 Z 的前 k 列（即 Y 的前 k 个主成分）所组成的矩阵，则有

X \approx P_{1} Z_{1}^{T}

这给出了从矩阵分解的角度对主成分分析方法的理解。

2.6 数据可视化

尽管主成分分析可以大大降低数据的维度，但是新变量的维数仍然会比较大（大于 3 维），不便于对数据进行直接可视化。为了进行高维数据的可视化，增进对数据的了解，学者提出两种可视化降维方法 t-SNE（t-distributed stochastic neighbor embedding）^[44]和 UMAP（Uniform manifold approximation and projection）^[45]。这两种算法的基本思路相似，主要是构造从高维数据空间到低维可视化空间的映射，使得在高维空间中比较相似的点在低维空间中也是比较靠近的，这样可以通过数据的低维表示把原始数据在高维空间中的特征表现出来。

数据可视化的主要思路是构建非线性映射把原始的高维数据（n 维）映射到低维空间（d 维），使得高维数据中相似的点在低维数据中也是比较靠近的。考虑两个数据空间

Ω = (R^{N} ， p)

和

ω = (R^{d} ， q ）

，其中

N ≫ d

，和对应的相似度

p : R^{N} \times R^{N} \mapsto R, q : R^{d} \times R^{d} \mapsto R .

给定高维空间 Ω 上的 m 个数据点

X = {\{x_{i}\}}_{i = 1}^{m}

，数据可视化的主要目的是希望找到低维空间 ω 中对应的 m 个点

Y = {\{y_{i}\}}_{i = 1}^{m}

与之对应，满足

p_{i j} = q_{i j}, p_{i j} = p (x_{i}, x_{j}), q_{i j} = q (y_{i}, y_{j}), \forall i, j .

然而，通常很难找到严格满足上述条件的映射。为此，可以把目标调整为找到映射使得在高维空间中样本点之间相似度p_ij的分布 P 与在低维空间中样本点的相似度q_ij 的分布Q之间的距离达到最小，也就是

\underset{Y}{m i n} D (P, Q),

上面给出了数据可视化的基本思想。不同方法的主要区别在于对相似度函数和距离D（P，Q）的不同定义。下面分别介绍 t-SNE 和 UMAP 这两种方法的基本原理。

2.6.1 t-SNE 方法

t-SNE 方法来源于 SNE 方法。在普通的 SNE 方法中，对于高维空间的两个点x_i和x_j，以 x_i为中心构建方差为σ_i的高斯分布，以x_j在x_i的邻域中的概率表示相似度，定义为

p_{j | i} = \frac{\exp (- {‖x_{j} - x_{i}‖}^{2} / (2 σ_{i}^{2}))}{\underset{k \neq i}{Σ} e x p (- {‖x_{i} - x_{k}‖}^{2} / (2 σ_{i}^{2}))},

这样，若 x_j与x_i距离越近，则相似度p_j_|_i越大。这里并不关心每个点到自己的相似度，所以设 p_i_|_i=0。而在低维空间，类似地定义 y_j在y_i的邻域中的概率 q_j_|_i为

q_{j ∣ i} = \frac{\exp (- {‖y_{j} - y_{i}‖}^{2})}{\underset{k \neq i}{Σ} e x p (- {‖y_{k} - y_{i}‖}^{2})},

即在这里统一设置

σ_{i} = 1 / \sqrt{2}

。同样，令 q_i_|_i=0。采用 KL 散度（Kullback-Leibler divergence）度量分布之间的距离，即

D (P, Q) = K L (P ‖ Q) = \underset{i \neq j}{Σ} p_{j ∣ i} l o g \frac{p_{j | i}}{q_{j ∣ i}},

通过最小化距离分布 P 和 Q 的 KL 散度来构造从原始数据空间到低维空间的映射，即可以将高维空间的数据近似映射到低维空间中。

在上面的相似度定义中，参数 σ_i 的选择是比较重要的。为此，对每个数据点 x_i定义一个困惑度（Preplexity）

{preplexity}_{i} = 2^{H_{i}}, H_{i} = - \underset{j}{Σ} p_{j ∣ i} {l o g}_{2} p_{j ∣ i}

(13)

作为约束来确定样本 x_i 的最优参数 σ_i 的取值。这里H_i 表示数据点x_i的熵。困惑度设置越大，数据分布越紧凑，通过设置困惑度参数可以调整可视化的效果。

注意到 SNE 方法中的相似度p_j_|_i是不对称的，概率p_j_|_i不等于p_i_|_j。为给出对称的 SNE 方法，可以用联合概率 p_ij 代替p_j_|_i。在高维空间中，联合概率定义为

p_{i j} = \frac{\exp (- ‖x_{i} - x_{j}‖ / (2 σ^{2}))}{\underset{k \neq l}{Σ} e x p (- ‖x_{k} - x_{l}‖ / (2 σ^{2}))},

而在低维空间中定义联合概率为

q_{i j} = \frac{\exp (- {‖y_{i} - y_{j}‖}^{2})}{\underset{k \neq l}{Σ} e x p (- {‖y_{k} - y_{l}‖}^{2})}

然而，按照上面定义的高维空间联合概率会带来异常值问题。例如，假设 x_i是一个噪声点，那么||x_i-x_j||的平方会很大，导致对所有的 j，p_ij 都会很小，因此在低维空间中 y_i对整个目标函数的影响也很小。为消除该异常值问题，可以对高维空间中的联合概率修正为

p_{i j} = \frac{p_{i | j} + p_{j | i}}{2} .

对称 SNE 方法虽然可以在一定程度上改善了 SNE 方法，但是还存在低维空间中的数据拥挤问题，也就是说在高维空间中相似度比较大的点在低维空间中过分集中。为了改善数据拥挤的问题，需要在低维空间中采用更加偏重长尾分布的方式来表示数据的相似性。为此，发展出了 t-SNE 方法，即在低维空间中采用 t-分布定义数据点的相似性

q_{i j} = \frac{{(1 + ‖y_{j} - y_{i}‖)}^{- 1}}{\underset{k \neq l}{Σ} {(1 + ‖y_{k} - y_{l}‖)}^{- 1}} .

然后，和原始SNE方法一样，采用 KL 散度定义目标函数进行优化求解。

2.6.2 UMAP 方法

UMAP 方法由 Leland McInnes 在 2018 年的 SciPy 大会上提出^[45]，其基本思想与上面的 t-SNE 的类似，只是相似度函数和分布之间距离的定义不同。

首先可以通过度量 d（x_i，x_j）来定义相似度，并且对于相似度不需要进行归一化。例如，定义点x_j在x_i的邻域内的相似度为

p_{j | i} = e^{- \frac{d (x_{i}, x_{j}) - ρ_{i}}{σ_{i}}}

(14)

其中ρ_i 是一个重要指标，代表数据点 x_i到第一个最近邻点的距离。这里的度量可以是任意的度量，而不限于欧式距离。通过参数 ρ_i的引进保证了流形的局部连续性，也就是说为每个数据点提供了一个局部的自适应指数。UMAP 把上面的非对称相似度进一步修正为对称相似度

p_{i j} = p_{i ∣ j} + p_{j ∣ i} - p_{i ∣ j} p_{j ∣ i} .

对于困惑度，UMAP 方法也采用不同于 t-SNE 的定义，即定义为

{preplexity}_{i} = 2 \underset{j}{Σ} p_{i j}

在低维空间中，UMAP 采用曲线族 1/（1+ay²^b）来定义相似度，即

q_{i j} = {(1 + a {(y_{i} - y_{j})}^{2 b})}^{- 1}

在 UMAP 中默认的超参数值为 a≈1.93，b≈0.79，其几何意义对应于对给定的超参数 min_dist=0.001，并从带有超参数 min_dist的以下分段函数中反解出参数a和b：

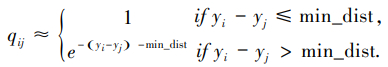
在这里，超参数 min_dist的含义表示低维空间中点之间的最小距离。这个参数控制了UMAP将数据点紧密地聚集在一起的程度，该数值越小，则嵌入的点就越紧密。随着min_dist参数的增加，UMAP倾向于 “分散”投影点，导致数据的聚类减少，对全局结构的重视程度降低。

最后，在 UMAP 中采用二元交叉熵（CE）作为目标函数，定义为

\begin{matrix} D (P, Q) = C E (P, Q) = \\ \underset{i}{Σ} \underset{j}{Σ} [p_{i j} l o g \frac{p_{i j}}{q_{i j}} + (1 - p_{i j}) l o g \frac{1 - p_{i j}}{1 - q_{i j}}] \end{matrix}

(15)

这样，通过目标函数和困惑度约束求解参数 ρ_i，σ_i 和数据点在低维空间的目标位置

Y = {\{y_{i}\}}_{i = 1}^{m}

，就可以得到原始高维数据的低维表示。

上面介绍了 t-SNE和 UMAP 的基本思路。图6给出了分别采用主成分分析，UMAP，t-SNE 三种方法对数据集 pbmc3k 进行可视化的效果。

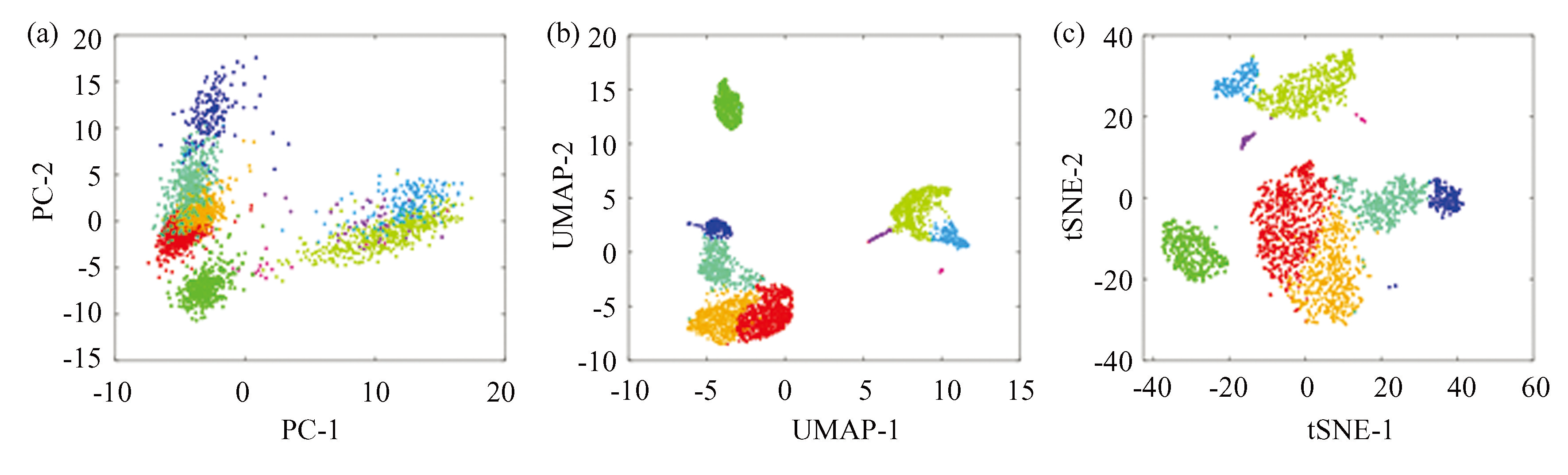
图6数据集 pbmc3k 的数据可视化

Fig.6Visualization of pbmc3k dataset

注：（a）主成分分析;（b）UMAP;（c）t-SNE.

t-SNE 和 UMAP 这两种方法具有不同的优缺点。通常来说，t-SNE 方法倾向于保持局部特征，对全局特征的保持不是很好。而 UMAP 方法对全局的结构，特别是不同亚群之间的结构可以更好地保持。UMAP 倾向于支持具有连通性的数据而t-SNE倾向于投影较离散的数据。同时，我们也注意到，这两种方法都仅仅是数据可视化方法，并不能作为降维方法来使用，由此得到的低维表示并不像 PCA 的主成分或者非负矩阵分解的因子那样具有可解释性。它们都需要用户自定义超参数，而可视化结果对参数是很敏感的。此外，这两种方法都没有唯一的最优解，通过不同的初始条件可以得到不同的解，在应用时可以通过调整参数和初始条件得到自己认为是满意的解。这里所定义的相似度本身是没有意义的，仅仅表示概率分布，可视化结果只是一个参考，最后所得到的可视化结果并不具有生物学意义。此外，数据的可视化投影并没有保留细胞与细胞间的距离，所以直接采用低维嵌入的结果进行下游的聚类分析或拟时序分析时，对结果的解释需要结合实际的生物学含义进行^[17]。

2.7 数据整合

单细胞转录组测序数据正在呈现指数级增长。随着越来越多的 scRNA-seq 数据的产生，整合不同来源（包括但不限于：不同的测序方法、样本、测序时间、实验室等）的scRNA-seq数据变得越来越重要，数据整合成为一个亟待解决的核心挑战。具体而言，如何将同一组细胞类型基于不同技术平台或由不同批次实验产生的测序数据进行修正与合并？目前已有很多研究对这一问题提出了不同的解决方法，例如，纽约基因中心的Rahul Satija课题组提出的典型关联分析方法（Canonical correlation analysis，CCA）^[46]和英国剑桥大学的John Marioni课题组提出的互近邻（Mutual nearest neighbor，MNN）^[47]方法。

典型关联分析（CCA）被广泛应用在图像分析、信号处理和基因组学等领域，是一类经典的统计学技术。它基于凸优化和特征值分解方法，搜索高维度特征的线性组合，使两组或多组数据间具有最大的整体相关性，从而实现数据降维和数据内涵结构的准确捕捉。研究人员使用CCA来进行数据整合的主要原理是假设具有同样细胞类型的两个独立的单细胞 RNA 测序数据集在本质上可视作对同一（批）转录组的两次抽样，因而具有较高的数据整体相关性。对其进行CCA分析不仅使两组数据矩阵从对应于全基因组数千个基因的高维度数据被压缩至对应于前二十项典型关联组分的低维度；更重要的是，这一线性映射还使得去除了批次效应之后的对应于细胞状态的生物学特征信息得以特异性地保留。

互近邻（MNN）搜索方法在近邻（Nearest neighbor，NN）使用余弦距离（Cosine distance）来度量两组独立单细胞测序数据集中的细胞之间的距离。首先通过计算找出两个数据集中距离最近的所有数据点对；然后，假设这些具有互相近邻对应关系的单细胞之间的表达谱差异仅由批次效应造成，从而利用其平均差异计算出批次效应量；最后，将其中一个数据集中减去该批次效应量，即得到修正后的可直接整合和对比的两组数据集。

整合后的大规模数据常常蕴含着单个数据集难以挖掘出的信息，如何对数据有效地整合，仍然是一个值得研究者们关注的重要问题。

3 聚类分析

对单细胞转录组数据进行分析的一个重要任务是识别每个细胞对应的细胞类型。为此，在单细胞测序数据分析中，需要通过聚类算法根据细胞基因表达谱的相似性将所有细胞分为不同的细胞类，然后根据每一类细胞的标志表达基因确定相应的细胞类型。通过数据聚类所得到的细胞类可以是已知确定类型的细胞，也可以是暂时无法确定的新的细胞类型或处于中间类型的过渡状态细胞。

已有许多不同的聚类算法，这些算法的基本思路各不相同。例如 Seurat 软件包使用谱聚类（Spectral clustering）算法^[19]，主要是基于共享最近邻图（SNN）和模块化优化的聚类算法来识别细胞簇。该方法首先利用主成分分析方法进行数据降维，减少原始数据中的冗余信息，将高维数据投影到低维空间中，然后计算 k-最近邻（K-nearest neighbors）细胞并构造最近邻图，通过优化模块化功能来确定具体的簇类。与 Seurat 算法类似，SIMLR 算法的关键思路也是谱聚类，但所采用的细胞间距离的度量方式与 Seurat 算法的度量不同。SIMLR 算法将数据与多个核函数进行拟合，学习合适的细胞-细胞距离度量，并通过该度量构建细胞-细胞相似性矩阵并用于聚类计算^[18]。除上述方法以外，还可以采用非负矩阵分解的方法进行细胞聚类和类型识别。例如在 SoptSC 算法中从单细胞转录组数据中学习细胞间的相似度矩阵，然后对相似度矩阵进行非负矩阵分解以获得细胞的分类^[20]。 scRCMF 算法^[21]则根据转录组数据的非负矩阵分解来寻找特征基矩阵，然后根据所得到的系数矩阵确定细胞所属类别，最后通过无监督聚类方式获得单细胞测序数据集的分类^[21]。除上述方法外，还可以将数据降维和通用的聚类方法结合起来进行聚类，例如首先使用 t-SNE 算法将高维数据嵌入到低维流形中，然后在低维空间中使用 k-均值聚类算法进行数据聚类^[22]。此外，通过机器学习的方法^[48-49]或者分析细胞特异性基因调控网络^[50]也可以用于识别细胞的分类。

3.1 聚类分析的基础

3.1.1 样本间距离与相似度

聚类分析的核心是将相似的样本分为一个类，而不相似的样本分为不同的类。通俗地说，聚类就是将数据分类到不同的类或簇，使得同一个簇中的样本有很大的相似性，不同簇间的样本相似性较低。样本间的相似性通常可以通过样本间的距离或者相似度进行定义，因此样本距离或相似度的定义在聚类分析中起关键作用。

令 X={x₁，···，x_m}表示 m 个样本组成的样本集，其中

x_{i} \in R^{n}

表示一个样本点，含有 n 个指标。则样本集组成

R^{n}

中的点集 Ω。对这个点集，可以定义 Ω 上的距离 d:Ω×Ω→

R^{}

来量化表示样本之间的相似性。

在数学上，称向量空间的二元实函数 d:

Ω \times Ω \mapsto R

为距离函数，如果对任意 x，y，z∈Ω，d（x，y）满足以下三条性质：

1）非负性，即

d (x, y) ⩾ 0

当且仅当 x=y 时等号成立；

2）对称性，即

d (x, y) = d (y, x);

3）三角不等式，即

d (x, z) ⩽ d (x, y) + d (y, z) .

通常，在进行数据分析以前，需要做一些数据标准化和规范化处理。特别地，在进行距离计算以前，需要检查数据之间的量纲是否统一。因为不同的量纲会影响数据的取值，同时影响样本间的距离计算结果。在下面的介绍中，总假设已经对数据进行了标准化处理，否则，按照前面介绍的方法进行数据标准化处理即可。

在实际计算中，可以采用不同的距离定义来进行计算，距离越小表示相似度越大。常用的距离有闵可夫斯基距离（Minkowski distance）。样本 x，y的闵可夫斯基距离定义为

d (x, y) = ‖ x - y ‖_{p} = {(\overset{m}{\underset{i = 1}{Σ}} {|x_{i} - y_{i}|}^{p})}^{\frac{1}{p}}

(16)

这里的p≥1。

当 p=2时的闵可夫斯基距离即为欧氏距离（Euclidean distance），即对应于两点间坐标差的平方和再开方

d_{2} (x, y) = {(\overset{m}{\underset{i = 1}{Σ}} {|x_{i} - y_{i}|}^{2})}^{\frac{1}{2}} .

当 p=1 时称为曼哈顿距离（Manhattan distance），即对应坐标差的绝对值之和

d_{1} (x, y) = \overset{m}{\underset{i = 1}{Σ}} |x_{i} - y_{i}|

当

p = + \infty

时称为切比雪夫距离（Chebyshev distance），即取各个坐标数值差的绝对值最大值。

d_{\infty} (x, y) = \underset{i}{m a x} |x_{i} - y_{i}| .

上面的欧氏距离还可以推广到更一般的情况

\begin{matrix} d_{2} (x, y) = {(\overset{}{\underset{i, j}{Σ}} g_{i j} (x_{i} - y_{i}) (x_{j} - y_{j}))}^{\frac{1}{2}} \\ = \sqrt{(x - y)^{T} G (x - y)}, \end{matrix}

其中 G=（g_ij）为对称正定矩阵。特别地，如果取系数矩阵为G=Σ^-1，其中 Σ 为样本集的协方差矩阵，则称为马氏距离（Mahalanobis distance）。马氏距离是在机器学习中常用的距离指标，可以看做是欧氏距离的一种修正，修正了欧式距离中各种维度不一致且相关的问题。

不同距离的定义在具体应用时都有不同的优缺点。欧氏距离使用起来很直观，计算机实现也比较简单，在许多应用中都显示出了很好的效果。在低维空间中，使用欧氏距离来度量距离，一些聚类算法就会表现出很好的效果。但需要注意，欧氏距离没有考虑分量之间的相关性，单一特征的多个分量会干扰计算结果。此外，欧氏距离还可能会随着特征的单位变化而有所偏斜。因此，在使用欧氏距离之前，通常需要对数据进行归一化以消除单位变化的影响。此外，随着数据维度的增加，欧几里得距离的作用变小。而切比雪夫距离也受到高维“诅咒”所影响，当数据的维度很高时，可能会导致距离计算不准确。此外，切比雪夫距离对异常值比较敏感，因为它是取各个坐标数值差的绝对值的最大值，如果某个坐标上的数值特别大或特别小，会对距离计算产生较大影响。在一些聚类算法中，切比雪夫距离可能会导致聚类结果不稳定，因为它只考虑了各个坐标数值的最大差异，而忽略了不同维度之间的相关性。所以，切比雪夫通常应用于非常特殊情况，这使得它很难像欧几里得距离或余弦相似性那样作为一个通用的距离度量。出于这个原因，通常只在非常确定它适合的情况下才使用。

在样本空间中，两个样本点之间的距离越近表示数据点越相近，更加倾向于表示同一类细胞。除了距离以外，还可以通过相似度来表示数据之间的关联程度或者相似性。相似度也可以通过数据信息来定义，但是跟距离不同，两个样本点的相似度越大表示某种特征越相近。对样本间的相似度有不同的方式进行定义。

皮尔逊相关系数（PCC）是定义两个样本关联程度的常用指标。设 X和 y是对应于两个样本特征的向量，它们的皮尔逊相关系数的定义为

P C C (x, y) = \frac{\overset{m}{\underset{i = 1}{Σ}} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\overset{m}{\underset{i = 1}{Σ}} {(x_{i} - \bar{x})}^{2}} \sqrt{\overset{m}{\underset{i = 1}{Σ}} {(y_{i} - \bar{y})}^{2}}},

其中

\bar{x}

和

\bar{y}

分别表示向量 X 和y的分量的平均值。相关系数的取值范围为[-1，+1]。皮尔逊相关系数具有位移不变性和尺度不变性，经常用来衡量两个样本之间的关联程度。

类似于皮尔逊相关系数，可以定义两个向量 X和 y 的夹角余弦作为相似度的度量，即

c o s θ = \frac{\overset{m}{\underset{i = 1}{Σ}} x_{i} y_{i}}{\sqrt{\overset{m}{\underset{i = 1}{Σ}} x_{i}^{2}} \sqrt{\overset{m}{\underset{i = 1}{Σ}} y_{i}^{2}}}

需要注意，余弦相似度的特点是不考虑向量的大小，只考虑其方向，这意味着数据值的差异没有被完全考虑。当我们有高维数据且向量的大小并不重要时，可以使用余弦相似度来刻画样本的相似性。

通过样本间的欧氏距离d₂（x，y），可以利用高斯核函数定义样本点 X和 y 之间的相似度为

W (x, y) = e x p (- \frac{d_{2} (x, y)}{2 σ^{2}}) .

高斯相似度可以用来表示样本点 y 在 X的邻域中的概率。

在数据聚类中，不同的距离或者相似度的度量可以得到不同的结果。所以，在进行聚类分析时选择合适的距离或相似度是十分重要的。需要注意的是，单细胞转录组数据具有高维的特点，因此，当主要关心单个细胞间的基因表达模式而非具体表达量时，可以采用余弦相似度来度量距离。

3.1.2 类与类间距离度量

在进行数据聚类时，还需要计算类与类之间的距离。类与类之间的距离有多种定义方式，下面介绍几种常见的定义。

以 G 表示类或簇（Cluster），x_i∈G 表示类中的样本，N（G）表示类G 中样本的个数，x_G表示类 G 的重心或质心，即

x_{G} = \frac{1}{N (G)} \underset{x \in G}{Σ} x,

记 D（G_p，G_q）为两个类 G_p与类G_q之间的距离，也称为连接（Linkage）。下面是几种关于连接的常用定义方式：

1）单连接法（Single linkage）：把距离 D（G_p，G_q）定义为类G_p 中的样本与G_q 中的样本之间距离的最小值，即类间距离最近的两个样本的距离

D (G_{p}, G_{q}) = m i n \{d (x, y) ∣ x \in G_{p}, y \in G_{q}\} .

2）完全连接法（Complete linkage）：把距离D（G_p，G_q）定义为类G_p中的样本与G_q中的样本之间距离的最大值，即类间距离最远的两个样本的距离

D (G_{p}, G_{q}) = m a x \{d (x, y) ∣ x \in G_{p}, y \in G_{q}\} .

3）重心法（Centroid method）：把距离 D（G_p，G_q）定义为类 G_p 的重心与类G_q的重心之间的距离，即

D (G_{p}, G_{q}) = d (x_{G_{p}}, x_{G_{q}}), x_{G} = \frac{1}{N (G)} \underset{x \in G}{Σ} x, (G = G_{p}, G_{q}) .

4）平均连接法（Average linkage）：把距离 D（G_p，G_q）定义为类G_p与类G_q中任意两个样本之间距离的平均值，即类间所有样本对的距离的平均值。

D (G_{p}, G_{q}) = \frac{1}{N (G_{p}) N (G_{q})} \underset{x \in G_{p}}{Σ} \underset{x \in G_{q}}{Σ} d (x, y) .

如果将类间所有样本对的距离的平均值换为中位数，即是中间连接法（Median linkage）。

5）离差平方和法（Ward method）：该方法源自方差分析思想，若样本分类正确，类内的离差平方和应该较小而类间的离差平方和应该较大。设类G_p 中所有样本的平均值为

\bar{x} = {({\bar{x}}_{p 1}, \dots, {\bar{x}}_{p m})}^{T},

则G_p的类内离差平方和为

W_{p} = \sum_{i \in G_{p}} \sum_{j = 1}^{m} {(x_{i j} - {\bar{x}}_{p j})}^{2} .

若把G_p 和G_q 合并，记为类 G_c，则定义 G_p 与G_q 的Ward距离为

W_{c} - (W_{p} + W_{q}),

即合并造成的类内离差平方和的增量。

在实际应用中，不同的类与类之间距离定义并无好坏之分，不同的定义有其所使用的数据类型和目标。因此，在应用中，通常需要根据数据本身的内涵选择合适的距离定义进行聚类分析。有时，可以比较不同的计算方法，选择出符合预期结果的距离定义。

3.2 常见的聚类算法

上面给出了样本与样本之间的距离和类与类之间距离的定义。下面介绍几种在单细胞转录组数据中被广泛使用的聚类方法，分别是 k-均值聚类算法（k-means clustering）^[51]、层次聚类法（Hierarchical clustering）、基于图的社区检测算法^[52]。k-均值聚类是单细胞数据一致聚类算法（SC3）的基础^[22]，层次聚类法是目前使用最广泛的一种聚类分析算法，而基于图的社区检测算法则已经被应用到经典的单细胞数据分析平台 Seurat^[18]和 Scanpy^[53]中。

3.2.1 k-均值聚类

k-均值（k-means）聚类算法是一种迭代求解的聚类算法^[51]，其主要思想是在每次迭代计算中都将样本点分配到“最近”的一类中。在该方法中，k 是超参数，表示预先设定好的类的数目。k-均值聚类的策略是通过损失函数的最小化选取最优的划分。

为进行k-均值聚类，首先需要定义损失函数。采用欧氏距离平方（Squared euclidean distance）作为样本之间的距离

d (x_{i}, x_{j}) = {‖x_{i} - x_{j}‖}^{2}

则可以把综合损失函数定义为所有样本与其所属类的中心之间的距离的总和，即

\begin{matrix} W (C) = \overset{k}{\underset{l = 1}{Σ}} \underset{x \in C_{l}}{Σ} d (x, x_{o} (C_{l})), \\ x_{o} (C_{l}) = \frac{1}{N (C_{l})} \underset{x \in C_{l}}{Σ} x . \end{matrix}

这里C_l 表示第l 个类， C={C₁，C₂，···，C_k}表示对样本的一个聚类，N（C_l）表示类C_l 中的元素个数。根据上面的叙述， k-均值聚类就是求解如下最优化问题：

\underset{C}{m i n} W (C) .

k-均值聚类是一种贪心算法。所谓贪心算法是指在问题求解时总是做出在当前看来是最好的选择，因此很容易收敛到局部最优解。此外，超参数k可以利用 Gap 统计量或者轮廓系数来确定。

k-均值聚类方法已被广泛应用到单细胞转录组数据分析的不同算法中，然而不同的算法各有优缺点。例如，SAIC 算法^[54]利用迭代 k-均值聚类方法来识别将细胞分成不同簇的特征基因最佳子集，其不足是对离群点很敏感；pcaReduce 算法^[55]是一种层次聚类方法，它将k-均值聚类结果作为初始聚类，然而该方法的结果不够稳定；RaceID 算法^[56]应用k-均值聚类揭示了罕见肠细胞类型的异质性，但不适用于非稀有细胞类型。为了克服上面所提算法的缺点，SC3^[22]将k-均值聚类结果与不同的分类条件相结合，得到了更高的准确度。RaceID2^[57]采用k-中值聚类代替了k-均值聚类。k-中值聚类使用一阶皮尔逊相关性作为聚类距离度量，代替欧氏距离。RaceID3^[58]作为RaceID2的高级版本，增加了特征选择，并引入随机森林方法来对k-均值聚类结果重新分类。

3.2.2 层次聚类法

层次聚类方法包括两种方式^[59]:①自下而上的凝聚层次聚类，即一开始每一个个体都是一个类，然后根据类与类之间的距离不断合并，最后形成一个“类”；②自上而下的分裂层次聚类，即一开始所有个体都属于一个类，然后根据个体之间的距离不断地进行类的分裂，最后每个个体都是一个“类”。下面给出凝聚层次聚类和分裂层次聚类法的算法流程：

在这里，样本之间的距离通常取为欧氏距离，类与类之间的距离通常取为最短距离（单连接）。当然，也可以选择其他的连接方式和样本距离定义，具体选择需要根据样本数据的类型来确定。

层次聚类法通过在细胞/基因之间建立了一个层次结构，在发现小簇的稀有细胞类型方面表现突出。层次聚类法不需要预先确定聚类的数量，也不需要对单细胞转录组数据的分布做假设。因此，层次聚类也在单细胞转录组数据聚类方法中被广泛应用。例如，CIDR^[60]整合了数据降维和层次聚类，将其应用到单细胞转录组数据分析中，使用隐式插补过程来处理缺失效应，实现了细胞间距离的稳定估计；BackSPIN^[61]是一种基于分裂层次聚类与将样本点划分到邻域的双聚类方法，实现同时基因和细胞的聚类；pcaRedcuce是一种基于主成分分析降维的凝聚层次聚类方法，以层次结构提供聚类结果；SINCERA^[62]采用中心化的皮尔逊相关性作为距离的层次聚类，并使用平均链接方法来识别细胞类型。

3.2.3 谱聚类

谱聚类算法是基于图论的知识所演化出来的计算方法^[63]，在聚类中广泛使用。主要思想是将所有样本数据看成空间中的点，所有点之间通过加权边连接起来构成一个无向图。然后对连边的权重进行赋值使得距离较远的两点之间边的权重较低，而距离较近的两点之间边的权重较高。然后对所有数据点所组成的图进行切图，使得切图以后不同子图间边的权重之和尽可能低，而子图内边的权重尽可能高，从而达到聚类的目的。

在谱聚类算法中，可以采用不同的方法来定义两点之间连边的权重，即数据点之间的邻接矩阵。对于数据点x_i和x_j，首先通过两点之间的距离

s_{i j} = {‖x_{i} - x_{j}‖}^{2}

构建距离矩阵 S=（s_ij），然后通过距离矩阵构建邻接矩阵。构建邻接矩阵的常用方法有三种：

ϵ

-近邻法、k-近邻法和全连接法。

对于

ϵ

-近邻法，设置一个距离阈值

ϵ

，然后通过该阈值和距离s_ij定义邻接矩阵 W中的权重如下：

w_{i j} = \{\begin{matrix} 0, s_{i j} > ϵ \\ ϵ, s_{i j} ⩽ ϵ . \end{matrix}

对于 k-近邻法，利用 k-近邻网络（KNN）算法遍历所有样本点，取距离每个样本最近的 k 个点作为近邻，然后设置和样本点 i 最近的 k 个点之间的邻接系数 w_ij＞0。然而，由这一方法所得到的权重不是对称的。为了解决这一问题，采用以下方法进行修正。第一种k-近邻法是只要一个点在另一个点的 k 近邻中就设为w_ij＞0，即

w_{i j} = w_{j i} = \{\begin{matrix} 0, & x_{i} \notin K N N (x_{j}) and x_{j} \notin K N N (x_{i}) \\ e x p (- s_{i j} / 2 σ^{2}), & x_{i} \in K N N (x_{j}) or x_{j} \in K N N (x_{i}) . \end{matrix}

第二种 k-近邻法是必须两个点互为 k-近邻时，才设置w_ij＞0，即

w_{i j} = w_{j i} = \{\begin{matrix} 0, & x_{i} \notin K N N (x_{j}) or x_{j} \in K N N (x_{i}) \\ e x p (- s_{i j} / 2 σ^{2}), & x_{i} \in K N N (x_{j}) and x_{j} \in K N N (x_{i}) . \end{matrix}

在全连接法中，设置所有点之间的权重都大于 0，并根据距离定义其权重，即认为所有点之间都是相邻的。这一方法是使用最普遍的。全连接法中边的权重系数通过作用于距离s_ij的核函数来实现，常用的核函数包括多项式核函数，高斯核函数和 Sigmoid 核函数。最常用的是高斯核函数 RBF，此时对应的权重为

w_{i j} = e x p (- s_{i j} / (2 σ^{2}))

通过邻接矩阵 W=（w_ij），就可以构成一个无向图以进行谱聚类算法操作了。为了描述具体的操作方法，还需要定义两个矩阵，分别是度矩阵和拉普拉斯矩阵。

首先通过上面的邻接矩阵 W 定义度矩阵。对每个数据点x_i，定义相应的度d_i为与x_i相邻的所有数据点的权重之和，即

d_{i} = \overset{m}{\underset{j = 1}{Σ}} w_{i j}

根据权重d₁，d₂，···，d_m，定义相应的度矩阵为对角阵

D = d i a g (d_{1}, d_{2}, \dots, d_{m}) .

然后，通过上面的邻接矩阵 W 和度矩阵 D，定义拉普拉斯矩阵为 L=D-W。拉普拉斯矩阵具有一些比较好的性质，分别为：

1）L是对称矩阵；

2）L的所有特征值都是实数;

3）对于任意向量 f，有

f^{T} L f = \frac{1}{2} \overset{m}{\underset{i, j = 1}{Σ}} w_{i j} {(f_{i} - f_{j})}^{2}

拉普拉斯矩阵L是半正定的，并且对应的 n 个实特征值都大于或等于0，最小的特征值为 0。

通过上面的邻接矩阵定义了一个无向带权图 G=（V，E），其中 V=（v₁，···，v_m）表示顶点集合（这里用 V 表示图中的顶点集，也即对应于数据点），E 表示边的集合。下面可以进行切图操作。

切图操作的目的是把顶点集 V 分割为不相交的子集 A₁，A₂，···，A_k使得

A_{i} \cap A_{j} = \emptyset, ⋃_{i = 1}^{k} A_{i} = V .

对任意两个子图 A 和 B，定义它们之间的权重为

W (A, B) = \underset{v_{i} \in A, v_{j} \in B}{Σ} w_{i j} .

对于包含 k 个子图（A₁，A₂，···，A_k）的切图方案，定义相应的目标函数为

c u t (A_{1}, A_{2}, \dots, A_{k}) = \frac{1}{2} \overset{k}{\underset{i = 1}{Σ}} W (A_{i}, {\bar{A}}_{i}),

其中

\bar{A}

表示顶点集A的补集。切图的目标是对给定的参数 k，极小化上面的目标函数。

下面的算法通过谱聚类方法进行切图，找到最优化方法，主要的思想是先通过对拉普拉斯矩阵的特征分解进行数据降维，然后在低维空间中使用其他聚类算法进行聚类。算法流程如下：

谱聚类的本质思想是从数据中构造某种相似矩阵，然后对矩阵进行特征分解，去掉冗余信息，然后进行投影（数据降维），提取主要成分，最后对降维以后的数据采用其他聚类方法进行聚类。简单地说，就是先降维、再聚类。

谱聚类是近年来才被广泛使用的聚类方法，通过依赖细胞相似性矩阵的特征值来适应数据分布。SIMLR^[18]是一种基于谱聚类，专为单细胞转录组数据设计的方法，用于单细胞转录组数据的降维、聚类和可视化，SIMLR 在处理噪声较大的大规模数据集时具有优势。

3.2.4 基于模块度的 Louvain 聚类算法

基于模块度的Louvain聚类算法^[64]是一种基于图论的算法，其主要思想是通过最优化模块度的目标函数，使得划分的类模块度最大。模块度（Modularity）是用于表示样本数据划分群能力的量化指标，取值范围在-1到 1之间，数值越大，表示一个分群（Group）更加紧凑。

为了量化表示一个聚类结果的模块度，首先建立包含所有样本点的无向图 G=（V，E）。这里为简单记，以节点 v_i 表示数据集中的样本点 x_i，则节点集 V={v₁，v₂，···，v_m}。为建立节点间的连边关系 E，根据节点间的距离或者相似度并依据给定的阈值构建节点之间的连接关系。例如，以距离为例，如果距离 d（v_i，v_j）＜d_crit，则认为节点 v_i 和 v_j 之间存在边，这里 d_crit 为给定的阈值。对于按此规则定义的无向图，令 A=（a_ij）为相应的邻接矩阵，即当节点 v_i 和 v_j 直接连接时 a_i_，_j=1，否则 a_i_，_j=0。记所有边的集合为 E，并令 M 表示边的总数，即

M = \frac{1}{2} \underset{i, j}{Σ} a_{i, j}

根据邻接矩阵，可以计算出每个节点的度，即与该节点相连的边的数量。节点 v_i 的度 d_i 定义为

d_{i} = \underset{j}{Σ} a_{i, j}

根据上面所构建的无向图，如果根据聚类算法得到节点的类为 {C₁，C₂，···，C_k}，则对应的模块度的计算公式为

Q = \frac{1}{2 M} \underset{1 ⩽ i, j ⩽ m}{Σ} (a_{i, j} - \frac{d_{i} d_{j}}{2 M}) δ (v_{i}, v_{j})

(17)

其中，δ（v_i，v_j）表示节点 v_i 和 v_j 是否在同一个类中，定义为

δ (v_{i} ， v_{j}) = \{\begin{matrix} 0 ， v_{i} ， v_{j} 在 同 一 个 类 中 \\ 1 ， v_{i} ， v_{j} 不 在 同 一 个 类 中 . \end{matrix}

根据公式（17），对每个类中的点进行合并计算，则可以简化为

Q = \overset{k}{\underset{i = 1}{Σ}} (\frac{E_{i}}{M} - {(\frac{D_{i}}{2 M})}^{2})

其中 E_i 表示类 C_i 内部的边数，D_i 表示类 C_i 中所有节点的度数之和。

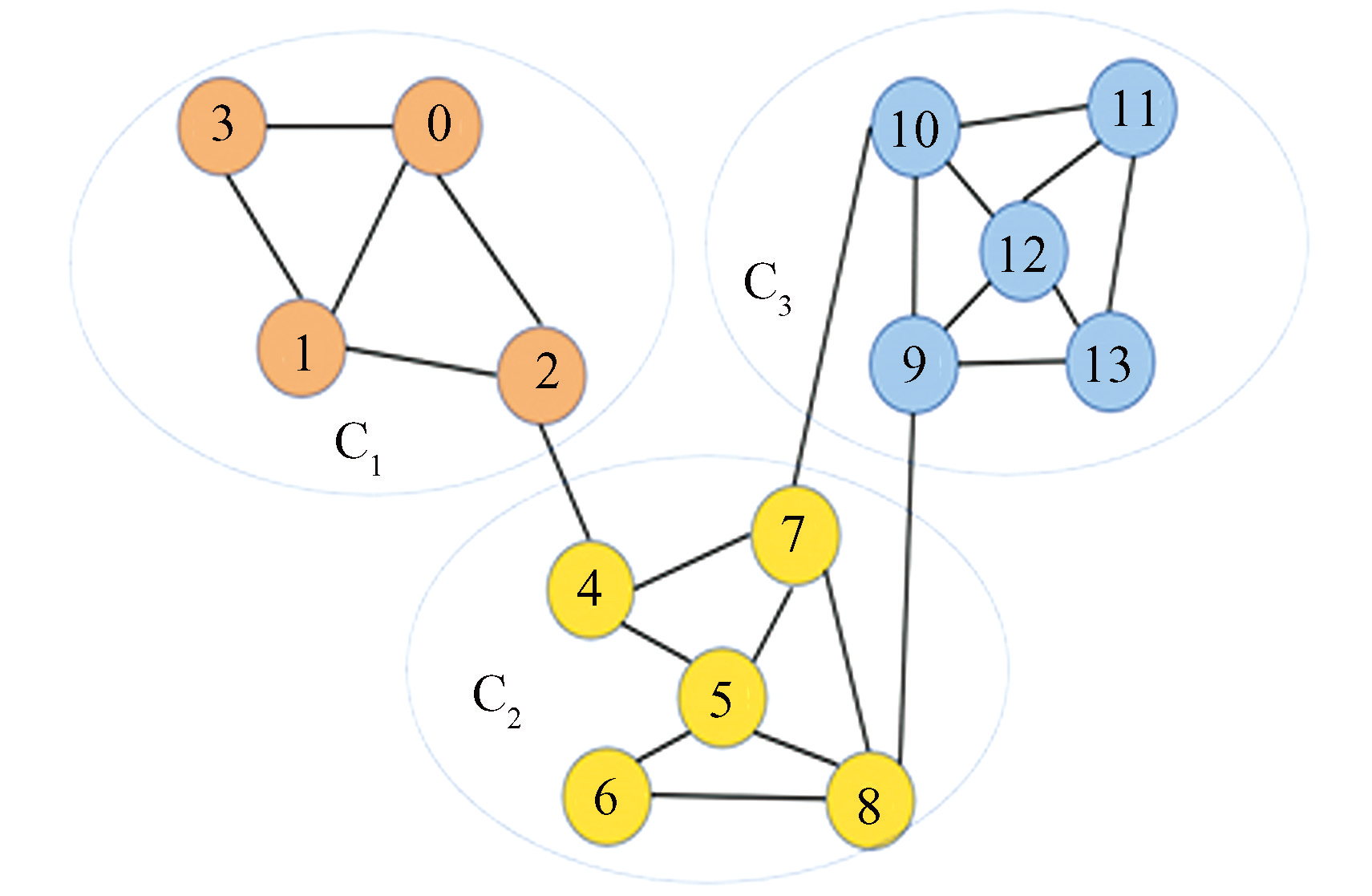
图7模块度计算示例

Fig.7Example of module degree calculation

下面以图7所示的数据分类结果为例说明模块度的计算过程。在图中有三个类，其中 C₁ 包含 5 个节点，5 条内部的边，所有节点的度数之和为11，所以 E₁=5，D₁=11。类似地，有E₂=7，D₂=17，E₃=8，D₃=18。此外，图中共有 23 条边，所以 M=23。由此，对应的模块度为

Q=5/23+7/23+8/23- (11/46) ²- (17/46) ²- (18/46) ²=0.523.

根据模块度的定义，可以进行聚类结果的选择。下面以 k-均值聚类方法为例说明操作过程。首先设置 k=1进行 k-均值聚类，然后对聚类结果计算模块度。然后令 k=k+1 并进行相应的 k-均值聚类和模块度计算。如果模块度增加，则令 k=k+1 并继续进行，直到模块度开始减少为止。取模块度最大所对应的 k 值的结果作为最优的聚类结果。

由于k-均值聚类和层次聚类方法在大规模数据集上的局限性，基于社区检测的聚类近年来越来越受欢迎。社区检测在可以用带节点和边的图进行表示的系统中至关重要。对于单细胞转录组数据，节点指代细胞，边缘权重由细胞间的距离表示。Louvain 算法是最流行的社区检测算法，被广泛应用于单细胞转录组数据聚类。SCANPY^[53]是一个基于Python语言的可扩展单细胞RNA-seq分析工具包，其聚类部分就是Louvain算法；基于R语言的单细胞分析工具包Seurat^[18] 应用Louvain算法对细胞类型进行聚类。总之，基于Louvain 算法的聚类算法的优点是适合大规模数据。

3.3 聚类分析的应用

3.3.1 细胞类型的确定

根据单细胞测序数据对细胞进行聚类后，需要根据每个类的特征表达基因识别细胞的类型。为此，从数据处理的角度，需要确定差异表达基因，也即找出在一个类中与其它类表达有明显差异的基因。然后，将所识别出来的差异表达基因与先验知识进行比较以确定细胞类型。对于细胞类型的识别需要一定的先验知识，了解样本组织中主要包含哪些类型的细胞，和每一类细胞的特征表达基因等。例如，示例数据集 pbmc3k来源于外周血细胞，细胞类型主要是包括血细胞和成熟的免疫细胞，包括T 淋巴细胞、B 淋巴细胞、浆细胞、天然杀伤细胞等。通过查阅文献或者数据库，可以收集到这些细胞类型的标记基因，从而确定聚类结果的具体细胞类型。

通常可以采用统计方法识别出差异表达基因，常用的统计方法有T检验（t-test）、贝叶斯T-检验（Bayes t-test）、秩和检验（Wilcoxon rank sum test）等。在这里主要给出两样本秩和检验的基本原理。

假设有两组样本点 X={X₁，X₂，···，X_m} 和 Y={Y₁，Y₂，···，Y_n}，秩和检验主要想回答的问题是样本点 X 和 Y 是否有显著差异。为此，假设 X 和 Y 满足相同形式的分布 F，均值分别为μ₁和 μ₂，那么要检验的问题为

\begin{matrix} H_{0} : μ_{1} = μ_{2} \\ H_{1} : μ_{1} \neq μ_{2} . \end{matrix}

为进行上述检验，首先将样本 X 和 Y 混合在一起，然后按照从小到大的顺序排列起来得到数据序列 Ω。令R_i记 Y 中样本点 Y_i 在混合序列Ω中的秩，即在所有样本中从小到大排列的“位置”，表示为

R_{i} = # \{X_{j} < Y_{i}, j \in I_{X}\} + # \{Y_{k} ⩽ Y_{i}, k \in I_{Y}\},

其中I_X表示集合X的指标集， I_Y表示集合Y的指标集，# 表示集合中元素的个数。令

W_{Y} = \overset{n}{\underset{i = 1}{Σ}} R_{i},

表示样本集 Y 的秩和。同样地，对样本集X 也可以计算相应的秩和W_X，称W_X和W_Y为Wilcoxcon 秩和统计量。

可以通过 Wilcoxcon 秩和统计 W_X 和W_Y判断两个数据集X和Y是否有显著差别。例如，如果Y 的数据普遍比X的数据小，则明显有W_Y＜W_X。如果 W_Y＜W_X 则可以排除原假设，认为数据集X和 Y 是有显著差别的，否则不能认为 X 和 Y 有显著差别。

根据上面的公式容易得到

W_{Y} = \{X_{j} < Y_{i} ， j \in I_{X} ， i \in I_{Y}\} + \frac{n （ n + 1 ）}{2}

，和

W_{X} = \{Y_{j} < X_{i} ， j \in I_{Y} ， i \in I_{X}\} + \frac{m （ m + 1 ）}{2} .

由于 m 和 n 都是常数，可以省略。因此，记

\begin{matrix} W_{X Y} = # \{X_{j} < Y_{i}, j \in I_{X}, i \in I_{Y}\}, \\ W_{Y X} = # \{Y_{i} < X_{j}, j \in I_{X}, i \in I_{Y}\} . \end{matrix}

则在原假设 H₀之下，W_XY与 W_YX同分布，称之为 Mann-Whitney 统计量。可以看到，Wilcoxon 秩和统计量与 Mann-Whitney 统计量是等价的，因此两样本的秩和检验也被称为 Wilcox-Mann-Whitney 检验。

3.3.2 Doublet的去除

在前面关于数据预处理的步骤中，介绍了使用 nCount 作为指标，过滤掉 doublet/multiplet 的方法。然而，这样“一刀切”的方式过于简单粗暴，容易产生错误。而在下游的数据处理中， doublet/multiplet 的存在可能会极大影响 scRNA-seq 数据的分析和解释，不适当保留的 doublet/multiplet 会导致“新”的细胞亚群产生，干扰后续的结果分析。然而，准确地去除doublet信号的方法存在几点挑战：① 尽管doublet/multiplet 应该具有特别的基因和独特分子标识符（UMI）的分布，具有两倍及以上的 RNA 含量，但这些变量不足以准确地识别单个细胞的信号是否为双重态的; ② 不同的 RNA 丰度和/或合成 cDNA 中的技术差异可能导致每个细胞信号的贡献不均。所以，若简单地认为 doublet 中两个不同细胞的贡献程度相同可能会过于简单。

关于 scRNA-seq 数据中 doublet 的过滤，目前已提出一些常用的统计学方法，例如DoubletDecon^[65]，Scrublet^[66]和 DoubletFinder^[67]，用来识别和过滤 doubleblet。虽然现已有多种去除 doublet 的算法，各种算法的步骤不同，但是总体的思路大致是一样的。DoubletDecon 方法基于反卷积（Deconvolution）的策略，可以实现在保留过渡细胞状态的同时去除异型 doublet，而 Scrublet 和 DoubletFinder 都是通过最近邻居（Nearest neighbor）策略来检测 doublet。

DoubletFinder在识别 doublet 的算法中比较具有代表性，具体的算法原理可以参考原文，这里给出算法思路以及数学描述。

DoubletFinder算法的主要思路可以分为4个步骤：① 生成虚拟的 doublet，即假设 doublet 的基因表达谱是由两种不同类型细胞的基因表达谱的平均值构成；② 将生成的虚拟 doublet 样本集与原始样本数据集合并；③ 执行 PCA 降维，然后计算降维以后的数据所对应的距离矩阵；④ 根据距离矩阵进行聚类，计算出每个细胞类中虚拟 doublet 所占的比例，超过某个阈值就认定该细胞类中的真实细胞数据为 doublet。

下面用数学语言对上面思路进行描述。假设已经对原始数据完成聚类这个步骤，即每个原始数据集中的细胞都属于确定的细胞类。设共有 N 个细胞，被分为了 s 个细胞类。使用集合 C_i 表示属于C_i类的细胞，共有 n_i 个细胞，即

C_{i} = \{{c e l l}_{i 1} ， {c e l l}_{i 2} ， \dots ， {c e l l}_{i n_{i}}\} ， i = 1 ， \dots ， s

1）通过随机选择任意两个不同类型的真实细胞，将其基因表达谱的均值作为新生成的虚拟doublet。例如，用 x_i₁，x_i₂表示随机选择的两个细胞 cell_i₁，cell_i₂的基因表达向量（原始计数矩阵中的数据），那么使用 cell_i₁，cell_i₂生成的模拟doublet的基因表达向量表示为

x_{1}^{*}

，则

x_{1}^{*} = \frac{1}{2} (x_{i 1} + x_{i 2}) .

使用上述的方式生成M个虚拟的doublet细胞，

M = ρ N, ρ = 1 / 4

2）将真实的细胞数据集和虚拟生成的doublet细胞数据集合并为新的数据集 X，

X = [x_{1}, x_{2}, \dots, x_{N}, x_{1}^{*}, x_{2}^{*}, \dots, x_{M}^{*}],

对合并的数据集作预处理，包括标准化、归一化和高变基因的挑选，最终得到处理后的数据集 X。

3）对合并处理后的数据集 X 作主成分分析降维，产生降维后的数据集 H，每一列表示一个细胞。根据数据集 H计算降维后的细胞间欧几里得距离矩阵D，

D = [\begin{matrix} d_{1, 1} & \dots & d_{1, M + N} \\ ⋮ & ⋱ & ⋮ \\ d_{M + N, 1} & \dots & d_{M + N, M + N} \end{matrix}]

其中 d_i_，_j表示经 PCA 降维后第i个细胞与第 j 个细胞的欧氏距离。

4）根据距离矩阵 D 并采用聚类算法得到新的细胞类，计算每一个细胞类中虚拟 doublet 所占的比例 ρ_ANN，

ρ_{A N N} = \frac{N_{i}^{*}}{N_{i}},

其中，

N_{i}^{*}

表示第i 个细胞类中虚拟的 doublet 细胞的数量，N_i 表示第i 个细胞类中所有细胞的数量。

如果某个细胞类中虚拟 doublet 所占的比例 ρ_ANN 超过给定的阈值k，则认为该类为doublet 细胞类，即所有细胞均为 doublet。需要注意的是，这里的阈值k 需要研究者根据实际情况确定。

与DoubleFinder 算法的基本思路类似，DoubletDecon 算法的过程分为三个步骤：① 合成 doublet 表达谱（合成细胞簇的表达谱），即合并转录情况相似的细胞簇；② 创建每个细胞的反卷积细胞谱（deconvoluntion cell profile，DCP）。细胞谱矩阵中的每一列代表一个细胞，每一列中的每个元素的取值表示不同参考细胞对该细胞的贡献值所占的百分比，每一列的和为100%; ③ 将原始细胞中 DCP 与合成细胞簇的 DCP 最相似的细胞定义为 doublet。

虽然 DoubleFinder 和 DoubletDecon 这两个算法的过程有区别，但总体思路都是先构建虚拟的 doublet，然后将那些与虚拟 doublet 相似的细胞定义为 doublet。

3.3.3 伪时间分析

单细胞数据集的伪时间分析（Pseudotime analysis）也被称为细胞轨迹推断（Trajectory inference，TI），即根据细胞之间表达模式的相似性对单个细胞沿着轨迹进行排序，构建细胞间的变化轨迹来重塑细胞随着时间的变化过程，从单细胞水平推断细胞间的演化及分化过程。细胞的伪时间分析在组织发育、疾病免疫细胞演化、细胞谱系分化等研究中起到很重要的作用。需要注意的是，这里的时间并不是真正的时间，而是一个虚拟的时间，是指细胞与细胞之间的转化和演替的顺序和轨迹。机体为了响应各种应激，其细胞会从一种功能“状态”转变为另一种功能“状态”。当一个细胞在不同状态之间转变时，往往会经历转录重组，导致一些基因被沉默，另一些基因被激活。但是，在实验中筛选这些具有瞬态变化的细胞是十分困难的，而单细胞转录组数据为描述细胞瞬态变化提供了很好的数据信息。因为细胞的转化过程是连续的，其转化轨迹包含各种状态的细胞，拟时序分析的目的是希望可以根据单细胞测序数据重构细胞状态变化的过程。

伪时间分析包括细胞轨迹分析和细胞谱系分析。细胞轨迹分析是指分析细胞沿着某个过程到达具有特定变化终点的轨迹。细胞轨迹具有简单的树状结构（数据结构），一端是“根”，即起点，另一端是“叶子”，即终点。细胞谱系分析通常指某类祖源细胞在特定条件下具有多个发育轨迹和命运的谱系变化过程，其变化过程类似于复杂树状分支。细胞轨迹分析和细胞谱系分析的原理相似，但是复杂程度有所不同。本文以 Monocle 软件的伪时间分析算法为例，介绍伪时间分析算法的一般步骤。通常情况下，伪时间分析算法一般包括两个步骤：一是降维，二是轨迹建模，其中轨迹建模又可以分为轨迹分区和轨迹图学习两部分。

数据降维的方法包括线性降维方法和非线性降维方法。线性降维方法包括主成分分析（PCA）和独立成分分析（Independent component analysis，ICA）等。非线性降维方法包括t-分布随机流形嵌入（t-SNE），一致流形逼近投影（UMAP）和扩散映射（Diffusion maps，DM）。前文已介绍了 t-SNE 和 UMAP算法，这里简单介绍 DM 算法的思路。在DM 算法中两点之间（细胞之间）的距离是通过概率来计算的。如果两点间的距离较近，则从一个点随机行走到另外一个点的概率就较大。反之，如果两点间的距离较远，则从一个点随机行走到另外一个点的概率就较小。DM算法将距离转换成点与点之间随机行走的概率，并根据这个随机行走的过程捕捉数据间的拓扑结构，以将一个高维数据进行低维展开。

目前，单细胞转录组数据的细胞轨迹分析工具 Monocle 有三个版本。第一个版本叫 Monocle^[68]。在 Monocle 中，假定细胞的分化过程是一个基因表达不断变化的过程，因此细胞间基因表达的相似性反映了他们在这个分化时间轴上的位置关系。Monocle 首先将细胞基因表达水平的高维数据用 ICA 方法进行降维，然后根据细胞之间的相似性采用最小生成树（Minimum spanning tree，MST）的算法构建出所有细胞在二维空间中的位置关系。在这个最小生成树中，Monocle 会找出一条连接最多细胞的最短路径，并根据这条路径计算出拟时间。Monocle 的论文发表在 2014 年，所针对的测序数据是低通量（低细胞数）的轨迹分析。随着测序技术的发展，scRNA-seq 发展到了高通量水平。为了适应高通量的单细胞转录数据，Monocle 系列迎来了第二个版本Monocle2^[27]。Monocle2 依旧是根据细胞间基因表达模式的相似度来计算拟时间，与 Monocle 的不同之处在于它使用主成分分析方法（PCA）进行数据降维，并使用反向图嵌入算法（Reversed graph embedding，RGE）进行轨迹推断。反向图嵌入算法能够获得反映数据隐藏结构的曲线，同时还能得到所有数据点在该曲线上的映射，适用于对大的数据集进行分析。而为了适应更大的数据集，Monocle3^[69]在 Monocle2 的基础上进行了升级，支持在 UMAP 降维算法的基础上进行轨迹推断，除此以外，还可以指定多个“根（Root）”节点，学习“环形”轨迹等。

伪时间分析算法中的降维算法在前文中已经具体介绍，在这里主要说明轨迹建模部分。下面将轨迹建模分为轨迹分区算法和轨迹图学习两个部分展开叙述。对单细胞转录组数据降维得到低维图谱后，Monocle3 使用了一个近似 PAGA^[70]算法，即首先在低维的 UMAP 空间建立基于细胞的 KNN 近邻图。然后使用 Louvain 算法（基于模块度优化的 Louvain 聚类算法）将细胞分组，计算两组细胞间连接的显著程度（这里的零假设为不存在任何连接）。通过这一计算，如果 Louvain 分组比预期中存在更多连接，则将这些连接保留下来，而在 Louvain 算法中不存在的连接则被删除。近似PAGA 算法的结果是细胞集可能会由一个或者多个部分组成，即轨迹分区，每一个部分都会单独进入下一步的轨迹计算。这一步其实是形成概述轨迹图的过程，其中的每个组代表了细胞发展的不同状态。

完成轨迹分区以后，对每个区的数据进行轨迹图学习。下面主要介绍轨迹主图镶嵌算法部分。为了便于理解，这里以构建最小生成树（MST）算法^[71]确定轨迹为例。通过降维、分区两个步骤后，可以得到各个分区里细胞类的中心。将每个分区内细胞类的中心抽象为一个“节点”，各个类中心之间的距离抽象为“边”，由此可以得到由节点和边连接而成的“图（Graph）”。从一个细胞类到另一个细胞类的发育轨迹可以抽象为从一个节点到另一个节点的最短路径，而最小生成树算法正好是在图论中用来寻找连接所有节点的最短路径算法。对于单细胞数据集得到的“图”，轨迹学习可以抽象地理解为寻找最小生成树。

在图论中，对于给定的无向图，如果它的子图中任意两个顶点是互相连通的，并且是一个树状结构，则称这棵树为该图的生成树。当连接顶点之间的边具有权重时，称权重之和最小的树结构为该图的最小生成树。经典的寻找最小生成树的算法有普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。普里姆算法在查找最小生成树的过程中，采用了贪心算法的思想。普里姆算法的思路如下：先构造一个只包含 n 个节点的子图G₀，然后从权重最小的边开始，若它的添加不使 G₀产生回路，则在G₀中加上这条边，如此重复，直到加上 n-1 条边为止。对于包含 n 个顶点的连通图，普里姆算法如下：

在对数据进行降维和聚类的过程中，使用 UMAP 算法将细胞的数据投影到二维空间，就可以在二维平面中得到每一个细胞的坐标，然后根据每个细胞的坐标来创建轨迹和排列细胞。在确定轨迹后，还需要根据聚类结果，指定发育的“根”节点和“叶子”节点，而一个细胞的伪时间值就是它在主干上的投影点到根节点的距离。当然，“根”节点和“叶子”节点的指定需要结合已有的生物学先验知识。盲目地指定根节点和叶子节点所得到的轨迹在研究中意义不大。通过伪时间分析，可以构建细胞状态变化的轨迹，并能找到差异基因的轨迹变化过程，为深入理解不同基因在某类细胞变化过程中的调控作用提供依据。需要注意的是，不是所有样本都适合进行拟时序分析，比如外周血（PBMC）中的细胞几乎都是已经分化成熟的细胞，进行轨迹分析的意义不大。

4 基因拷贝数变异分析

单细胞转录组技术已被广泛应用于解析肿瘤微环境中各种细胞的基因表达水平。进行肿瘤相关的单细胞转录组数据分析的一个重要挑战是如何高效地从肿瘤微环境细胞中识别出恶性肿瘤细胞。

基因拷贝数变异是肿瘤细胞的一个特征。拷贝数变异是基因组结构性变异的一种，一般指基因组片段的拷贝数相对于群体水平的增加或减少，主要表现为亚显微水平的重复或缺失。基因组片段是可以重复的，这种重复的数量称为拷贝数。一般的哺乳动物都是二倍体，而当细胞发生癌变后，拷贝数会发生变化（增加或减少），即发生了拷贝数变异。研究表明鉴别非整倍体（Aneuploid copy number profiles）是区分肿瘤细胞和正常细胞的有效方法，因为非整倍体拷贝数在大部分人类肿瘤中很常见，约占88%，而在具有二倍体基因组的基质细胞类型中不存在^[72]。

这里介绍检测拷贝数变异的算法 CopyKAT^[72]，即非整倍体肿瘤的拷贝数核型分析方法（Copy number karyotyping of aneuploid tumors）。CopyKAT 将贝叶斯方法与层次聚类相结合，利用单细胞转录组数据计算单个细胞的基因组拷贝数分布，进而推断每个细胞是正常细胞还是发生拷贝数变异的细胞（肿瘤细胞）。CopyKAT 的工作流程如图8所示，下面对主要步骤进行详细介绍。

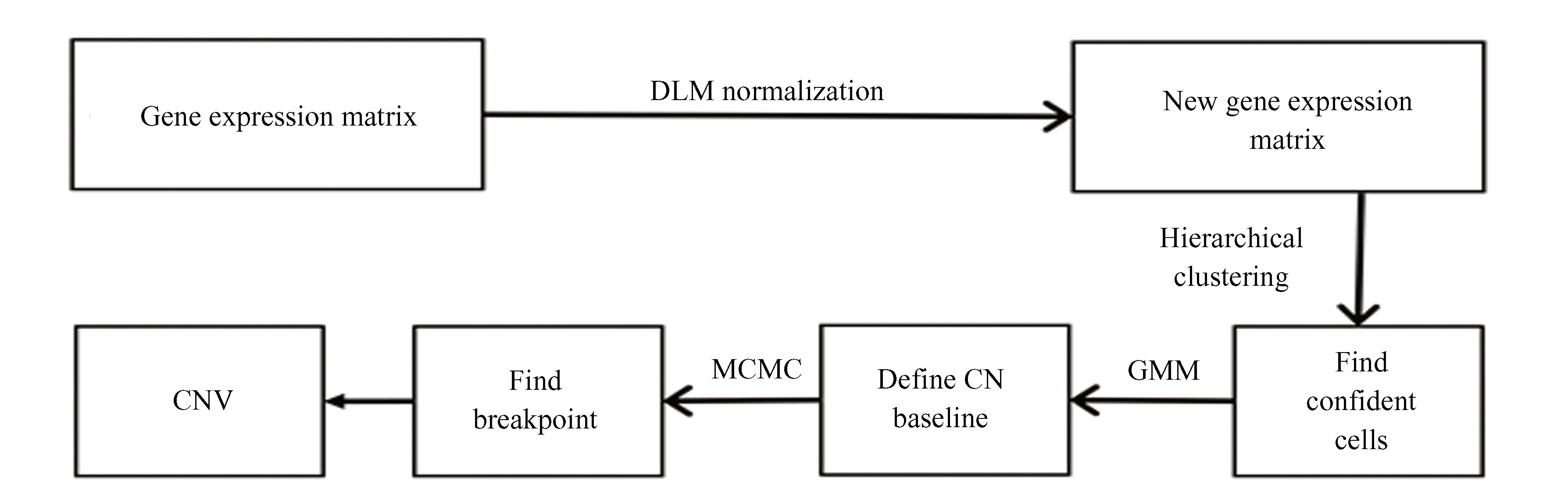
图8CopyKAT 的工作流程

Fig.8Workflow of CopyKAT

4.1 预处理

CopyKAT 的输入是单细胞转录组的基因表达矩阵 X。首先需要移除一些质量不好的细胞数据，将被检测的基因数少于 200 的细胞过滤掉，也就是所保留细胞向量的零范数大于等于 200，即

n {Feature}_{j} ⩾ 200 .

此外，为了消除 droupout 的影响，留下的基因至少要在所有细胞的 5% 中被检测到有表达，且保留的基因数目要多于 7 000 个，而那些在少于 5% 的细胞中表达的基因不在本次分析中考虑。为了能够代表拷贝数，要求每条染色体上至少要有 5 个基因被检测到。另外，为了排除细胞周期相关基因的影响，那些与细胞周期相关的基因也不予考虑。最后，将质控后的所有基因按照基因组中的顺序坐标排序，得到一个新的基因表达矩阵 X。为了平滑方差，对基因表达矩阵 X 做log-Freeman-Tukey 变换，即

X = l o g (\sqrt{X} + \sqrt{X + 1}) .

最后，减小数据间的方差后，再采用多项式动态线性建模方法来平滑基因表达矩阵中的异常值。

4.2 估计二倍体细胞的拷贝数基线值

为了估计基态拷贝数的基线，也就是正常细胞的拷贝数，需要定义一个“自信正常”的细胞子集，即正常二倍体细胞的子集。为此，首先使用层次聚类法将所有细胞分为 6 个细胞类，每个分类的基因表达谱表示为该基因在同类细胞中表达值的中位数，并使用高斯混合模型估计每个分类表达谱的方差。通过严格的分类标准，将具有最小估计方差的细胞类定义为“自信正常的细胞类”，也就是“标准的二倍体细胞集”。

当数据集中只有小部分正常细胞，或肿瘤细胞具有近二倍体基因组并伴有有限拷贝数畸变（Copy number variation，CNV）事件时，可能会发生错误的分类。在这种情况下，CopyKAT 提供了另外一种定义“自信正常”细胞集的方式，称为“GMM”定义模式，以用来逐个识别正常的二倍体细胞。该方法将评估单个细胞的二倍体状态转化为计算每个细胞中“中立拷贝数事件”的比例。具体来说，把经过标准化后的单细胞数据集的每个基因当作变量，假定它们服从三个高斯混合分布，这三个高斯混合分布分别代表拷贝数的三种状态：拷贝数增加、拷贝数中立和拷贝数缺失。相应的高斯分布的初始均值分别定义为 0.2，0，-0.2，初始方差为所有基因表达谱方差的1/2。然后，定义一个新的指标来衡量单个细胞拷贝数是否正常，即单个细胞中属于拷贝数中立事件的基因个数占表达基因个数的比值，表示为

N_{frac} = \frac{{genes}_{abs (mean)} ⩽ 0.05}{N_{genes}},

其中g_enesabs_（_mean_）≤0.05表示均值的绝对值小于0.05 的基因数量，N_genes 表示用于统计的总基因数。如果一个细胞的N_frac≥0.99，那么就认为这个细胞是正常的。将所有正常细胞构成的集合记为“自信正常”细胞集。

正常细胞的拷贝数基线被定义为所有正常细胞各个基因拷贝数的中位数。所有细胞的相对表达值表示为基因表达值减去拷贝数基线值。

4.3 寻找染色体断点

通常，如果在细胞中发生基因拷贝数变异，一些染色体片段所对应的基因数量是异常的，也即跟相邻的正常片段相比较基因的平均表达水平有显著的区别。下面根据这个假设来寻找染色体的断点。

为了找到染色体断点，对于同一个类中的细胞，CopyKAT 首先进行基因窗口分割，然后整合泊松-伽马模型和马尔可夫链的蒙特卡洛（MCMC）迭代生成每个基因窗口的后验均值，最后通过比较相邻基因窗口的后验均值来判定是否出现染色体断点。在 CopyKAT 算法中，先按类寻找染色体断点，然后再把所有细胞类都存在的染色体断点作为全基因组的染色体断点。

在每个细胞类中寻找染色体断点的具体流程如下。首先将相邻的25个基因划分到一个基因窗口（Gene windows）。假设第 k 个类中共有N_k个细胞，则每一个基因就会有N_k个数据。假设基因的表达值 y 服从参数为 λ 的泊松分布，而参数 λ 服从共轭伽马分布，即

\begin{matrix} y \sim P o i s s o n (λ) \\ λ \sim G a m m a (α, β) . \end{matrix}

那么对于每个基因来说，可以利用已知的 N_k个细胞中该基因上的表达值确定参数α，β，从而可以得到参数 λ 的后验分布。然后利用MCMC方法模拟出该基因的 1 000 个模拟值的后验均值 λ^*。将该窗口所有基因的后验均值 λ^*放在一起，作为这个窗口中的基因表达数据。设 F_i（λ^*）为第i个窗口后验均值λ^*的分布。使用KS统计量（Kolmogorov–Smirnov test）评估相邻的两个窗口之间是否有染色体断点。KS 统计量 D 为相邻窗口后验均值的分布函数的差的绝对值最大值，

D = {s u p}_{λ^{*}} |F_{i} (λ^{*}) - F_{j} (λ^{*})|,

其中，λ^*表示窗口i和窗口j相应的后验均值。如果 KS 统计量D大于给定的阈值C₀，就认为窗口i 和窗口 j 的表达值具有显著差异，即窗口i和窗口j之间存在染色体断点。对均值无显著差异的相邻窗口进行合并。如果所有染色体断点的个数小于25，就将阈值变为C₀/2。将各个细胞类之间一致都有的断点作为全体细胞的染色体断点。两个断点之间被认为是一个片段（Segment）。然后，将跨越相邻断点之间所有基因相对表达值的均值作为这个片段的最终拷贝数值。于是，可以通过单细胞转录组数据估计细胞的拷贝数变异谱。

4.4 识别克隆亚群

估计出细胞的拷贝数变异谱后，还需根据拷贝数变异谱识别克隆亚群。首先根据已获得的单细胞拷贝数数据进行细胞分层聚类，确定非整倍体肿瘤细胞与二倍体基质细胞之间的最大距离。如果基因组距离不显著，就切换到“GMM定义模式”，逐个确定单个非二倍体肿瘤细胞。最后，对非二倍体单细胞的拷贝数数据进行聚类，识别不同拷贝数的克隆亚群，并计算出代表亚克隆基因型的共识表达谱，以进一步分析其基因表达差异。

总结上面的流程，CopyKAT 算法结合基因与染色体的关系，首先将单细胞数据集里的基因进行排序并组合在一起，根据同一类细胞的基因表达数据差异较小的假设定义正常细胞集；然后把转录组数据转化为拷贝谱数据；最后根据每个细胞与正常细胞集数据的差异确定该细胞是否发生了拷贝数变异。

5 单细胞转录组数据的非负矩阵分解

单细胞转录组数据集通常以非负的基因表达矩阵形式呈现，表示细胞中基因组表达的数量信息。在数学中，经常使用矩阵分解方法对原始矩阵进行变换，获取潜在的内在结构信息，以进行高维数据的特征提取。近年来，一些学者基于矩阵分解的思想提出了对单细胞转录组数据进行分析的方法^[20-21]，借助非负矩阵分解工具，以新的视角来探索单细胞转录组数据集。这一节介绍单细胞转录组数据非负矩阵分解方法的数学基础和应用。

5.1 矩阵分解

下面先给出矩阵分解的一般形式。对于基因表达矩阵

X = [x_{1}, x_{2}, \dots, x_{n}],

如果可以将大小为 m×n 的矩阵 X 作如下分解

X = W H

(18)

其中

\begin{matrix} W = [w_{1}, w_{2}, \dots, w_{k}], k ⩽ m a x {m, n}, \\ H = {(h_{i j})}_{k \times n}, \end{matrix}

则有

x_{j} = \overset{k}{\underset{i = 1}{Σ}} w_{i} h_{i j}, j = 1, 2, \dots, n .

即矩阵 X 中表示每个细胞的列向量都可以由W矩阵中列向量的线性组合得到，线性组合系数由矩阵 H 中的元素给出。

在上面的分解公式（18）中，通常称W为基矩阵，称H为系数矩阵。这里的基矩阵由 k（

k ≪ n

）个 m 维向量组成，每个向量表示一个特征信息。通过矩阵分解，将原矩阵X的每一个列向量表示成了 W 中k个特征向量的加性线性组合，H 中每一个列向量表示原样本与各个特征样本的相似权重。因此，通过非负矩阵分解可以找到矩阵 X 的特征子结构，即 W 中的所有列向量组成 X 的一组“基底”，从而使用较少的基向量和系数来表示较大的数据矩阵，达到数据降维和特征提取的目的。

5.2 非负矩阵分解

在数学上有各种不同的矩阵分解方法，比如矩阵的三角分解（LU分解）、奇异值分解（SVD分解）和QR分解等。非负矩阵分解（Non-negative matrix factorization，NMF）是一个强大的矩阵分析工具，它的目的是将一个非负矩阵分解为两个非负、低秩的矩阵的乘积，以通过所得到的低秩非负基矩阵提取原矩阵的中有代表性的特征信息^[66]。换句话说，非负矩阵分解能够使我们从原始数据中识别出有意义的和具有代表性的数据模式，将原始样本表示为具有代表性特征的加性线性组合。

非负矩阵分解的目的是对给定的非负矩阵 X≥0，找到两个非负矩阵 W≥0 和 H≥0，使得

X = W H .

而在实际应用中，通常难以实现 X 与 WH完全相等，所以通常只要求X 与 WH 近似相等，并将上诉问题转化为以下优化问题：

\begin{matrix} \underset{W, H}{m i n} ‖ X - W H ‖_{F}^{2} \\ s . t . W, H ⩾ 0 \end{matrix}

(19)

其中

‖ \cdot ‖_{F}

表示 Frobenius 范数，简称为F-范数，定义为矩阵中各项元素的绝对值平方的总和。

在求解最优化问题（19）时，由于目标函数

‖ X - W H ‖_{F}^{2}

只是对变量 W 和 H 之一是凸函数，而不是同时对两个变量的凸函数，因此要想找到全局最优解是很困难的，通常只能通过数值方法求解局部最优解。在常用的最优化方法中，梯度下降算法容易实现，但是收敛速度较慢，而共轭梯度法的收敛速度快，但实现起来比较复杂。基于此，Lee 和 Seung提出基于“乘法更新规则”的优化算法^[66]，交替地对 W 和 H 进行更新。该算法在本质上是梯度下降法，但是需要通过定义特殊的步长和非负初始值来保证迭代过程和结果矩阵 W 和 H 均为非负的。具体的更新规则推导如下面给出。

下面为了推导方便，将目标函数乘以 1/2，而不会改变原问题的最优解。因此，把目标函数记为

\begin{matrix} F (W, H) = \frac{1}{2} ‖ X - W H ‖_{F}^{2} \\ = \frac{1}{2} \underset{i, j}{Σ} {(X_{i j} - (W H)_{i j})}^{2} . \end{matrix}

如果采用梯度下降法求解上述问题，首先需要计算目标函数关于变量 W=（W_il）和 H=（H_lj）的梯度，即

\begin{matrix} \frac{\partial F (W, H)}{\partial W_{i l}} = - \underset{j}{Σ} (X_{i j} - (W H)_{i j}) H_{l j} \\ = - ({(X H^{T})}_{i l} - {(W H H^{T})}_{i l}), \end{matrix}

和

\frac{\partial F (W, H)}{\partial H_{l j}} = - ({(W^{T} X)}_{l j} - {(W^{T} W H)}_{l j}) .

根据所求得的梯度，如果在每一步中采用步长 λ_il 和 μ_lj 对 W_il 和 H_lj 进行更新，则得到如下梯度下降法的更新规则：

\begin{matrix} W_{i l} = W_{i l} + λ_{i l} ({(X H^{T})}_{i l} - {(W H H^{T})}_{i l}), \\ H_{l j} = H_{l j} + μ_{l j} ({(W^{T} X)}_{l j} - {(W^{T} W H)}_{l j}) . \end{matrix}

特别地，为保证每一步的非负性，可以选择合适的步长将负数的部分消除。为此，选取步长

λ_{i l} = \frac{W_{i l}}{{(W H H^{T})}_{i l}}, μ_{l j} = \frac{H_{l j}}{{(W^{T} W H)}_{l j}} .

由此得到乘法更新规则

\begin{matrix} W_{i l} = W_{i l} \frac{{(X H^{T})}_{i l}}{{(W H H^{T})}_{i l}}, i = 1, 2, \dots, m; l = 1, 2, \dots, k, \\ H_{l j} = H_{l j} \frac{{(W^{T} X)}_{l j}}{{(W^{T} W H)}_{l j}}, l = 1, 2, \dots, k; j = 1, 2, \dots, n . \end{matrix}

根据上面的迭代算法，如果选取初始矩阵 W 和 H 为非负矩阵，由上述更新过程可以保证迭代过程及结果的矩阵 W 和H均为非负的。如果该更新算法收敛，则可以得到 X 的非负矩阵分解。

需要注意的是，形如 X=WH 的矩阵分解如果存在的话是不唯一的。例如，对分解 X=WH 和任意非负的可逆矩阵

D \in R^{k \times k}

，都有以下的分解式

X = (W D) (D^{- 1} H),

对应于相同的目标函数值。因此，通常需要额外的约束条件才可以得到唯一的解。对基矩阵 W 或 H 不同的约束，就可以得到不同的矩阵分解方法。例如，可以要求 W是正交的单位向量构成的矩阵，也可以要求 W 是 X 的一个极大线性无关组。在实际应用中，为得到有意义的解，通常需要根据不同数据的特点和需求，引进相应的正则化条件，通过正则化条件的约束获取原始数据的有意义的数据特征。因此，在实际应用非负矩阵分解方法时，关键问题是如何提出合适的正则化条件。而对于不同形式的正则化条件，如何保证解的唯一性仍然是有待解决的重要数学问题。

非负矩阵分解方法被提出以后引起了广泛关注^[73]，许多由矩阵来描述的数据集都可以通过非负矩阵分解方法来获得有趣的数据模式。例如，图像在计算机中可以以矩阵的形式进行存放，针对图像的识别、分析和处理也是在矩阵的基础上进行操作的。基于矩阵表示，非负矩阵分解方法能够很好地与图像分析和处理结合起来，例如在人脸识别等问题中起重要作用。除了在图像分析中的应用外，非负矩阵分解还被用于话题识别、语音处理、降维、聚类、机器人控制、生物医学工程中的数据处理^[74]等。

非负矩阵分解方法与主成分分析不同，主成分分析对于数据特征的处理是找到特征重建的最佳方向，而非负矩阵分解通常并不应用于对数据进行重建或者编码，而是寻找数据中的有趣模式和结构特征。非负矩阵分解方法适合于分解具有叠加结构的数据，包括图像、音频、基因表达和文本数据等。

5.3 单细胞转录组数据的非负矩阵分解

在单细胞转录组数据分析中经常需要回答以下两个问题：组织中有哪些细胞类型？每个细胞类型的表达模式如何确定？通过非负矩阵分解对基因表达矩阵进行特征提取很适合回答这两个问题。根据矩阵分解所得到的因子可以直接对应于细胞类型或基因表达模式，具有很好的生物学解释。在单细胞转录组数据的非负矩阵分解研究中，通过引进不同的约束条件可以得到不同的结果，分别对应于不同的生物学含义。基于非负矩阵分解的单细胞转录组数据分析，与传统数据分析的视角不一样，它基于样本数据和目标函数学习新的特征表示。针对所要探索的科学问题，可以设置不同的约束条件。因此，基于非负矩阵分解的方法为数据探索提供了新的研究范式。

在这里以具体的基于单细胞随机约束的非负矩阵分解算法（scRCMF）^[21]来介绍非负矩阵分解在单细胞转录组数据分析中的应用。scRCMF方法将一个随机约束项加在非负矩阵分解算法中，以通过基矩阵识别细胞亚群。同时，为了在单细胞数据分析中识别细胞亚群和过渡状态的细胞，scRCMF 根据矩阵分解的结果定义了一个用来量化转移能力的度量，即单细胞转移熵。

scRCMF算法的输入为基因表达矩阵 X=（x_ij），其中 x_ij表示第 i个基因在第 j 个细胞中的表达量。该算法主要由3个关键步骤组成：

1）基于非负矩阵分解的非线性优化模型学习低秩的基矩阵和系数矩阵；

2）利用基矩阵和系数矩阵识别细胞亚群和转移状态细胞，同时得到不同亚群的特征基因；

3）定义单细胞转移熵，对处于转移状态细胞的转移能力进行量化。

下面详细介绍这3个步骤的计算过程。

首先，通过非线性优化模型提取低秩结构。为了从单细胞数据集中揭示子结构，scRCMF 根据预先设定的细胞类数 k 将单细胞基因表达矩阵

X \in R^{m \times n}

分解为两个低秩的非负矩阵

W \in R^{m \times k}

和

H \in R^{k \times n}

，然后根据低秩矩阵识别细胞类型。

为对基因表达矩阵进行非负矩阵分解，可以求解下面的非线性优化模型

\underset{W ⩾ 0, H ⩾ 0}{m i n} F (W, H, k) = ‖ X - W H ‖_{F} + λ ‖ I - R H ‖_{F}

(20)

其中

W \in R^{m \times k}

为基矩阵，

H \in R^{k \times n}

为系数矩阵，m，n 分别表示基因数和细胞的个数，k 表示细胞亚群的个数，λ 是正则化参数，I 表示 n 阶的单位矩阵，

R \in R^{n \times k}

是随机矩阵，其分量R_ij∈[0，1]。这里的正则化项

λ ‖ I - R H ‖_{F}

和随机约束矩阵 R 的引进是为了保证非负矩阵分解的鲁棒性和非病态性，并通过调整 λ 来平衡子结构结果的稳定性和精确性的。可以使用Gap 统计量来确定类的数量k。而对于正则化参数 λ 的确定，可以使用 BIC 准则从 λ=0.001，0.01，0.1，1，10 中挑选参数 λ。

下面介绍如何通过基矩阵和系数矩阵识别细胞亚群和转移状态的细胞。在优化模型公式（20）中，基于推断得到的细胞类数k 将基因表达矩阵 X 分解为低秩的结构以探索基因或细胞的子结构。一般地，系数矩阵中每一列的最大值可以用来决定相应的细胞是属于哪一个类的。按照这一思路，每一个细胞都可以被唯一地标记出它所属的子类。然而有一些细胞可以处于中间状态，也就是说一个细胞可能有多个身份，介于两个或多个亚群之间。为了确定这些处于转移状态的细胞，将系数矩阵的每一列作标准化处理，将每一列的和归一化为 1，即得到由下式所定义的概率矩阵

P \in R^{k \times n}

P_{i j} = \frac{H_{i j}}{\overset{k}{\underset{i = 1}{Σ}} H_{i j}}

(21)

标准化处理以后的概率矩阵的元素P_ij 表示第j 个细胞属于第i 类的概率。下面通过概率矩阵 P 来确定各个细胞的类型和处于转移状态的细胞。直观地说，如果P_ij 是在第 j 列中最大的元素，并且大于给定的阈值C₀，那么细胞 j 就可以被唯一地分配到类型i 中。否则，如果细胞j 属于各个类的概率值都小于C₀，即

P_{s j} < C_{0}, s = 1, 2, \dots, k,

则表示这个细胞被等概率地分配到各个类中。这种无法确定细胞类型的细胞就被认为是转移细胞。例如，对于仅考虑两种转移状态细胞的情况，将处于 u，v 两种转移状态的细胞定义如下：

\begin{matrix} T C_{u, v} = \{j ∣ C_{0} > P_{u j} > P_{v j} > P_{l j}, l \neq u \neq v, \\ 1 ⩽ l ⩽ k}, \end{matrix}

即对细胞j，u 和v是所有概率P_ij（i=1，2，···，k）中两个最大值的类指标。由上面的定义可以看到，概率矩阵 P 提供了一种自然的方式来确定转移细胞。

基矩阵 H 提供了一个无偏、直接的方式去挑选每个类的特征基因。在数学上，细胞类 C_i和它的相关基因 G_i可以如下定义：

\begin{matrix} C_{i} = \{j ∣ P_{i j} ⩾ P_{s j} ⩾ C_{0}, i \neq s, s = 1, \dots, k\}, \\ G_{i} = \{l ∣ W_{l i} ⩾ W_{l j}, j \neq i, j = 1, \dots, k\}, \end{matrix}

其中，C₀是概率阈值，通常大于1/k，其中 k 是细胞类型的个数。由这一方法所得到的细胞类型分类结果对C₀ 的选取并不敏感。这里 G_i 给出了类i的特征基因的指标。对于转移细胞类型 u 和 v，可以定义转移基因为在转移细胞中表达值大于平均基因表达值的基因。

最后，根据上面的结果来计算量化细胞可塑性的单细胞转移熵。为了量化表示细胞的可塑性，可以通过概率矩阵按以下公式定义单细胞转移熵（scTE）来表示细胞类型不确定性的指标：

E_{j} = - \overset{k}{\underset{i = 1}{Σ}} P_{i j} l o g (P_{i j})

(22)

单细胞转移熵通过细胞转移概率所定义的熵表示一个细胞的命运不确定程度，即转移细胞通常表现出比稳定细胞更高的转移熵。

这里所介绍的单细胞转录组数据集的非负矩阵分解所得到的基矩阵和系数矩阵具有生物学上的可解释性，巧妙地将数学工具与数据信息结合起来，通过系数矩阵得到“伪概率”，并可以根据“伪概率”计算出细胞的转移熵，用于衡量转移细胞状态的不确定性。因此可以看到，非负矩阵分解是从数据集中获取潜在信息的一种有力工具，通过对基矩阵进行约束，可以对数据集实现不同程度的降维。scRCMF算法对系数矩阵进行聚类，比 k-均值聚类、KNN聚类等算法更具有可解释性，不仅对细胞类型和转移细胞进行了划分，还通过分解所得到的基矩阵获得各类细胞的标记基因，所得到的结果具有很好的说服力和可解释性。

6 总结与展望

本文围绕单细胞转录组数据分析的一般流程，介绍数据分析过程所涉及到的数学基础，包括矩阵分析、图论、最优化方法和统计相关知识等。通过对数据分析的数学基础的介绍，更加清楚地展现单细胞转录组数据分析的理论依据和各种方法的优缺点，有利于进一步发展和应用各种数据分析方法。同时，通过对数学基础的了解，也促进根据实际问题和需求开发新的数据分析方法，发展单细胞转录组数据可解释性的数据分析和特征提取方法。

近年来，针对单细胞转录组数据分析的研究工作发展很快，有很多新的方法和研究结果被发表。这些数据分析方式所涉及的数学知识基础也必然会越来越多。本综述文章仅仅对作者所感兴趣的一些方法进行介绍，必然无法覆盖所有相关的知识。例如，近年来有一些工作采用最优传输理论和张量分析等方法进行单细胞数据分析^[75-78]，根据单细胞测序数据分析细胞间通讯关系，例如细胞通讯分析工具CellPhoneDB^[79]，CellChat^[80]和 iTALK^[81]等。这些内容相关的数学基础在这里并没有涉及。在对单细胞转录组数据的分析中，除了细胞的聚类和新细胞类型识别等问题外，如何通过单细胞转录组数据推断基因调控网络，如何定量刻画肿瘤的免疫微环境和如何确定细胞间的通讯关系等，都是既有意义又有挑战的研究课题。对这些问题的研究需要综合运用矩阵分析的数学工具并结合生物学知识进行综合研究，有时还需要根据实际需要建立新的数学方法。

此外，近年来单细胞空间转录组的数据分析已经成为研究的热点领域^[82-83]，相关的数据分析方法除了需要考虑基因表达矩阵外，还需要考虑细胞的空间位置等，所采用数据分析方法还在不断发展中，这里暂时没有涉及相关的内容。

图1基因表达矩阵

Fig.1Gene expression matrix

下载: 全尺寸图片

图2数据预处理

Fig.2Data preprocessing

下载: 全尺寸图片

图3单细胞数据集的特征

Fig.3scRNA-seq dataset's feature

下载: 全尺寸图片

图4主成分分析（PCA）示意图

Fig.4Schematic diagram of PCA

下载: 全尺寸图片

图5数据集 pbmc3k 两个主成分的投影

Fig.5Principal components projection of the dataset pbmc3k

下载: 全尺寸图片

图6数据集 pbmc3k 的数据可视化

Fig.6Visualization of pbmc3k dataset

下载: 全尺寸图片

图7模块度计算示例

Fig.7Example of module degree calculation

下载: 全尺寸图片

图8CopyKAT 的工作流程

Fig.8Workflow of CopyKAT

下载: 全尺寸图片

图1基因表达矩阵

Fig.1Gene expression matrix

图2数据预处理

Fig.2Data preprocessing

图3单细胞数据集的特征

Fig.3scRNA-seq dataset's feature

图4主成分分析（PCA）示意图

Fig.4Schematic diagram of PCA

图5数据集 pbmc3k 两个主成分的投影

Fig.5Principal components projection of the dataset pbmc3k

图6数据集 pbmc3k 的数据可视化

Fig.6Visualization of pbmc3k dataset

图7模块度计算示例

Fig.7Example of module degree calculation

图8CopyKAT 的工作流程

Fig.8Workflow of CopyKAT

引用提醒

图(8)

引用本文

罗琴琴,雷锦志.单细胞转录组数据分析中的数学[J].生物信息学，2025,23(1):1-27.

复制

LUO Qinqin, LEI Jinzhi.Mathematics in single-cell RNA transcriptome analysis[J].Chinese Journal of Bioinformatics，2025,23(1):1-27.

Copy

计量

图1基因表达矩阵

Fig.1Gene expression matrix

图2数据预处理

Fig.2Data preprocessing

图3单细胞数据集的特征

Fig.3scRNA-seq dataset's feature

图4主成分分析（PCA）示意图

Fig.4Schematic diagram of PCA

图5数据集 pbmc3k 两个主成分的投影

Fig.5Principal components projection of the dataset pbmc3k

图6数据集 pbmc3k 的数据可视化

Fig.6Visualization of pbmc3k dataset

图7模块度计算示例

Fig.7Example of module degree calculation

图8CopyKAT 的工作流程

Fig.8Workflow of CopyKAT

TANG Fuchou, BARBACIORU C, WANG Yangzhou,et al.mRNA-Seq whole-transcriptome analysis of a single cell[J]. Nature Methods,2009,6(5):377-382. DOI:10.1038/nmeth.1315.

SVENSSON V, VENTO-TORMO R, TEICHMANN S A,et al. Exponential scaling of single-cell RNA-seq in the past decade[J]. Nature Protocols,2018,13(4):599-604. DOI:10.1038/nprot.2017.149.

REN Xianwen, ZHANG Lei, ZHANG Yuanyuan,et al. Insights gained from single-cell analysis of immune cells in the tumor microenvironment[J]. Annual Review of Immunology,2021,39:583-609. DOI:10.1146/annurev-immunol-110519-071134.

GUO Guoji, HUSS M, TONG Guoqing,et al. Resolution of cell fate decisions revealed by single-cell gene expression analysis from zygote to blastocyst[J]. Developmental Cell,2010,18(4):675-685. DOI:10.1016/j.devcel.2010.02.012.

QIU Xiaojie, ZHANG Yan, MARTIN-RUFINO J D,et al. Mapping transcriptomic vector fields of single cells[J]. Cell,2022,185(4):690-711.e45. DOI:10.1016/j.cell.2021.12.045.

CHEN Zhaohui, ZHOU Lijie, LIU Lihong,et al. Single-cell RNA sequencing highlights the role of inflammatory cancer-associated fibroblasts in bladder urothelial carcinoma[J]. Nature Communications,2020,11(1):1-12. DOI:10.1038/s41467-020-18916-5.

CHENG Sijin, LI Ziyi, GAO Ranran,et al. A pan-cancer single-cell transcriptional atlas of tumor infiltrating myeloid cells[J]. Cell,2021,184(3):792-809.e23. DOI:10.1016/j.cell.2021.01.010.

GUO Xinyi, ZHANG Yuanyuan, ZHENG Liangtao,et al. Global characterization of T cells in non-small-cell lung cancer by single-cell sequencing[J]. Nature Medicine,2018,24(7):978-985. DOI:10.1038/s41591-018-0045-3.

ZHANG Qiming, HE Yao, LUO Nan,et al. Landscape and dynamics of single immune cells in hepatocellular carcinoma[J]. Cell,2019,179(4):829-845. DOI:10.1016/j.cell.2019.10.003.

ZHANG Lei, YU Xin, ZHENG Liangtao,et al. Lineage tracking reveals dynamic relationships of T cells in colorectal cancer[J]. Nature,2018,564(7735):268-272. DOI:10.1038/s41586-018-0694-x.

LIU Baolin, HU Xueda, FENG Kaichao,et al. Temporal single-cell tracing reveals clonal revival and expansion of precursor exhausted T cells during anti-PD-1 therapy in lung cancer[J]. Nature Cancer,2022,3(1):108-121. DOI:10.1038/s43018-021-00292-8.

GUO Chuang, LI Bin, MA Huan,et al.single-cell analysis of two severe COVID-19 patients reveals a monocyte-associated and tocilizumab-responding cytokine storm[J]. Nature Communications,2020,11(1):1-11. DOI:10.1038/s41467-020-17834-w.

LEADER A M, GROUT J A, MAIER B B,et al.single-cell analysis of human non-small cell lung cancer lesions refines tumor classification and patient stratification[J]. Cancer Cell,2021,39(12):1595-1609. DOI:10.1016/j.ccell.2021.10.009.

CHENG Sijin, LI Ziyi, GAO Ranran,et al. A pan-cancer single-cell transcriptional atlas of tumor infiltrating myeloid cells[J]. Cell,2021,184(3):792-809. DOI:10.1016/j.cell.2021.01.010.

PURAM SV, TIROSH I, PARIKH A S,et al.single-cell transcriptomic analysis of primary and metastatic tumor ecosystems in head and neck cancer[J]. Cell,2017,171(7):1611-1624. DOI:10.1016/j.cell.2017.10.044.

ZHENG Liangtao, QIN Shishang, SI Wen,et al. Pan-cancer single-cell landscape of tumor-infiltrating T cells[J]. Science,2021,374(6574):64-74. DOI:10.1126/science.abe6474.

LAFZI A, MOUTINHO C, PICELLI S,et al. Tutorial: Guidelines for the experimental design of single-cell RNA sequencing studies[J]. Nature Protocols,2018,13(12):2742-2757. DOI:10.1038/s41596-018-0073-y.

WANG Bo, ZHU Junjie, PIERSON E,et al. Visualization and analysis of single-cell RNA-seq data by kernel-based similarity learning[J]. Nature Methods,2017,14(4):414-416. DOI:10.1038/nmeth.4207.

BUTLER A, HOFFMAN P, SMIBERT P,et al. Integrating single-cell transcriptomic data across different conditions,technologies,and species[J]. Nature Biotechnology,2018,36(5):411-420. DOI:10.1038/nbt.4096.

WANG Shuxiong, KARIKOMI M, MACLEAN A L,et al. Cell lineage and communication network inference via optimization for single-cell transcriptomics[J]. Nucleic Acids Research,2019,47(11):e66-e66. DOI:10.1093/nar/gkz204.

ZHENG Xiaoying, JIN Suoqin, NIE Qing,et al.scRCMF: Identification of cell subpopulations and transition states from Single-Cell transcriptomes[J]. IEEE Transactions on Biomedical Engineering,2019,67(5):1418-1428. DOI:10.1109/TBME.2019.2937228.

KISELEV V Y, KIRSCHNER K, SCHAUB M T,et al. SC3: Consensus clustering of single-cell RNA-seq data[J]. Nature Methods,2017,14(5):483-486. DOI:10.1038/nmeth.4236.

KISELEV V Y, ANDREWS T S, HEMBERG M. Challenges in unsupervised clustering of single-cell RNA-seq data[J]. Nature Reviews Genetics,2019,20(5):273-282. DOI:10.1038/s41576-018-0088-9.

KESTER L, VAN OUDENNAARDEN A. Single-cell transcriptomics meets lineage tracing[J]. Cell Stem Cell,2018,23(2):166-179. DOI:10.1016/j.stem.2018.04.014.

CANNOODT R, SAELENS W, SAEYS Y. Computational methods for trajectory inference from single-cell transcriptomics[J]. European Journal of Immunology,2016,46(11):2496-2506. DOI:10.1002/eji.201646347.

WELCH J D, HARTEMINK A J, PRINS J F. SLICER: Inferring branched,nonlinear cellular trajectories from single cell RNA-seq data[J]. Genome Biology,2016,17(1):1-15. DOI:10.1186/s13059-016-0975-3.

HERRING C A, BANERJEE A, MCKINLEY E T,et al. Unsupervised trajectory analysis of single-cell RNA-seq and imaging data reveals alternative tuft cell origins in the gut[J]. Cell Systems,2018,6(1):37-51. DOI:10.1016/j.cels.2017.10.012.

QIU Xiaojie, MAO Qi, TANG Ying,et al. Reversed graph embedding resolves complex single-cell trajectories[J]. Nature Methods,2017,14(10):979-982. DOI:10.1038/nmeth.4402.

HAGHVERDI L, BUETTNER F, THEIS F J,et al. Diffusion maps for high-dimensional single-cell analysis of differentiation data[J]. Bioinformatics,2015,31(18):2989-2998. DOI:10.1093/bioinformatics/btv325.

HAGHVERDI L, BUETTNER M, WOLF F A,et al. Diffusion pseudotime robustly reconstructs lineage branching[J]. Nature Methods,2016,13(10):845-848. DOI:10.1038/nmeth.3971.

JI Zhicheng, JI Hongkai. TSCAN: Pseudo-time reconstruction and evaluation in single-cell RNA-seq analysis[J]. Nucleic Acids Research,2016,44(13):e117-e117. DOI:10.1093/nar/gkw430.

SHIN J, BERG D A, ZHU Yunhua,et al. Single-cell RNA-seq with waterfall reveals molecular cascades underlying adult neurogenesis[J]. Cell Stem Cell,2015,17(3):360-372. DOI:10.1016/j.stem.2015.07.013.

SETTY M, TADMOR M D, ANGEL O,et al. Wishbone identifies bifurcating developmental trajectories from single-cell data[J]. Nature Biotechnology,2016,34(6):637-645. DOI:10.1038/nbt.3569.

BENDALL S C, DAVIS K L, TADMOR M D,et al. Single-cell trajectory detection uncovers progression and regulatory coordination in human B cell development[J]. Cell,2014,157(3):714-725. DOI:10.1016/j.cell.2014.04.005.

CHEN Jinmiao, SCHLITZER A, CHAKAROV S,et al. Mpath maps multi-branching single-cell trajectories revealing progenitor cell progression during development[J]. Nature Communications,2016,7:11988. DOI:10.1038/ncomms11988.

RASHID S, KOTTON D N, BAR-JOSEPH Z. TASIC: Determining branching models from time series single cell data[J]. Bioinformatics,2017,33(16):2504-2512. DOI:10.1093/bioinformatics/btx173.

TESCHENDORFF A E, ENVER T. Single-cell entropy for accurate estimation of differentiation potency from a cell's transcriptome[J]. Nature Communications,2017,8:15599. DOI:10.1038/ncomms15599.

JIN Suoqin, MACLEAN A L, PENG Tao,et al.scEpath: Energy landscape-based inference of transition probabilities and cellular trajectories from single-cell transcriptomic data[J]. Bioinformatics,2018,34(12):2077-2086. DOI:10.1093/bioinformatics/bty058.

LAFZI A, MOUTINHO C, PICELLI S,et al. Tutorial: Guidelines for the experimental design of single-cell RNA sequencing studies[J]. Nature Protocols,2018,13(12):2742-2757. DOI:10.1038/s41596-018-0073-y.

XU Qianhui, CHEN Shaohuai, HU Yuanbo,et al. Single-cell RNA transcriptome reveals the intra-tumoral heterogeneity and regulators underlying tumor progression in metastatic pancreatic ductal adenocarcinoma[J]. Cell Death Discovery,2021,7(1):331. DOI:10.1038/s41420-021-00663-1.

ALJANAHI A A, DANIELSEN M, DUNBAR C E. An Introduction to the Analysis of single-cell RNA-Sequencing Data[J]. Molecular Therapy Methods & Clinical Development,2018,10:189-196. DOI:10.1016/j.omtm.2018.07.003.

LOVE M I, HUBER W, ANDERS S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2[J]. Genome Biology,2014,15(12):550. DOI:10.1186/s13059-014-0550-8.

TANG Wenhao, BERTAUX F, THOMAS P,et al.bayNorm: Bayesian gene expression recovery,imputation and normalization for single-cell RNA-sequencing data[J]. Bioinformatics,2020,36(4):1174-1181. DOI:10.1093/bioinformatics/btz726.

LAURENS V M, GEOFFREY H. Visualizing data using t-SNE[J]. Journal of Machine Learning Research,2008,9(86):2579-2605. DOI:10.1.1.457.7213.

MCINNES L, HEALY J. UMAP: Uniform manifold approximation and projection for dimension reduction[J].the Journal of Open Source Software,2018,3(29):861. DOI:10.21105/joss.00861.

HAGHVERDI L, LUN A T L, MORGAN M D,et al. Batch effects in single-cell RNA-sequencing data are corrected by matching mutual nearest neighbors[J]. Nature Biotechnology,2018,36(5):421-427. DOI:10.1038/nbt.4091.

LIN C, JAIN S, KIM H,et al. Using neural networks for reducing the dimensions of single-cell RNA-Seq data[J]. Nucleic Acids Research,2017,45(17):e156. DOI:10.1093/nar/gkx681.

CHO H, BERGER B, PENG Jian. Generalizable and scalable visualization of single-cell data using neural networks[J]. Cell Systems,2018,7(2):185-191. DOI:10.1016/j.cels.2018.05.017.

AIBAR S, GONZALEZ-BLAS C B, MOERMAN T,et al. SCENIC: Single-cell regulatory network inference and clustering[J]. Nature Methods,2017,114(11):1083-1086. DOI:10.1038/nmeth.4463.

JOHN A H, MANCHEK A W. Algorithm AS 136: A k-means clustering algorithm[J]. Journal of the Royal Statistical Society,1979,28(1):100-108. DOI:10.2307/2346830.

LUECKEN M D, THEIS F J. Current best practices in single-cell RNA-seq analysis: A tutorial[J]. Molecular Systems Biology,2019,15(6):e8746. DOI:10.15252/msb.20188746.

WOLF F A, ANGERER P, THIEIS F J. SCANPY: Large-scale single-cell gene expression data analysis[J]. Genome Biology,2018,19:15. DOI:10.1186/s13059-017-1382-0.

YANG Lu, LIU Jiancheng, LU Qiang,et al. SAIC: An iterative clustering approach for analysis of single cell RNA-seq data[J]. BMC Genomics,2017,18:689. DOI:10.1186/s12864-017-4019-5.

ŽURAUSKIENÈ J, YAU C.pcaReduce: Hierarchical clustering of single cell transcriptional profiles[J]. BMC Bioinformatics,2016,17:140. DOI:10.1186/s12859-016-0984-y.

GRUN D, LYUBIMOVA A, KESTER L,et al. Single-cell messenger RNA sequencing reveals rare intestinal cell types[J]. Nature,2015,525:251. DOI:10.1038/nature14966.

GRUN D, MURARO M J, LYUBIMOVA A,et al. De novo prediction of stem cell identity using single-cell transcriptome data[J]. Cell Stem Cell,2016,19:266. DOI:10.1016/j.stem.2016.05.010.

HERMAN J S, GRUN D. FateID infers cell fate bias in multipotent progenitors from single-cell RNA-seq data[J]. Nature Methods,2018,15:379. DOI:10.1038/nmeth.4662.

李航. 统计学习方法[M]. 北京: 清华大学出版社,2012,261-263. LI Hang. Statistic learning method[M]. Beijing: Tsinghua University Press,2012,261-263.

LIN Peijie, TROUP M, HO J W K. CIDR: Ultrafast and accurate clustering through imputation for single-cell RNA-seq data[J]. Genome Biology,2017,18:59. DOI:10.1186/s13059-017-1188-0.

ZEISEL A, CODELUPPI S, LA MANNO G,et al. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq[J]. Science,2015,347:1138. DOI:10.1126/science.aaa1934.

GUO Minzhe, WANG Hui, POTTER S S,et al. SINCERA: A pipeline for single-cell RNA-seq profiling analysis[J]. PLoS Computational Biology,2015,11:e1004575. DOI:10.1371/journal.pcbi.1004575.

LUXBURG U V. A tutorial on spectral clustering[J]. Statistics and Computing,2007,17(4):395-416. DOI:10.1007/s11222-007-9033-z.

BLONDEL V D, LAMBIOTTE R, LEFEBVRE E,et al. Fast unfolding of communities in large networks[J] Journal of Statistical Mechanics: Theory and Experiment,2008,2008: P10008. DOI:10.1088/1742-5468/2008/10/P10008.

DEPASQUALE E A K, SCHNELL D J, VAN CAMP P J,et al. DoubletDecon: Deconvoluting doublets from single-cell RNA-sequencing data[J]. Cell Reports,2019,29(6):1718-1727.e8. DOI:10.1016/j.celrep.2019.09.082.

WOLOCK S L, LOPEZ R, KLEIN A M. Scrublet: Computational identification of cell doublet s in single-cell transcriptomic data[J]. Cell Systems,2019,8(4):281-291.e9. DOI:10.1016/j.cels.2018.11.005.

MCGINNIS C S, MURROW L M, Gartner Z J. Doublet finder: Doublet detection in single-cell RNA sequencing data using artificial nearest neighbors[J]. Cell Systems,2019,8(4):329-337.e4. DOI:10.1016/j.cels.2019.03.003.

TRAPNELL C, CACCHIARELLI D, GRIMSBY J,et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells[J]. Nature Biotechnology,2014,32(4):381-386. DOI:10.1038/nbt.2859.

CAO Junjie, SPIELMANN M, QIU Xiaojie,et al. The single-cell transcriptional landscape of mammalian organogenesis[J]. Nature,2019,566(7745):496-502. DOI:10.1038/s41586-019-0969-x.

WOLF F A, HAMEY F, PLASS M,et al. PAGA: Graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells[J]. Genome Biology,2019,20:1-9. DOI:10.1101/208819.

YAN W, WU W. Data Structure[M].2nd ed. Beijing: Tsinghua University Press,1992,168-174.

GAO Ruli, BAI Shanshan, LIN Y,et al. Delineating copy number and clonal substructure in human tumors from single-cell transcriptomes[J]. Nature Biotechnology,2021,39(5):599-608. DOI:10.1038/s41587-020-00795-2.

BERRY M W, BROWNE M, LANGVILLE A N,et al. Algorithms and applications for approximate nonnegative matrix factorization[J]. Computational Statistics & Data Analysis,2007,52(1):155-173. DOI:10.1016/j.csda.2006.11.006.

LI Xinyu, AN Hongbang, ZHANG Luyu,et al. Non-negative matrix factorization model-based construction for molecular clustering and prognostic assessment of head and neck squamous carcinoma[J]. Heliyon,2022,8(8):e10100. DOI:10.1016/j.heliyon.2022.e10100.

NI Zhijie, ZHENG Xiaoying, ZHENG Xiao,et al.scLRTD: A novel low rank tensor decomposition method for imputing missing values in single-cell multi-omics sequencing data[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics,2022,19(2):1144-1153. DOI:10.1109/TCBB.2020.3025804.

WANG Ruohan, Wang Jianping, LI Shuaicheng. Probabilistic tensor decomposition extracts better latent embedding from single-cell multiomic data[J]. Nucleic Acids Research,2023,51(15):e81. DOI:10.1093/nar/gkad570.

SCHIEBINGER G, SHU Jian, TABAKA M,et al. Optimal-transport analysis of single-cell gene expression identifies development trajectories in reprogramming[J]. Cell,2019,176(4):928-943.e22. DOI:10.1016/j.cell.2019.01.006.

ZHANG S, AFANASSIEV A, GREENSTREET L,et al. Optimal transport analysis reveals trajectories in steady-state systems[J]. PLoS Computational Biology,2021,17(12):e1009466. DOI:10.1371/journal.pcbi.1009466.

EFREMOVA M, VENTO-TORMO M, TEICHMANN S A,et al. CellPhoneDB: Inferring cell-cell communication from combined expression of multi-subunit ligand-receptor complexes[J]. Nature Protocols,2020,15(4):1484-1506. DOI:10.1038/s41596-020-0292-x.

JIN Suoqin, JUAREZ C F G, ZHANG Lihua,et al. Inference and analysis of cell-cell communication using CellChat[J]. Nature Communications,2021,12:1088. DOI:10.1038/s41467-021-21246-9.

WANG Yuanxin, WANG Ruiping, ZHAO Shaojun,et al.iTALK: An R package to characterize and illustrate intercellular Communication[EB/OL].(2019-01-04).https://doi.org/10.1101/507871. BioRxiv,2019. DOI:10.1101/507871.

MOSES L, PACHTER L. Museum of spatial transcriptomics[J]. Nature Methods,2022,19(5):534-546. DOI:10.1038/s41592-022-01409-2.

LEE H J, ASATSUMA T, HAQUE A,et al. An introduction to spatial transcriptomics for biomedical research[J]. Genome Medicine,2022,14(1):68. DOI:10.1186/s13073-022-01075-1.

1 数据描述

2 数据预处理

3 聚类分析

4 基因拷贝数变异分析

5 单细胞转录组数据的非负矩阵分解

6 总结与展望

友情链接LINKS