单细胞测序技术能够对单个细胞的基因组、转录组、蛋白组和代谢组进行测量[1],进而揭示细胞类型、罕见亚型、功能状态以及发育轨迹等信息,为疾病诊断、治疗和预防提供更有效的方法和手段。单细胞测序技术还能探索肿瘤内部的异质性和细胞微环境,揭示免疫细胞在不同病理状态下的分子机制和亚群特征,开发更有效的免疫治疗策略[2]。
空间转录组学技术可以在揭示组织或细胞基因表达谱的同时,保留细胞的空间位置信息[3]。通过对基因表达谱进行高分辨率检测并保留测序细胞的空间坐标,有助于探索基因表达的时空动态变化,从而更好地理解细胞功能和组织结构、研究细胞和组织的异质性、探明疾病的发生机理和进展过程[4]。目前,国内外已有多种空间转录技术,如Slide-seqV2[5], LCM-seq[6], Stereo-seq[7]以及10x Visium[8]。
细胞亚群聚类和空间域识别是空间转录组学数据分析的关键。空间域识别和细胞亚群聚类指将空间位置信息与基因表达谱数据相结合,鉴定不同生理状态下具有类似表达模式的细胞,推断细胞类型及其相互作用方式[9]。基于识别的空间区域和细胞亚群,能够开展刻画基因表达模式和基因增补,空间位点去卷积,细胞空间位置重构,细胞通讯和基因交互等研究。
目前,国内外学者开展了一系列空间转录组细胞亚群聚类和空间域识别的研究。如纽约大学基因组学与系统生物学中心发布基于R语言的Seurat工具箱[10],将单细胞测序和空间转录组学数据分析流程化,包含质控、细胞筛选、细胞类型鉴定、特征基因选择、差异表达分析、数据可视化等功能。德国环境健康研究中心计算生物学研究所发布基于Python的Scanpy和Squidpy工具箱[11-12],构建了在Python中单细胞测序和空间转录组学数据分析生态环境,包含了数据预处理、可视化、聚类、伪时间分析,轨迹推断和差异表达分析等手段。在Seurat和Scanpy中,主要细胞亚群聚类和空间域识别的方法是K-means[13]和Leiden[14],它们都是传统的聚类算法。mclust[15]是利用R语言编写的基于高斯混合模型的聚类方法,在处理具有不同分布的数据时,具有很好的效果。隐马尔可夫随机场[16](Hidden markov random field,HMRF)模型能够有效地描述细胞空间位置上下文信息,通过构建能量函数来实现细胞类型识别。全贝叶斯统计模型[17](Fully bayesian statistical model)定义基于最大似然估计的聚类优化目标函数,根据细胞亚群划分间的加权似然进行聚类。然而,上述聚类方法只考虑了细胞基因表达谱信息,并没有兼顾空间位置信息,导致空间域识别和细胞亚群聚类的结果精度并不高。
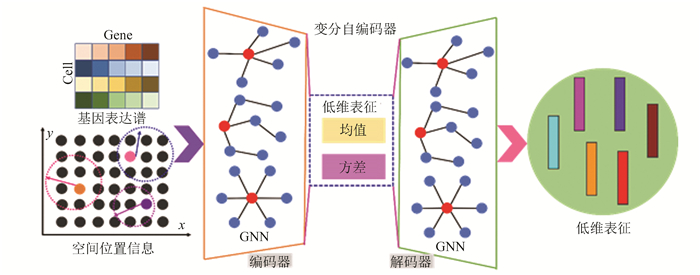
近两年,图深度学习被认为是分析空间转录组学数据的有效方法[18]。图神经网络能充分利用空间转录组数据中的细胞基因表达谱和空间位置信息,因此它是提升空间转录组细胞亚群聚类精度的强力手段。本文提出基于变分自编码器和图神经网络的细胞亚群聚类方法,如图 1所示。通过基因表达谱筛选高度可变基因,组成特征矩阵;利用空间位置信息计算欧式距离,形成邻接矩阵。特征矩阵和邻接矩阵经变分自编码器处理,生成低维表征,下游聚类方法对低维表征进行分类,得到不同细胞亚群。其中,变分自编码器由编码器和解码器组成,均是双层结构,每一层包含简化图卷积(Simple graph convolution, SGC),用以生成低维表征。在常用空间转录数据集上,将提出的分类方法与多个基准方法进行比较,证明其具有更好的聚类准确性。
|
图 1 基于变分自编码器的空间转录组细胞亚群聚类架构 Figure 1 Cell clustering architecture for spatial transcriptomics based on variational autoencoder |
在细胞亚群聚类任务中,变分自编码器(VGAE)的输入是由基因表达谱生成的特征矩阵X和由空间位置信息计算得到的邻接矩阵A。变分自编码器的关键点是应用双层图神经网络结构来生成低维表征。第一层图神经网络用以计算一个低维特征矩阵
| $ {\mathop X\limits^ \circ}=G N N(X, A)=\operatorname{Re} L U\left({\mathop A\limits^ \circ} X W_0\right) \\ {\mathop A\limits^ \circ}=D^{-\frac{1}{2}} A D^{-\frac{1}{2}} $ | (1) |
其中,
在第二层图神经网络中,使用权重参数W1计算特征矩阵的均值和方差向量:
| $ \begin{align*} & \mu=G N N_{\mu}(X, A)=\mathop A\limits^ \circ \mathop X\limits^ \circ W_{1}\\ & \log \sigma^{2}=G N N_{\sigma}(X, A)=\mathop A\limits^ \circ \mathop X\limits^ \circ W_{1} \end{align*} $ | (2) |
其中,均值和方差共享同一类权重系数。在此基础上,利用重参数化方法[19]来计算得到低维表征:
| $ \mathrm{Z}=\mu+\sigma e \varepsilon $ | (3) |
| $ p(A \mid Z)=\sigma\left(Z \cdot Z^{T}\right) $ | (4) |
最后,损失函数包含两种类型的误差。第一类是重构误差,用于衡量输入和输出邻接矩阵之间的相似性。第二类误差使初始标签q和预测标签p尽可能接近。损失函数的数学表达式为
| $ \begin{gather*} L=\mathrm{E}_{q(\mathrm{Z|X, A)}}[\log p(A \mid Z)]- \\ K L(q(Z \mid X, A) \| p(Z)) \end{gather*} $ | (5) |
其中,KL(.)表示两个概率分布之间的Kullback-Leibler散度。最后,对生成的低维表征进行下游聚类,获得细胞亚群聚类标签。聚类标签与金标准进行比较,验证聚类方法的准确性。
1.2 图神经网络本文采用简化图卷积(Simple graph convolution, SGC)嵌入到变分自编码器中,用以计算低维表征。简化图卷积在原有的图卷积神经网络(GCN)[20]上进行修改,以修正模型复杂性和冗余计算。通过减少连续层之间的折叠权重矩阵和非线性来简化计算,提升效率。这种简化的线性模型在理论和实验中被证明具有更好的性能,其中的卷积核被修改为线性模式:
| $ \begin{align*} \hat{Y}_{S G C} & ={soft\max}\left(S \ldots S S X {\bf{\Theta }}^{(1)} {\bf{\Theta }}^{(2)} \ldots {\bf{\Theta }}^{(K)}\right) \\ & ={soft\max}\left(S^{K} X {\bf{\Theta }}\right) \end{align*} $ | (6) |
其中S是归一化邻接矩阵,X是特征矩阵,Θ是权重矩阵,softmax表示归一化指数函数。
1.3 空间转录组验证数据集本文采用最常用的空间转录组学数据集来验证细胞亚群聚类算法的准确性。这个数据集是关于人类背外侧前额叶皮层(Human DLPFC),原始数据可在10x Visium数据存储库中获取,包括基因表达谱、空间位置信息和组织学图像。该数据集相应的细胞亚群注释金标准可以在SpatialLIBD项目[21]中找到。
该数据集包含12个组织切片,每个切片的捕捉位点从3 460到4 789不等,测序的基因数量为33 538个。样本名称标记为151 507到151 676。在人工注释中,每个样本包含五或七个细胞亚群,包含两类细胞,即DLPFC层和白质。每个细胞亚群具有清晰的边界,因此这个数据集非常适合用于聚类准确度评估。将提出的聚类方法与多个基准方法在这个数据集上进行比较,以评估它们的聚类准确性。此外,每个样本包含的细胞亚群均按时间顺序排列的,因此该数据集也适合空间轨迹推断评估。
1.4 评价指标在空间转录组数据集拥有人工注释的情况下,可以通过调整兰德指数(ARI)来评估细胞亚群聚类的准确性。本文使用的人类背外侧前额叶皮层拥有金标准,因此通过融合预测标签和金标准来计算调整兰德指数。设P={P1, P2, …Pc}和G={G1, G2, …Gc}分别为预测标签和人工注释标签,则调整兰德指数可以由下面的公式计算得到:
| $ \begin{array}{l} ARI = \\ \frac{{\sum {_{i, j}\left( {\begin{array}{*{20}{c}} {{n_{ij}}}\\ 2 \end{array}} \right) - \left[ {\sum {_i\left( {\begin{array}{*{20}{c}} {{n_{i.}}}\\ 2 \end{array}} \right)\sum {_j\left( {\begin{array}{*{20}{c}} {{n_{.\mathit{j}}}}\\ 2 \end{array}} \right)} } } \right]/} \left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right)}}{{\frac{1}{2}\left[ {\sum {_i\left( {\begin{array}{*{20}{c}} {{n_{i.}}}\\ 2 \end{array}} \right) + \sum {_j\left( {\begin{array}{*{20}{c}} {{n_{.\mathit{j}}}}\\ 2 \end{array}} \right)} } } \right] - \left[ {\sum {_i\left( {\begin{array}{*{20}{c}} {{n_{i.}}}\\ 2 \end{array}} \right)\sum {_j\left( {\begin{array}{*{20}{c}} {{n_{.\mathit{j}}}}\\ 2 \end{array}} \right)} } } \right]/\left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right)}} \end{array} $ | (7) |
其中,c代表细胞亚群的个数,ni.和n.j表示属于第i类预测标签和第j类人工注释标签的个数,nij则是同时属于第i类预测标签和第j类人工注释标签的细胞个数。调整兰德指数的取值范围是[0, 1],在本文中由scikit-learn工具包中的adjusted_rand_score函数来计算,其值越高,则细胞亚群聚类的精度越高。
1.5 神经网络超参数的选取基于变分自编码器的聚类方法是在Python中利用PyTorch_pyG [22]实现。首先,在Scanpy工具箱[23]中对基因表达谱进行标准化和对数转换,遴选3 000个高度可变基因来得到特征矩阵; 然后,利用scikit-learn工具包[24]中的最近邻搜索技术来计算邻接矩阵,每个细胞的邻居通过K最近邻法来获取,其中K值取6。接着,将特征矩阵和邻接矩阵输入到构建的变分自编码器中生成低维表征。相关的超参数定义如下:输入维度为3 000(高变基因数),隐藏维度为128,输出维度为30。学习率为1×10-6,迭代次数为5 000,权重衰减因子为1×10-4,梯度剪裁为5,随机种子为零。隐藏层的数量为4,每个层外的激活函数为指数线性单元(ELU)函数。本文采用的硬件平台规格为Ubuntu 20.04.5 LTS系统搭配i9-12900F CPU,64G内存和GeForce RTXTM3090Ti GPU。
计算得到低维表征后,采用传统的Kmeans聚类方法来聚类细胞亚群,并在scikit-learn软件包中实现。Kmeans方法中,细胞亚群的个数设置为与金标准的个数相同,得到预测细胞亚群标签。最后,根据预测细胞标签和人工注释标签,计算调整兰德指数,比较调整兰德指数的大小来说明各种方法的准确性。本文用到的基准方法包括Scanpy[23], SpaGCN[25], SEDR[26], STAGATE[27], DeepST[28], BayesSpace[29]等,它们均是先进的基于图神经网络的空间转录组细胞亚群聚类和空间域识别算法。
2 结果与讨论 2.1 聚类准确度比较本文提出的细胞亚群聚类和空间域识别方法命名为VGAE_SGC。将VGAE_SGC与六种空间聚类基准方法(Scanpy, SpaGCN, SEDR, STAGATE, DeepST, BayesSpace)进行比较, 来说明其准确性和有效性。将上述七种方法在人类背外侧前额叶皮层(Human DLPFC)空间转录数据集上进行比较,计算每种方法在12个样本上的调整兰德指数(ARI),生成ARI平均值。
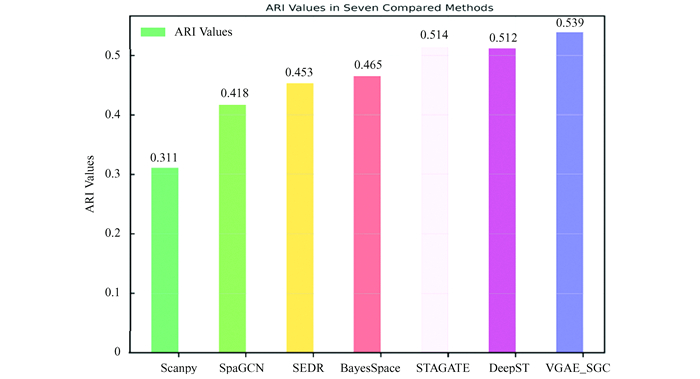
图 2展示了每种方法在Human DLPFC数据上的调整兰德指数平均值,可以看到本文提出的VGAE_SGC方法拥有最大的ARI (0.539)。在七种方法中,有三种方法的ARI平均值超过了0.5,分别是VGAE_SGC,DeepST和STAGATE。同时,Scanpy中采用传统的Leiden算法进行细胞亚群聚类,并没有利用空间转录数据中的空间位置信息,因此它对应的平均ARI值最低,为0.311。SpaGCN, SEDR和BayesSpace的精度处于中间位置,ARI值均在0.45左右。图 2说明本文提出的方法在聚类精度方面能够优于存在的细胞亚群聚类方法。
|
图 2 空间转录组细胞亚群聚类方法平均ARI Figure 2 Average ARI values for cell clustering of spatial transcriptomics |
为了进一步说明VGAE_SGC在空间域识别方面的优势,以Human DLPFC数据集中的单个样本为例,来展示七种方法的空间域识别结果。本文选取样本151 675来展示结果,图 3是每种方法在该样本上的细胞亚群聚类结果。该样本的金标准(Ground truth)中包含7个空间域,每个空间域之间的界限明确,而且空间域之间按一定的时间先后顺序排列。

|
图 3 七种方法的空间转录组数据空间域识别结果比较 Figure 3 Spatial domain identification results of seven compared methods for spatial transcriptomics |
在该样本上,本文提出的VGAE_SGC仍具有最高的ARI值,为0.550。剩余六种基准方法的ARI值均没有超过0.50,以此说明VGAE_SGC在这个样本上的聚类优势。从空间域识别的结果来看,VGAE_SGC和DeepST结果更加接近于金标准,任何两个空间域之间都有明确的分界线。在SpaGCN和Scanpy中,由于两者的ARI较低,对应它们的空间域识别结果也比较差,细胞的分布杂乱无章。图 3说明了本文提出的VGAE_SGC能够更好地利用空间位置信息来定位细胞,从而识别更加准确的空间域。
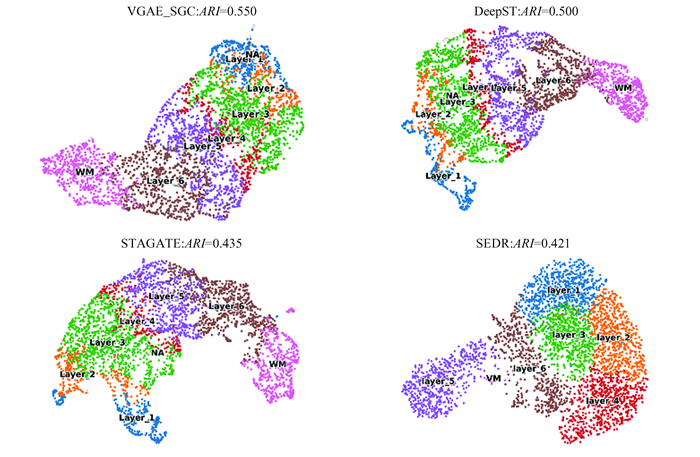
2.3 低维表征质量比较在本文比较的七种方法中,四种方法的低维表征能够获取,从而得到降维聚类图。本节比较四种方法(VGAE_SGC, DeepST, STAGATE和SEDR)的低维表征的质量。具体的降维图展示在图 4中。首先,VGAE_SGC对应的调整兰德指数最大,为0.550。DeepST比较接近VGAE_SGC, ARI值为0.50。它们对应的Umap降维图也比较接近,每个细胞亚群都独立分开,而且按一定先后顺序排列。而在STAGATE和SEDR的降维图中,结果就比较差。比如STAGATE中的Layer_1和Layer_2,SEDR中的细胞亚群错乱的分布,并没有按一定的先后顺序来排列,说明它并没有充分结合基因表达谱和空间位置信息来完成聚类。综上,与已有的空间转录组细胞亚群聚类基准方法相比,上述三部分结果证明了本文提出的VGAE_SGC方法的准确性和有效性。
|
图 4 四种方法中低维表征的Umap降维图 Figure 4 The Umap diagram of latent embedding in four methods |
利用图深度学习来结合空间转录组中基因表达谱和空间位置信息来进行细胞亚群聚类能够有效地提升准确性。本文构建名为VGAE_SGC的空间转录组聚类架构,在变分自编码器中嵌入简化图卷积来处理基因表达谱和空间位置信息。在人类背外侧前额叶皮层(Human DLPFC)空间转录数据集上与多个基准方法进行比较,说明了VGAE_SGC方法在细胞亚群聚类精度、空间域识别的结果和低维表征质量三个方面都有优势,证明了本文提出的基于变分自编码器的空间转录组细胞亚群聚类方法的有效性。本文聚类方法的源代码及其在更多数据集中的聚类结果可见链接https://github.com/narutoten520/Bioinformatics_VGAE_SGC。
| [1] |
NAWY T. Single-cell sequencing[J]. Nature Methods, 2014, 11(1): 18-18. DOI:10.1038/nmeth.2771 (  0) 0) |
| [2] |
卢汀. 生物信息学基因表达差异分析[J]. 生物信息学, 2014, 12(2): 140-144. LU Ting. Bioinformatics analysis for gene differential expression[J]. Chinese Journal of Bioinformatics, 2014, 12(2): 140-144. DOI:10.3969/j.issn.1672-5565.2014-02.20140210 (  0) 0) |
| [3] |
许醒, 蔡林峰, 张倩楠, 等. 单细胞与空间转录组分析研究进展[J]. 分析测试学报, 2022, 41(9): 1322-1334. XU Xing, CAI Linfeng, ZHANG Qiannan, et al. Advances in single-cell and spatial transcriptome analysis[J]. Journal of Analytical Testing, 2022, 41(9): 1322-1334. DOI:10.19969/j.fxcsxb.22052401 (  0) 0) |
| [4] |
WILLIAMS C G, LEE H J, ASATSUMA T, et al. An introduction to spatial transcriptomics for biomedical research[J]. Genome Medicine, 2022, 14(1): 1-18. DOI:10.1186/s13073-022-01075-1 (  0) 0) |
| [5] |
RODRIQUES S G, STICKELS R R, GOEVA A, et al. Slide-seq: A scalable technology for measuring genome-wide expression at high spatial resolution[J]. Science, 2019, 363(6434): 1463-1467. DOI:10.1126/science.aaw1219 (  0) 0) |
| [6] |
NICHTERWITZ S, CHEN G, AGUILA BENITEZ J, et al. Laser capture microscopy coupled with Smart-seq2 for precise spatial transcriptomic profiling[J]. Nature Communications, 2016, 7(1): 12139. DOI:10.1038/ncomms12139 (  0) 0) |
| [7] |
XIA Keke, SUN Haixi, LI Jie, et al. Single-cell Stereo-seq enables cell type-specific spatial transcriptome characterization in Arabidopsis leaves[J]. bioRxiv, 2021, 2021. DOI:10.1101/2021.10.20.465066 (  0) 0) |
| [8] |
RAO N, CLARK S, HABERN O. Bridging genomics and tissue pathology: 10x genomics explores new frontiers with the visium spatial gene expression solution[J]. Genetic Engineering & Biotechnology News, 2020, 40(2): 50-51. DOI:10.1089/gen.40.02.16 (  0) 0) |
| [9] |
王琳, 赵桂华. 用于空间分辨转录组学数据分析的统计方法[J]. Bioprocess, 2023, 13: 57. WANG Lin, ZHAO Guihua. Statistical methods for spatially re-solved transcriptomic data analysis[J]. Bioprocess, 2023, 13: 57. DOI:10.12677/BP.2023.131008 (  0) 0) |
| [10] |
SATIJA R, FARRELL J A, GENNERT D, et al. Spatial reconstruction of single-cell gene expression data[J]. Nature Biotechnology, 2015, 33(5): 495-502. DOI:10.1038/nbt.3192 (  0) 0) |
| [11] |
WOLF F A, ANGERER P, THEIS F J. SCANPY: Large-scale single-cell gene expression data analysis[J]. Genome Biology, 2018, 19: 1-5. DOI:10.1186/s13059-017-1382-0 (  0) 0) |
| [12] |
PALLA G, SPITZER H, KLEIN M, et al. Squidpy: A scalable framework for spatial omics analysis[J]. Nature methods, 2022, 19(2): 171-178. DOI:10.1038/s41592-021-01358-2 (  0) 0) |
| [13] |
宋东奇, 宋余庆, 刘哲, 等. 新型适用于基因表达数据的模型聚类方法[J]. 计算机与应用化学, 2015, 32(1): 71-74. SONG Dongqi, SONG Yuqing, LIU Zhe, et al. Novel model clustering approach for gene expression data[J]. Computer and Applied Chemistry, 2015, 32(1): 71-74. DOI:10.3390/diagnostics10080584 (  0) 0) |
| [14] |
TRAAG V A, WALTMAN L, VAN ECK N J. From louvain to leiden: Guaranteeing well-connected communities[J]. Scientific Reports, 2019, 9(1): 5233. DOI:10.1038/s41598-019-41695-z (  0) 0) |
| [15] |
HAUGHTON D, LEGRAND P, WOOLFORD S. Review of three latent class cluster analysis packages: Latent Gold, poLCA, and MCLUST[J]. The American Statistician, 2009, 63(1): 81-91. DOI:10.1198/tast.2009.0016 (  0) 0) |
| [16] |
CHATZIS S P, TSECHPENAKIS G. The infinite hidden Markov random field model[J]. IEEE Transactions on Neural Networks, 2010, 21(6): 1004-1014. DOI:10.1109/TNN.2010.2046910 (  0) 0) |
| [17] |
MO Qianxing, SHEN Ronglai, GUO Cui, et al. A fully Bayesian latent variable model for integrative clustering analysis of multi-type omics data[J]. Biostatistics, 2018, 19(1): 71-86. DOI:10.1093/biostatistics/kxx017 (  0) 0) |
| [18] |
王国力, 孙宇, 魏本征. 医学图像图深度学习分割算法综述[J]. 计算机工程与应用, 2022, 58(12): 37-50. WANG Guoli, SUN Yu, WEI Benzheng. Systematic review on graph deep learning in medical image segmentation[J]. Computer Engineering and Applications, 2022, 58(12): 37-50. DOI:10.3778/j.issn.1002-8331.2112-0225 (  0) 0) |
| [19] |
KIPF T N, WELLING M. Variational graph auto-encoders[J]. arXiv preprint arXiv: 1611.07308, 2016. DOI: 10.48550/arXiv.1611.07308.
(  0) 0) |
| [20] |
ZHANG Si, TONG Hanghang, XU Jiejun, et al. Graph convolutional networks: A comprehensive review[J]. Computational Social Networks, 2019, 6(1): 1-23. DOI:10.1186/s40649-019-0069-y (  0) 0) |
| [21] |
PARDO B, SPANGLER A, WEBER L M, et al. SpatialLIBD: An R/Bioconductor package to visualize spatially-resolved transcriptomics data[J]. BMC Genomics, 2022, 23(1): 1-5. DOI:10.1186/s12864-022-08601-w (  0) 0) |
| [22] |
FEY M, LENSSEN, J E. Fast graph representation learning with PyTorch Geometric[J]. arXiv preprint: 1903.02428, 2019. DOI: 10.48550/arXiv.1903.02428.
(  0) 0) |
| [23] |
WOLF F A, ANGERER P, THEIS F J. SCANPY: Large-scale single-cell gene expression data analysis[J]. Genome Biology, 2018, 19(1): 1-5. DOI:10.1186/s13059-017-1382-0 (  0) 0) |
| [24] |
PEDREGOSA F, VAROQUAUX G, GRAMFORT A, et al. Scikit-learn: Machine learning in Python[J]. The Journal of Machine Learning Research, 2011, 12: 2825-2830. DOI:10.48550/arXiv.1201.0490 (  0) 0) |
| [25] |
HU Jian, LI Xiangjie, COLEMAN K, et al. SpaGCN: Integrating gene expression, spatial location and histology to identify spatial domains and spatially variable genes by graph convolutional network[J]. Nature Methods, 2021, 18(11): 1342-1351. DOI:10.1038/s41592-021-01255-8 (  0) 0) |
| [26] |
FU Huazhu, XU Hang, CHONG K, et al. Unsupervised spatially embedded deep representation of spatial transcriptomics[J]. Biorxiv, 2021, 2021. DOI:10.1101/2021.06.15.448542 (  0) 0) |
| [27] |
DONG Kangning, ZHANG Shihua. Deciphering spatial domains from spatially resolved transcriptomics with an adaptive graph attention auto-encoder[J]. Nature Communications, 2022, 13(1): 1739. DOI:10.1038/s41467-022-29439-6 (  0) 0) |
| [28] |
XU Chang, JIN Xiyun, WEI Songren, et al. DeepST: Identifying spatial domains in spatial transcriptomics by deep learning[J]. Nucleic Acids Research, 2022, 50(22): e131-e131. DOI:10.1093/nar/gkac901 (  0) 0) |
| [29] |
ZHAO E, STONE M R, REN Xing, et al. Spatial transcriptomics at subspot resolution with BayesSpace[J]. Nature Biotechnology, 2021, 39(11): 1375-1384. DOI:10.1038/s41587-021-00935-2 (  0) 0) |
 2024, Vol. 22
2024, Vol. 22


