2. 中国农业大学 生物学院, 北京 100193
2. College of Biological Sciences, China Agricultural University, Beijing 100193, China
群体之间发生单倍体混合是一种常见的现象,为研究物种的表型变异和与环境适应性相关提供了视角。局部祖先推断(Local ancestry inference, LAI),也称作局部祖先反褶积,是全基因组遗传分析的重要内容[1-2]。LAI用于对混合单倍体的评估,并且在特定的片段上计算来自不同祖源群体的拷贝数量。分析杂交后代每条单倍体片段上的祖先来源,为研究基因混合的群体历史和推断基因流的动态过程提供了基础[3-4]。将一些有利或不利的等位基因通过相应的祖先来源进行定位,有助于在野生种群中发现宝贵的遗传资源,同时有助于研究驯化种群的适应性,并根据人类需求进行品种改良[5-6]。
计算技术、基因测序和单核苷酸多态性(Single nucleotide polymorphism, SNP) 基因分型方法的快速发展使得利用全基因组信息推断杂交后代局部祖源成为可能[7]。在LAI模型中,每条染色体被认为是起源于多个祖先群体的马赛克片段嵌合体[3, 8]。在已经发表的模型中均以染色体为单位来推断局部祖源,其中大多数模型采用HMMs, HMMs家族或动态规划(Dynamic planning, DP)算法。这些算法提供一个简洁高效的计算框架,将混合祖源个体的染色体可划分为若干个连续的单倍型片段,每个片段来自一个特定的祖先群体[9]。在窗口的选择上,一些模型采用连锁不平衡(Linkage disequilibrium, LD) 模型划分单倍型[4],例如:STRUCTURE[10],Saber[11], Hapmix和LAMP-LD等,另外一些模型则采用滑窗的策略,例如:RFMix, PCAdmix[12]和LAMP[13]等。
每种模型对于混合个体的祖源推断都有各自的优缺点[14]。尽管研究者已经做出了很多努力,然而此研究仍面临着诸多挑战。通常这些模型均需要使用者提供多个参数,在实际应用中会对使用者,尤其对于非模式物种的研究人员,造成很大的不便。例如HAPMIX需要使用者提供遗传图谱、重组率和突变率、平均祖先系数以及混合后的平均世代数等一些难以获得的参数;LAMP-LD需要遗传图谱,HMMs中隐藏状态的数量和片段大小等;RFMIX则需要包括遗传图谱,片段大小和混合后的平均代数等。混合单倍型是可变长度的片段,但现有模型通常在群体中将所有单倍体使用一个固定大小的片段进行简化。由于混合世代数与祖源单倍型的片段长度成反比,且世代数很难进行有效评估,所以对于判断祖源单倍型的片段长度或重组断点位置造成一定的困难。错误的判断会降低模型的精度,从而降低LAI的准确性。
基于上述的挑战,本研究提出了一种改进的LAI模型WAdmix,方法致力于对来自不同祖源的不等长片段进行划分。模型对杂交后代的单倍型片段划分采用k-mer评分来确定,而后采用隐马尔科夫模型(Hidden Markov models, HMMs) 在混合单倍体片段中平滑祖源分配,此方法接近于无参数。采用人类2祖源群体和3祖源群体进行杂交后代的模拟评估,以及采用家鸡的2祖源群体进行杂交后代的模拟评估,提示本模型在生物意义上优于那些基于背景LD的方法。
1 模型设计 1.1 片段长度估计本研究需要将祖源群体和目标混合群体的基因型进行基因分相,用来提升计算精度。加权k-mer打分方法的灵感来自于测序覆盖深度的计算,即为计算映射到特定基因组位置单一reads的总数[15]。本研究方法可描述为:首先,基于祖源群体中所有单倍体的k-mer序列从头至尾生成一个k-mer计数列表,也称为k-mer频数;然后,同样从头至尾计算每个待测混合个体的单倍体上每个碱基位置的加权k-mer得分得到k-mer覆盖度,其方法是以k为单元滑动将所有k-mer计数相加。该方法在一定程度上考虑到了邻近的碱基单倍型信息。给定一个长度为l的混合单倍体,序列中任意位置i的重复得分如公式(1)所示:
| $ {rscore}_i=\sum\limits_{j=0}^n {count}_{m_{i j}}(0<i<l, n \leqslant k) $ | (1) |
其中mij为包含混合单倍体位置i的k-mer, n为mij的个数,countmij为混合单倍体对应的全部祖源群体位置i的mij数量。下图显示了k-mer覆盖度和加权k-mer覆盖度的计算过程(图 1)。在一个长度为19个SNPs的序列中,包含11个多次出现的4-mer,在7~10和12~15的位置上因为没有4-mer映射在此位置上,k-mer的覆盖度为0。4个SNPs的累积得分构成加权k-mer覆盖度。研究设置了一个特定的阈值,低于阈值的特定碱基位置被认为是单倍体的重组断点。通过改变阈值,可以得到不同长度的单倍型片段。
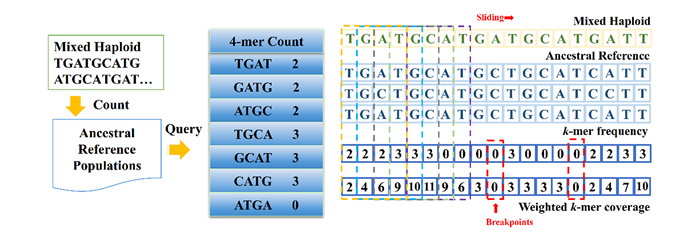
|
图 1 k-mer的计算方法 注: 加权k-mer统计步骤由两部分组成。首先,计算混合单倍体与祖源群体中位置i上所有k-mer的频数。其次,计算在整条单倍体中,特定的位置在k范围内所累积的k-mer频数。重组断点可以通过k-mer频数和加权k-mer覆盖度检测,如0值表示一个特定的阈值,即为重组断点值. |
研究使用HMMs算法来为每个待测个体的每个单倍体片段分派一个祖源。HMMs由两个序列组成:一个观察状态过程为O1, O2, ..., On和一个隐藏状态的过程为A1, A2, ..., An (图 2(a))[16]。在本研究中,祖源状态过程被认为是“隐藏”的变量。Baum-Welch算法对HMMs中的发射和转移概率的参数进行估计,Viterbi算法对HMMs中的局部祖先进行重构和平滑。根据上述k-mer计算,可得到每个单倍体特异的重组断点划分。在获得重组断点后,祖先参考群体之间的重组过程如图所示(图 2(b)),即“亲本”单倍体来自特定的祖源群体,杂交后代的单倍体是亲本单倍体的“马赛克”组合(图 2(c))[17]。
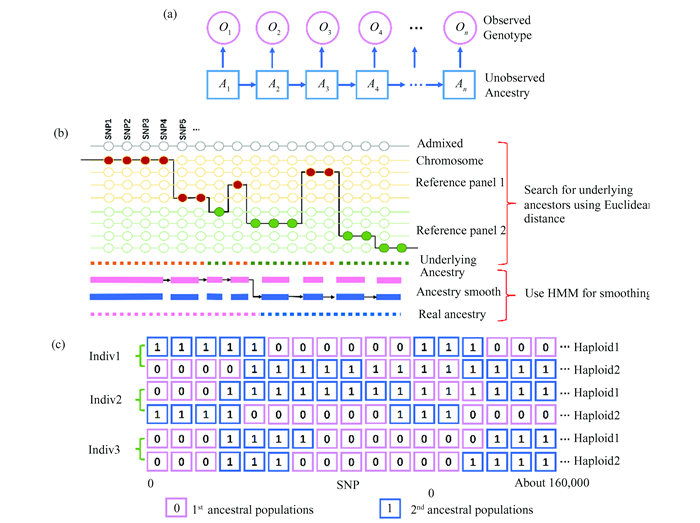
|
图 2 HMMs的计算方法 Figure 2 Calculation method of HMMs 注:(a) 应用于LAI的HMMs示意图; (b) 上方的灰色线表示一个混合单倍体序列,并带有SNPs位点(空圆圈);重组的祖源状态显示在其下方的颜色条中,以及从第一个群体(橙色) 到第二个群体(绿色) 的祖源变化。混合单倍体来自两组不同的祖源,由橙色和绿色水平虚线的片段拼接而成,即祖源群体的混合事件,黑线显示了混合单倍体是如何重新构建的。下方虚线显示了沿着祖源群体进行拷贝,由粉色和蓝色水平虚线的片段拼接而成,在大多数位置上,这与潜在祖先是相同的,但偶尔也会出现“拷贝错误”,即绿色虚线段出现在橙色祖源片段内; (c) 粉色和蓝色为祖源群体的亲本片段集合,将杂交后代的片段模拟为现有亲本片段的拼接,每个单倍体在同一个体中有不同的重组断点.(扫本文首页二维码见彩图). |
对于特定的单倍体划分片段w,qiw, jw表示杂交后代iw的单倍体片段与祖源池中其它对应单倍体片段在序列水平的欧氏距离(Euclidean distance, ED) 的比例(图 3)。qiw, jw的估计值如公式(2) 所示:
| $ q_{i_w, j_w}=D_{i_w, j_w} / \sum\limits_{k_w} D_{i_w, k_w} j_w \in k_w $ | (2) |

|
图 3 观测状态的计算方法 Figure 3 Calculation method of observe state 注: 如3祖源群体的观测状态估计,基于每个独立片段的祖源单倍体拷贝,即混合单倍体,利用欧式距离对其单个片段进行祖源分配. |
其中,Diw, jw为杂交后代特定片段iw到祖源群体jw序列水平的欧氏距离,m为祖源数目,对于每个来自祖源群体kw (2或3祖源) 的混合单倍体片段,与祖源池中的最小距离可获得最大概率的祖源分派,则观察状态如公式(3)所示:
| $ {q^{\prime}}_{i_w, j_w}=\left(1-\left(q_{i_w, j_w} / \sum\limits_{k_w} q_{i_w, k_w}\right)\right) /(m-1) j_w \in k_w $ | (3) |
对于特定的混合单倍体i, qin, jn表示杂交后代in分配到祖先jn的基因组所有片段累计的欧式距离的比例(图 4),qin, jn的估计值如公式(4)所示:
| $ q_{i_n, j_n}=\sum\limits_n D_{i_n, j_n} / \sum\limits_{k_n} \sum\limits_n D_{i_n, k_n} j_n \in k_n $ | (4) |
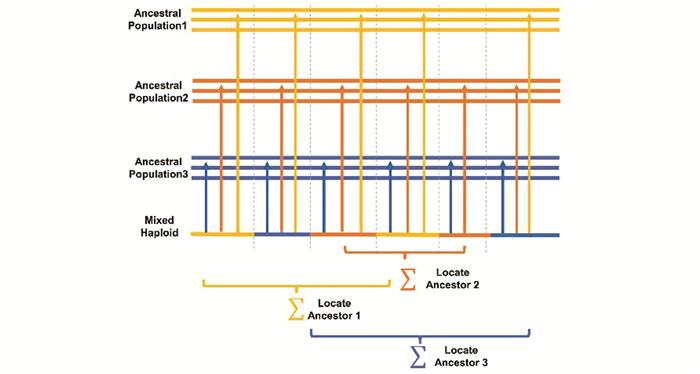
|
图 4 发射概率的计算方法 Figure 4 The calculation method of emission probability 注: 如3祖源混合初始发射概率估计,计算混合单倍体与特定祖源的欧氏距离累积值. |
其中,$\sum\limits_n$Din, jn表示混合单倍体in所有分配到祖源jn片段到相应祖源jn片段累计的欧式距离,n表示片段的数目,m为祖源数目,对于每个来自祖源群体kn (2或3祖源) 的混合单倍体累计片段,与祖源池中的最小距离可获得最大发射概率,q′in, jn表示混合单倍体in的累积片段在混合祖源池中出现的概率,发射概率如公式5所示:
| $ {q^{\prime}}_{i_n, j_n}=\left(1-\left(q_{i_n, j_n} / \sum\limits_{k_n} q_{i_n, k_n}\right)\right) /(m-1) j_n \in k_n $ | (5) |
在HMMs中,转移概率基于单倍体的重组,重组事件的发生可模拟为泊松分布。对于两个祖先群体,祖先状态的转移pw, w+1为(Aw1, Aw2)…其中Aw1代表片段w属于第一个祖源群体,而Aw2属于另一个祖源群体。rw,w+ 1为片段w和片段w + 1每一代的重组率,T为自混合以来的世代数。πA1和πA2分别对应群体1和群体2的初始概率,初始化的转移概率矩阵如公式(6)所示:
| $ P_{w, w+1}=\left[\begin{array}{ll} p_{w, w+1}^{A_1, A_1} & p_{w, w+1}^{A_1, A_2} \\ p_{w, w+1}^{A_2, A_1} & p_{w, w+1}^{A_2, A_2} \end{array}\right]=\left[\begin{array}{cc} 1-\left(1-e^{-r_{w, w+1} T}\right) \pi_{A_1} & \left(1-e^{-r_{w, w+1} T}\right) \pi_{A_1} \\ \left(1-e^{-r_{w, w+1} T}\right) \pi_{A_2} & 1-\left(1-e^{-r_{w, w+1} T}\right) \pi_{A_2} \end{array}\right] $ | (6) |
对于三个祖源群体,祖先状态的转移pw, w+1为(Aw1, Aw2), (Aw2, Aw3) 和(Aw3, Aw1)…其中,Aw1代表片段w属于第一个祖源群体,Aw2和Aw3属于另外两个祖源群体。πA1, πA2和πA3分别对应群体1~3的初始概率,初始化转移概率矩阵如公式(7)所示:
| $ \begin{array}{*{20}{c}} & P_{w, w+1}=\left[\begin{array}{lll} P_{w, w+1}^{A_1, A_1} & P_{w, w+1}^{A_1, A_2} & P_{w, w+1}^{A_1, A_3} \\ P_{w, w+1}^{A_2, A_1} & P_{w, w+1}^{A_2, A_2} & P_{w, w+1}^{A_2, A_3} \\ P_{w, w+1}^{A_3, A_1} & P_{w, w+1}^{A_3, A_2} & P_{w, w+1}^{A_3, A_3} \end{array}\right]= \\ & {\left[\begin{array}{ccc} 1-2\left(1-e^{-r_{u, w+1} T}\right) \pi_{A_1} & \left(1-e^{-r_{w, w+1} T}\right) \pi_{A_1} & \left(1-e^{-r_{w, w+1} T}\right) \pi_{A_1} \\ \left(1-e^{-r_{w, w+1} T}\right) \pi_{A_2} & 1-2\left(1-e^{-r_{w, w+1} T}\right) \pi_{A_2} & \left(1-e^{-r_{w, w+1} T}\right) \pi_{A_2} \\ \left(1-e^{-r_{w, w+1} T}\right) \pi_{A_3} & \left(1-e^{-r_{w, w+1} T}\right) \pi_{A_3} & 1-2\left(1-e^{-r_{w, w+1} T}\right) \pi_{A_3} \end{array}\right]} \end{array} $ | (7) |
为了评估特定数据背景下LAI模型的推断性能,研究采用16只惠阳胡须鸡和14只A系商品鸡,提取高密度基因分型(Genotyping by sequencing, GBS) 的1号染色体 [18-19]。使用Wright-Fisher模型生成混合二倍体个体[20],对于祖源群体和混合群体中的个体,使用Beagle工具进行基因型分相[21]。
2.2 人类群体之间的混合为了评估本研究模型的性能,参考其它LAI模型的模拟方式,模拟的混合单倍体分别采用2祖源和3祖源群体来进行。首先,采用人类单倍型图谱Ⅲ (Haplotype map Ⅲ, HapMap3) [22]已分相样本中的10个祖源群体,每个祖源群体30个个体,分成5组进行模拟。其中包括芬兰群体(Finnish from finland, FIN)和卢希亚群体(Luhya in webuye, kenya,LWK);中国南方汉人群体(Han chinese south, CHS)和LWK群体;托斯卡尼群体(Toscani in Italy, TSI)和墨西哥群体(Mexican ancestry in Los Angeles, California, MSL);中国西双版纳傣族(Chinese dai in xishuangbanna, China, CDX) 和MSL群体;中国南方汉族(Han chinese south, CHS)和FIN群体;CDX群体和TSI群体,这5组为祖先群体。另外,研究采用中国汉族群体(Han chinese in Beijing, China, CHB),欧洲群体(Utah residents with northern and western european ancestry from the CEPH collection, CEU)和非洲群体(Yoruba in ibadan, Nigeria, YRI)各30个个体,进行3祖源群体的混合模拟。同样使用Wright-Fisher模型产生二倍体杂交后代,并对1号染色体进行祖源推断分析。
3 实验设计 3.1 家鸡群体2祖源混合模拟采用50% 惠阳胡须鸡和50% A系商品鸡杂交模式进行祖源混合模拟,共产生30个杂交后代,并运行7个LAI模型进行祖源推断。当设定最小等位基因频率(Minor allele frequency, MAF) < 0.05时,1号染色体上共保留了32 411个SNPs。在祖源推断分析过程中,研究考虑了5种情况的世代数g∈(10, 50, 100, 300, 500),并与Loter[23], RFMix, LAMP-LD, Seqmix[24], Chromopainter[25]和GEDI-ADMX现有模型进行比较,使用二倍体均方误差(Mean squared error, MSE) 的95%的置信区间作为推断性能的比较标准。对于常用的工具RFMix,二倍体MSE随着混合代数的增加也随之增加,混合代数为10时,MSE平均值为1.3%,500代时误差为25.1%;相比较下,Loter和LAMP-LD的精度较高,其二倍体MSE平均值在0.6%~7.4%和4.7%~6.5%;Seqmix,Chromopainter和GEDI-ADMX在模拟家鸡群体的数据上表现不佳。相对于其它模型,本研究模型(WAdmix) 表现出中等的MSE平均值评估,混合代数为10时,二倍体MSE平均值估计为7.1%,混合代数为500时,二倍体MSE平均值为18.5%。箱线图展示了30个个体值的二倍体MSE估计值分布(图 5)。
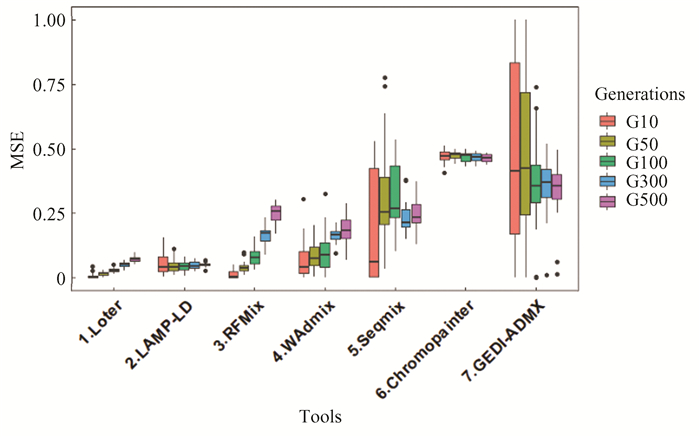
|
图 5 利用惠阳胡须鸡和A系商品鸡对LAI模型进行比较评估 Figure 5 LAI models were evaluated using Huiyang Bearded and high-quality chicken Line A |
研究采用与上述相似的方法构建FIN/LWK,CHS/LWK,TSI/MSL,CDX/MSL, CHS/FIN和CDX/TSI独立的6组模拟杂交后代,其中g∈(10, 50, 100, 150, 200) 代,杂交模式均为50%/50%。群体数据集来自HapMap3项目的已分相数据作为祖源参考群体,并采用两个祖源群体作为参考群体,结合wright-fisher模型构建杂交后代的基因型信息,分别对每个杂交后代的1号染色体进行LAI分析。SNPs过滤标准设定为MAF ≤0.25,其中6组模拟混合群体过滤后保留的SNPs数目为212 322~230 438。
对于6组模拟分析,二倍体MSE的置信区间值仍设置为95%。以FIN/LWK为例,RFMix对二倍体MSE的估计值随着世代数的增加而增加,从10代MSE平均值为0.4% 增加到200代时平均值为18.7%。Loter再次显示了最佳的性能,相应的MSE平均值估计在0.6%~5.2%。本研究模型(WAdmix) 在世代数为10时,二倍体的MSE平均值为17.1%,世代数200代时二倍体的MSE平均值为14.5%。箱线图显示了30个个体的二倍体MSE估计值分布(图 6)。
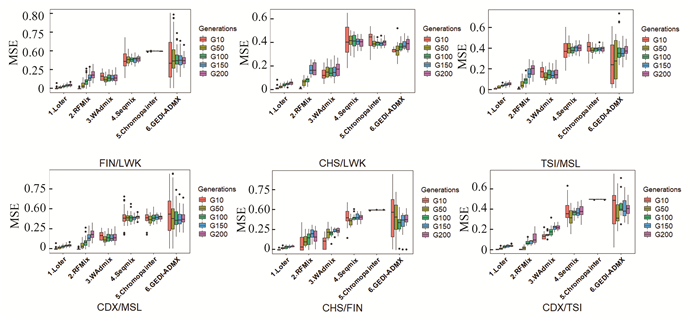
|
图 6 采用6组人类两祖源群体对LAI模型进行比较评估 Figure 6 LAI model was evaluated by using six groups of human two-ancestral populations |
在3祖源混合人类群体中,通过Loter,RFMix,Chromopainter和GEDI-ADMX获得模拟混合个体的二倍体MSE估计,置信区间为95%。杂交后代是通过YRI, CEU和CHS祖源群体模拟出来的,在g∈(10, 50, 100, 150, 200) 代时,分别产生30个混合模拟个体,杂交模式均为33%/33%/34%。研究发现,当世代数从10代增加到200代时,Loter的二倍体MSE估计略有变化,平均值从0.7%~4.0% 不等。对于RFMix,平均值从5.0%~12.7% 不等。同样与其它模型比较,本研究的模型(WAdmix) 表现出中等精度,在10代前的二倍体MSE平均值估计为15.5%,在200代时的二倍体MSE平均值估计为28.0%。如箱线图显示了30个二倍体杂交后代的MSE估计值分布(图 7)。
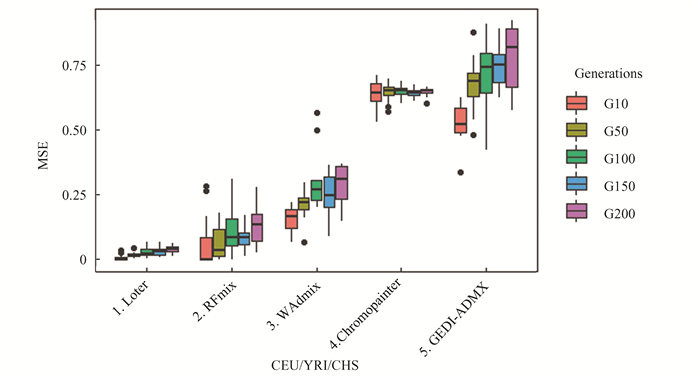
|
图 7 采用一组人类3祖源群体对LAI模型进行比较评估 Figure 7 LAI model was evaluated by using one group of human three-ancestral populations |
大多数主流模型均以个体为单位进行祖源定长片段划分,本文提出了一种改进的LAI模型,用于推断杂交后代的祖先起源。研究致力于在任一单倍体中采用不定长的祖源片段划分,每个单倍体片段都具有不同的祖先来源。本模型主要基于k-mer和HMMs目标函数优化策略,并需要提供世代数和重组率作为参数,以及用于控制混合单倍体片长度的参数k。这些参数基于群体遗传的实际意义,在使用HMMs来对混合单倍体中祖先群体之间的重组进行建模时,这两个参数不可避免。但当参数难以获得时,研究模型采用了一个平均的参数值来简化选择。另一方面,由于混合的世代数与祖源片段的长度成反比,可采用不同的调控参数k-mer值进行局部祖源片段划分,以此来控制窗口的大小,动态的k-mer值可以有效的改进推断精度。正如预期,不同的k-mer值适用于不同的历史混合事件,对于300 ~ 500代,k-mer设置为8较优,对于较短世代数,k-mer设置为16较优。虽然本研究模型的调控参数依赖于世代数和重组率的经验知识,但大量结果表明,此模型在面对参数不确定时具有稳定性,当参数不能准确获得时,建议采用平均的调控参数。后续研究中,希望能更进一步提高模型的精度与性能;模型将会考虑更多生物现象,获得更多具有生物意义的统计结果;也将展开对特定物种的研究,更细致地分析其基因流的动态过程。
| [1] |
WU Jie, LIU Yangxiu, ZHAO Yiqiang. Systematic review on local ancestor inference from a mathematical and algorithmic perspective[J]. Frontiers in Genetics, 2021, 12: 639877. DOI:10.3389/fgene.2021.639877 (  0) 0) |
| [2] |
GEZA E, MUGO J, MULDER N J, et al. A comprehensive survey of models for dissecting local ancestry deconvolution in human genome[J]. Briefings in Bioinformatics, 2019, 20(5): 1709-1724. DOI:10.1093/bib/bby044 (  0) 0) |
| [3] |
SCHUMER M, POWELL D L, CORBETT-DETIG R. Versatile simulations of admixture and accurate local ancestry inference with mixnmatch and ancestryinfer[J]. Molecular Ecology Resources, 2020, 20(4): 1141-1151. DOI:10.1111/1755-0998.13175 (  0) 0) |
| [4] |
CHAPMAN N H, THOMPSON E A. Linkage disequilibrium mapping: the role of population history, size, and structure[J]. Advances in Genetics, 2001, 42: 413-37. DOI:10.1016/s0065-2660(01)42034-7 (  0) 0) |
| [5] |
WANG D R, HAN Rongkui, WOLFRUM E J, et al. The buffering capacity of stems: Genetic architecture of nonstructural carbohydrates in cultivated Asian rice, Oryza sativa[J]. New Phytologist, 2017, 215(2): 658-671. DOI:10.1111/nph.14614 (  0) 0) |
| [6] |
FITAK R R, RINKEVICH S E, CULVER M. Genome-wide analysis of SNPs is consistent with no domestic dog ancestry in the endangered mexican wolf (Canis lupus baileyi)[J]. Journal of Heredity, 2018, 109(4): 372-383. DOI:10.1093/jhered/esy009 (  0) 0) |
| [7] |
KIDD J M, GRAVEL S, BYRNES J, et al. Population genetic inference from personal genome data: impact of ancestry and admixture on human genomic variation[J]. American Journal of Human Genetics, 2012, 91(4): 660-671. DOI:10.1016/j.ajhg.2012.08.025 (  0) 0) |
| [8] |
PERIS D, LANGDON Q K, MORIARTY R V, et al. Complex ancestries of lager-brewing hybrids were shaped by standing variation in the wild yeast saccharomyces eubayanus[J]. PLoS Genetics, 2016, 12(7): e1006155. DOI:10.1371/journal.pgen.1006155 (  0) 0) |
| [9] |
BARAN Y, PASANIUC B, SANKARARAMAN S, et al. Fast and accurate inference of local ancestry in Latino populations[J]. Bioinformatics, 2012, 28(10): 1359-1367. DOI:10.1093/bioinformatics/bts144 (  0) 0) |
| [10] |
PRITCHARD J K, STEPHENS M, DONNELLY P. Inference of population structure using multilocus genotype data[J]. Genetics, 2000, 155(2): 945-959. DOI:10.1093/genetics/155.2.945 (  0) 0) |
| [11] |
TANG Hua, CORAM Mei, WANG Pei, et al. Reconstructing genetic ancestry blocks in admixed individuals[J]. American Journal of Human Genetics, 2006, 79(1): 1-12. DOI:10.1086/504302 (  0) 0) |
| [12] |
BRISBIN A, BRYC K, BYRNES J, et al. PCAdmix: Principal components-based assignment of ancestry along each chromosome in individuals with admixed ancestry from two or more populations[J]. Human Biology, 2012, 84(4): 343-364. DOI:10.3378/027.084.0401 (  0) 0) |
| [13] |
SANKARARAMAN S, SRIDHAR S, KIMMEL G, et al. Estimating local ancestry in admixed populations[J]. American Journal of Human Genetics, 2008, 82(2): 290-303. DOI:10.1016/j.ajhg.2007.09.022 (  0) 0) |
| [14] |
PASANIUC B, SANKARARAMAN S, KIMMEL G, et al. Inference of locus-specific ancestry in closely related populations[J]. Bioinformatics, 2009, 25(12): i213-i221. DOI:10.1093/bioinformatics/btp197 (  0) 0) |
| [15] |
FENG Cong, DAI Min, LIU Yongjing, et al. Sequence repetitiveness quantification and de novo repeat detection by weighted k-mer coverage[J]. Briefings in Bioinformatics, 2021, 22(3): bbaa086. DOI:10.1093/bib/bbaa086 (  0) 0) |
| [16] |
WU Jie, ZHAO Yiqiang. Machine learning technology in the application of genome analysis: A systematic review[J]. Gene, 2019, 705: 149-156. DOI:10.1016/j.gene.2019.04.062 (  0) 0) |
| [17] |
DOUGHERTY M L, NUTTLE X, PENN O, et al. The birth of a human-specific neural gene by incomplete duplication and gene fusion[J]. Genome Biology, 2017, 18(1): 49. DOI:10.1186/s13059-017-1163-9 (  0) 0) |
| [18] |
ZHANG Chunyuan, LIN Deng, WANG Yuzhe, et al. Widespread introgression in Chinese indigenous chicken breeds from commercial broiler[J]. Evolutionary Applications, 2019, 12(3): 610-621. DOI:10.1111/eva.12742 (  0) 0) |
| [19] |
BU Lina, WANG Qi, GU Wenjie, et al. Improving read alignment through the generation of alternative reference via iterative strategy[J]. Scientific Reports, 2020, 10(1): 18712. DOI:10.1038/s41598-020-74526-7 (  0) 0) |
| [20] |
ZHANG Rui, LIU Chang, YUAN Kai, et al. AdmixSim 2: a forward-time simulator for modeling complex population admixture[J]. BMC Bioinformatics, 2021, 22(1): 506. DOI:10.1186/s12859-021-04415-x (  0) 0) |
| [21] |
BROWNING B L, TIAN Xiaowen, ZHOU Ying, et al. Fast two-stage phasing of large-scale sequence data[J]. American Journal of Human Genetics, 2021, 108(10): 1880-1890. DOI:10.1016/j.ajhg.2021.08.005 (  0) 0) |
| [22] |
The International HapMap Consortium. The International HapMap Project[J]. Nature, 2003, 426(6968): 789-796. DOI:10.1038/nature02168 (  0) 0) |
| [23] |
DIAS-ALVES T, MAIRAL J, BLUM M G B. Loter: A software package to infer local ancestry for a wide range of species[J]. Molecular Biology and Evolution, 2018, 35(9): 2318-2326. DOI:10.1186/s13059-017-1163-9 (  0) 0) |
| [24] |
HU Youna, WILLER C, ZHAN Xiaowei, et al. Accurate local-ancestry inference in exome-sequenced admixed individuals via off-target sequence reads[J]. American Journal of Human Genetics, 2013, 93(5): 891-899. DOI:10.1016/j.ajhg.2013.10.008 (  0) 0) |
| [25] |
LAWSON D J, HELLENTHAL G, MYERS S, et al. Inference of population structure using dense haplotype data[J]. PLoS Genetics, 2012, 8(1): e1002453. DOI:10.1371/journal.pgen.1002453 (  0) 0) |
 2024, Vol. 22
2024, Vol. 22


