人体内定殖着数万亿有益于身心健康的微生物,通常不同的微生物群落定殖在不同的人体部位。研究表明不同人同一部位的微生物群落组成差异很大,同一个人的不同部位的微生物群落组成也显著不同。近年来,越来越多的研究表明人类的疾病与微生物的分布有关。例如,Hill-Burns等[1]的研究成果中就找到了将帕金森氏症与肠道微生物群联系起来的证据,Oren等[2]计算了JS、BC、加权和非加权UniFrac距离的根平方和无平方,并选择了具有PAM算法中使用的预测强度和轮廓指数的集群数量。与Koren的方法不同,Hong等[3]应用了具有欧几里得距离的K均值来识别两个集群,他们认为集群的数量在他们的研究中具有生物学意义。Holmes等[4]Dirichlet多项式混合物(DMM),用于微生物元基因组学数据的概率建模,混合成分将群落聚集到不同的“元社区”,从而确定环境型或肠型,即组成相似的社区群落。Dong M等[5]用Dirichlet多项式模型生成的三个模拟数据集和与帕金森病相关的真实肠道微生物群数据进行了实证研究,以调查三种预测分析策略的性能。Chen J等[6]提出稀疏的Dirichlet回归可以更好地识别微生物组相关的协变量。Yang Y等[7]提出了一种计算模型,即k-Lognormal-Dirichlet-Multinomial模型(kLDM)。Shi Y等[8]通过采用贝叶斯建模方法,能够从数据中了解集群的数量。A Monleon-Getino使用基于马尔可夫链蒙特卡罗模拟(MCMC)的贝叶斯方法来计算稀疏曲线期间OTU的最大预期数量。Irannia ZB等[9]开发了一个马尔科夫随机场模型来预测未知微生物的分类群。Mao J等[10]引入Dirichlet树多项式混合物(DTMM)作为微生物组研究中扩增子序列数据的生成模型。Niccolai E等[11]找到了肠道微生物群的不健康状态通常是短链脂肪酸(SCFA)浓度的降低的原因。Harris K等[12]使用分层的Dirichlet过程,为多站点UNTB开发了一种高效的贝叶斯拟合策略,Yu P等[13]开发了一种计算对数可能性的新方法,以解决不产生长期运行时间的不稳定问题。
针对上述问题,本文提出了一种狄利克雷过程混合模型(DPMM)与K-means聚类相结合的方法,实验结果表明,改进后的算法选取的初始聚类中心点唯一,并且保证了聚类结果的稳定性,与传统K-means等聚类算法相比,聚类准确性和聚类质量都得到了提高。
1 K-means算法K-means算法是有MacQueen于1967年总结多个领域学术成果后提出的,并提一次给出K均值的算法步骤,并用数学方法进行了证明。K均值是机器学习中一种无监督的学习算法。K均值的核心思想是给定一个数据集,它有n条数据记录,要把它分成K类。那么,最后所分的类,类间相似度最小,类内相似度最大。
从算法的核心思想可以看出,K均值在迭代过程中,类内的惩罚函数不断变小,最终保证惩罚函数收敛。K均值最大的缺点在于初始化过程中K的选择。鉴于K的值相较于数据集不会太大。往往采用枚举的方式进行测算。K均值的惩罚函数往往选用欧式距离。具体步骤如下:
假设将n个m维数据X分成K类。
1) 选择K个样本作为初始的聚类中心O;
| $ O=\left\{X_i, X_j, \cdots, X_k\right\}, i \neq j \neq k<K $ | (1) |
2) 针对每个样本计算其距离聚类中心距离D,并计算代价函数L(Xn, O),并将距离最小的样本与聚类中心归为一类Cm;
| $ \quad D=\left\{\left\|X_n-O_m\right\|\right\}, i \neq j \neq k \neq n<K \cap m=1 \text {, }\\ \cdots, K $ | (2) |
| $ C_m=\left\{\left\{X_n \mid L\left(X_n, O\right)=min \left(L\left(X_n, O\right)\right)\right\}, O_m\right\} $ | (3) |
其中,min(*)为最小值。
3) 对每类求算数平均作为新的聚类中心;
| $ O_m=\frac{\sum C_m}{{len}\left(C_m\right)} $ | (4) |
其中,len(*)为集合长度。
4) 重复2、3步操作,知道代价函数达L到终止条件L0,并生成最终结果Y。
对于n个m维数据分成K类的时间复杂度为O(tKnm),空间复杂度O(m(n+K)),其中t为迭代次数。
构建拓扑见图 1。

|
图 1 K均值数学拓扑图 Figure 1 K-means mathematical topology |
从K-means算法可以看出,K值一旦给定将无法更改,算法会根据K值的不同,产生不同的惩罚函数L,L对K值敏感。而其迭代过程的次数是由终止条件决定。整套算法解释性良好,算法灵活度高。
鉴于K均值原理简单,实现容易,收敛速度快,聚类效果好,算法解释性强,需要主动调参参数少,不需要历史样本。
2 狄利克雷混合过程(DPMM)狄利克雷混合过程分为:嵌套DPMM、关联DPMM、层次DPMM(图 2)。
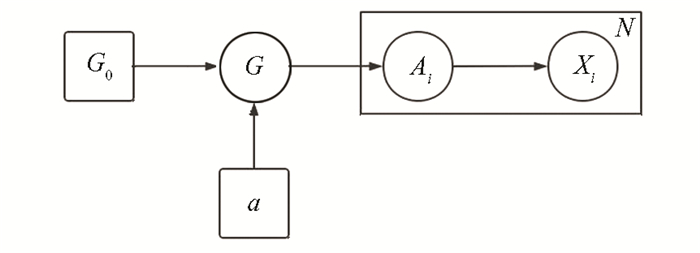
|
图 2 DPMM数学拓扑 Figure 2 DPMM mathematical topology |
从图中可以看出,根据参数α在G0中选出G的过程是DPMM过程,在Ai的条件下不断得试探G到xi,选取过程可以是无限多次。
在共享样本中进行采样,如果该过程符合马尔可夫蒙特卡洛采样法就可以构造为分层DPMM(图 3)。
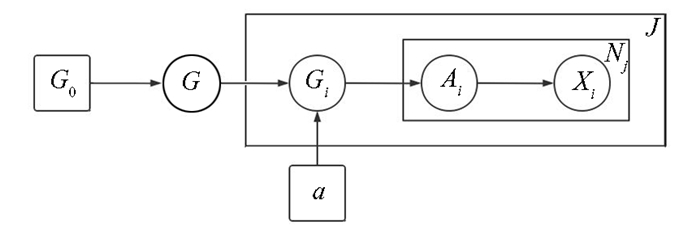
|
图 3 分层DPMM数学拓扑 Figure 3 Hierarchical DPMM mathematical topology |
从图 3中可以看出在G0中选出Gj的过程是分层Dirichlet过程,首先在G0中选出G的但是G的不能满足α的条件,又在G中选出Gj满足α的条件,在Ai的条件下不断得试探Gj到xi,重复选出Gj满足α的条件继续在Ai的条件下不断得试探Gj到xi,知道满足条件J。
既可以通过构造采样函数可以进行DPMM的无限循环过程,也可以通过无线叠加样本进行DPMM的无限循环过程。鉴于实验所用OTUs是有限的,采用抽样函数进行Dirichlet过程,考虑到实现过程中不可能真正无限运行,以样本遍历最大次数为结束无线循环过程的条件。
狄利克雷混合过程下的OTUs数据分类模型前描述,描述结果见图 4,图 5。
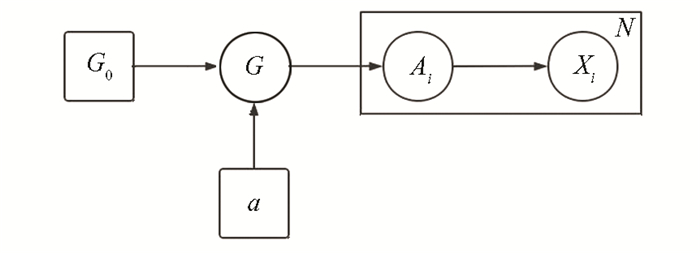
|
图 4 DPMM OTUs数据聚类拓扑 Figure 4 DPMM OTUs data clustering topology |

|
图 5 分层DPMMOTUs数据聚类拓扑 Figure 5 Hierarchical dpmmotus data clustering topology |
从图 4可以看出,此时G0变成OTUs数据集,α是随机采样规则,Ai为聚类过程,xi为聚类结果,N为聚类寻优过程。
从图 5可以看出,此时G0变成OTUs数据集,G部分OTUs数据集,α是随机采样规则,Ai为聚类过程,xi为聚类结果,N为聚类寻优过程,J是K均值的K选取过程。
3 K-means的Dirichlet过程引入Dirichlet过程可以充分解决K均值选择K值难的问题,此处选用分层DPMM。外层通过对K值的变化构建不同的K-means算法,内层通过对数据集采样Dirichlet过程实现。可以看出分层DPMM天生适用于聚类算法的调优。其拓扑结构见图 6。
|
图 6 PDMM改进的K均值数学拓扑图 Figure 6 Improved K-means mathematical topology of PDMM |
构建算法:
1) 采用抽样算法从数据X中抽出样本Xnk,Xnk与X列属性相同;
2) 给K-means设置最大K值;
3) 选择K个样本作为初始的聚类中心On;
| $ O_n=\left\{X_{n i}, X_{n j}, \cdots, X_{n k}\right\}, i \neq j \neq k<K $ | (5) |
4) 针对样本Xnk计算其距离聚类中心距离Dn,并计算代价函数L(Xnk, On),并将距离最小的样本与聚类中心归为一类Cnm;
| $ D_n=\left\{\left\|X_{n k}-O_n\right\|\right\}, i \neq j \neq k<K $ | (6) |
| $ \begin{aligned} & C_{n m}=\left\{\left\{X_n \mid L\left(X_{n k}, O_n\right)=min \left(L\left(X_{n k}, O_n\right)\right)\right\}, \right. \\ & \left.O_n\right\} \end{aligned} $ | (7) |
5) 对每类求算数平均作为新的聚类中心;
| $ O_{n m}=\frac{\sum C_{n m}}{{len}\left(C_{n m}\right)} $ | (8) |
6) 重复2、3步操作,知道代价函数达L到终止条件L0。
改进算法保留了K均值实现容易,收敛速度快,距离效果好,算法解释性强的同时,还解决了K值选择难的问题。
对于n个m维数据分成K类的时间复杂度为O(tKnmNJ),空间复杂度O(m(n+K)NJ)。
4 实验结果与分析K-means算法是一种基于距离的聚类方法,它以k为参数,把包含n个对象的数据集划分为k个簇,使得簇内具有较高的相似度,而簇与簇之间的相似度较低。其基本思想是:根据预先设定的的聚类中心数随机选取K个样本点作为初始聚类中心,把剩余的对象分配给离它最近的簇中;然后将各簇所有对象的平均值作为新的聚类中心,并把每个对象重新分配到最近的簇中,不断迭代该过程,直到聚类质量不再发生变化,目标函数最小化为止。实验结果见表 1,表 2。
| 表 1 实验结果对比 Table 1 Comparison of experimental results |
| 表 2 在Iris数据集上的有效性结果对比 Table 2 Comparison of effectiveness results on Iris dataset |
1) 算法首先计算每个样本点的局部密度和相对距离,将每个样本点的局部密度和相对距离作积,并将其降序排列,然后根据输入的聚类数自动选取前K个决策值较大的样本点作为初始聚类中心点。
2) 将选取的K个聚类中心应用到K-means算法中,并利用各簇的中位数代替原来的均值进行后续聚类中心的更迭。
从表 1中的两个有效性指标来看,改进后的K-means算法的聚类准确性明显优于K-means这是因为K-means算法随机选取初始聚类中心严重影响聚类的准确性和稳定性。在R15数据集上,改进的K-means算法的准确率和标准化互信息高达99%以上,聚类效果与真实情况将近吻合。
表 2给出了改进后的K-means算法与K-means在Iris数据集上的详细情况。两种种算法共运行10次,并给出了每次运行时所选取的初始中心点(用数据集中对应的编号表示)、初始聚类中心所对应的实际类别、迭代次数、运行时间。
从表 2中可以看出,传统的K-means算法每次选取的初始聚类中心都是随机的,导致每次聚类结果不一致;并且在很多情况下,选取的初始聚类中心可能位于同一个簇中,这样使得最初的聚类中心过于邻近,导致算法迭代次数增加。改进后的K-means算法每次运行所选取的初始聚类中心是唯一的,且每个聚类中心点与真实类别相对应,算法具有很好的稳定性。
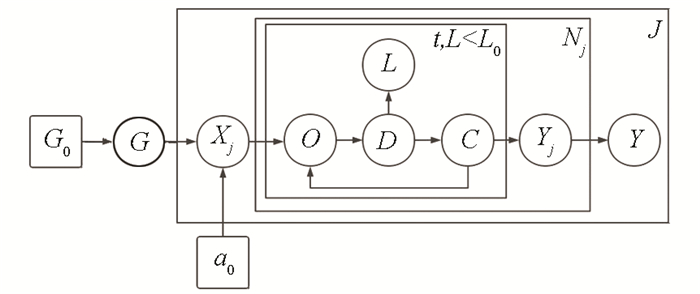
4.2 实验数据集与评价标准实验数据集来源于云南第一人民医院内分泌科在2015年到2017年对2型糖尿病患者统计。其中N为学校正常对照20例,PN为医院正常对照19例,P为2型糖尿病合并胃肠自主神经病变30例,D为2型糖尿病76例。
本文引入了许多信息准则。通过加大模型复杂度的惩罚函数来避免拟合。假设聚类结果有参数k个,观察数n个,测试值为y,中心点值为
1) AIC(赤池信息准则)
AIC由日本赤池弘次在1974年提出的,是衡量模型拟合优良性的一个标准。它的定义是建立在熵的概念上,为模型复杂度和拟合数据优良性的评价提供了标准。具体函数如下:
| $ \mathrm{AI}C=2 k+nln \left(\frac{\sum(y-\tilde{y})^2}{n}\right) $ | (9) |
2) BIC(贝叶斯信息准则)
BIC惩罚考虑了样本数量,对样本数量大,防止模型精度过高而造成模型复杂度过高。BIC于1978年由Schwarz提出,具体公式如下:
| $ \mathrm{BI} C=\mathrm{kl}n(n)+nln \left(\frac{\sum(y-\tilde{y})^2}{n}\right) $ | (10) |
相较于与RMSE(均方根误差)只关注残差,AIC、BIC综合衡量了模型的复杂度与拟合程度。调整R2(Adj-R2)虽然突破了R2解释样本与拟合模型相关系数的局限,但是当参数不断变多时:
| $ \operatorname{Ad}j-R^2=1-\frac{R S S}{T S S} $ | (11) |
其中
本文选择AIC与BIC作为实验评估,并作为实验过程中的惩罚函数。
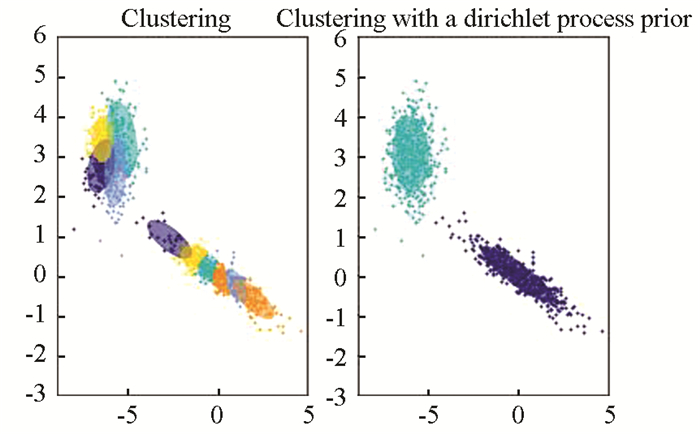
为了反映出模型过拟合的特性,给定5个二维高斯分布,每个分布随机采样500个点,
|
图 7 过拟合实验 Figure 7 Over fitting experiment |
从图 7可以看出传统聚类方法为最求高精度将原始数据分为10个类,但是通过DPMM改进的聚类算法将数据分为2类。主观上看:散点主要集中在两个区,没有必要拟合成10类。此类过拟合是典型的参数太多,模型复杂度过高造成的。进一步评估DPMM改进算法的AIC与BIC见图 8。

|
图 8 模型评价 Figure 8 Model evaluation |
分类越低AIC与BIC越好,因此DPMM改进的聚类算法,会随着参数的增多拟合度更。可以看出,BIC的抬升幅度远大于AIC。两种评估准则第二项相同,造成差异来源于第一项。每一个Dirichlet组成值都是对K均值进行一次聚合。传统的K均值方法无法实现K值由2~10的光滑过渡,但是DPMM改进的K-means算法可以很好的实现。K值由一到极大的某值计算。
4.3 Ⅱ型糖尿病合并胃肠自主神经病变与Ⅱ型糖尿病菌群差异在对OTUs数据进行聚类分析之前,还需要分析一下样本的种类。并且对每类样本进行主成分分析。本实验所用的OTUs数据包含生物种类包括囊括海量细菌与古生菌。16s RNA获得了近2 000种OTU序列,包含2界,OTUs识别率100%;28门,OTUs识别率99.39%;55纲,OTUs识别率97.83%;108目,OTUs识别率95.38%;185科,OTUs识别率85.41%;408科,OTUs识别率62.47%;284种,OTUs识别率16.76%, 见表 3。
| 表 3 生物种类 Table 3 Biological species |
分P、PN、N、D4类分析OTU分布。以85%识别率为主要分析目标,鉴于界的种类只有2种,没有聚类的必要,后续分析将集中在门纲目的级别进行分析与实验。实验以0.001为识别精度。
Ⅱ型糖尿病合并胃肠自主神经病变记为P类,与OTUs关联有效数据有268个,包含生物分类见表 4,表 5。
| 表 4 Ⅱ型糖尿病合并胃肠自主神经病变生物种类 Table 4 Biological species of type Ⅱ diabetes mellitus with gastrointestinal autonomic neuropathy |
| 表 5 Ⅱ型糖尿病生物种类 Table 5 Biological types of type Ⅱ diabetes |
Ⅱ型糖尿病合并胃肠自主神经病变包含9门,占OTUs总门类的32.14%;包括17纲,占OTUs总门类的30.91%;包括17目,占OTUs总目类的15.74%。进一步分析门类发现厚壁菌门(Firmicutes)、拟杆菌门(Bacteroidetes)与变形菌门(Proteobacteria)表现明显。鉴于Firmicutes、Bacteroidetes比例与肥胖有密切关系,作为人体中含量较大的两种分布广泛,Firmicutes是指细胞壁的肽聚糖含量高,一般在50%到80%,全部为化能营养型生物,无光能营养型,琦细胞壁厚度在10~50 nm。Bacteroidetes广泛具有外膜、肽聚糖层和细胞质膜,其中多糖是Bacteroidetes的主要能量来源。Proteobacteria外膜由脂多糖组成,参与人体多种代谢,具有极多形状。
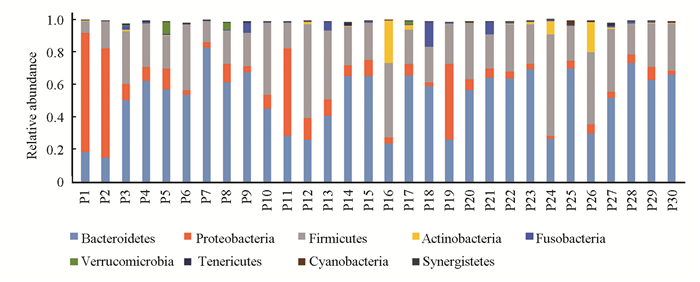
Firmicutes、Bacteroidetes、Proteobacteria是影响Ⅱ型糖尿病的主要门类,见图 9。
|
图 9 Ⅱ型糖尿病合并胃肠自主神经病变纲类中主要细菌的相对丰度分布 Figure 9 Relative abundance distribution of main bacteria in the class of type Ⅱ diabetes mellitus with gastrointestinal autonomic neuropathy |
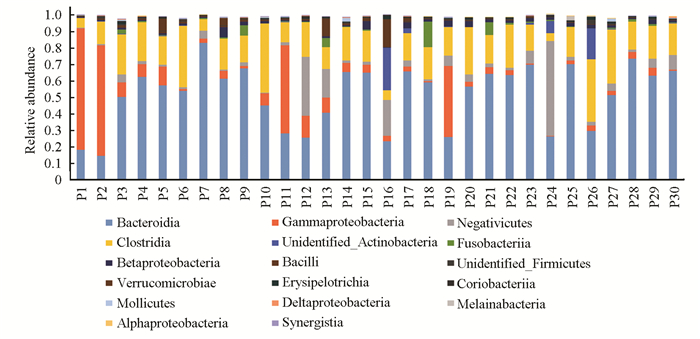
如图 9分析纲类发现,Bacteroidia,Clostridia,Negativicutes与unidentified_Actinobacteria表现明显。拟杆菌纲(Bacteroidia)作为人体肠道中优势厌氧菌,对维持微生态体系具有重要作用。梭菌纲(Clostridia)芽孢直径往往会大于菌体,菌体整体成梭形,其中少数为致病菌。厚壁菌纲(Negativicutes)与放线菌门未确认纲(Unidentified_Actinobacteria)均表现为个体案例占比高,见图 10-图 11。
|
图 10 Ⅱ型糖尿病合并胃肠自主神经病变目类中主要细菌的相对丰度分布 Figure 10 Relative abundance distribution of main bacteria in the order of type Ⅱ diabetes mellitus with gastrointestinal autonomic neuropathy |

|
图 11 Ⅱ型糖尿病合并胃肠自主神经病变科类中主要细菌的相对丰度分布 Figure 11 Relative abundance distribution of main bacteria in the family of type Ⅱ diabetes mellitus with gastrointestinal autonomic neuropathy |
如图 10分析目类发现,Bacteroidales、Clostridiales、Selenomonadales与Bifidobacteriales表现明显,其分别为拟杆菌目、梭菌目、硒单目和双歧杆菌目。
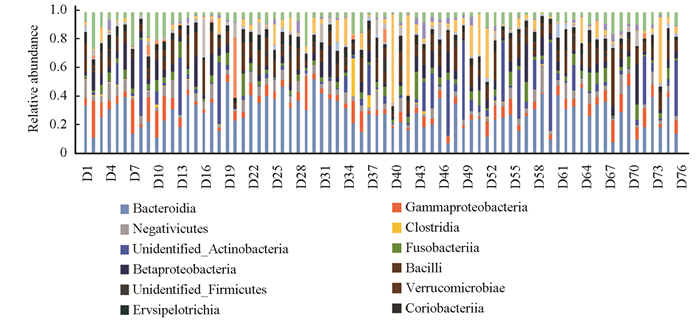
2型糖尿病包含10门,占OTUs总门类的35.71%;19纲,占OTUs总门类的34.55%;20目,目占OTUs总目类的18.52%。详见图 12-图 13。
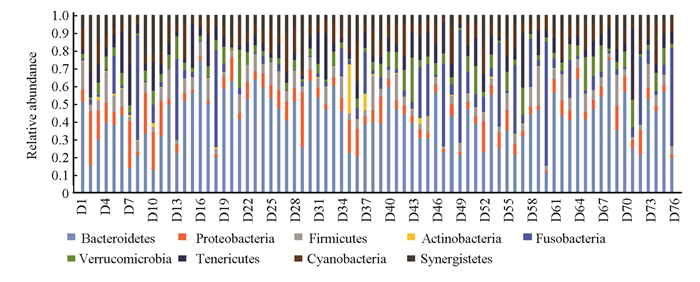
|
图 12 Ⅱ型糖尿病门类中主要细菌的相对丰度分布 Figure 12 Relative abundance distribution of main bacteria in type Ⅱ diabetes |
|
图 13 Ⅱ型糖尿病纲类中主要细菌的相对丰度分布 Figure 13 Relative abundance distribution of main bacteria in type Ⅱ diabetes |
Bacteroidetes、Firmicutes、Proteobacteria、Cyanobacteria、Fusobacteria表现突出与Ⅱ型糖尿病合并胃肠自主神经病变不完全相同。没有减少新的门类,影响Ⅱ型糖尿病的细菌门类包含了影响胃肠自主神经病变的门类。单是缺少了Cyanobacteria、Fusobacteria。蓝菌门(Cyanobacteria)也值得注意, 蓝菌就是旧分类法中的蓝藻门(Cyanophyta)因为细胞生物学研究发现它们属于原核生物, 理论上是一种细菌。梭杆菌门(Fusobacteria)是一个小类群的革兰氏阴性细菌。其中梭杆菌属常见于消化道,是口腔菌群之一,也可导致一些疾病。
Bacteroidia、Chloroplast、Gammaproteobacteria表面明显。Bacteroidia、Chloroplast与Ⅱ型糖尿病合并胃肠自主神经病变相同,单是Gammaproteobacteriaγ变形菌纲是所知的细菌中种类最多的一纲典型代表如沙门氏菌属(肠炎和伤寒)、耶尔辛氏菌属(鼠疫)、弧菌属(霍乱)、绿脓杆菌。
Bacteroidales、Aeromonadales表现明显。Bacteroidales与Ⅱ型糖尿病合并胃肠自主神经病变相同,Aeromonadales为气单胞菌目可引起人类腹泻。
4.4 DPMM混合下聚类分析采用DPMM改进聚合方式对给定K值进行遍历。K值的表达观测数值开始增大,DPMM迭代次数越多,抽样迭代观测量越大。具体流程如下:
1) 导入清晰后OTUs数据,将OTU对所有样本案例相关性均为0数据删除;
2) 判断导入的OTUs数据集一行数据的和是否为0,为0终止程序并报错,不为0继续执行;
3) 通过OTUs对模型进行初始化,并生成符合正态分布的函数;
4) 对OTUs进行抽样;
5) 给定权重,计算抽样拟合结果;
6) 将拟合结果由好到差不断填充到列表中,并按权重加权拟合结果,此权重可以满足无限权重的和为1;
7) 重复4、5、6,直到满足终止条件。
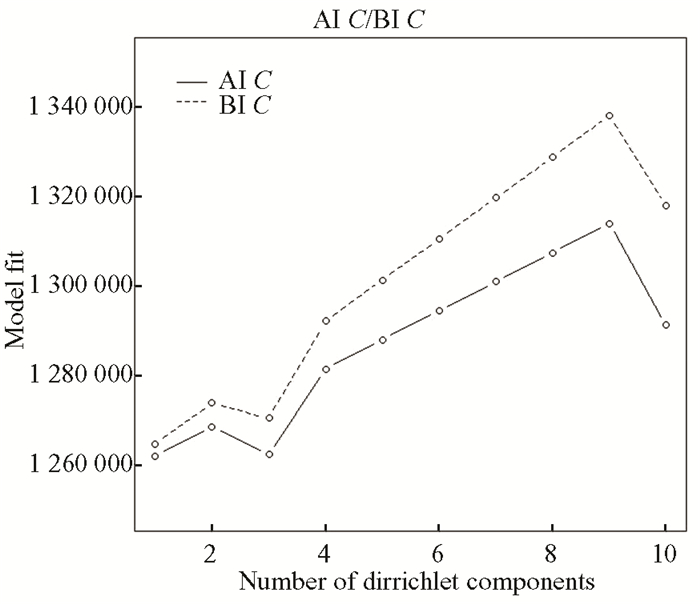
本实验以K-means算法最大聚类10类为终止条件,以AIC/BIC进行评估,反馈聚类的种类个数见图 14。
|
图 14 DPMM混合聚类模型拟合效果 Figure 14 Fitting effect of DPMM mixed clustering model |
根据图 14,首先排除分1类的无意义结果,发现当K=3时,AIC/BIC值最小,所以AIC/BIC最佳,并且AIC与BIC的走势整体一致说明,观察观测参数变化良好。分析每一个OTU的贡献情况贡献最突出的OTU为OTU963、OTU363、OTU1390、OTU19、OTU359分别对应物种种类为:
OTU963k__Bacteria; p__Firmicutes; c__Clostridia; o__Clostridiales
OTU363k__Bacteria; p__Firmicutes; c__Clostridia; o__Clostridiales; f__Ruminococcaceae
OTU139k__Bacteria; p__Proteobacteria; c__Betaproteobacteria; o__Burkholderiales; f__Comamonadaceae; g__Tepidimonas; s_
OTU19k__Bacteria; p__Bacteroidetes; c__Bacteroidia; o__Bacteroidales; f__Bacteroidaceae; g__Bacteroides; s__Bacteroides_caccae
OTU359k__Bacteria; p__Firmicutes; c__Clostridia; o__Clostridiales; f__Clostridiales_vadinBB60_group; g__; s__
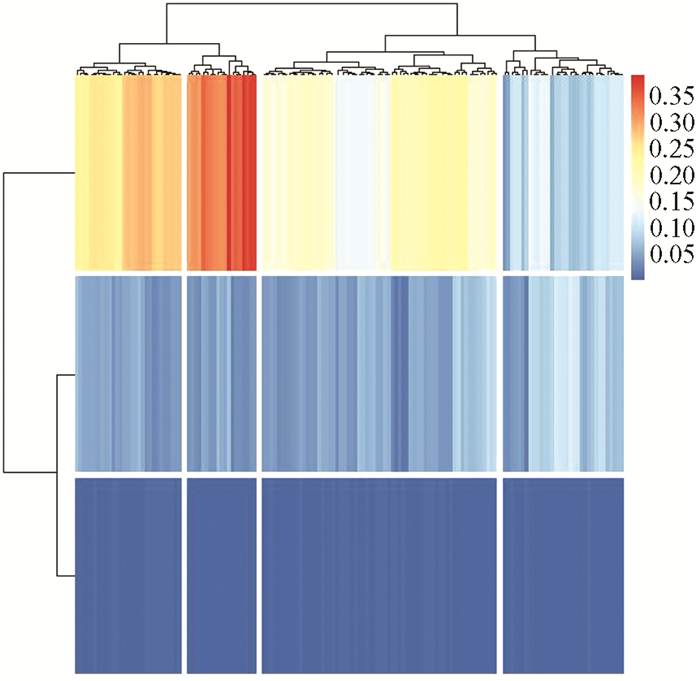
进一步对比DPMM优势,采用热力图分析发,将样本数据分为4类,OTUs用K-means分别聚成2类、4类、1 796类,用DPMM改进的K-means进行聚类,聚类效果见图 15-图 18。

|
图 15 K-means 2聚类热图 Figure 15 K-means 2 clustering heat map |

|
图 16 K-means 4聚类热图 Figure 16 K-means 4 clustering heat map |

|
图 17 K-means 1796聚类热图 Figure 17 K-means 1796 clustering heat map |
|
图 18 PDMM改进K-means聚类热图 Figure 18 PDMM improved K-means clustering heat map |
图 15是将K-means的K值设定为2;图 16是将K-means的K值设定为4;图 17是将K-means的K值设定为1 796,从热力图中可以得出每个OTU的分布情况;图 18是将K-means是运用DPMM+K-means进行结合得出来的,DPMM通过不断选取K值,最后选出了K=3时为最佳,热力图可以看出聚成三类后分层效果明显,得出结果与传统生物信息学分析一致。
综上,运用DPMM+kmeans进行分析时,发现当K=3时,AIC/BIC最佳,并且AIC与BIC的走势整体一致说明,观察观测参数变化良好。采用多层狄利克雷过程与传统生物信息学分析得到的结果一致,研究结果表明,DPMM+K-means模型不仅能够有效地区分2-型糖尿病患者样本间的相似性,而且能从中发现DPMM+K-means模型还能鉴定出影响菌群结构异质性最大的OTUs菌。
5 总结本研究主要是基于狄利克雷过程混合模型与K-means聚类算法结合的2-型糖尿病肠道菌群研究, 通过对肠道菌群OTUs数据进行分析, 建立了一个完整、系统化以及可视化的模型。将分析的结果与传统的生物信息学分析进行对比,发现当K=3时,AIC/BIC最佳,并且AIC与BIC的走势整体一致说明,观察观测参数变化良好。从热力图也可以看出K=3时,第一,二,三类对样本的反映效果更加明显。算法将菌群数据分为三个族,并且能够找出贡献最突出的OTU,具有实际意义,为研究肠道菌群提供了一种新的方法。分析每一个OTU的贡献情况。能够找出贡献最突出的OTU分别为贡献最突出的OTU为OTU963、OTU363、OTU1390、OTU19、OTU359,为进一步对比DPMM优势,采用热力图分析,将样本数据分为4类,对OTUs用K-means分别聚成2类、4类、1 796类,用DPMM改进的K-means进行聚类,得出结果与传统生物信息学分析一致。
| [1] |
HILL-BURNS E M, DEBELIUS J W, MORTON J T, et al. Parkinson's disease and Parkinson's disease medications have distinct signatures of the gut microbiome[J]. Movement Disorders, 2017, 32(5): 739-749. DOI:10.1002/mds.26942 (  0) 0) |
| [2] |
KOREN O, KNIGHTS D, GONZALEZ A, et al. A guide to enterotypes across the human body: meta-analysis of microbial community structures in human microbiome datasets[J]. PLoS Computational Biology, 2013, 9(1): e1002863. DOI:10.1371/journal.pcbi.1002863 (  0) 0) |
| [3] |
HONG B Y, FURTADO ARAUJO M V, STRAUSBAUGH L D, et al. Microbiome profiles in periodontitis in relation to host and disease characteristics[J]. Plos One, 2015, 10(5): e0127077. DOI:10.1371/journal.pone.0127077 (  0) 0) |
| [4] |
HOLMES I, HARRIS K, QUINCE C. Dirichlet multinomial mixtures: generative models for microbial metagenomics[J]. PLoS ONE, 2012, 7(2): e30126. DOI:10.1371/journal.pone.0030126 (  0) 0) |
| [5] |
DONG Mei, LI Longhai, CHEN Man, et al. Predictive analysis methods for human microbiome data with application to Parkinson's disease[J]. PLoS One, 2020, 15(8): e0237779. DOI:10.1371/journal.pone.0237779 (  0) 0) |
| [6] |
CHEN Jun, LI Hongzhe. Variable selection for sparse Dirichlet-multinomial regression with an application to microbiome data analysis[J]. The Annals of Applied Statistics, 2013, 7(1): 418-442. DOI:10.1214/12-AOAS592 (  0) 0) |
| [7] |
YANG Yuqing, WANG Xin, XIE Kaikun, et al. Inferring multiple metagenomic association networks based on variation of environmental factors[J/OL]. https://www.biorxiv.org/content/10.1101/2020.03.04.976423v1, 2020. DOI: 10.1101/2020/03.04.976423.
(  0) 0) |
| [8] |
SHI Yushu, ZHANG Liangliang, DO K A, et al. Bayesian approaches for flexible and informative clustering of microbiome data[J/OL]. https://arxiv.org/abs/2007.15812.2020. DOI: 10.48550/arXiv.2007.15812.
(  0) 0) |
| [9] |
IRANNIA Z B, CHEN T. TACO: Taxonomic prediction of unknown OTUs through OTU co-abundance networks[J]. Quantitative Biology, 2016, 4(3): 149-158. DOI:10.1007/s40484-016-0073-2 (  0) 0) |
| [10] |
MAO Jialiang, MA Li. Dirichlet-tree multinomial mixtures for clustering microbiome compositions[J]. The Annals of applied statistics, 2020, 16(3): 1476-1499. DOI:10.48550/arXiv.2008.00400 (  0) 0) |
| [11] |
NICCOLAI E, BALDI S, RICCi F, et al. Evaluation and comparison of short chain fatty acids composition in gut diseases[J]. World Journal of Gastroenterology, 2019, 25(36): 5543-5558. DOI:10.3748/wjg.v25.i36.5543 (  0) 0) |
| [12] |
HARRIS K, PARSONS T L, IJAZ U Z, et al. Linking statistical and ecological theory: Hubbell's unified neutral theory of biodiversity as a hierarchical dirichlet process[J]. Proceedings of the IEEE, 2017, 4(3): 516-529. DOI:10.1109/JPROC.2015.2428213 (  0) 0) |
| [13] |
PENG Y, SHAW C A. An efficient algorithm for accurate computation of the Dirichlet-multinomial log-likelihood function[J]. Bioinformatics, 2014(11): 1547-1554. DOI:10.1093/bioinformatics/btu079 (  0) 0) |
 2024, Vol. 22
2024, Vol. 22


