2. 哈尔滨工业大学 计算机科学与技术学院,哈尔滨 150001
2. School of Computer Science and Technology, Harbin Institute of Technology, Harbin 150001, China
有研究称人体基因组中约12%的区域易于发生拷贝数变异(Copy number variant,CNV);许多复杂疾病如精神分裂[1]、孤独症[2-3]、癌症[4]等,都与其相关。传统的拷贝数变异检测技术有荧光免疫原位杂交(Fluorescence in situ hybridization,FISH)技术、微阵列比较基因组杂交(Array comparative genomic hybridization,aCGH)技术和SNP芯片(Single nucleotide polymorphism Array)技术等[5]。
随着高通量二代基因测序技术的发展,越来越多的研究采用高通量测序技术检测拷贝数变异,截至目前已经有数十种检测拷贝数变异的方法提出。这些方法从总体可以分为:基于reads深度(Read depth,RD)的方法,基于双末端映射(Pair end mapping,PEM)的方法,基于拆分read(Split read,SR)的方法,基于从头拼接(De novo assembly,AS)的方法,以及基于上述四种方法的组合方法。其中,基于reads深度的拷贝数变异检测方法,利用拷贝数变异区域与无拷贝数变异区域的reads深度差异来检测拷贝数变异;基于双末端的拷贝数变异检测方法,利用双末端配对reads在拷贝数变异区域比对之后其方向或者插入片段长度会发生特定变化这一特性来检测拷贝数变异;基于拆分read的拷贝数变异检测方法利用跨越拷贝数变异断点的reads拆分重比对来检测拷贝数变异;基于从头拼接的拷贝数变异检测方法是将全基因组或局部区域的reads从头拼接之后,然后比对到参考基因组来检测拷贝数变异;组合方法综合利用以上策略来进行拷贝数变异的检测。这些检测方法在算法、模型等方面各有优缺点,适用于不同类型、不同长度的拷贝数变异的检测。本文全面地综述目前常用的几种基于高通量测序数据的拷贝数变异检测方法,客观的分析总结已有方法的优缺点,为新的拷贝数变异检测算法奠定基础。
1 基于高通量测序数据的拷贝数变异检测方法目前,基于高通量测序数据的拷贝数变异检测方法主要有四大类:1)基于reads深度(Read depth,RD)的方法;2)基于双末端映射(Pair end mapping,PEM)的方法;3)基于拆分read(Split read,SR)的方法;4)基于从头拼接(De novo assembly,AS)的方法,不同拷贝数变异检测方法对比见表 1。
| 表 1 不同拷贝数变异检测方法的比较 Table 1 Comparision of different copy number variation detection methods |
在人类基因组中的常染色体上,没有发生拷贝数变异的正常区域的任何序列片段都对应2个拷贝;而拷贝数变异区域的序列片段或少于2个拷贝(发生“删除”变异),或多于2个拷贝(发生“重复”变异)。因此,同样长度的基因组区域,拷贝数变异区域和正常区域测序得到的reads数量(即reads深度)也会有明显差异。由于整个基因组区域中拷贝数变异区域只占很小一部分,整个基因组总体平均的reads深度和拷贝数变异区域会有明显的差异。基于reads深度的拷贝数变异检测方法是通过查询reads深度异常的区域来检测不同类型的拷贝数变异。基于reads深度的拷贝数变异检测方法的示意图见图 1。
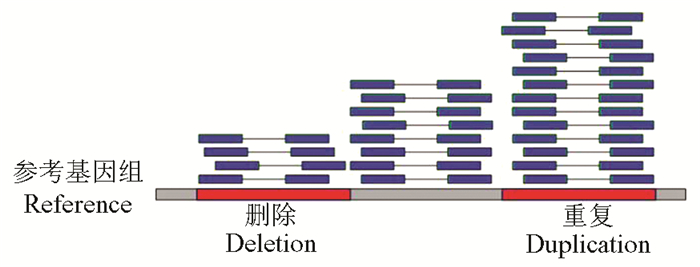
|
图 1 基于reads深度的拷贝数变异检测方法示意图 Figure 1 Schematic illustration of read depth-based copy number variation detection approaches |
基于reads深度的拷贝数变异检测方法通常包含两大关键步骤:1)reads深度的标准化(Normalization)与概率建模;2)拷贝数变异区域的分割(Segmentation)。
在二代测序数据中,基于reads深度的拷贝数变异检测方法通常首先将基因组划分成连续的小窗口(重叠的或者非重叠的),然后计算每个窗口的reads深度,即起始点在窗口内的reads总数。全基因组测序数据划分的窗口通常为固定长度,可以直接指定窗口尺寸,也可以根据不同的测序数据集采用基于模型的方法估算出最优的窗口尺寸。
在基因组的某些区域,reads深度异常可能是由拷贝数变异引起的,也可能是由于测序和reads比对过程中的其他因素引起的偏差。GC含量和mappability是其中两个影响最大的因素。reads深度的标准化是指通过GC含量校正和mappability校正,消除其引起的偏差,使得基因组特定区域的异常reads深度能够真实地反映拷贝数变异。目前相对成熟的拷贝数变异检测方法绝大多数考虑了GC含量校正和mappability校正的问题。
Yoon等[6]提出的基于中位数归一化的GC含量校正方法见公式(1)。其中ri表示GC含量校正前某一窗口的reads深度,
| $ \tilde{r}_i=r_i \cdot \frac{m}{m_{G C}} $ | (1) |
| $ \tilde{r}_i=r_i \cdot \frac{m}{m_{M A P}} $ | (2) |
另外一种常用的GC含量校正方法基于局部加权回归散点平滑法(Locally weighted scatterplot smoothing,LOWESS或LOESS)[7]。
在reads深度的标准化的同时或之后是构建reads深度的概率模型,即以某种特定的概率分布(通常是不同参数下的混合概率分布)来拟合真实测序数据的reads深度,现在常用的reads深度概率模型有高斯分布、泊松分布和负二项分布等,和在上述基本概率分布的基础上引入其余影响reads深度分布的协变量。
reads深度的标准化与概率建模的下一步是进行拷贝数变异区域的分割。拷贝数变异区域的分割是指基于reads深度概率模型和不同分割方法识别全基因组的拷贝数变异的具体区域。迄今为止,大量的拷贝数变异区域的分割方法被提出,其中,CNVnator[8]利用基于均值偏移(Mean shift-based, MSB)的方法;RDXplorer[6]利用基于EWT(Event-wise testing)的方法;JointSLM[9]利用基于SLM(Shifting level model)的方法;ReadDepth[10]利用基于循环二元分割(Circular binary segmentation,CBS)的方法;GENSENG[11]和CNVwire[12]利用基于隐马尔可夫模型(Hidden markov model,HMM)的方法。CNVnator[8]是一种较为经典的基于reads深度的方法,该方法在比对之后,首先将基因组划分为等长窗口,计算每个窗口内的reads深度,但计算reads深度时需要利用GC含量校正原始的reads深度;然后,CNVnator使用mean-shift算法[13],利用校正之后的reads深度值,对邻近的bin进行聚类,理论上聚为一类的bin具有相同的拷贝数,上述的聚类信号只有在染色体的局部具有意义;再次,在全基因组范围来识别CNV时,通过segmentation算法来实现,不同的bandwidth参数取值影响到拷贝数变异区域的划分;最后,CNVnator的bin和bandwidth两个参数的选择对结果影响很大。
1.2 基于双末端映射的拷贝数变异检测方法双末端测序是指从一个DNA片段的两个5’端同时展开,生成双末端reads,双末端reads两个5’端之间的距离为插入片段长度(Insert size),双末端reads的示意图如图 2所示。双末端reads的插入片段的长度与具体的测序文库有关,一般认为插入片段长度近似地服从高斯分布。在基因组的正常区域(无结构变异)内,双末端reads在映射到参考基因组之后插入片段的长度基本保持不变且方向为正反向(上游read为正向、下游read为反向)。在基因组的结构变异区域内,由于受到结构变异的影响,双末端reads在映射到参考基因组之后其插入片段的长度或者双末端reads的方向会根据具体的结构变异的类型发生不同的变化,这样的双末端reads称之为异常reads对(Discordant read pair)。不同形式的异常reads对可反映不同类型的结构变异。
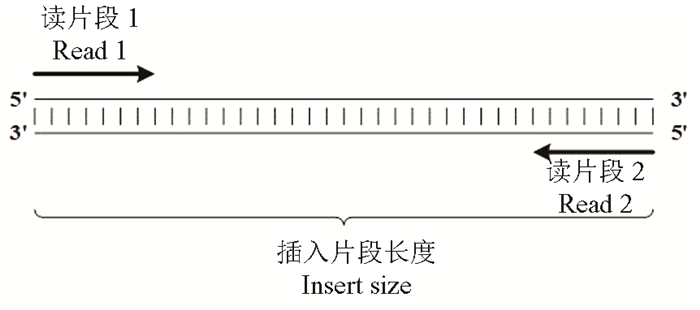
|
图 2 双末端reads示意图 Figure 2 Schematic illustration of paired-end reads |
基于双末端映射的拷贝数变异检测方法即通过异常reads对进行拷贝数变异检测。反映拷贝数变异的异常reads对的示意图见图 3。对于“删除”变异,双末端reads在映射之后其方向保持正反向,但插入片段长度会明显增长,通常设定长度阈值为μ+3σ,其中μ为某一测序文库的插入片段长度的均值(或中位数),σ为插入片段长度的标准差。对于“串联重复”变异,双末端reads在映射之后其方向会发生改变(插入片段长度也可能发生微小的改变)。基于双末端映射的拷贝数变异检测方法首先需要估计每个测序文库产生的双末端reads的插入片段长度的均值和标准差,然后从reads比对数据中提取所有的异常reads对。
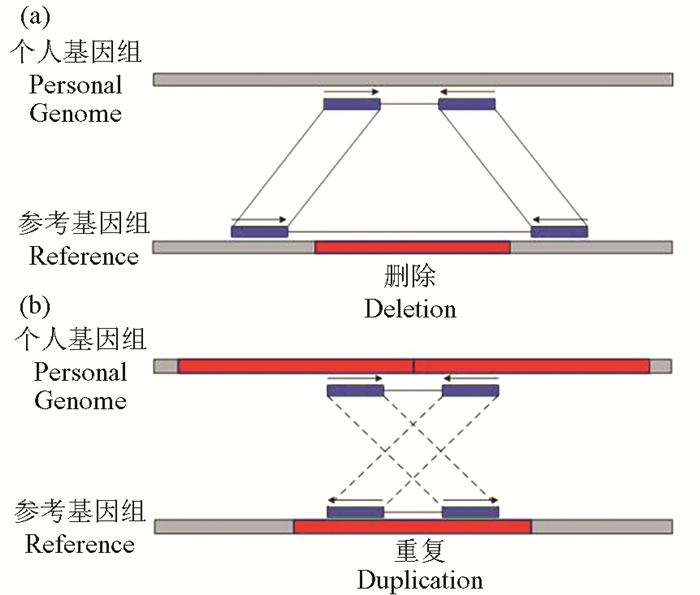
|
图 3 基于双末端映射的拷贝数变异检测方法示意图 Figure 3 Schematic illustration of paired end mapping-basedcopy number variation detection approaches |
由于现有的reads比对方法普遍存在错误,尤其是在基因组的重复区域或一些其他复杂区域,异常reads对可能是比对错误造成的,并不是真实的拷贝数变异的反映。基于双末端映射的拷贝数变异检测方法并不是通过单个异常reads对来判断拷贝数变异,而是将同一区域多个异常reads对聚类,通过这个“类(Cluster)”来判断拷贝数变异。因此,基于双末端映射的拷贝数变异检测方法的核心是对基因组中出现的所有异常reads对进行聚类,使得形成的每一个异常reads对的类均支持某一个具体的拷贝数变异。完成异常reads对的聚类后,通常有两种方法进行拷贝数变异检测,一种是直接利用启发式方法(例如限定至少包含2个异常reads对的类支持一个拷贝数变异)进行检测,另外一种是通过基于模型的方法。目前具有代表性的基于双末端映射的拷贝数变异检测方法有BreakDancer[14]、PEMer[15]、GASV[16]等。
BreakDancer[14]是一款经典的基于PR算法分析拷贝数变异的软件,首先是提取比对文件的配对序列插入片和映射方向异常的序列,然后根据Kolmogorov-Smirnov算法[17]统计分析比对异常区域检测插入、缺失等染色体结构变异。通过如上原理BreakDancer[13]可以检测序列删除、序列插入、序列倒置、染色体内部和染色体之间的易位、序列串联重复/倍增和序列在基因组上的散在重复。BreakDancer[14]的缺点有如下两点:第一,对于缺失的检测,由于要求插入片段长度的变化要具有统计意义上的显著性,所以它所能检测到的片段长度就会受插入片段长度的标准差(SD)所影响。对于大长度缺失(通常是大于1 kbp)比较敏感,准确性也高,而50-200 bp的这个范围内的变异,由于基本还处于2倍标准差以内,在统计检验上它的变化就显得不那么显著,所以这通常就成了它的一个检测暗区。第二,它所能检测的插入序列,长度无法超过插入片段的长度。
1.3 基于拆分read的拷贝数变异检测方法基于拆分read的拷贝数变异检测方法的主要思想是:如果双末端reads中的一条read能够正确映射到参考基因组,而另一条read无法正确映射或只能部分正确映射,则该条无法正确映射的read可能覆盖拷贝数变异(或其余类型的结构变异)的断点(Breakpoint)。若在该条read上找到合适的位置拆分成多段且首尾两段均能够映射到参考基因组,则该条read可以支持一个拷贝数变异(或其余类型的结构变异)。对于“删除”变异和“串联重复”变异的拆分read映射情况示意图见图 4。若一个断点处有多条拆分reads支持同一类型拷贝数变异,则可以确定该断点存在此种类型的拷贝数变异。目前具有代表性的基于拆分read的拷贝数变异检测方法有Pindel [18]、PRISM [19]和AGE[20],其中,Pindel [18]利用模式增长(Pattern growth)的方法进行拆分read的映射;PRISM利用Needleman-Wunsch算法[21]的改进形式来进行拆分read的映射;AGE利用Gap切除的比对方法进行拆分read的映射。Pindel [18]是一种较为经典的基于双末端映射的方法。首先,在获得了单端唯一比对到基因组上的PE read之后,Pindel [18]会将不能正常比对的那条read切开成2或者3小段。然后按照设置的最大deletion长度重新进行比对,并获得最终的比对位置和比对方向,而断点位置的确定就根据soft-clipped的结果来获得。Pindel [18]理论上能够检测所有长度范围内的缺失以及小片段的插入(<50 bp),倒位,串联重复和大片段插入。
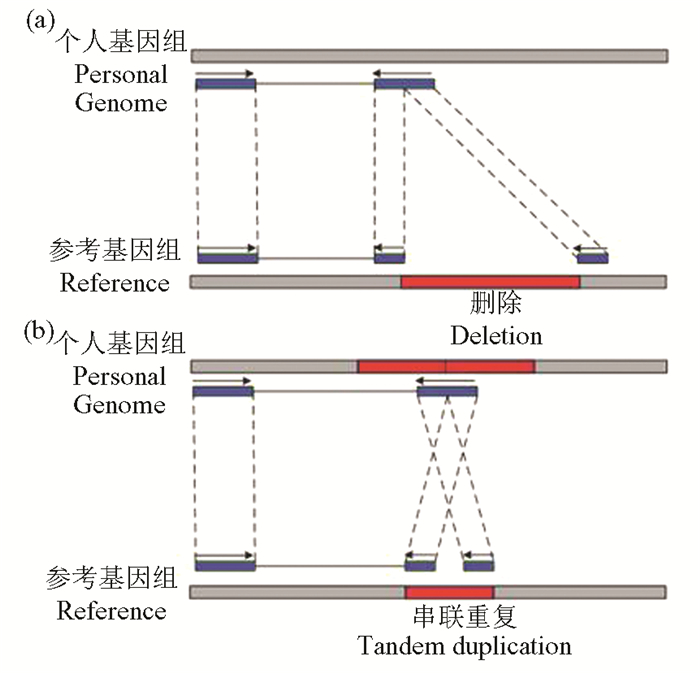
|
图 4 基于拆分read的拷贝数变异检测方法示意图 Figure 4 Schematic illustration of split read-based copy number variation detection approaches |
以上三种拷贝数变异检测方法依赖于reads比对信息,基于从头拼接的拷贝数变异检测方法则不同,不是将reads映射到参考基因组,而是首先对reads进行从头拼接,产生长序列片段(Contigs或Scaffolds),然后将长序列片段映射到参考基因组,从而检测不同类型的拷贝数变异。
理论上常用的从头拼接方法如SOAPdenovo[22]、ABySS[23]和ALLPATHS-LG[24]等均可用于拷贝数变异检测;此外,还有专门基于从头拼接的拷贝数变异检测方法,如SOAPsv[25]、Cortex[26]和FermiKit[27]。但由于高通量测序产生的reads长度较短、错误率高以及人类基因组固有的复杂性(包含大量重复序列)等因素的影响,目前的从头拼接方法对于人类基因组的高通量测序数据的拼接效果并不理想,拼接产生的序列长度较短,且存在一定程度的错误,因而会严重影响拷贝数变异检测的准确率。此外,目前的从头拼接算法均基于图论,时间复杂度和空间复杂度均较高,计算代价极大。此外,对基因组局部区域的reads进行从头拼接可以确定拷贝数变异的断点。例如,TIGRA[28]可以对他方法检测出的拷贝数变异的断点附近的reads进行从头拼接,从而确定拷贝数变异精确的断点。
由于以上4种方法均是利用拷贝数变异反映在测序数据上的某一方面的特征来进行检测,因此每种方法一般只对某些特定类型或特定长度范围的拷贝数变异准确率较高,而对其他类型或长度范围的拷贝数变异的准确率较低。一般来说,基于reads深度的方法适用于长度较长的拷贝数变异,且适用于低覆盖度的测序数据,但提供拷贝数变异断点的分辨率较低;基于双末端映射的方法适用于中等长度的拷贝数变异,且只适用于双末端测序数据,且同样不能够提供单碱基的拷贝数变异断点分辨率;基于拆分read的方法与基于从头拼接的方法适用于长度较短的拷贝数变异,且与上述两种方法不同的是能够提供单碱基的拷贝数变异断点分辨率,基于从头拼接的方法通常需要较高的计算代价。
结合不同方法的优点开发组合方法,能够最大程度地提高对全基因组所有类型、所有长度范围的拷贝数变异的准确率。不同组合方法的组合策略有很大差异。CNVer[29]、ERDS[30]和GASVPro[31]基于reads深度和双末端映射进行拷贝数变异的检测;Delly[32]等基于双末端映射和拆分read进行拷贝数变异检测;HYDRA[33]、SVSeq[34]基于双末端映射和从头拼接进行拷贝数变异检测;cnvHiTSeq[35]和LUMPY[36]基于reads深度、双末端映射和拆分read进行拷贝数变异检测。上述组合方法均可达到比利用单一信息的拷贝数变异检测方法更高的准确率。
4种基本方法均是利用拷贝数变异反映在测序数据上的某些特征来进行拷贝数变异检测。针对家系基因组测序数据,已有的方法没有考虑到具有遗传关系的不同个体间拷贝数变异应该具有的关系。拷贝数变异的来源可以分为两种:新突变和遗传。由于发生新突变的概率极低,一般可以认为不符合孟德尔遗传定律的拷贝数变异是错误的,而符合孟德尔遗传定律的拷贝数变异具有较高的可靠性[37]。目前针对家系基因组测序数据,具有代表性的结合孟德尔遗传定律的拷贝数变异检测方法有Canvas SPW[38]、TrioCNV[39]、MDTS[40]、PennCNV[41-42]、TrioCNV2[43]等。结合孟德尔遗传定律的拷贝数变异检测方法通常呈现出更高的准确率和较低的假阳性率。
通过从拷贝数变异附近的reads比对数据中抽取不同的特征,包括reads深度信息、双末端映射信号、拆分read信息等,通过建立机器学习分类模型,用确定真假的拷贝数变异集合进行训练,然后对4种基本方法产生的拷贝数变异信号进行筛选,可以有效过滤错误的拷贝数变异。目前具有代表性的应用机器学习分类模型的拷贝数变异检测方法有forestSV[44]、SV2[45]、DeepVariant[46]、CNNScoreVariants[47]、Clairvoyante[48]等。应用机器学习进行拷贝数变异检测能够在不损失灵敏度的前提下显著降低假阳性率。
2 拷贝数变异检测存在的主要问题虽然上述不同类别的大量的拷贝数变异检测方法被提出,但总体上已有方法的检测准确率仍然较低。基于reads深度的拷贝数变异检测方法适用于“删除”、“重复”(包括“串联重复”和“散落重复”)变异,而且能够得到具体的拷贝数,但无法确定单碱基分辨率的断点;基于reads深度的拷贝数变异检测方法更适用于长度较长的拷贝数变异,同时也是唯一适合对低覆盖度的全基因组数据以及外显子组测序数据进行拷贝数变异检测的方法。基于双末端映射的拷贝数变异检测方法理论上同样适用于“删除”和包括“串联重复”、“散落重复”在内的“重复”变异,但对“散落重复”的检测效果较差;基于双末端映射的拷贝数变异检测方法适用于中等长度的拷贝数变异,对于断点可提供比基于reads深度的拷贝数变异检测方法更高的分辨率。基于拆分read的拷贝数变异检测方法适用于“删除”变异,尤其是长度较短的“删除”变异。基于从头拼接的方法在基因组的重复区域检测效果较差,同时计算代价极高。基于拆分read的方法和基于从头拼接的方法适用于长度较短的拷贝数变异,且均可提供单碱基的断点分辨率。理论上,结合不同方法优势的组合方法能够最大程度地提高对全基因组所有类型、所有长度范围的拷贝数变异的准确率,已有的研究结果也表明组合方法具有最高的检测准确率。结合孟德尔遗传定律的方法要求必须是应用于家系数据;结合机器学习的方法,其效果依赖于训练集的质量。孟德尔遗传定律和机器学习的应用,能够在几乎不损失灵敏度的前提下,显著降低假阳性率。
3 结束语基于高通量测序数据的基因组拷贝数变异检测目前广泛地应用于基础研究与临床诊疗之中,由于测序技术的局限以及人类基因组自身的复杂性,基于高通量测序数据的拷贝数变异检测方法一直是计算机科学和生物信息学领域的热点与难点问题。本文对基于高通量测序数据的拷贝数变异检测方法的研究进展进行了系统的全面综述,包括基于reads深度的方法、基于双末端映射的方法、基于拆分read的方法、基于从头拼接的方法以及基于上述4种方法的组合方法等。结果表明每种检测方法均有其适用的数据类型,以及各自的优缺点,如何结合不同方法的优缺点开发更新的组合方法,能够有效提升拷贝数变异检测的准确率,但同时也是设计拷贝数变异检测算法或模型的难点,是拷贝数变异检测方法未来的发展方向;此外,随着测序数据规模的不断增长,越来越多的拷贝数变异被发现,基于机器学习的拷贝数变异检测方法将在未来展现出其优势。
为了能够更准确的检测拷贝数变异,需要在数据和算法进行改进。在数据方面,需要制定拷贝数变异的“金标准”数据,因为目前大量检测拷贝数变异的工具的评估和基准测试,需要金标准数据进行评估;在算法上,目前大多数可用的拷贝数变异检测算法的主要问题之一是错误率比较高。可以通过采用机器学习的方法来解决,即将从单个拷贝数变异结果合并到最终的预测中,并通过从示例数据中学习来进行训练。另外一种方法采用长片段测序的方法减少误差,因为三代重测序可直接跨越大片段结构变异;可直接跨越串联重复区域、高GC区域、高度同源区域、高度多态性区域)、无需PCR扩增(避免PCR扩增引入的错误等优势),可以对拷贝数变异检测提供全新策略。
| [1] |
ALKAN C, COE B P, EICHLER E E. Genome structural variation discovery and genotyping[J]. Nature Reviews Genetics, 2011, 12(5): 363-376. DOI:10.1038/nrg2958 (  0) 0) |
| [2] |
GILISSEN C, HEHIR-KWA J Y, THUNG D T, et al. Genome sequencing identifies major causes of severe intellectual disability[J]. Nature, 2014, 511(7509): 344-347. DOI:10.1038/nature13394 (  0) 0) |
| [3] |
DAN L, RONEMUS M, YAMROM B, et al. Rare de novo and transmitted copy-number variation in autistic spectrum disorders[J]. Neuron, 2011, 70(5): 886-897. DOI:10.1016/j.neuron.2011.05.015 (  0) 0) |
| [4] |
BEROUKHIM R, MERMEL C H, PORTER D, et al. The landscape of somatic copy-number alteration across human cancers[J]. Nature, 2010, 463(7283): 899-905. DOI:10.1038/nature08822 (  0) 0) |
| [5] |
COOK J R E H, SCHERER S W. Copy-number variations associated with neuropsychiatric conditions[J]. Nature, 2008, 455(7215): 919-923. DOI:10.1038/nature07458 (  0) 0) |
| [6] |
YOON S, XUAN Z, MAKAROV V, et al. Sensitive and accurate detection of copy number variants using read depth of coverage[J]. Genome Research, 2009, 19(9): 1586-1592. DOI:10.1101/gr.092981.109 (  0) 0) |
| [7] |
BENJAMINI Y, SPEED T P. Summarizing and correcting the GC content bias in high-throughput sequencing[J]. Nucleic Acids Research, 2012, 40(10): e72. DOI:10.1093/nar/gks001 (  0) 0) |
| [8] |
ABYZOV A, URBAN A E, SNYDER M, et al. CNVnator: An approach to discover, genotype, and characterize typical and atypical CNVs from family and population genome sequencing[J]. Genome Research, 2011, 21(6): 974-984. DOI:10.1101/gr.114876.110 (  0) 0) |
| [9] |
MAGI A, BENELLI M, YOON S, et al. Detecting common copy number variants in high-throughput sequencing data by using JointSLM algorithm[J]. Nucleic Acids Research, 2011, 39(10): e65. DOI:10.1093/nar/gkr068 (  0) 0) |
| [10] |
MILLER C A, HAMPTON O, COARFA C, et al. Readdepth: A parallel R package for detecting copy number alterations from short sequencing reads[J]. PloS One, 2011, 6(1): e16327. DOI:10.1371/journal.pone.0016327 (  0) 0) |
| [11] |
SZATKIEWICZ J P, WANG W, SULLIVAN P F, et al. Improving detection of copy-number variation by simultaneous bias correction and read-depth segmentation[J]. Nucleic Acids Research, 2013, 41(3): 1519-1532. DOI:10.1093/nar/gks1363 (  0) 0) |
| [12] |
MCCALLUM K J, WANG J P. Quantifying copy number variations using a hidden Markov model with inhomogeneous emission distributions[J]. Biostatistics, 2013, 14(3): 600-611. DOI:10.1093/biostatistics/kxt003 (  0) 0) |
| [13] |
COMANICIU D, MEER P. Mean shift: A robust approach toward feature space analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619. DOI:10.1109/34.1000236 (  0) 0) |
| [14] |
CHEN K, WALLIS J W, MCLELLAN M D, et al. BreakDancer: An algorithm for high-resolution mapping of genomic structural variation[J]. Nature Methods, 2009, 6(9): 677-681. DOI:10.1038/nmeth.1363 (  0) 0) |
| [15] |
KORBEL J O, ABYZOV A, MU X J, et al. PEMer: A computational framework with simulation-based error models for inferring genomic structural variants from massive paired-end sequencing data[J]. Genome Biology, 2009, 10(2): R23. DOI:10.1186/gb-2009-10-2-r23 (  0) 0) |
| [16] |
SINDI S, HELMAN E, BASHIR A, et al. A geometric approach for classification and comparison of structural variants[J]. Bioinformatics, 2009, 25(12): 222-230. DOI:10.1093/bioinformatics/btp208 (  0) 0) |
| [17] |
DREZNER Z, TUREL O, ZEROM D. A modified kolmogorov-smirnov test for normality[J]. Communications in Statistics-Simulation and Computation, 2010, 39(4): 693-704. DOI:10.1080/03610911003615816 (  0) 0) |
| [18] |
YE K, SCHULZ M H, LONG Q, et al. Pindel: A pattern growth approach to detect break points of large deletions and medium sized insertions from paired-end short reads[J]. Bioinformatics, 2009, 25(21): 2865-2871. DOI:10.1093/bioinformatics/btp394 (  0) 0) |
| [19] |
JIANG Y, WANG Y, BRUDNO M. PRISM: Pair-read informed split-read mapping for base-pair level detection of insertion, deletion and structural variants[J]. Bioinformatics, 2012, 28(20): 2576-2583. DOI:10.1093/bioinformatics/bts484 (  0) 0) |
| [20] |
ABYZOV A, GERSTEIN M. AGE: Defining breakpoints of genomic structural variants at single-nucleotide resolution, through optimal alignments with gap excision[J]. Bioinformatics, 2011, 27(5): 595-603. DOI:10.1093/bioinformatics/btq713 (  0) 0) |
| [21] |
NEEDLEMAN S B, WUNSCH C D. A general method applicable to the search for similarities in the amino acid sequence of two proteins[J]. Journal of Molecular Biology, 1970, 48(3): 443-453. DOI:10.1016/0022-2836(70)90057-4 (  0) 0) |
| [22] |
LI R, ZHU H, RUAN J, et al. De novo assembly of human genomes with massively parallel short read sequencing[J]. Genome Research, 2010, 20(2): 265-272. DOI:10.1101/gr.097261.109 (  0) 0) |
| [23] |
SIMPSON J T, WONG K, JACKMAN S D, et al. ABySS: A parallel assembler for short read sequence data[J]. Genome Research, 2009, 19(6): 1117-1123. DOI:10.1101/gr.089532.108 (  0) 0) |
| [24] |
GNERRE S, MACCALLUM I, PRZYBYLSKI D, et al. High-quality draft assemblies of mammalian genomes from massively parallel sequence data[J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(4): 1513-1518. DOI:10.1073/pnas.1017351108 (  0) 0) |
| [25] |
LI Y, ZHENG H, LUO R, et al. Structural variation in two human genomes mapped at single-nucleotide resolution by whole genome de novo assembly[J]. Nature Biotechnology, 2011, 29(8): 723-730. DOI:10.1038/nbt.1904 (  0) 0) |
| [26] |
IQBAL Z, CACCAMO M, TURNER I, et al. De novo assembly and genotyping of variants using colored de Bruijn graphs[J]. Nature Genetics, 2012, 44(2): 226-232. DOI:10.1038/ng.1028 (  0) 0) |
| [27] |
LI Heng. FermiKit: Assembly-based variant calling for Illumina resequencing data[J]. Bioinformatics, 2015, 31(22): 3694-3696. DOI:10.1093/bioinformatics/btv440 (  0) 0) |
| [28] |
CHEN K, CHEN L, FAN X, et al. TIGRA: A targeted iterative graph routing assembler for breakpoint assembly[J]. Genome Research, 2014, 24(2): 310-317. DOI:10.1101/gr.162883.113 (  0) 0) |
| [29] |
MEDVEDEV P, FIUME M, DZAMBA M, et al. Detecting copy number variation with mated short reads[J]. Genome Research, 2010, 20(11): 1613-1622. DOI:10.1101/gr.106344.110 (  0) 0) |
| [30] |
ZHU M F, NEED A C, HAN Y J, et al. Using ERDS to infer copy-number variants in high-coverage genomes[J]. American Journal of Human Genetics, 2012, 91(3): 408-421. DOI:10.1016/j.ajhg.2012.07.004 (  0) 0) |
| [31] |
SINDI S S, ONAL S, PENG L C, et al. An integrative probabilistic model for identification of structural variation in sequencing data[J]. Genome Biology, 2012, 13(3): R22. DOI:10.1186/gb-2012-13-3-r22 (  0) 0) |
| [32] |
RAUSCH T, ZICHNER T, SCHLATTL A, et al. DELLY: Structural variant discovery by integrated paired-end and split-read analysis[J]. Bioinformatics, 2012, 28(18): i333-i339. DOI:10.1093/bioinformatics/bts378 (  0) 0) |
| [33] |
QUINLAN A R, CLARK R A, SOKOLOVA S, et al. Genome-wide mapping and assembly of structural variant breakpoints in the mouse genome[J]. Genome Research, 2010, 20(5): 623-635. DOI:10.1101/gr.102970.109 (  0) 0) |
| [34] |
ZHANG J, WU Y. SVseq: An approach for detecting exact breakpoints of deletions with low-coverage sequence data[J]. Bioinformatics, 2011, 27(23): 3228-3234. DOI:10.1093/bioinformatics/btr563 (  0) 0) |
| [35] |
BELLOS E, JOHNSON M R, COIN L J. cnvHiTSeq: Integrative models for high-resolution copy number variation detection and genotyping using population sequencing data[J]. Genome Biology, 2012, 13(12): R120. DOI:10.1186/gb-2012-13-12-r120 (  0) 0) |
| [36] |
LAYER R M, CHIANG C, QUINLAN A R, et al. LUMPY: A probabilistic framework for structural variant discovery[J]. Genome Biology, 2014, 15(6): R84. DOI:10.1186/gb-2014-15-6-r84 (  0) 0) |
| [37] |
VELTMAN J A, BRUNNER H G. De novo mutations in human genetic disease[J]. Nature Reviews Genetics, 2012, 13: 565-575. DOI:10.1038/nrg3241 (  0) 0) |
| [38] |
IVAKHNO S, ROLLER E, COLOMBO C, et al. Canvas SPW: Calling de novo copy number variants in pedigrees[J]. Bioinformatics, 2018, 34: 516-518. DOI:10.1093/bioinformatics/btx618 (  0) 0) |
| [39] |
LIU Y, LIU J, LU J, et al. Joint detection of copy number variations in parent-offspring trios[J]. Bioinformatics, 2016, 32: 1130-1137. DOI:10.1093/bioinformatics/btv707 (  0) 0) |
| [40] |
FU J M, LESLIE E J, SCOTT A F, et al. Detection of de novo copy number deletions from targeted sequencing of trios[J]. Bioinformatics, 2019, 35: 571-578. DOI:10.1093/bioinformatics/bty677 (  0) 0) |
| [41] |
WANG K, CHEN Z, TADESSE M G, et al. Modeling genetic inheritance of copy number variations[J]. Nucleic Acids Research, 2008, 36: e138. DOI:10.1093/nar/gkn641 (  0) 0) |
| [42] |
WANG K, LI M, HADLEY D, et al. PennCNV: An integrated hidden Markov model designed for high-resolution copy number variation detection in whole-genome SNP genotyping data[J]. Genome Research, 2007, 17: 1665-1674. DOI:10.1101/gr.6861907 (  0) 0) |
| [43] |
LIU Y, WU X, WANG Y. An integrated approach for copy number variation discovery in parent-offspring trios[J]. Briefings in Bioinformatics, 2021, 22(4): 1-9. DOI:10.1093/bib/bbab230 (  0) 0) |
| [44] |
MICHAELSON J J, SEBAT J. forestSV: Structural variant discovery through statistical learning[J]. Nature Methods, 2012, 9: 819-921. DOI:10.1038/nmeth.2085 (  0) 0) |
| [45] |
ANTAKI D, BRANDLER W M, SEBAT J. SV2: Accurate structural variation genotyping and de novo mutation detection from whole genomes[J]. Bioinformatics, 2018, 34: 1774-777. DOI:10.1093/bioinformatics/btx813 (  0) 0) |
| [46] |
POPLIN R, CHANG P-C, ALEXANDER D, et al. A universal SNP and small-indel variant caller using deep neural networks[J]. Nature Biotechnology, 2018, 36: 983-987. DOI:10.1038/nbt.4235 (  0) 0) |
| [47] |
FRIEDMAN S, GAUTHIER L, FARJOUN Y, et al. Lean and deep models for more accurate filtering of SNP and INDEL variant calls[J]. Bioinformatics, 2020, 36: 2060-2067. DOI:10.1093/bioinformatics/btz901 (  0) 0) |
| [48] |
LUO R, SEDLAZECK F J, LAM T W, et al. A multi-task convolutional deep neural network for variant calling in single molecule sequencing[J]. Nature Commun, 2019, 10: 998. DOI:10.1038/s41467-019-09025-z (  0) 0) |
 2024, Vol. 22
2024, Vol. 22


