2. 南京邮电大学 地理与生物信息学院,南京 210023;
3. 南京林业大学 经济管理学院,南京 210037
2. School of Geographic and Biologic Information, Nanjing University of Posts and Telecommunications, Nanjing 210023, China;
3. College of Economics and Management, Nanjing Forestry University, Nanjing 210037, China
虚拟筛选作为计算机辅助药物设计的实用技术,在现代药物研发中起着重要作用[1]。虚拟筛选在计算平台上模拟药物筛选的过程,可快速从几十至上百万的小分子化合物(配体)中,筛选出有可能和受体结合的活性化合物,大大降低实际筛选小分子化合物数目,缩短药物研发周期,降低药物研发的成本[2-3]。虚拟筛选的方法可分为基于结构的虚拟筛选和基于配体的虚拟筛选[4]。基于结构的虚拟筛选利用分子对接技术,在已知蛋白质受体的三维结构的基础上,在结合位点处自动匹配化合物数据库中的小分子配体,用打分函数对可能的结合模式进行能量计算,最终得到小分子化合物结合活性的排名[5-7]。而基于配体的虚拟筛选方法不需要知道目标蛋白质受体的结构,代表性的方法包括药效团模型、定量构效关系和结构相似性等方法[8-9]。相对于基于配体的虚拟筛选,基于结构的虚拟筛选能避免活性化合物结构微小变化引起的活性改变[10],对小分子配体的活性值预测更加准确。
常用的分子对接软件包括AutoDock4[11]、AutoDock Vina[12]、AutoDock Vina 1.2.0 [13]和Smina等[14]可以进行基于结构的虚拟筛选,其中,AutoDock Vina提高了结合模式预测的平均准确度,通过使用更简单的打分函数加快了搜索速度,是应用最广泛的分子对接软件。这些分子对接软件分别采用不同的搜索算法和打分函数进行分子结合活性预测,需要耗费大量时间和计算资源来完成分子对接计算,然而在实际虚拟筛选时,筛选的候选化合物越多,可以更大可能的搜索到合适小分子配体,提高先导化合物质量[15]。因而面对大规模分子对接时,过长的筛选时间制约了分子对接软件的应用。例如AutoDock Vina在常规计算平台上筛选10亿个化合物的数据库时,每个配体的平均对接时间为15 s,筛选所有化合物的时间大概需要476年,目前的分子对接软件无法满足现代药物研发的需求[15]。
近年来研究人员针对分子对接软件对接时间过长的缺点进行了两方面改进。一方面,提出基于AutoDock Vina改进版本的Qvina1和Qvina2分子对接软件[16-17],Qvina1提出了启发式算法减少不必要的搜索次数,改进了局部搜索算法,与AutoDock Vina相比提高了运行速度,但对接精度方面有所下降。在此基础上,Qvina2优化了启发式算法,提高了对接精度,与AutoDock Vina相比实现了20.49倍的最大加速,是已知AutoDock Vina系列中最为高效的对接软件。另一方面,虚拟筛选中的分子对接计算特别适合使用并行计算加速,GPU(Graphic processing unit)因其强大的并行处理硬件架构特别适合应用于分子对接软件[18-19]。GPU具有数千个计算核心,可提供强大的计算性能,性价比较高且易于开发,并且有完善的开发标准,例如并行计算架构(CUDA)和开放运算语言(OpenCL)[20]。近年来,考虑到分子对接软件的特点,基于GPU的异构体系也被应用于改进分子对接软件[21],例如实现了AutoDock4的加速版本AutoDock4-GPU[22],在细粒度上并行了拉马克遗传算法,取得了很好的加速比。但AutoDock4的搜索效率很低[13],制约了AutoDock4-GPU的加速性能。
本文提出一种基于GPU的QVina 2并行化方法Qvina2-GPU,在目前AutoDock Vina系列中最为高效的Qvina2基础上,利用GPU硬件高度并行体系加速分子对接过程。具体包括增加初始化分子构象数量,大量线程分别对应不同的初始构象,使得每个线程独立承担蒙特卡罗搜索算法子任务,独立搜索最佳的分子构象,即通过增加蒙特卡罗的迭代搜索的广度以减少每次蒙特卡罗迭代搜索深度,并利用Wolfe-Powell准则改进局部搜索算法,相对于QVina 2中基于Armijo准则搜索算法,提高了对接精度,进一步减少蒙特卡罗迭代搜索深度,从而显著减少了蒙特卡罗构象搜索时间,减少了分子对接软件的整体运行时间。本文的贡献归纳如下:
1) 提出基于GPU的QVina 2并行化方法Qvina2-GPU,设计QVina2-GPU异构并行架构,增加初始化分子构象数量,扩展蒙特卡罗的迭代局部搜索中线程的并行规模,每个线程独立承担蒙特卡罗搜索算法子任务,通过增加蒙特卡罗迭代搜索广度以减少每次蒙特卡罗迭代搜索深度。
2) 提出基于Wolfe-Powell准则的局部搜索算法,通过迭代步长的优化,改进了QVina 2中基于Armijo准则搜索算法,提高了分子对接精度,进一步减少蒙特卡罗迭代搜索深度。
3) 使用公开数据库中140个小分子复合物[22]作为测试数据集,实验结果验证了在保证对接精度的条件下,我们提出的QVina2-GPU对Qvina2的平均加速比达到5.18倍,最大加速比达到12.28倍,具有很大的实际应用前景。
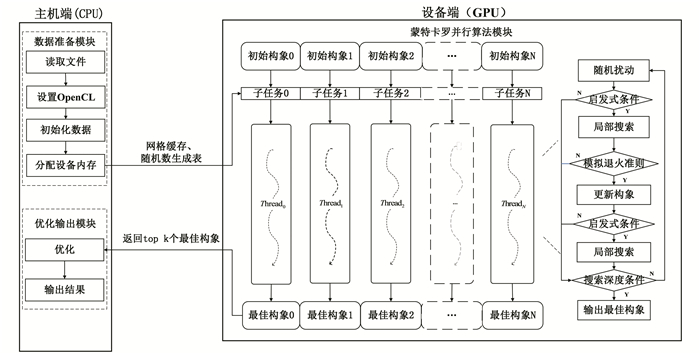
1 QVina-GPU异构并行架构QVina2-GPU异构并行架构如图 1所示,从图中可以看出,QVina2-GPU整体架构由主机端和设备端组成,主机端由数据准备模块和优化输出模块组成,这部分软件运行在CPU平台上,主要完成环境配置、数据输入以及筛选最优分子构象的功能;设备端运行蒙特卡罗并行算法模块,利用GPU并行化处理能力进行算法加速,主要思想是通过大量增加蒙特卡罗迭代搜索的初始态数量,以减少每次搜索深度,这样在保证全局优化搜索结果一致的情况下,大量减少了分子对接软件运行时间。
|
图 1 QVina2-GPU的异构并行架构 Figure 1 Heterogeneous parallel architecture of QVina2-GPU |
数据准备模块包括读取文件、配置环境、初始化数据和分配设备内存四个操作,为设备端基于GPU的蒙特卡罗并行算法的输入做准备。
1) 读取文件模块用于读取配体和受体的格式文件和配置文件。格式文件存储受体和配体原子坐标、部分电荷和原子种类信息;配置文件主要包含对接中心、对接盒子的体积、线程数和搜索深度,其中线程数N是设备端子任务的数量,搜索深度D决定蒙特卡罗并行算法迭代次数的大小。
2) 设置Opencl模块用于配置QVina2-GPU的异构并行环境,配置环境主要包括识别并选择平台和设备,创建OpenCL上下文、命令队列、程序对象和内核等OpenCL环境。
3) 初始化数据包括生成网格缓存和随机数生成表,分别用于计算分子构象能量以及生成初始化分子构象,作为蒙特卡罗迭代搜索的初始态输入。
4) 分配设备内存模块根据设定的子任务数量N,将生成的网格缓存、随机数生成表、初始化分子构象分配在只读内存的设备存储器中,便于设备端读取数据。
优化输出模块对设备端基于GPU的蒙特卡罗并行算法的输出数据进行处理。设备端每个线程运行蒙特卡罗并行算法得到的最优分子构象分配在全局存储器中,从N个分子构象中选取前k个最佳分子构象返回给主机端的优化输出模块,该模块对k个最佳构象进行精细的局部搜索,并根据搜索结果输出包含全局最优分子构象的配体文件。
2 基于GPU的蒙特卡罗并行算法从图 1可以看出设备端的基于GPU的蒙特卡罗并行算法主要两个部分:1)分配N个蒙特卡罗迭代搜索初始态;2)GPU子任务执行的基于Wolfe-Powell准则的蒙特卡罗搜索算法。
2.1 初始化蒙特卡罗迭代搜索分子构象是指配体小分子和靶标蛋白质结合时配体的位置和姿态,蒙特卡罗搜索算法目的是在分子构象空间中找到一个最佳配体分子构象,并在此基础上通过打分函数来计算配体和靶标结合的能量值,分子构象Ci∈iNC由一系列变量构成,具体表示为
| $ C_i=\left[\left(x^i, y^i, z^i\right), \left(a^i, b^i, c^i, d^i\right), \left(\varphi_1^i, \varphi_2^i, \cdots, \varphi_{N_{ {rot }}}^i\right)\right]^{\mathrm{T}} $ | (1) |
其中,(xi, yi, zi)表示分子构象Ci在搜索空间中的位置,(ai, bi, ci, di)表示刚体方向四元数,(φ1i, φ2i, …, φNroti)表示分子构象中可旋转键的扭转角度,Nrot表示可旋转键的个数, NC是分子构象的维度数。
基于GPU的蒙特卡罗并行算法构造出N个初始化分子构象£={C1, …, CN},并利用GPU并行化处理能力,创建N个线程数,使得分子构象Ci∈£作为线程Ti的输入值,运行GPU子任务执行的蒙特卡罗算法,搜索出针对该初始分子构象Ci的最佳构象Ci*。从上述描述可以看出,大量线程分别对应不同的初始构象,使得每个线程独立承担蒙特卡罗搜索算法子任务,独立搜索最佳的分子构象。因而,大量的搜索线程可以实现对分子构象空间的有效搜索,可以减少单独线程蒙特卡罗搜索算法的搜索深度,在保证全局优化搜索结果一致的情况下,显著减少了分子对接软件运行时间。
2.2 子任务执行的基于Wolfe-Powell准则的蒙特卡罗搜索每个线程运行的基于Wolfe-Powell准则蒙特卡罗搜索算法表示为GPU子任务,蒙特卡罗的算法流程如图 2所示,大体可以分为5步,包括随机扰动、启发式条件、局部搜索和模拟退火准则四个模块。下面以线程Ti处理初始分子构象Ci∈£为例说明子任务执行基于Wolfe-Powell准则的模特卡罗搜索过程。

|
图 2 基于Wolfe-Powell准则的蒙特卡罗搜索算法流程 Figure 2 Flow of Monte Carlo search algorithm based on Wolfe Powell criterion |
Step 1 首先对用随机抖动函数R(·)对初始化分子构象Ci进行处理:
| $ \hat{C}_i=R\left(C_i\right) $ | (2) |
其中,
| $ \mathrm{E}_{\hat{C}_i}=f\left(\hat{C}_i\right) $ | (3) |
其中,能量计算函数f(·)根据构象
Step 2 对于随机抖动构象
| $ \operatorname{sign}\left(\left.\frac{\partial f(C)}{\partial c_i}\right|_{C=\hat{c}_i}\right) \cdot \operatorname{sign}\left(\left.\frac{\partial f(C)}{\partial c_i}\right|_{C=\hat{c}_i}\right) \leqslant 0 $ | (4a) |
| $ \begin{gathered} \operatorname{sign}\left(\left.\frac{\partial f(C)}{\partial c_i}\right|_{C=\hat{C}_i}\right) \cdot \operatorname{sign}\left([ f ( \hat { C } _ { i } ) - f ( \overline { C } _ { i } ) ] \left[\left(\hat{C}_i\right)_i-\right.\right. \\ \left.\left.\left(\bar{C}_i\right)_i\right]\right) \leqslant 0 \end{gathered} $ | (4b) |
其中,ci∈C表示构象Ci中的第i个变量,
Step 3 对满足启发式条件的构象
1) 计算搜索方向pk:Bkpk=-▽f(xk),其中,f(·)为能量计算函数,xk和Bk分别是第k步搜索构象和海森矩阵。
2) 确定基于Wolfe-Powell准则的步长αk:
| $ \alpha_k=\arg \min\limits _{\alpha \in i} f\left({\bf{x}}_k+\alpha {\bf{p}}_k\right) $ | (5) |
上式表达的是精确线性搜索中可接受的搜索步长αk,实际执行中,我们采用非精确线性搜索中满足Wolfe-Powell准则的搜索步长αk,Wolfe-Powell准则描述具体见2.3节。
3) 更新搜索构象xk+1:xk+1=xk+αkpk, 其中,pk和αk分别是上面计算的搜索方向和步长。
4) 更新海森矩阵Bk+1:
| $ {\bf{B}}_{k+1}={\bf{B}}_k+\frac{y_k y_k^{\mathrm{T}}}{y_k^{\mathrm{T}} s_k}-\frac{{\bf{B}}_k s_k s_k^{\mathrm{T}} {\bf{B}}_k^{\mathrm{T}}}{s_k^{\mathrm{T}} {\bf{B}}_k s_k} $ | (6) |
其中,sk=αkpk, yk=▽f(xk+1)-▽f(xk), 海森矩阵更新需要耗费计算资源,减少BFGS迭代搜索的深度可以有效的减少海森矩阵的更新,有效提高计算效率。如果‖▽f(xk+1)‖≤ε或迭代次数k=T,ε为预定值,则BFGS迭代结束,并设局部搜索的新构象Ci=xk+1。
Step 4 对于局部搜索得到的新构象Ci,比较新构象Ci的能量和扰动前的构象Ci的能量,利用模拟退火准则以概率判断是否接受新构象Ci,如果Ci被接受继续执行,如果不被接受就返回Step1,这样可以在一定概率上使得搜索空间跳出局部极小值,收敛到全局最小值,模拟退火准则的接受概率P为
| $ P= \begin{cases}1, \;\;\;\;\;\;\;\;\;\;\;\;\;\; \mathrm{E}_{C_i}>\mathrm{E}_{\bar{C}_i}, \\ \frac{\operatorname{Exp}\left(\mathrm{E}_{C_i}-\mathrm{E}_{\bar{C}_i}\right)}{1.2}, E_{\mathrm{C}_{\mathrm{i}}} \leqslant E_{\bar{C}_{\mathrm{i}}}, \end{cases} $ | (7) |
其中,ΕCi表示新构象Ci的能量,ΕCi表示扰动前的构象Ci的能量,如果ΕCi < ΕCi则接受新构象Ci,如果ΕCi≥ΕCi,以exp(ΕCi-ΕCi)/1.2的概率接受新构象Ci, 通过接受更差的构象可以更广泛地搜索全局最优构象,避免陷入局部最优解。
Step 5 对构象Ci再进行一次启发式条件判断和局部搜索,选取能量记录更优构象Ci*,如果迭代次数未达到搜索深度D,返回Step 1对分子构象继续随机扰动,如果迭代次数达到D,则输出该线程中的最佳分子构象Ci*。
2.3 基于Wolfe-Powell准则的局部搜索算法蒙特卡罗搜索算法中的局部搜索算法是找到最佳配体分子构象的重要模块,相对于其他模块耗费时间较长。QVina2利用基于不精确线性搜索Armijo准则局部搜索对分子构象进行优化,Armijo准则的主要思想是确定搜索方向pk, 找到合适的步长αk,保证目标函数值下降,且下降量满足不等式关系:
| $ f\left(\boldsymbol{x}_k+\alpha_k {\bf{p}}_k\right) \leqslant f\left(\boldsymbol{x}_k\right)+c_1 \alpha_k {\bf{p}}_k^{\mathrm{T}} \nabla f\left(\boldsymbol{x}_k\right) $ | (8) |
其中,c1为常数且满足c1∈(0, 1)。在步长更新的过程中,公式(8)主要目的是限制步长,确保下一个搜索构象的能量有足够的下降,但是该条件不能确保步长值接近最佳步长,因为只要步长足够小就可以满足公式(8),如果步长过小会增加BFGS搜索迭代的次数。为了克服Armijo准则这一缺陷,我们提出使用基于Wolfe-Powell准则的局部搜索算法。Wolfe-Powell属于不精确线性搜索准则,相比于Armijo准则,Wolfe-Powell准则更适合BFGS算法,可以保证海森矩阵迭代的正定性,增加了对步长的限制条件:
| $ -{\bf{p}}_k^{\mathrm{T}} \nabla f\left(\boldsymbol{x}_k+\alpha_k {\bf{p}}_k\right) \leqslant-c_2 {\bf{p}}_k^{\mathrm{T}} \nabla f\left(\boldsymbol{x}_k\right) $ | (9) |
其中,c2为常数且满足c2∈(0, 1)。公式(9)的作用是限制过小的步长,保证能量函数的方向导数充分下降,找到更合适的步长,从而以更小的迭代次数找到更佳的分子构象,提高对接精度。因而,QVina2-GPU通过基于Wolfe-Powell准则局部搜索可以进一步减少蒙特卡罗迭代算法的搜索深度,在保证全局优化搜索结果一致的情况下,提高软件对接速度。Wolfe-Powell准则确定步长的迭代过程如下:
Step 1 给定c1∈(0, 0.5),c2∈(c1, 1),令α0=1,n=0,设定步长迭代次数L。
Step 2 f(xk+1)=f(xk+αnpk), 其中pk和xk分别是已知的搜索方向和搜索构象,αn为第n次迭代的步长。
Step 3 若αn满足公式(8)和(9)或步长迭代次数n=L,则αk=αn并退出步长更新迭代。若αn不满足公式(8),令b=αn,αn=αn/2,n=n+1,返回Step 3。
Step 4 若αn不满足公式(9),令αn=min(2αn, 0.5*(αn+b)),n=n+1,返回Step 3。
综上所述,基于Wolfe-Powell准则的蒙特卡罗搜索算法如下面所述,算法流程大体可以分为5步,包括随机扰动、启发式条件、局部搜索和模拟退火准则四个模块。基于Wolfe-Powell准则的蒙特卡罗搜索算法交给GPU的子任务执行,这样大量的子任务可以并行执行搜索算法,数量众多的搜索线程可以实现对分子构象空间的有效搜索,可以减少单独线程蒙特卡罗搜索算法的搜索深度,在保证全局优化搜索结果一致的情况下,显著减少了分子对接软件运行时间。
3 实验及性能分析 3.1 实验环境及数据集QVina2-GPU的异构并行架构通过开放运算语言OpenCL实现,实验环境的CPU为4核的Intel(R) Xeon(R) Gold 6130 CPU @2.10GHz,GPU为NVIDIA GeForce RTX 3090,操作系统为Windows 10,编译器为Visual Studio 2019,CUDA的版本为11.1,OpenCL的版本为3.0。
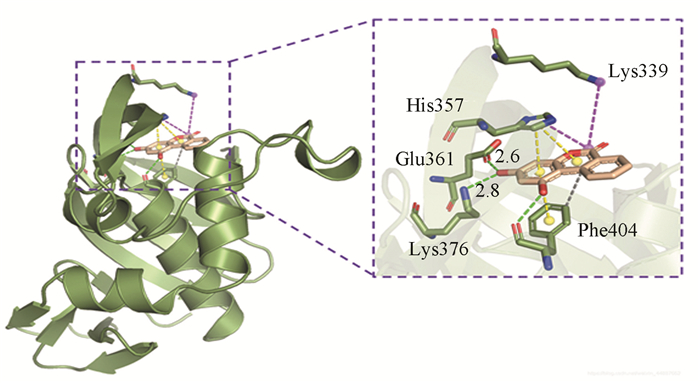
图 3显示了配体MGT1484和药物靶标受体PROTEIN分子对接结果的3D结构示意图,图中左侧框图为分子对接过程的对接口袋,右侧框图为具体的对接过程,受体和配体之间的虚线为分子作用力。分子对接软件就是通过打分函数计算分子对接过程的结合能量,来预测药物靶标受体和配体结合的可能性,选出具有可能成药的活性化合物。
|
图 3 药物靶标受体和配体分子对接示意图 Figure 3 Schematic diagram of drug target receptor and ligand molecular docking |
算法:基于Wolfe-Powell准则的蒙特卡罗搜索算法
输入:
①N个随机初始构象{C1, …, CN}:
②搜索深度:D;
③set d=0;
④Parallel for Ci(i=0, ..., N) do
⑤while d < D do
⑥根据公式(2)随机扰动Ci得到候选构象Ci;
⑦If
⑧根据基于Wolfe-Powell准则的BFGS搜索算法得到新构象Ci,
⑨根据公式(7)计算模拟退火算法接受概率P,
⑩If以P概率接受Ci & Ci满足启发式条件
⑪根据基于Wolfe-Powell准则的BFGS搜索算法得到新构象Ci*
⑫end if
⑬end if
⑭d=d+1;
⑮end while
输出:排名前k个最佳分子构象{C0*, C1*, …, Ck-1*}
使用包含140个药物靶标受体-配体复合物的数据集作为实验数据集,其中85个来自Astex多样性集[23]、35个来自CASF-2013[24]和20个来自蛋白质数据库[25],该数据集包含了广泛的配体复杂度和靶标性质。数据集根据原子数目Natom分为简单复合物、中等复杂复合物和复杂复合物,其中,简单复合物的数量为46,原子数目Natom范围为[5, 23],中等复杂复合物的数量为51,Natom范围为[24, 36],复杂复合物的数量为43,Natom范围为[37, 108],三种复合物对应配体复杂度越来越高。
3.2 实验指标和对比算法对接精度和对接时间是评估分子对接软件性能最重要的两个指标,对接精度主要由对接分数Score和和RMSD(Root mean square deviation)决定,1)对接分数Score表示配体和受体之间的结合能,Score越低则结合越稳定,2)RMSD表示分子对接软件搜索得到的构象与生物实验获得的X-ray结构(标准)之间的相似性,RMSD越低则表示搜索到的构象精度越高,当RMSD小于2Å(10-10m)时,该构象是可以被接受,表示成功预测。3)对接时间是整个分子对接软件的运行时间,对接时间越短,对接精度越高,表示分子对接软件性能越好。
在相同的实验环境中比较QVina2与QVina2-GPU分子对接软件的性能,两种算法的介绍如下:
1) QVina2(Quick Vina2):是一种快速准确的分子对接软件,并提出了启发式算法改进了局部搜索算法,与传统的分子对接软件相比提高了运行速度。
2) QVina2-GPU:是我们在QVina2对接软件基础上,提出的一种异构并行架构并实现了基于Wolfe-Powell准则的蒙特卡罗搜索,利用GPU硬件高度并行体系加速分子对接过程。
在分子对接软件运行前,需要先设置配置文件。QVina2的配置文件中的配置参数包括搜索空间的中心、对接盒子的体积,另外还包括两个重要的参数:初始化分子构象数量N和搜索深度D,二者反应的分子构象搜索的广度和深度,其中分子对接软件的运行时间主要由搜索深度D决定,
3) QVina2默认参数N为8,搜索深度D随着配体分子的复杂度增加而增大,对于简单分子复合物、中等复杂复合物和复杂复合物的平均搜索深度分别为16 170、29 663和41 212。
QVina2-GPU利用GPU并行化处理能力大量增加初始化分子构象数量N,使得大量线程分别对应不同的分子初始构象,使得每个线程独立承担蒙特卡罗搜索算法子任务,独立搜索最佳的分子构象。以减少每个子任务的每次搜索深度D,在保证全局优化搜索结果一致的情况下,显著减少了分子对接软件运行时间。下面将重点讨论初始化分子构象数量N和搜索深度D对性能的影响。
3.3 两种准则对接精度比较比较对象QVina2使用的是基于Armijo准则的蒙特卡罗搜索算法,我们提出的QVina2-GPU使用的是基于Wolfe-Powell准则的蒙特卡罗搜索算法。因而,本次实验讨论基于Wolfe-Powell准则的蒙特卡罗搜索算法和基于Armijo准则的蒙特卡罗搜索算法的对接精度,即对接分数Score和和RMSD指标。
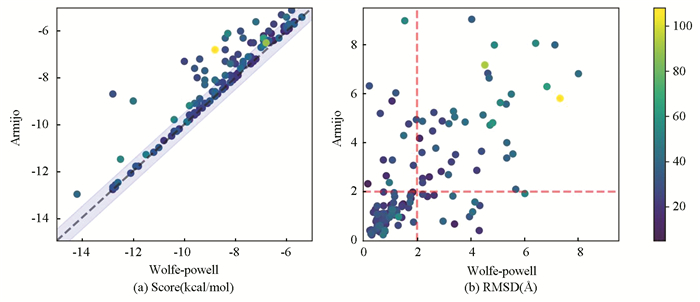
在140个配体小分子复合物上进行对接实验,对比两种准则下对对接分数Score和RMSD的影响,实验结果如图 4所示,其中图 4a表示140个配体小分子在两种准则条件下的Score,其中Score的单位是kcal/mol,表示每摩尔分子千卡能量,图 4b表示两种准则条件下的RMSD指标。两幅图的纵坐标表示基于Armijo准则的指标,横坐标表示基于Wolfe-Powell准则的指标。颜色条表示配体中的原子数,颜色条从深到浅对应原子数目由少至多,即配体分子复杂度越来越高。
|
图 4 两种准则的Score和RMSD对比图(Score和RMSD越小越好) Figure 4 Comparison diagram of score and RMSD of the two criteria (the smaller the score and RMSD, the better) |
结果显示数据集中60.71%的复合物位于图 4a的对角线上方,表明使用Wolfe-Powell准则得到的对接分数Score小于Armijo准则的Score,即Wolfe-Powell准则性能优于Armijo准则;有39.29%的复合物位于图 4a的对角线上,表明用Wolfe-Powell准则得到的Score与Armijo准则相同;基于Wolfe-Powell准则的蒙特卡罗搜索算法有63.57%构象位于图 4b中垂直红色虚线左边区域内,表示RMSD指标小于2Å(10-10m)可被接受,而基于Armijo准则蒙特卡罗搜索算法只有59.28% 构象位于图 4b水平红色虚线下方区域内,可被接受。结果表明,相对于QVina2中基于Armijo准则蒙特卡罗搜索算法,我们提出的基于Wolfe-Powell准则的蒙特卡罗搜索算法具有更高的对接精度,在Score和RMSD指标中均明显优于基于Armijo准则蒙特卡罗搜索算法。
3.4 QVina2-GPU中初始化分子构象数和搜索深度对性能的影响不失一般性,从实验数据集中随机选取8个复合物,QVina2的初始化分子构象数N和搜索深度D按照配置文件设置并固定不变,QVina2-GPU的搜索深度D设置为1,初始化分子构象数N从100增大到8 000,讨论N变化对QVina2-GPU的对接分数Score、RMSD和对接时间的影响。
如表 1-表 3所示,复合物从上到下对应配体复杂度越来越高,表 1-表 2可以看出初始化分子构象数N为800可以保证QVina2-GPU的Score和RMSD指标与QVina2相当,继续增加初始化分子构象数N,QVina2-GPU的Score和RMSD指标将优于QVina2。表 3的实验结果表明在所有情况下QVina2-GPU对接时间相对于QVina2有了较大的降低,而且QVina2-GPU对接时间随着初始化分子构象数N的增加而增加,对于复杂复合物这种增加的趋势更加明显,因此,可以得出:增加初始化分子构象数N,可以有效的提高分子对接精度,但同时也增加了对接时间开销。综上所述,为了在保证精度前提下尽量减少分子对接时间,下面的实验中,将QVina2-GPU的初始化分子构象数N设置为800。
| 表 1 初始化分子构象数N对Score的影响(Score越小越好,标粗表示性能达到或优于QVina2) Table 1 Effect of initial molecular conformation number N on score (The smaller the score, the better. The bold numbers mean that the performance reaches or exceeds QVina2) |
| 表 2 初始化分子构象数N对于RMSD的影响(RMSD越小越好,标粗表示性能达到或优于QVina2) Table 2 Effect of initial molecular conformation number N on RMSD (The smaller the RMSD, the better. The bold numbers indicate that the performance reaches or exceeds QVina2) |
| 表 3 初始化分子构象数N对于对接时间的影响(对接时间越小越好,标粗表示性能达到或优于QVina2) Table 3 Effect of initial molecular conformation number N on docking time (The smaller the docking time, the better. The bold numbers indicate that the performance reaches or exceeds QVina2) |
在确定初始化分子构象数N后,我们将搜索深度D从1增大到30,探究D对于QVina2-GPU的对接精度和对接时间的影响,表 4-表 6可以看出对于简单复合物如5tim等,增大搜索深度D对Score、RMSE和对接时间的影响很小;对于中等复杂复合物如1hvy等,随着搜索深度D增加,对接精度指标Score和RMSE总体上有所减少,但对接时间缓慢增加;对于复杂复合物3er5等,增大搜索深度D,对接精度指标Score和RMSE同样总体上有所减少,但对接时间增加很快,会导致很大的时间开销。
| 表 4 搜索深度D对Score的影响(Score越小越好,标粗表示性能达到或优于QVina2) Table 4 Effect of search depth D on score (The smaller the score, the better. The bold numbers indicate that the performance reaches or exceeds QVina2) |
| 表 5 搜索深度D对RMSD的影响(RMSD越小越好,标粗表示性能达到或优于QVina2) Table 5 Effect of search depth D on RMSD (The smaller the RMSD, the better. The bold numbers indicate that the performance reaches or exceeds QVina2) |
| 表 6 搜索深度D对于对接时间的影响(对接时间越小越好,标粗表示性能达到或优于QVina2) Table 6 Effect of Search Depth D on docking time (The smaller the docking time, the better. The bold numbers indicate that the performance reaches or exceeds QVina2) |
综上所述,为了在保证精度前提下尽量减少分子对接时间,特别是考虑到搜索深度D对于复杂复合物对接时间的影响特别明显。因此,接下来的实验,我们将数据集140个复合物的初始化分子构象数N设为800,搜索深度D设为1,以最少的对接时间保证了分子对接精度。
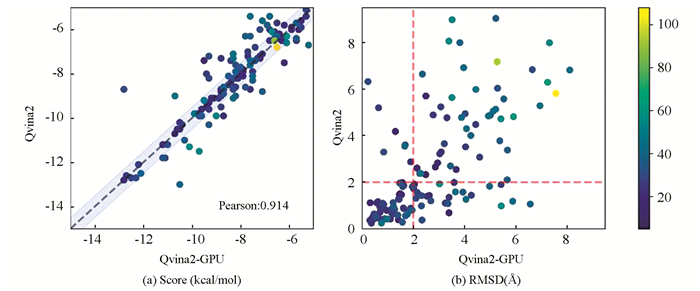
3.5 QVina2-GPU与QVina2的性能对比首先对比了QVina2-GPU和QVina2在140个复合物上的对接分数Score和RMSD对接精度指标,两幅图的纵坐标表示QVina2的性能指标,横坐标表示QVina2-GPU的性能指标。颜色条表示配体中的原子数,颜色条从深到浅对应原子数目由少至多,即配体分子复杂度越来越高。
对接分数Score结果如图 5a所示,大多数复合物分布在对角线周围,其对接分数的皮尔森相关系数为0.914,表示它们之间存在极强相关性,即QVina2-GPU和QVina2对接分子Score的指标基本相同;图 5b显示大多数复合物落入左下角区域,QVina2(水平红色虚线下方区域内)和QVina2-GPU(垂直红色虚线下方区域内)分别有58.28%和55%的复合物的预测结果可被接受,结果表明本文提出的QVina2-GPU在初始化分子构象数N为800和搜索深度D为1的条件下,达到了QVina2的对接精度。
|
图 5 QVina2-GPU与QVina2的Score和RMSD对接精度对比图(N=800,D=1) Figure 5 Comparison chart of score and RMSD docking accuracy between QVina2-GPU and QVina2(N=800, D=1) |
下面重点讨论一下QVina2-GPU和QVina2在140个复合物上的对接时间指标,这里我们使用两个对接时间指标,对接时间加速比Acc和蒙特卡罗时间加速比Accd,定义如下:
| $ A c c=\frac{T_{\text {qvina } 2}}{T_{\text {qvina2-gpu }}}, A c c_d=\frac{T_{\mathrm{mc}}}{T_{\mathrm{mc}-\mathrm{gpu}}} $ | (10) |
式中,Tqvina2是QVina2分子对接计算的对接时间,Tqvina2-gpu是QVina2-GPU分子对接计算的对接时间。QVina2与QVina2-GPU软件运行中,蒙特卡罗迭代搜索算法都是最耗时的部分,因而,Tmc为QVina2中基于CPU的蒙特卡罗算法的运行时间,Tmc-gpu为QVina2-GPU的蒙特卡罗运行时间。对接时间加速比Acc和蒙特卡罗时间加速比Accd数值越大,说明我们提出的QVina2-GPU相对于QVina2有较高的加速比,即运行时间相对于QVina2有显著的减少。
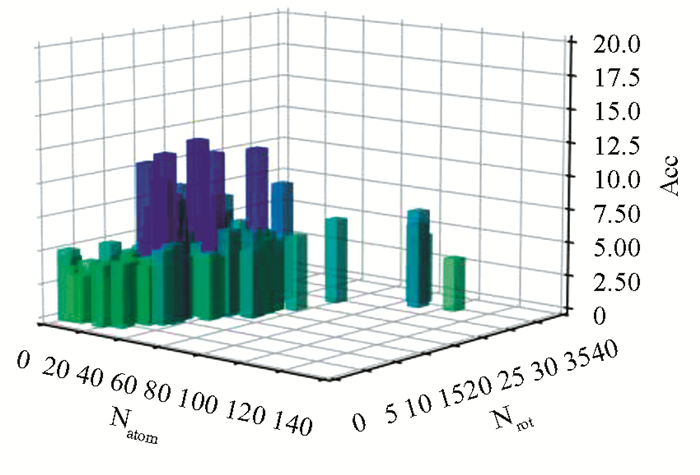
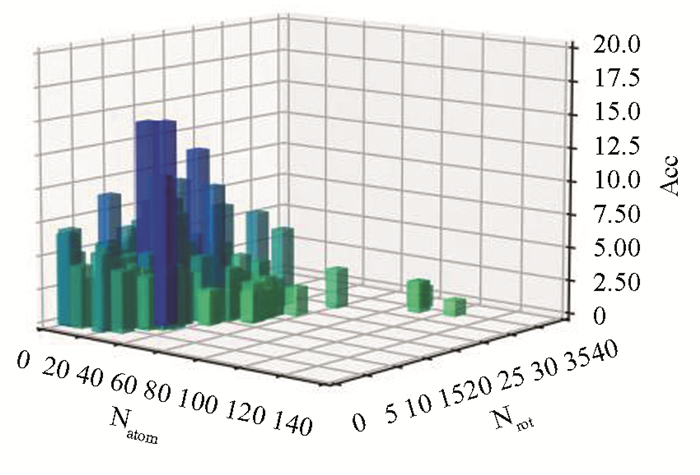
图 6和图 7给出了140个复合物的对接时间加速比Acc和蒙特卡罗时间加速比Accd。为了区分不同复杂度配体分子的加速比情况,三维坐标的横纵坐标分别表示配体的原子数目Natom和可旋转键数目Natom,配体的复杂度由原子数目Natom和可旋转键数目Natom决定,一般来说Natom和Natom越大,配体的复杂度越高。图 6和图 7中每个条形柱体分别表示配体的复杂程度和对应的对接时间加速比Acc和蒙特卡罗时间加速比Accd,对接时间加速比的蓝色柱状条表示加速比达到10的复合物,蒙特卡罗时间加速比的蓝色柱状条为加速比达到60的复合物,越靠近蓝色加速比越高,图 5可以看出Acc分布范围在3.11倍~12.28倍之间,图 7可以看出Accd分布范围为6.48倍~60.28倍,其中,2bm2复合物加速效果最好,它的蒙特卡罗时间加速比Acc达到了60.28倍,对接时间加速比Accd达到了12.28倍。上面数据充分说明了我们提出的QVina2-GPU在不同类型的复合物上都有明显的加速效果,显著的减少了分子对接的计算时间,这对于需要大量筛选配体分子的生物实验特别有意义。为进一步显示QVina2-GPU加速比性能,三种配体分子复杂度下的平均加速比结果(见表 7),结果表明,最大平均蒙特卡罗时间加速比为22.91倍,最大平均对接时间加速比为5.71倍,三种不同复杂度复合物条件下,QVina2-GPU都取得了令人满意的加速比,总体平均蒙特卡罗时间加速比和平均对接时间加速比分别到达了18.63和5.18。从上面的分析可知,QVina2-GPU利用GPU并行化处理能力大量增加初始化分子构象数量N,使得大量线程分别对应不同的分子初始构象,使得每个线程独立承担蒙特卡罗搜索算法子任务,增加初始化分子构象数量N以减少每个子任务的每次搜索深度D,从而显著减少了蒙特卡罗构象搜索时间,减少了分子对接软件的整体运行时间。平均对接时间加速比随着复杂度的增大而提高,这是由于随着复杂度的增加,蒙特卡罗搜索算法运行时间在整个软件运行时间比例加重,平均对接时间加速比随着增加。
|
图 6 140个复合物的对接时间加速比 Figure 6 Docking time acceleration ratio of 140 composites |
|
图 7 140个复合的物蒙特卡罗时间加速比 Figure 7 Monte Carlo time acceleration ratio of 140 compounds |
| 表 7 三种配体复杂度的平均时间和平均时间加速比 Table 7 Average time and average time acceleration ratio of three ligand complexities |
为了区分Vina-GPU[26]和QVina2-GPU两种方法在性能上的不同,我们从Vina-GPU论文里获取可执行程序,在相同的硬件平台实验环境下,对上文提到的随机8个复合物对比QVina2-GPU与Vina-GPU的对接分数Score和RMSD对接精度指标和对接时间,如表 8所示,实验表明,对于简单分子和中等复杂分子QVina2-GPU可以在对接精度基本相同的情况下加速Vina-GPU,对于复杂分子,我们提出的QVina2-GPU在对接精度略微下降的条件下,运行时间上有明显的减少,相对于Vina-GPU的加速比最大可达32.92,这对于实际药物筛选应用具有很大的意义。
| 表 8 Vina-GPU与QVina2-GPU的性能对比 Table 8 Performance comparison between Vina GPU and QVina2 GPU |
本文提出基于GPU加速的分子对接软件并行化方法QVina2-GPU,针对Qvina2在大型虚拟数据库中筛选时间过长的情况,通过增加初始化分子构象数量来扩展蒙特卡罗的迭代局部搜索中线程的并行规模,减少蒙特卡罗迭代搜索算法的搜索步数,而且利用Wolfe-Powell准则改进局部搜索算法,提高了对接精度,进一步减少蒙特卡罗迭代算法的搜索深度,提高分子对接软件的运行速度。在公开的药物靶标受体-配体复合物的数据集上验证了不同类型复合物上的平均模特卡罗时间加速比和平均对接时间加速比,结果表明QVina2-GPU在达到Qvina2分子对接精度的条件下,相对于QVina2有显著的加速效果。QVina2-GPU的代码可以在https://github.com/DeltaGroupNJUPT/QuickVina2-GPU上获得,其中包含可执行程序和程序使用说明,便于科研人员使用。
由于QVina2-GPU计算构象的能量使用的依旧是QVina2的能量计算函数,是一种经验公式,筛选出能量较低的复合物用于生物实验中,存在较高的偏差[27],近年来已有学者研究基于深度学习的能量计算函数。未来,我们的工作将通过研究新的能量计算函数来提高QVina2-GPU的对接性能。
| [1] |
KONTOYIANNI M. Docking and virtual screening in drug discovery[J]. Methods in Molecular Biology, 2017, 1647: 255-266. DOI:10.1007/978-1-4939-7201-2_18 (  0) 0) |
| [2] |
WALTERS W P, STAHL M T, MURCKO M A. Virtual screening-an overview[J]. Drug Discovery Today, 1998, 3(4): 160-178. DOI:10.1016/S1359-6446(97)01163-X (  0) 0) |
| [3] |
MURCKO M, CARON P. Transforming the genome to drug discovery[J]. Drug Discovery Today, 2002, 7(11): 583-584. DOI:10.1016/S1359-6446(02)02267-5 (  0) 0) |
| [4] |
LAVECCHIA A, GIOVANNI C. Virtual screening strategies in drug discovery: a critical review[J]. Current Medicinal Chemistry, 2013, 20(23): 2839-2360. DOI:10.2174/09298673113209990001 (  0) 0) |
| [5] |
KOOISTRA A J, VISCHER H F, MCNAUGHT-FLORES D, et al. Function-specific virtual screening for GPCR ligands using a combined scoring method[J]. Scientific Reports, 2016, 6: 28288. DOI:10.1038/srep28288 (  0) 0) |
| [6] |
BALLESTER P J. Selecting machine-learning scoring functions for structure-based virtual screening[J]. Drug Discovery Today: Technologies, 2019, 32-33: 81-87. DOI:10.1016/j.ddtec.2020.09.001 (  0) 0) |
| [7] |
LI Hongjian, SZE K H, LU Gang, et al. Machine-learning scoring functions for structure-based virtual screening[J]. Wiley Interdisciplinary Reviews-Computational Molecular Science, 2021, 11(1): e1478. DOI:10.1002/wcms.1428 (  0) 0) |
| [8] |
GEPPERT H, VOGT M, BAJORATH J. Current trends in ligand-based virtual screening: molecular representations, data mining methods, new application areas, and performance evaluation[J]. Journal of Chemical Information and Modeling, 2010, 50(2): 205-216. DOI:10.1021/ci900419k (  0) 0) |
| [9] |
SANTANA K, DO NASCIMENTO L D, LIMA E, LIMA A, et al. Applications of virtual screening in bioprospecting: facts, shifts, and perspectives to explore the chemo-structural diversity of natural products[J]. Frontiers in Chemistry, 2021, 9: 662688. DOI:10.3389/fchem.2021.662688 (  0) 0) |
| [10] |
KUBINYI H. Similarity and dissimilarity: A medicinal chemist's view[J]. Perspect in Drug Discovery and Design, 1998(9/10/11): 225-252. DOI:10.1023/A:1027221424359 (  0) 0) |
| [11] |
MORRIS G M, HUEY R, LINDSTROM W, et al. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility[J]. Journal of Computational Chemistry, 2009, 30(16): 2785-2791. DOI:10.1002/jcc.21256 (  0) 0) |
| [12] |
TROTT O, OLSON A J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading[J]. Journal of Computational Chemistry, 2009, 31(2): 455-461. DOI:10.1002/jcc.21334 (  0) 0) |
| [13] |
EBERHARDT J, SANTOS-MARTINS D, TILLACK A, et al. AutoDock Vina 1.2.0: New docking methods, expanded force field, and python bindings[J]. Journal of Chemical Information And Modeling, 2021, 61(8): 3891-3898. DOI:10.26434/chemrxiv.14774223 (  0) 0) |
| [14] |
KOES D R, BAUMGARTNER M P, CAMACHO C J. Lessons learned in empirical scoring with smina from the CSAR 2011 benchmarking exercise[J]. Journal of Chemical Information and Modeling, 2013, 53(8): 1893-1904. DOI:10.1021/ci300604z (  0) 0) |
| [15] |
GORGULLA C, BOESZOERMENYI A, WANG Z F, et al. An open-source drug discovery platform enables ultra-large virtual screens[J]. Nature, 2020, 580(7805): 663-668. DOI:10.1038/s41586-020-2117-z (  0) 0) |
| [16] |
HANDOKO S D, OUYANG X, SU C T, et al. QuickVina: Accelerating AutoDock Vina using gradient-based heuristics for global optimization[J]. IEEE/ACM Transactions on Computational Biology & Bioinformatics, 2012, 9(5): 1266-1272. DOI:10.1109/TCBB.2012.82 (  0) 0) |
| [17] |
ALHOSSARY A, HANDOKO S D, MU Y, et al. Fast, Accurate, and reliable molecular docking with quickVina 2[J]. Bioinformatics, 2015, 31(13): 2214-2216. DOI:10.1093/bioinformatics/btv082 (  0) 0) |
| [18] |
DING Xinqiang, WU Yujin, WANG Yanming, et al. Accelerated cdocker with gpus, parallel simulated annealing, and fast fourier transforms[J]. Journal of Chemical Theory and Computation, 2020, 16(6): 3910-3919. DOI:10.1021/acs.jctc.0c00145 (  0) 0) |
| [19] |
SOLIS-VASQUEZ L, SANTOS-MARTINS D, TILLACK A F, et al. Parallelizing irregular computations for molecular docking[C]. //In 2020 IEEE/ACM 10th Workshop on Irregular Applications: Architectures and Algorithms (IA3). 2020: 12-21.
(  0) 0) |
| [20] |
FAN Mengran, WANG Jian, JIANG Huaipan, et al. Gpu-accelerated flexible molecular docking[J]. The Journal of Physical Chemistry B, 2021, 125(4): 1049-1060. DOI:10.1021/acs.jpcb.0c09051 (  0) 0) |
| [21] |
LEGRAND S, SCHEINBERG A, TILLACK A F, et al. Gpu-accelerated drug discovery with docking on the summit supercomputer: porting, optimization, and application to covid-19 research[C]. //Proceedings of the 11th ACM international conference on bioinformatics, computational biology and health informatics. 2020: 1-10. DOI: 10.1145/3388440.3412472.
(  0) 0) |
| [22] |
SANTOS-MARTINS D, SOLIS-VASQUEZ L, TILLACK A F, et al. Accelerating AutoDock4 with GPUs and gradient-based local search[J]. Journal of Chemical Theory and Computation, 2021, 17(2): 1060-1073. DOI:10.1021/acs.jctc.0c01006 (  0) 0) |
| [23] |
HARTSHORN M J, VERDONK M L, CHESSARI G, et al. Diverse, high-quality test set for the validation of proteinligand docking performance[J]. Journal of Medicinal Chemistry, 2007, 50(4): 726-741. DOI:10.1021/jm061277y (  0) 0) |
| [24] |
LI Yan, SU Minyi, LIU Zhihai, et al. Assessing protein-ligand interaction scoring functions with the CASF-2013 benchmark[J]. Nature Protocols, 2018, 13(4): 666. DOI:10.1038/nprot.2017.114 (  0) 0) |
| [25] |
BERMAN H M, BATTISTUZ T, BHAT T N, et al. The protein data bank[J]. Nucleic Acids Research, 2000, 28(1): 235-242. DOI:10.1093/nar/28.1.235 (  0) 0) |
| [26] |
TANG Shidi, CHEN Ruiqi, LIN Mengru, et al. Accelerating AutoDock Vina with GPUs[J]. Molecules, 2022, 27(9): 3041. DOI:10.3390/molecules27093041 (  0) 0) |
| [27] |
SU Minyi, YANG Qifan, DU Yu, et al. Comparative assessment of scoring functions: The CASF-2016 Update[J]. Journal of Chemical Information And Modeling, 2019, 59: 895-913. DOI:10.1021/acs.jcim.8b00545 (  0) 0) |
 2023, Vol. 21
2023, Vol. 21


