生物序列的相似性分析是生物信息学的重要研究方向之一。在早期研究中,通常采用多序列比对的方法对序列进行比较分析,许多算法现在已经非常成熟[1-3],例如使用较多的ClustalW算法。但多序列比对是基于同源序列片段间是邻接保守的假设,这与遗传重组相冲突,而且当样本量较大或序列长度较长时,比对算法的时间成本很高。因此,非比对方法[4]一经推出,立即受到研究人员的广泛关注。非比对方法不是具体比较基对,而是将序列看成是一个整体并将其转化为数值向量再进行分析比较,其优点是在计算机上计算迅速,且结果较准确。
蛋白质序列的比较分析方法大致分为两大类:图形表示方法和数值向量刻画方法。图形表示方法也称为可视化方法,其基本思想是建立一组映射,将氨基酸映射成平面或空间的点,然后将点连接起来得到空间曲线。进一步地,我们还可以从这些图形表示中提取生物序列的数值特征,利用这些数值特征进行序列分析[5-12]。数值向量刻画方法主要是将蛋白质序列转换为多维的数值向量,例如Chou K.C.[13]和Chen W.等[14]将氨基酸的20维频率向量与理化性质或者氨基酸之间的相互作用结合起来构建(20+λ)维向量来表示蛋白质序列,其中λ指的是理化性质个数或者氨基酸相互之间作用的指标数。贾美多等[15]结合氨基酸的5-字母分类模型和序列的k-字节模型,提取信息将序列转化为一个30维向量,之后利用欧氏距离求得蛋白质序列两两间的相对距离进而构建系统进化树。Xian-HuaXie等[16]使用氨基酸随机和独立放置的序列分布图之间的相对偏差来定义序列间的差异。Li Y等[17]结合氨基酸的概率、平均出现位置概率和两个相邻氨基酸的马尔科夫转移概率分布来构建蛋白质数值向量表示。Yongkun Li等[18]将蛋白质序列中20种氨基酸的数目、平均位置和位置的正则化中心二阶矩结合起来构成60维数值向量来衡量病毒之间的相似性。Lily He等[19]基于氨基酸的亲水性指数、极性需求和侧链的化学成分将氨基酸分成8类,之后融合蛋白质序列中这8类氨基酸的数量、平均位置和位置的二阶矩信息构建24维特征向量进行进化分析。朱臣臣等[20]选择3种氨基酸的理化性质绘制蛋白质序列的3D图形,再基于氨基酸的位置信息构建20个点集,分别求其转动惯量构建23维特征向量。Stephen S.-T. Yau等[21]、Qi Dai等[22]和Yufeng Liu等[23]统计序列中所有的长度为k的子串的频率,将这些数字组成向量,使用该向量刻画生物序列的特征。
蛋白质是由氨基酸组成的,已有研究表明氨基酸的物理化学性质对蛋白质序列分类和进化具有重要意义[24-25]。本文将氨基酸的10种理化性质通过主成分分析浓缩为6组主成分,对每条蛋白质序列,计算反映氨基酸理化性质的6组主成分得分均值,再融合20个氨基酸的位置信息构成一个26维的蛋白质序列特征向量,最后利用欧式距离度量蛋白质序列间的相似性并构造系统进化树。通过对三组蛋白质序列数据集的测试表明,本文的方法能将每条蛋白质序列准确聚类,结果与现有进化关系一致,说明了该方法的有效性。
1 蛋白质序列的特征向量构造 1.1 基于氨基酸理化性质的向量表示蛋白质的基本单位是氨基酸,每种氨基酸都具有多种理化性质,氨基酸的理化性质对蛋白质的结构和功能起着重要的作用。本文考虑氨基酸的10种理化性质:解离常数(pKa(NH3+)和pKa)、等电点(pI)、相对分子质量(Mw)、旋光率([a]D(H2O)和[a]D(HCl))、极性需求(Pr)、侧链的化学成分(Cc)、疏水值(Hb)和侧链质量(Scm),具体数值见表 1。
| 表 1 氨基酸的10种理化性质 Table 1 10 physicochemical properties of amino acids |
为消除量纲不一的影响,先对10组氨基酸理化性质进行标准化处理,将其化为均值为0,标准差为1的数据框。然后对该20×10的氨基酸理化性质矩阵进行主成分分析,将10组变量的信息压缩为几个综合变量,提取有效的主成分来表示20种天然氨基酸的理化性质。主成分分析结果见表 2。
| 表 2 重要主成分的贡献率 Table 2 Contribution of significant principal components |
由表 2可以看到,前6个主成分的累计贡献率为95.91%,远大于85%,可以认为这6个主成分能代表原先10组理化性质的绝大部分信息。计算这6个主成分的得分,即把原来的20×10的氨基酸理化性质矩阵转化为20×6的主成分得分矩阵(见表 3)。
| 表 3 主成分得分矩阵 Table 3 Principal component score matrix |
对于任一长度为n的蛋白质序列S,计算蛋白质序列S的各主成分平均值
| $ \overline{P C_j}=\sum\limits_{i=1}^{20} \frac{n_i P C_{i j}}{n} \quad j=1, 2, \cdots, 6 $ | (1) |
其中Ω={A, R, N, D, C, Q, E, G, H, I, L, K, M, F, P, S, T, W, Y, V}, Ai(i=1, 2, …, 20)表示Ω中的第i个氨基酸,ni表示序列S中氨基酸Ai的数量,PCij表示氨基酸Ai的第j个主成分得分(见表 3)。对每条序列经计算可得到6维氨基酸主成分得分平均值向量
例如对于蛋白质序列MTMHTTMTTLTLTSL,nM=3, nT=7, nH=1, nL=3, nS=1,则
对于一条长度为n的蛋白质序列S=(s1, s2, …, sn),其中sj∈Ω, j=1, 2, …, n,还可以基于每种氨基酸Ai(i=1, 2, …, 20)的平均位置[19]构造一个20维的特征向量,如下所示:
| $ \mu_i=\frac{\sum\limits_{j=1}^n j \times I\left(s_j=A_i\right)}{n_i} $ | (2) |
其中ni表示对应氨基酸的数量,
利用上述构建的两组特征向量,对每条蛋白质序列,将6维氨基酸主成分得分平均值向量和20维氨基酸平均位置向量结合起来可以得到一个26维蛋白质序列的数值化向量表示
为验证本文所提方法的有效性,用三组蛋白质序列数据集[19-20]进行实验,利用欧氏距离计算两两蛋白质序列所对应的26维特征向量之间的距离,然后利用UPGMA算法(该算法已嵌入到MEGA11软件)构建生物系统进化树。
2.1 9物种ND5蛋白质序列9个物种的ND5蛋白质序列信息在表 4中给出。使用本文的方法,可以得到9物种ND5蛋白质序列的一个9×26特征矩阵,然后计算两两间的欧氏距离可以得到相似性距离矩阵,结果见表 5。
| 表 4 9物种ND5蛋白质序列信息 Table 4 Information on 9 ND5 protein sequences |
| 表 5 9物种ND5蛋白质序列相似性距离矩阵 Table 5 The similarity/dissimilarity matrix of 9 ND5 protein sequences |
观察表 5可以看出,普通黑猩猩和侏儒黑猩猩的相似性距离最小,为2.679,表示普通黑猩猩和侏儒黑猩猩间的亲缘关系最近;大鼠和负鼠的相似性距离最大,为9.976,表示大鼠和负鼠间亲缘关系最远。同时,可以看到,人类、普通黑猩猩、侏儒黑猩猩和大猩猩这四个物种间的相似性距离比较小,说明它们的蛋白质序列相似性程度高,进化关系上较为接近;长须鲸和蓝鲸间相似性距离也很小,说明它们的进化关系接近;负鼠和其他八个物种的相似性距离都很大,表明在进化关系上与其它物种相比负鼠相对比较独立。
进一步利用相似性距离矩阵构建物种进化树,结果如图 1所示。通过观察发现9个物种被分成4个分支:第1个分支是侏儒黑猩猩、普通黑猩猩、人类和大猩猩,在这一分支中,侏儒黑猩猩和普通黑猩猩进化关系更近,其次是人类,而后是大猩猩,这与进化事实相符合;第2个分支是蓝鲸和长须鲸;第3分支为大鼠和小鼠;第4个分支为负鼠,与其他物种进化关系较远,单独成一个分支。从进化关系上看,侏儒黑猩猩、普通黑猩猩、人类和大猩猩都属于灵长目人科,蓝鲸和长须鲸都属于鲸目须鲸科,大鼠和小鼠都属于啮齿目鼠科,负鼠属于负鼠目负鼠科,本文的分析结果与实际进化关系相一致。
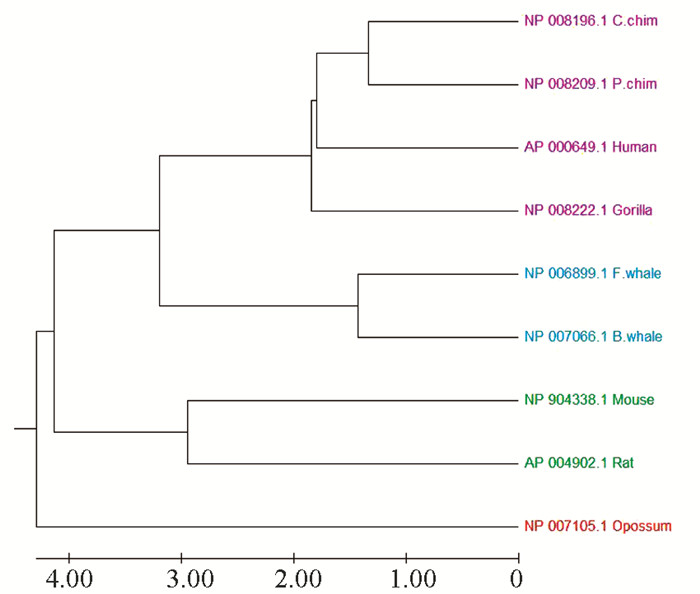
|
图 1 9物种ND5蛋白质序列的进化树 Figure 1 The phylogenetic tree of 9 ND5 protein sequences |
12个杆状病毒蛋白质序列信息见表 6,使用本文所提方法对其构建进化树,结果见图 2。由图 2可以看到,Alphabaculovirus病毒和Betabaculovirus病毒被分为两大分支,并且Alphabaculovirus中的Group Ⅰ和Group Ⅱ也都形成各自的分支,与实际的病毒进化关系一致。而文献[7]没有将Alphabaculovirus病毒和Betabaculovirus病毒形成两个大分支,并且Group Ⅱ中的6个病毒不在一个分支,HzSNPV、HaSNPV、HearNPV与Betabaculovirus病毒的进化距离要比与Group Ⅱ中的其他病毒的距离要小,这与实际的进化关系不一致。文献[8]和[20]虽然将Alphabaculovirus病毒和Betabaculovirus病毒形成了两个大分支,但是Group Ⅱ中的6个病毒并不在一个分支,Group Ⅰ中的AcMNPV、BmNPV、RoMNPV各自与Group Ⅱ中的三个病毒形成分支。
| 表 6 12个杆状病毒蛋白质序列信息 Table 6 Information on 12 Baculovirus protein sequences |

|
图 2 12个杆状病毒蛋白质序列的进化树 Figure 2 The phylogenetic tree of 12 baculovirus protein sequences |
甲型流感病毒的一些亚型是根据H(血凝素类型)的编号(H1到H18)和N(神经氨酸酶类型)的编号(N1到N11)来标记的,最致命的甲流亚型是H1N1、H2N2、H5N1、H7N3和H7N9,本文选取了35个与这些重要亚型相关的蛋白质序列。
使用我们的方法对该蛋白质序列数据集构建进化树,结果见图 3。由图 3可知,五种最致命的甲型流感病毒亚型H1N1、H2N2、H5N1、H7N3和H7N9各自形成5个分支,35个病毒都被正确聚类。相比之下,用ClustalW方法构建的进化树则有3个甲型流感病毒亚型聚类错误,如图 4所示,其中A/turkey/VA/505477-18/2007(H5N1),A/turkey/Ontario/FAV110-4/2009(H1N1)和A/turkey/Virginia/4135/2014(H1N1)没能正确被聚类。并且在同一台笔记本电脑下,ClustalW方法完成多序列比对需要花费约7 s,而我们的方法将序列转化为特征向量只需0.17 s。
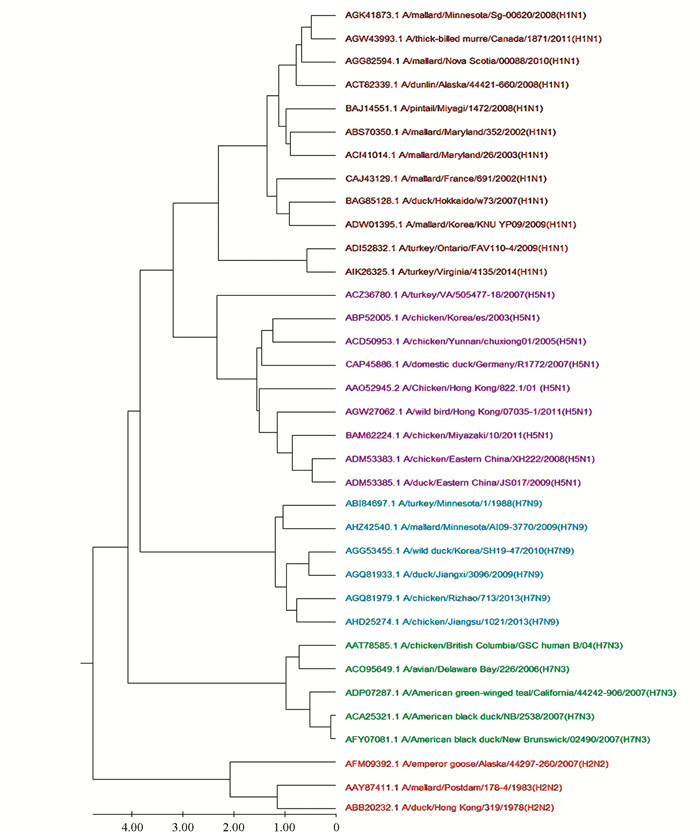
|
图 3 本文方法构建的35个甲型流感病毒蛋白质序列的进化树 Figure 3 The phylogenetic tree of 35 influenza A virus protein sequences constructed using our method |
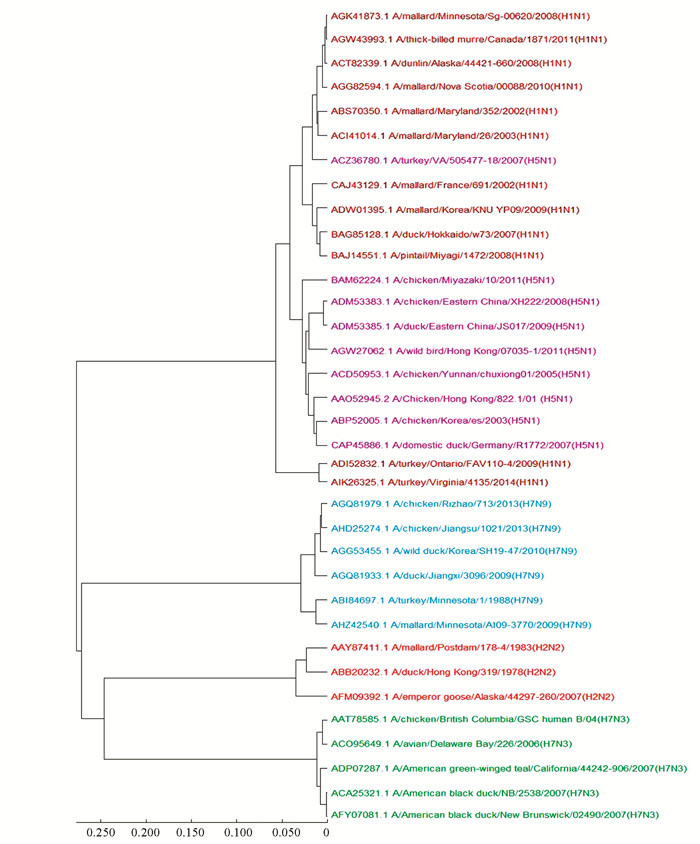
|
图 4 ClustalW方法构建的35个甲型流感病毒蛋白质序列的进化树 Figure 4 The phylogenetic tree of 35 influenza A virus protein sequences constructed using ClustalW |
新的非比对的蛋白质序列相似性分析的方法,将蛋白质序列转化为数值向量时,同时考虑了蛋白质序列中20种天然氨基酸的数量、理化性质和平均位置信息,最终将每条蛋白质序列都转化为唯一与之对应的26维特征向量。该新方法在3个数据集上均获得了准确的聚类结果,这说明该新方法在分析蛋白质序列的相似性方面是有效的。此外,该方法不需要复杂的计算,而且简便快捷。
| [1] |
KATOH K, MISAWA K, KUMA K, et al. MAFFT: A novel method for rapid multiple sequence alignment based on fast fourier transform[J]. Nucleic Acids Research, 2002, 30(14): 3059-3066. DOI:10.1093/nar/gkf436 (  0) 0) |
| [2] |
THOMPSON J D, GIBSON T J, HIGGINS D G. Multiple sequence alignment using clustalw and clustalx[J/OL]. Current Protocols in Bioinformatics, (2002-08-01)[2022-09-10]. https://doi.org/10.1002/0471250953.bi0203s00. DOI: 10.1002/0471250953.bi0203s00.
(  0) 0) |
| [3] |
ROBERT C, EDGAR. MUSCLE: Multiple sequence alignment with high accuracy and high throughput[J]. Nucleic Acids Research, 2004, 32(5): 1792-1797. DOI:10.1093/nar/gkh340 (  0) 0) |
| [4] |
VINGA S, ALMEIDA J. Alignment-free sequence comparison—a review[J]. Bioinformatics, 2003, 19: 513-523. DOI:10.1093/bioinformatics/btg005 (  0) 0) |
| [5] |
张艳萍, 贺平安. 蛋白质序列的图形表示及其应用[J]. 浙江理工大学学报, 2010, 27(2): 308-314. ZHANG Yanping, HE Ping-an. Graphical representation of protein sequences and its applications[J]. Journal of Zhejiang Sci-Tech University, 2010, 27(2): 308-314. DOI:10.3969/j.issn.1673-3851.2010.02.029 (  0) 0) |
| [6] |
潘以红, 钱东, 朱平. 蛋白质序列图形变换及其相似性聚类分析[J]. 生命科学研究, 2018, 22(3): 191-200. PAN Yihong, QIAN Dong, ZHU Ping. Graphical transformation and similarity clustering analysis for protein sequences[J]. Life Science Research, 2018, 22(3): 191-200. DOI:10.16605/j.cnki.1007-7847.2018.03.003 (  0) 0) |
| [7] |
YAO Yuhua, YAN Shoujiang, XU Huimin, et al. Similarity/dissimilarity analysis of protein sequences based on a new spectrum-like graphical representation[J]. Evolutionary Bioinformatics, 2014, 10(1): 87-96. DOI:10.4137/EBO.S14713 (  0) 0) |
| [8] |
HOU Wenbing, PAN Qiuhui, HE Mingfeng. A new graphical representation of protein sequences and its applications[J]. Physica A Statistical Mechanics & Its Applications, 2016, 444: 996-1002. DOI:10.1016/j.physa.2015.10.067 (  0) 0) |
| [9] |
HE Pingan, XU Suning, DAI Qi, et al. A generalization of CGR representation for analyzing and comparing protein sequences[J]. International Journal of Quantum Chemistry, 2016, 116(6): 476-482. DOI:10.1002/qua.25068 (  0) 0) |
| [10] |
JIE L, KOEHL P. 3D representations of amino acids—applications to protein sequence comparison and classification[J]. Computational and Structural Biotechnology Journal, 2014, 11(18): 47-58. DOI:10.1016/j.csbj.2014.09.001 (  0) 0) |
| [11] |
HU Hailong, LI Zhong, DONG Hongwei, et al. Graphical representation and similarity analysis of protein sequences based on fractal interpolation[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2017, 14(1): 182-192. DOI:10.1109/TCBB.2015.2511731 (  0) 0) |
| [12] |
AGATA C, DOROTA B W, PIOTR W, et al. 20D-dynamic representation of protein sequences[J]. Genomics, 2016, 107: 16-23. DOI:10.1016/j.ygeno.2015.12.003 (  0) 0) |
| [13] |
CHOU K C. Some remarks on protein attribute prediction and pseudo amino acid composition[J]. Journal of Theoretical Biology, 2011, 273(1): 236-247. DOI:10.1016/j.jtbi.2010.12.024 (  0) 0) |
| [14] |
CHEN Wei, LIN Hao, CHOU Kuochen. Pseudo nucleotide composition or PseKNC: an effective formulation for analyzing genomic sequences[J]. Molecular BioSystems, 2015, 11(10): 2620-2634. DOI:10.1039/c5mb00155b (  0) 0) |
| [15] |
贾美多, 杨闫, 张盈盈, 等. 蛋白质序列基于k-字的数值刻画及应用[J]. 浙江农业学报, 2014, 26(6): 1635-1640. JIA Meiduo, YANG Yan, ZHANG Yingying, et al. Numerical k-word based portrayal of protein sequences and applications[J]. Acta Agriculturae Zhejiangensis, 2014, 26(6): 1635-1640. DOI:10.3969/j.issn.1004-1524.2014.06.40 (  0) 0) |
| [16] |
XIE Xianhua, YU Zuguo, HAN Guosheng, et al. Whole-proteome based phylogenetic tree construction with inter-amino-acid distances and the conditional geometric distribution profiles[J]. Molecular Phylogenetics and Evolution, 2015, 89: 37-45. DOI:10.1016/j.ympev.2015.04.008 (  0) 0) |
| [17] |
LI Yushuang, SONG Tian, YANG Jiasheng, et al. An Alignment-Free Algorithm in Comparing the Similarity of Protein Sequences Based on Pseudo-Markov Transition Probabilities among Amino Acids[J]. PLoS ONE, 2016, 11(12): e0167430. DOI:10.1371/journal.pone.0167430 (  0) 0) |
| [18] |
LI Yongkun, TIAN Kun, YIN Changchuan, et al. Virus classification in 60-dimensional protein space[J]. Molecular Phylogenetics and Evolution, 2016, 99: 53-62. DOI:10.1016/j.ympev.2016.03.009 (  0) 0) |
| [19] |
HE L, LI Y, HE R L, et al. A novel alignment-free vector method to cluster protein sequences[J]. Journal of Theoretical Biology, 2017, 427: 41-52. DOI:10.1016/j.jtbi.2017.06.002 (  0) 0) |
| [20] |
朱臣臣, 赵熙强. 基于氨基酸的理化性质和位置信息的蛋白质序列相似性分析方法[J]. 中国海洋大学学报, 2021, 51(增Ⅰ): 95-100. ZHU Chenchen, ZHAO Xiqiang. Similarity/dissimilarity analysis of protein sequence based on physicochemical properties and position information of amino acids[J]. Periodical of Ocean University of China (Natural Science Edition), 2021, 51(Sup.Ⅰ): 95-100. DOI:10.16441/j.cnki.hdxb.20190110 (  0) 0) |
| [21] |
YAU S S T, YU C, HE R. A protein map and its application[J]. DNA and Cell Biology, 2008, 27(5): 241-250. DOI:10.1089/dna.2007.0676 (  0) 0) |
| [22] |
DAI Qi, YANG Yanchun, WANG Tianming. Markov model plus k-word distributions: a synergy that produces novel statistical measure for sequence comparison[J]. Bioinformatics, 2008, 24(20): 2296-2302. DOI:10.1093/bioinformatics/btn436 (  0) 0) |
| [23] |
LIU Yufeng, ZENG Jianyang, GONG Haipeng. Improving the orientation-dependent statistical potential using a reference state[J]. Proteins, 2014, 82(10): 2383-2393. DOI:10.1002/prot.24600 (  0) 0) |
| [24] |
SALICHOS L, ROKAS A. Inferring ancient divergences requires genes with strong phylogenetic signals[J]. Nature, 2013, 497: 327-331. DOI:10.1038/nature12130 (  0) 0) |
| [25] |
WIMLEY W C, WHITE S H. Experimentally determined hydrophobicity scale for proteins at membrane interfaces[J]. Nature Structural Biology, 1996, 3: 842-848. DOI:10.1038/nsb1096-842 (  0) 0) |
 2023, Vol. 21
2023, Vol. 21


