能量是控制神经元生物物理学机制和神经活动的基础,神经系统的信息处理离不开大量能量的消耗[1-2]。研究表明静息状态下人脑能量消耗占全身的20%,工作状态下占40%,其中信号传递占大脑皮层总能量消耗的80%[3]。这种能量需求大到足以影响人类大脑的设计、功能与进化[4]。在非人类的大脑中能量也能影响大脑功能,例如在小鼠缺氧暴露试验中就观察到锥体神经元的突触阻滞现象与空间记忆缺陷[5]。更进一步地,有研究表明在具有梯度电位和脉冲的神经元中,信噪比、胞体响应速度以及离子通道的数量等方面都与能量有密切关联[6-7]。提高信噪比需要额外的能量,因为可靠性随着用于产生信号的随机事件数而增加。提高带宽也需要额外的能量,因为增加电导来降低膜时间常数会导致单位时间内需要更强的刺激才能唤起胞体脉冲[6]。改变离子通道数量也需要额外的能量支持,增加钾离子通道或减少钠离子通道后,神经元需要消耗更多能量来产生胞体脉冲[7]。由于信噪比、响应速度以及离子通道数量等因素的改变都与电导的变化密切相关,而电导的改变意味着突触权重发生变化,因此能量也是突触权重变化的基础。
能量是影响突触权重变化的关键因素。首先,能量影响突触前的信息传递。能量不仅可以驱动突触囊泡周期,而且能通过调节突触囊泡周期的速度来改变囊泡释放概率,从而影响突触后权重变化[8-9]。其次,能量约束离子通道动力学以及离子通道数量。由于树突整合是神经元信息处理过程中主要且昂贵的代谢步骤[10],离子通道的任何变化都可能导致其能量消耗的波动[11],因此能量的上限限制了离子通道的精确类型及其密度[12-13]。综上所述,能量是突触权重变化的关键因素,给出能量与突触权重的函数关系是具有价值的。
为系统解释突触范围内能量的变化与突触可塑性的关系,利用Brian2[14]神经元模拟器构建一个基于能量的突触可塑性模型。该模型的突触权重变化方向与幅度取决于正离子进入突触后膜的瞬时功率。当瞬时功率超过动态功率阈值时突触权重增长,反之突触权重下降,增长与下降的幅度由瞬时功率的幅度决定。为检验能量模型是否能够解释脉冲频率依赖可塑性以及脉冲时间依赖可塑性这两种最主要的突触可塑性,用能量模型复现Sjöström等[15]在小鼠视皮层第5层锥体神经元上进行的突触可塑性实验。在此基础上,将能量模型与电压依赖突触可塑性模型以及脉冲时刻依赖(Spike-timing dependent plasticity, STDP)突触可塑性模型进行比较。
1 方法 1.1 基于能量的突触可塑性模型建模使用Python进行网络仿真,并采用Bono与Clopath基于Brian2[14]开发的详细生物物理学神经元模型对小鼠视皮层第5层锥体神经元进行模拟[16]。该神经元由1 181个隔室组成,每一个隔室均包含泄露电流、电压门控型钠离子通道、延迟整流型钾离子通道、高阈值钙离子通道与低阈值钙离子通道,能够模拟树突、轴突和胞体在接受外界刺激时的膜电位变化过程。突触部分包含α-氨基-3-羟基-5-甲基-4-异恶唑丙酸(α-Amino-3-hydroxy-5-Methyl-4-isoxazole-Propionic Acid, AMPA)受体与N-甲基-D-天冬氨酸(N-methyl-D-aspartic Acid, NMDA)受体,并且具有突触可塑性,即在外界刺激的情况下,受体的电导可以发生较为持久的变化,也就是突触权重可以发生持久改变。此处的突触权重指的是,在突触受到刺激时突触后膜受体通道的电导瞬时值与电导最大值的比值。具体公式如下所示:
| $g(t)=w(t) \times g_{\max }$ | (1) |
式(1)中,g(t)是突触激活时突触后膜AMPA与NMDA受体的瞬时电导之和,w(t)是突触权重,gmax是AMPA与NMDA受体的最大电导之和。突触刺激后AMPA与NMDA受体的电导会依据各自的时间常数指数衰减到零。
在能量模型中突触权重与能量的关系是,当电流进入突触后膜的瞬时功率Pm(t)大于可变功率阈值Pth(t)时突触权重增加,反之突触权重减少。这是因为在动作电位上升阶段,突触刺激导致AMPA受体、NMDA受体以及其他电压门控离子通道开放,神经元外部大量的正离子通过这些离子通道顺浓度梯度进入突触后膜,使得突触后膜的瞬时功率迅速上升,当Pm(t)>Pth(t)时,会导致肌动蛋白细胞骨架和膜动力学改变,使得树突棘结构和功能的改变,诱发长时程增强(Long Term Potentiation, LTP)[17],突触权重上升。在动作电位下降阶段,由于神经元内的电势能较高,导致细胞膜内外电势差较静息状态时更小,加之钠钾泵消耗能量向细胞膜内外转运正离子,因此电流涌入突触后膜的瞬时功率逐渐衰减,当Pm(t) < Pth(t)之后,会诱发长时程抑制(Long Term Depression, LTD)[18-19],突触权重下降。突触权重的变化用公式表达如下:
| $w(t)=\left(P_{\mathrm{th}}(t)>\theta\right) \times A(t) \times P_{\mathrm{m}}(t)$ | (2) |
式中,Pm(t)为突触后膜的瞬时功率,可变幅值A(t)与功率阈值Pth(t)都是功率Pm(t)的函数(见公式(4)~(8)),θ为权重变化阈值,取值为0.8 nW,因此突触权重的变化量w(t)是功率Pm(t)的函数。需要说明的是,突触权重只有在功率阈值Pth(t)>θ时才发生改变,这是因为只有刺激达到一定水平才能够激活突触,并且诱发突触形态和功能的改变[20-21]。
式中,突触后膜局部范围内瞬时功率Pm(t)的计算公式如下:
| $P_{\mathrm{m}}(t)=I_{\text {post }}(t) \times V_{\text {post }}(t) \times S$ | (3) |
式中,Ipost(t)为突触后膜单位面积流入的电流,Vpost(t)为突触后局部膜电位,这两者皆可由Brian2内置的状态检测器直接测出。S为突触所在隔室的面积,具体参数请查阅参考文献16。
功率阈值Pth(t)是瞬时功率Pm(t)经过低通滤波后的功率:
| $\tau \frac{d P_{\mathrm{th}}(t)}{d t}=\left(P_{\mathrm{m}}(t)-P_{\mathrm{th}}(t)\right)$ | (4) |
式中,τ为低通滤波的时间常数,其计算公式如下所示:
| $\tau=(36-36 \times w(t))$ | (5) |
低通滤波的时间常数τ由突触权重w(t)决定。突触权重越高,低通滤波时间常数τ越小,功率阈值Pth(t)越接近瞬时功率Pm(t),需要更高频率或更大幅度的电流刺激才能使瞬时功率Pm(t)超过功率阈值Pth(t)。(5)式中的参数由尝试法求得。
式(2)中,可变幅值A(t)的公式如下所示:
| $\begin{gathered}A(t)=A_{\mathrm{ltp}}(t) \times\left(P_{\mathrm{m}}(t)-P_{\mathrm{th}}(t)\right)_{+}+ \\ A_{\mathrm{ltd}}(t) \times\left(P_{\mathrm{m}}(t)-P_{\mathrm{th}}(t)\right)_{-}\end{gathered}$ | (6) |
式中,Altp(t)与Altd(t)分别为突触增强与减弱时的可变幅值。公式(Pm(t)-Pth(t))+在Pm(t)>Pth(t)时等于1,反之等于0。(Pm(t)-Pth(t))-则与之相反。突触权重增强与减弱的幅值不同是符合生物实验[22]。Altp(t)与Altd(t)都是功率阈值Pth(t)的函数:
| $A_{\text {ltp }}(t)=20.7 \times e^{-6 \times P_{\mathrm{th}}(t)}+1.4$ | (7) |
| $A_{\mathrm{ltd}}(t)=-16 \times e^{-6 \times P_{\mathrm{th}}(t)}$ | (8) |
从方程式(6)~(8)中可以看出可变幅值A(t)与功率阈值Pth(t)有关,由于功率阈值Pth(t)是瞬时功率Pm(t)的函数,所以可变幅值A(t)也是瞬时功率Pm(t)的函数。
突触权重的上升幅度Altp(t)与功率阈值Pth(t)呈指数关系的原因在于,如果突触后神经元接受单脉冲刺激,由于突触小泡中释放的谷氨酸分子数量远大于突触后膜受体的数量,因此单脉冲刺激会激活突触后膜的大部分离子通道[23],导致电流流入神经元的瞬时功率大幅度升高,使得突触权重的上升幅度Altp(t)随功率阈值Pth(t)的升高而线性上升。如果突触后神经元接受的是高频脉冲刺激,谷氨酸结合位点逐渐接近饱和[24-25],突触后膜离子通道的电导也接近最大值,此时虽然功率阈值Pth(t)仍在上升,但突触权重的上升幅度Altp(t)会趋向一个固定值。
突触权重的下降幅度Altd(t)与功率阈值Pth(t)呈指数关系的原因在于,在突触刺激刚消失时,突触后膜电位向静息电位衰减,由于大部分离子通道仍保持开放状态,外界的正离子还在通过离子通道进入神经元内部,因此电流流入神经元的瞬时功率Pm(t)仅仅略低于功率阈值Pth(t),且功率阈值Pth(t)保持在较高水平,此时随着功率阈值Pth(t)的下降,突触权重的下降幅度Altd(t)仍然接近0。当突触后膜电位衰减至静息电位时,突触后膜的离子通道逐步关闭,此时随着功率阈值Pth(t)的降低,突触权重的下降幅度Altd(t)也增大。
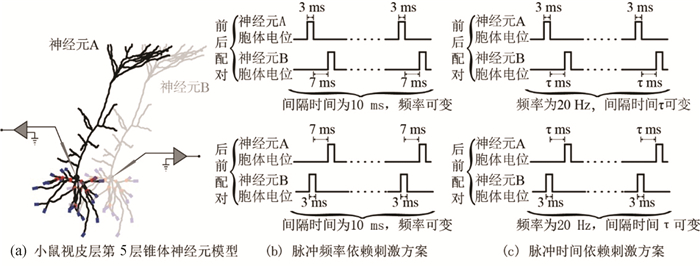
1.2 检验突触可塑性的刺激方案为证明能量是决定突触可塑性的关键因素,构建两个生物物理学神经元模型(见图 1a),红点与蓝点分别表示基底树突近端与远端突触位点,并仿照Sjöström等[15]的生物实验设计以下两种刺激方案。
|
图 1 神经元连接及刺激方案示意图 Figure 1 Schematic diagram of neuron connection and stimulation scheme |
脉冲频率依赖刺激方案(见图 1b)。为检验能量模型能否复现脉冲频率依赖的突触可塑性,将两个神经元的基底树突近端或远端通过单个突触相互连接,分别向两个神经元的胞体注入3 ms的1 000 pA电流,从而唤起相同频率的胞体脉冲(0.1、10、20、30、40和50 Hz),每一种频率下唤起的胞体脉冲总数都为60个。在前—后配对时,突触前神经元每一个胞体脉冲的起始时间都比突触后神经元的提前10 ms,后—前配对则相反。突触权重初始值设为0.5。该刺激方案分别在树突近端与远端重复10次,每一次均重新选取突触位置。利用Brian2内含的状态检测器来检测突触权重与突触后膜瞬时功率的变化,得到图 2a~2f。图 2a与2d的阴影部分表示一个标准差的范围。
|
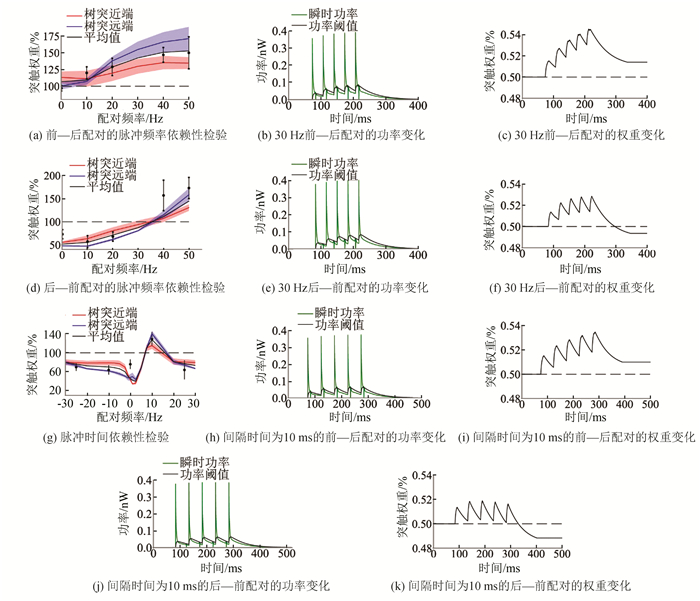
图 2 脉冲频率以及脉冲时间依赖可塑性检验 Figure 2 Pulse frequency and pulse time dependent plasticity test |
脉冲时间依赖刺激方案(见图 1c)。为检验能量模型能否复现脉冲时间依赖的突触可塑性,将两个神经元的基底树突近端或远端通过单个突触相互连接,通过向胞体注入3 ms的1 000 pA电流的方式,在两个神经元上都唤起频率为20 Hz的胞体脉冲,2个神经元胞体脉冲起始时间之间具有时间差(1、2.5、5、7.5、10、20和30 ms),并统计60次脉冲后突触权重的变化。前—后配对时突触前神经元先释放一个胞体脉冲,在经过间隔时间(1、2.5、5、7.5、10、20和30 ms)后突触后神经元释放一个胞体脉冲。后—前配对则相反。突触初始权重为0.5。该刺激方案分别在树突近端与远端重复10次,每次都重新选取突触位置。用状态监测器记录突触权重变化与突触后膜瞬时功率的变化,得到图 2g~2k。图 2g的阴影部分表示一个标准差的范围。
2 结果 2.1 突触可塑性检验为研究能量模型是否能复现脉冲频率依赖可塑性,将两个生物物理学神经元相连接,采用Sjöström等[15]设计的脉冲频率依赖刺激方案。图 2a展示了在前后-配对的脉冲频率刺激方案下,突触权重随配对频率的变化。红线与蓝线分别是树突近端与远端的突触响应平均值,阴影部分代表一个标准差的范围。误差棒表示Sjöström等[15]通过生物实验得到的误差范围,黑色实线是所有突触的响应平均值,虚线是初始权重0.5。可以看出,在前—后配对时,无论突触位于基底树突近端还是远端,刺激频率越大,突触前神经元连接至突触后神经元的突触权重的上升幅度也越大,并且刺激后突触权重的平均值都落在生物实验的误差范围内。这是因为在突触刺激与突触后神经元的胞体脉冲共同作用下,突触后神经元的离子通道打开,大量正离子顺离子浓度梯度进入突触后膜,导致注入突触后膜的电流增大,由于突触后膜的瞬时功率等于进入突触后膜的瞬时电流乘以细胞膜的电位差,因此突触后膜的瞬时功率上升。当瞬时功率Pm(t)高于功率阈值Pth(t)时,突触上的肌动蛋白细胞骨架和膜动力学发生改变,突触权重上升[17]。
图 2b与2c进一步解释了在脉冲频率依赖刺激方案中以30 Hz进行前—后配对时,突触后膜的瞬时功率Pm(t)与突触权重w(t)随时间变化的关系。图 2b的绿线是突触后膜的瞬时功率Pm(t),黑线是功率阈值Pth(t)。由图 2b与2c可知,在0至60 ms时,由于没有电流刺激,功率阈值Pth(t)低于权重变化阈值θ,突触权重不发生改变。在60 ms至70 ms阶段,在突触刺激与突触后神经元胞体脉冲共同作用下,突触后膜的瞬时功率Pm(t)高于功率阈值Pth(t),导致突触权重上升。在70 ms~110 ms阶段,由于离子通道逐渐关闭,Pm(t) < Pth(t),突触权重下降,由于下降的幅度小于上升的幅度,因此在重复5次配对刺激后,突触权重从初始值0.5上升到0.515。
脉冲频率依赖刺激方案的后—前配对结果如图 2d所示。由图可见如果两个神经元的胞体脉冲频率相同且突触前神经元的胞体脉冲比突触后神经元落后10 ms,无论突触位于基底树突的近端或远端,突触前神经元连接至突触后神经元的突触权重在刺激频率小于35 Hz时都会下降,只有在刺激频率大于35 Hz时才会逐步上升。这是因为突触后神经元在胞体脉冲后进入去火期,在此期间进行突触刺激只能打开少许突触后膜的离子通道,引起少量正离子流入,即突触后膜的瞬时功率Pm(t)低于功率阈值Pth(t),所以无法引起突触权重的改变甚至会导致诱导LTD。
图 2e与2f进一步展示了在脉冲频率依赖刺激方案中以30 Hz进行后—前配对时,突触后膜的瞬时功率Pm(t)与突触权重w(t)变化的关系。在60 ms之前,由于没有突触刺激与胞体脉冲,突触后膜的瞬时功率Pm(t)为零,突触权重无变化。在60 ms时,突触后神经元产生胞体脉冲,但由于树突棘颈部的电阻很大,削弱了胞体脉冲的影响,因此突触后膜只有极少量离子通道打开,瞬时功率Pm(t)与功率阈值Pth(t)几乎没变化,突触权重也不改变。在70 ms时,突触刺激引起突触后膜大量离子通道打开,瞬时功率Pm(t)高于功率阈值Pth(t),突触权重上升,但由于没有诱发突触后神经元的胞体脉冲,在突触刺激撤去后突触权重持续下降,在重复5次配对刺激后,突触权重从初始值0.5下降到0.495。
其次,为研究能量模型是否能复现脉冲时间依赖可塑性,对能量模型采用Sjöström等[15]设计的脉冲时间依赖刺激方案。由图 2g可见,只有在采取前—后配对且脉冲时间间隔在10 ms左右时突触权重增加,在后—前配对时突触权重的变化量为负值。随着间隔时间的增大,无论是前—后配对还是后—前配对,突触权重的变化量都趋于0。这是因为在后—前配对时,突触后神经元的胞体脉冲始终先于突触刺激,由于胞体脉冲持续时间较短(1~2 ms)[26],因此两者无法相互叠加,导致突触后膜的离子通道只有少量开放,瞬时功率Pm(t)低于功率阈值Pth(t),导致LTD。在前—后配对时,由于突触刺激持续时间较长,突触后神经元的胞体脉冲与突触刺激能够同时作用在离子通道上,使得大量正离子进入突触后膜,瞬时功率Pm(t)高于功率阈值Pth(t),导致LTP。当间隔时间超过20 ms后,无论是前—后配对还是后—前配对,突触刺激和胞体脉冲对离子通道的作用都无法叠加,瞬时功率Pm(t)始终低于功率阈值Pth(t)且接近于0,因此突触权重的改变量为负值并且趋向0。
图 2h~2k分别展示了在脉冲时间依赖刺激方案中胞体脉冲间隔时间为+10 ms与-10 ms时,突触后膜的瞬时功率Pm(t)与突触权重w(t)随时间的变化关系。由图 2h与2i可知,当脉冲间隔时间为+10 ms时,在60 ms~70 ms,突触后神经元产生胞体脉冲与突触刺激共同诱导大量离子通道开放,瞬时功率Pm(t)高于功率阈值Pth(t),重复5次配对后突触权重上升到0.509。图 2j与2k则显示当脉冲间隔时间为-10 ms时,在60 ms突触后神经元产生胞体脉冲,但由于没有与突触刺激相配对,因此瞬时功率Pm(t)很小,权重无变化。在70 ms时突触刺激使瞬时功率Pm(t)上升,由于没唤起突触后神经元的动作电位,因此突触刺激消失后Pm(t)长时间低于功率阈值Pth(t),重复刺激5次后突触权重最终下降到0.488。
2.2 模型比较为了证明基于能量的突触可塑性模型与其他模型相比具有优越性,比较能量模型、电压依赖可塑性模型[16]以及STDP模型[27]在脉冲频率依赖可塑性实验和脉冲时间依赖可塑性实验中的响应,以Sjöström等生物实验的误差范围[15]作为评判模型优越性的标准。
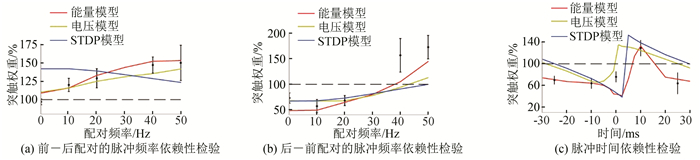
图 3a与3b显示了三种突触可塑性模型在脉冲频率依赖可塑性实验下的响应,其中红线、黄线与蓝线分别表示能量模型、电压模型与STDP模型在基底树突近端与远端的突触响应平均值,误差棒表示Sjöström等[15]通过生物实验得到的误差范围,黑色虚线是初始权重0.5。由图 3a可知,在前—后配对情况下,能量模型与电压模型的响应仅在刺激频率接近0 Hz时略高于生物实验的平均值,在其余刺激频率下都与生物实验的平均值相似。相比之下,STDP模型的响应只在刺激频率大于20 Hz时落在误差范围内,在低频刺激下都落在误差范围外。再由图 3b可知,在后—前配对的情况下,电压模型与STDP模型的响应在低频段(≤20 Hz)都贴合实验值,在高频段(>20 Hz)两个模型的响应远离实验数据。与之相比,能量模型的响应在刺激频率为0 Hz时离误差值较远,但在高频段更接近生物实验的误差范围。图 3a与3b共同证明了在脉冲频率依赖可塑性的实验条件下,能量模型相较公认的电压依赖可塑性模型以及传统的STDP模型更具有优越性。
|
图 3 模型对比分析 Figure 3 Model comparison analysis |
其次,对比脉冲时间依赖可塑性实验的结果(见图 3c),红线、黄线、蓝线以及误差棒的意义与图 3a与2b相同。由图可见,能量模型的响应仅在间隔时间接近0 ms时低于实验值,在间隔时间大于或小于0 ms时都处在误差范围内。而电压模型和STDP模型的响应只在间隔时间等于-10 ms或10 ms时贴合实验值,其余部分均不在误差范围内。因此证明在脉冲时间依赖可塑性的实验条件下,能量模型同样具有优越性。
3 结论与其他的突触可塑性模型相比,本文提出的基于能量的突触可塑性模型有两个主要优势。第一点是明确了能量是影响突触可塑性的关键因素。影响功能连接模式的因素众多,为解释生物实验中观察到的突触可塑性,部分模型将多种因素纳入考虑[16, 27-29],例如STDP模型[27]就需要考虑突触前和突触后两个神经元的脉冲间隔。相比之下,我们构建的突触可塑性模型仅通过对突触后范围内能量变化的分析,就能够再现脉冲频率依赖与脉冲时间依赖的突触可塑性,并且比电压依赖的突触可塑性模型[16]和经典的STDP模型[27]更贴合真实生物实验的结果。第二点是能量模型能够从生物物理学角度定量解释突触权重变化的过程。目前较为流行的STDP模型[27]、Hebbian模型[28]以及BCM模型[29]都只是描述神经元脉冲响应这一现象与突触权重之间的关联,并不涉及神经元内在的变化。而能量模型则是根据突触范围内的能量变化解释突触权重变化的过程,具有生物物理意义。
能量模型证明能量是解释突触可塑性的关键所在,这加深了我们对突触可塑性机制的理解,为学习和记忆的进一步研究提供了一个新的思路。接下来还可以从两方面对能量模型进行改进。首先,该模型虽然通过采用可变功率阈值Pth(t)的方式来避免硬边界设计,但在持续接受不符合生物实际的高频刺激时,突触权重有可能超出正常范围。第二,该模型的突触权重在瞬时功率与功率阈值都回归静息状态后就维持在一个定值。而在真实的神经元中,突触长时间未接受刺激时,其突触权重应该随时间逐渐衰减。可以考虑添加其他机制来模拟这个过程。
| [1] |
YU L, YU Y. Energy-efficient neural information processing in individual neurons and neuronal networks[J]. Journal of Neuroence Research, 2017, 95(11): 2253-2266. DOI:10.1002/jnr.24131 (  0) 0) |
| [2] |
HASENSTAUB A R, OTTE S, CALLAWAY E M, et al. Metabolic cost as a unifying principle governing neuronal biophysics[J]. Proceedings of the National Academy of Sciences of the United States of America, 2010, 107(27): 12329-12334. DOI:10.1073/pnas.0914886107 (  0) 0) |
| [3] |
ATTWELL D, LAUGHLIN S B. An energy budget for signaling in the grey matter of the brain[J]. Journal of Cerebral Blood Flow & Metabolism, 2001, 21(10): 1133-1145. DOI:10.1097/00004647-200110000-00001 (  0) 0) |
| [4] |
WATTS M E, ROGER P, CHARLES C. Brain energy and oxygen metabolism: emerging role in normal function and disease[J]. Frontiers in Molecular Neuroence, 2018, 11(216): 1-13. DOI:10.3389/fnmol.2018.00216 (  0) 0) |
| [5] |
YU Y, HERMAN P, ROTHMAN D L, et al. Evaluating the gray and white matter energy budgets of human brain function[J]. Journal of Cerebral Blood Flow & Metabolism, 2017, 38(8): 1339-1353. DOI:10.1177/0271678X17708691 (  0) 0) |
| [6] |
LAUGHLIN S B. Energy as a constraint on the coding and processing of sensory information[J]. Current Opinion in Neurobiology, 2001, 11(4): 475-480. DOI:10.1016/s0959-4388(00)00237-3 (  0) 0) |
| [7] |
LIU Y, YUE Y, YU Y, et al. Effects of channel blocking on information transmission and energy efficiency in squid giant axons[J]. Journal of Computational Neuroscience, 2018, 44(2): 219-231. DOI:10.1007/s10827-017-0676-2 (  0) 0) |
| [8] |
YUAN Y, HUO H, FANG T. Effects of metabolic energy on synaptic transmission and dendritic integration in pyramidal neurons[J]. Frontiers in Computational Neuroscience, 2018, 12(79): 1-13. DOI:10.3389/fncom.2018.00079 (  0) 0) |
| [9] |
RANGARAJU V, CALLOWAY N, RYAN T A, et al. Activity-driven local atp synthesis is required for synaptic function[J]. Cell, 2014, 156(4): 825-835. DOI:10.1016/j.cell.2013.12.042 (  0) 0) |
| [10] |
YUAN Y, HUO H, ZHAO P, et al. Constraints of metabolic energy on the number of synaptic connections of neurons and the density of neuronal networks[J]. Frontiers in Computational Neuroscience, 2018, 12(91): 1-13. DOI:10.3389/fncom.2018.00091 (  0) 0) |
| [11] |
OYARZABAL A, MARIN-VALENCIA I. Synaptic energy metabolism and neuronal excitability, in sickness and health[J]. Journal of Inherited Metabolic Disease, 2019, 42(2): 220-236. DOI:10.1002/jimd.12071 (  0) 0) |
| [12] |
NIVEN J E, LAUGHLIN S B. Energy limitation as a selective pressure on the evolution of sensory systems[J]. The Journal of Experimental Biology, 2008, 211(11): 1792-1804. DOI:10.1242/jeb.017574 (  0) 0) |
| [13] |
KOSTAL L, SHINOMOTO S. Efficient information transfer by Poisson neurons[J]. Mathematical Biosciences and Engineering, 2017, 13(3): 509-520. DOI:10.3934/mbe.2016004 (  0) 0) |
| [14] |
GOODMAN D. Brian: A simulator for spiking neural networks in Python[J]. Frontiers in Neuroinformatics, 2008, 2(5): 1-10. DOI:10.3389/neuro.11.005.2008 (  0) 0) |
| [15] |
SJÖSTRÖM P J, TURRIGIANO G G, NELSON S B. Rate, timing, and cooperativity jointly determine cortical synaptic plasticity[J]. Neuron, 2001, 32(6): 1149-1164. DOI:10.1016/s0896-6273(1)00542-6 (  0) 0) |
| [16] |
BONO J, CLOPATH C. Modeling somatic and dendritic spike mediated plasticity at the single neuron and network level[J]. Nature Communications, 2017, 8(1): 1-17.706. DOI:10.1038/s41467-017-00740-z (  0) 0) |
| [17] |
SREETAMA B, RAPHAEL L. The role of actin cytoskeleton in dendritic spines in the maintenance of long-term memory[J]. Frontiers in Molecular Neuroscience, 2018, 11(143): 1-9. DOI:10.3389/fnmol.2018.00143 (  0) 0) |
| [18] |
YASUDA R. Biophysics of biochemical signaling in dendritic spines: implications in synaptic plasticity[J]. Biophysical Journal, 2017, 113(10): 2152-2159. DOI:10.1016/j.bpj.2017.07.029 (  0) 0) |
| [19] |
PENNY C J, GOLD M G. Mechanisms for localising calcineurin and CaMKⅡ in dendritic spines[J]. Cellular Signal, 2018, 49(1): 46-58. DOI:10.1016/j.cellsig.2018.05.010 (  0) 0) |
| [20] |
WANG H X, GERKIN R C, NAUEN D W, et al. Coactivation and timing-dependent integration of synaptic potentiation and depression[J]. Nature Neuroscience, 2005, 8(2): 187-193. DOI:10.1038/nn1387 (  0) 0) |
| [21] |
LETZKUS J J, KAMPA B M, STUART G J. Learning rules for spike timing-dependent plasticity depend on dendritic synapse location[J]. Journal of Neuroscience, 2006, 26(41): 10420-10429. DOI:10.1523/JNEUROSCI.2650-06.2006 (  0) 0) |
| [22] |
OZCAN A S, OZCAN M S. Population dynamics and long-term trajectory of dendritic spines[J]. Frontiers in Synaptic Neuroscience, 2018, 10(25): 1-10. DOI:10.3389/fnsyn.2018.00025 (  0) 0) |
| [23] |
SINGH D, BHALLA U S. Subunit exchange enhances information retention by CaMKⅡ in dendritic spines[J]. Elife, 2018, 12(7): 1-22. DOI:10.7554/eLife.41412 (  0) 0) |
| [24] |
MAINEN Z F, MALINOW R, SVOBODA K. Synaptic calcium transients in single spines indicate that NMDA receptors are not saturated[J]. Nature, 1999, 399(6732): 151-155. DOI:10.1038/20187 (  0) 0) |
| [25] |
MILLER P, ZHABOTINSKY A M, LISMAN J E, et al. The stability of a stochastic CaMKⅡ switch: dependence on the number of enzyme molecules and protein turnover[J]. PLOS Biology, 2005, 3(4): 705-717. DOI:10.1371/journal.pbio.0030107 (  0) 0) |
| [26] |
ANTON O, FIRESTEIN B L. Lipids and phosphates at odds in synaptic depression[J]. Journal of Biological Chemistry, 2018, 293(5): 1568-1569. DOI:10.1074/jbc.H117.813808 (  0) 0) |
| [27] |
SONG S, MILLER K D, ABBOTT L F. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity[J]. Nature Neuroscience, 2000, 3(9): 919-926. DOI:10.1007/s00422-009-0332-7 (  0) 0) |
| [28] |
HEBB D O. The organization of behavior: A neuropsychological theory[M]. New York: Psychology Press, 1949: 119-120. DOI:10.1016/0013-4694(51)90070-3
(  0) 0) |
| [29] |
BIENENSTOCK E L, COOPER L N, MUNRO P W. Theory for the development of neuron selectivity: Orientation specificity and binocular interaction in visual cortex[J]. The Journal of Neuroscience, 1982, 2(1): 32-48. DOI:10.1142/9789812795885_0006 (  0) 0) |
 2022, Vol. 20
2022, Vol. 20


