蛋白质二级结构的预测始于20世纪60年代中期,早期主要根据PDB数据库的已知信息,运用统计方法计算单个残基或氨基酸序列片段形成某种二级结构的概率,来预测蛋白质二级结构类型[1]。近些年,随着计算机技术的进步,生物信息学为蛋白质二级结构的研究提供了有力的工具。蛋白质二级结构的研究主要聚焦于蛋白质结构与功能之间的关系,为研究、设计新药物提供理论参考[1],本文主要研究蛋白质序列与其二级结构类型的关系。
在研究过程中,学者们提出了各种基于序列特征的蛋白质结构分类和预测方法。Liu[2]等人提出Pse-in-One服务器,可以生成具有用户自己定义属性的特征向量,这些特征向量既可以体现蛋白质序列的特征,又很容易地与机器学习算法结合。Jo[3]等人探索了深度学习网络在蛋白质折叠识别中的应用,并验证了深度学习技术在折叠识别研究中的有效性。Yau[4]等人利用图示方法构造了蛋白质序列的矩向量。Yu[5]等人提出了K-string字典法,用来解决蛋白质序列比较中的高维向量问题。Dong[6]等人提出了mTM-align算法,为蛋白质多重结构比对提供可靠的支撑。Wei[7]等人开发了一种由综合特征集与集成分类器相结合而设计的蛋白质折叠预测方法PFPA。Khan[8]等人将关联规则挖掘技术ACO-AC应用于将蛋白质折叠分类。Wang[9]等人报道了一种基于人工智能的蛋白质结构优化方法AIR,将一维优化扩展到由多目标粒子群优化引擎驱动的三维空间优化。Yan[10]等人提出TSVM-fold和ESVM-fold两种算法,并证明TSVM-fold和ESVM-fold是蛋白质折叠识别的有效预测因子。
近几年,学者们在蛋白质结构预测和分类上收获得了更多成果。Zheng[11]等人开发了I-TASSER网关,实现了对蛋白质预测模型与已知模板的在线比对。Zheng[12]等人还开发了LOMETS2服务器,用于基于模板的蛋白质结构预测。Zhou[13]等人开发了DEMO,可方便地用于自动化基因组规模多结构域蛋白质的组装。Zhou[14]等人还提出了一种基于低估辅助的全局和局部协同差异进化(DE)的蛋白质三维结构预测方法。Zhang[15]等人提出了一种新的途径—MetaGO,可以在传统的序列同源性之外预测新的功能。Zhang[16]等人继续开发了新的开源方法—DeepMSA用于蛋白质二级结构的预测。Vangave[17]等人对基于模板和无模板方法的预测进行评估和整合,并提出了新的高置信度预测方法。Liu[18]等人提出了一种新的蛋白质折叠识别预测器:DeepSVM-fold。Liu[19]等人还采用学习排序模型(Learning to Rank model, LTR)对模板蛋白进行检索,提出了Fold-LTR-TCP预测器。Yan[20]等人提出了MV-fold和MT-fold两种算法。Li和Liu[21]提出了两种特征提取方法—MotifCNN和MotifDCNN以及一种预测器:MotifCNN-fold。
传统的蛋白质结构分类研究更多地关注蛋白质序列特征空间的划分,而本研究创新性地利用时间序列相关性方法来探索蛋白质序列特征之间的关系,并通过复杂网络建模来甄别不同结构类型对应蛋白质序列特征的异同。特别地,网络中心性结果具体地指出了不同蛋白质结构类型所对应的显著氨基酸和物理属性特征,这对深入研究蛋白质结构的分类与预测具有重要意义。
1 研究方法 1.1 蛋白质的序列特征 1.1.1 蛋白质序列的特征提取CATH数据库中的蛋白质结构主要分为三大类,即主要α结构类(Mainly α),主要β结构类(Mainly β)和α与β的混合结构类(Mixed α & β)。从CATH数据库中随机抽取24组序列,每种结构类型中分别获取8组;SCOP数据库包含四种结构类(All-α、All-β、α/β和α+β),从SCOP数据库的每种结构类中随机抽取5组蛋白质序列,总共获得20组蛋白质序列数据。我们利用自然向量(Natural vector, NV)、平均属性因子(Averaged property factors, APF)这两种经典的蛋白质序列特征提取方法从选取的蛋白质序列中提取特征向量。由于自然向量和平均属性因子特征向量分别为60维和10维,因此每个蛋白质序列对应一个70维的特征向量。
自然向量可以表示为一个60维的向量:〈nA, nR, …, nV, μA, μR, …, μV, D2A, D2R, …, D2V〉,该向量由三个部分组成,1-20维表示蛋白质序列中A,R,N,D,C,Q,E,G,H,I,L,K,M,F,P,S,T,W,Y,V这20种氨基酸的数量,用20个整数nA, nR, nN, …, nV表示;第21-40维元素为这20种氨基酸到原点总距离的平均值,记为
| $ \mu_k=\frac{T_k}{n_k}, k=A, R, N, \cdots, V $ | (1) |
其中
| $ D_j^k=\sum\limits_{i=1}^{n_k} \frac{\left(s[k][i]-\mu_k\right)^j}{n_k^{j-1} n^{j-1}}, j=1, 2, \ldots, n_k $ | (2) |
其中k表示20种氨基酸,n和nk分别为序列的长度和序列中氨基酸k的数目,k=A, R, N, ..., V。计算序列的自然向量时,规定若氨基酸k不存在,则nk, μk, Djk的值均为0[22]。Yu等证明了自然向量和蛋白质序列是一一对应的[22],该向量提取的是氨基酸的分布信息,而氨基酸物理属性可由平均属性因子来表示。Rakovsky提出了用一个10维向量来表示每条蛋白质序列的10种物理属性平均值[23]:
| $ X=\left(\left\langle f^{(1)}\right\rangle_S, \left\langle f^{(2)}\right\rangle_S, \cdots, \left\langle f^{(10)}\right\rangle_S\right) $ | (3) |
其中〈f(m)〉S为氨基酸序列S中第m种属性的平均值[23]:
| $ \left\langle f^{(m)}\right\rangle_S=\frac{1}{N_S} \sum\limits_{n=1}^{N_S} f_n^{(m)} $ | (4) |
NS表示氨基酸序列S的长度。这10种重要的氨基酸物理属性分别为:(1)α螺旋/弯曲偏好,(2)侧链大小,(3)扩展结构偏好,(4)疏水性,(5)双弯曲偏好,(6)氨基酸构成,(7)平面扩展偏好,(8)α区域出现的频率,(9)解离常数,(10)β结构的周围疏水性。这10种氨基酸物理属性的含义和取值由[24-25]给出。
通过计算自然向量(NV)和平均属性因子(APF),数据集中的每一条蛋白质序列都可以用一个70维的特征向量表示,在70维的向量空间中,每一个蛋白质可以看成70维实空间中的一个点。对于一个含有n个蛋白质的结构类,所有蛋白质的特征序列构成一个n×70维的特征序列矩阵,其中每一列代表一种特征因素,每一行为一个蛋白质序列的特征向量。
1.1.2 特征序列的随机排列由于特征序列长度即为该组数据蛋白质序列的个数,因此同一组数据的特征序列长度相等。为了减小蛋白质顺序对特征序列的影响,我们将所有特征序列的元素位置同时乱序,即将特征序列构成的特征序列矩阵的行进行随机乱序,随机乱序后仍保持特征序列同一位置对应相同蛋白质。我们通过计算平均标准差来衡量随机乱序后研究结果的鲁棒性。
1.2 特征序列之间的无向关系 1.2.1 互相关系数首先采用互相关系数来探索序列特征之间的关系。互相关系数是最基本的无向关系之一,它衡量了两个序列之间的线性相关性。对于一组特征序列{Xi, i=1, 2, ..., 70},序列Xi与Xj的互相关系数ρ(i, j)定义为[26]:
| $ \rho(i, j)=\frac{E\left[\left(X_i-E\left(X_i\right)\right)\left(X_j-E\left(X_j\right)\right)\right]}{\sqrt{{Var}\left(X_i\right) \cdot {Var}\left(X_j\right)}} $ | (5) |
其中E表示数学期望,Var表示方差。互相关系数取值介于[-1, 1]之间,为了计算特征序列之间无向关系,对互相关系数取绝对值, 得到R(i, j)=|ρ(i, j)|, i, j=1, 2, ..., 70。因此,对于每个数据集的70个特征序列,得到一个70×70维的互相关系数矩阵R=(R(i, j))70×70,该矩阵是对称的且矩阵元素R(i, j)取值介于[0, 1]之间,R(i, j)的值越接近1,说明序列之间的线性相关性越强,R(i, j)取值越低,说明序列之间的线性相关性越小。
1.2.2 标准化互信息互信息是信息理论中计算两个系统之间相互关系的量,它具有“无模型”的特点,即互信息计算的无向关系既可以是线性的也可以是非线性的,因此,互信息常用于现实世界中数据序列之间无向关系的计算。任给两个特征序列X和Y,可以计算Xi与Xj之间的互信息[27]:
| $ I\left(X_i ; X_j\right)=\sum p\left(x_i=\alpha, x_j=\beta\right) \log \frac{p\left(x_i=\alpha, x_j=\beta\right)}{p\left(x_i=\alpha\right) p\left(x_j=\beta\right)} $ | (6) |
其中α, β分别为序列Xi与Xj在同一位置的取值。为了实现节点间的相互比较,我们利用最大熵对标准化互信息进行归一化处理。特征序列Xi与Xj之间的标准化互信息定义为[27]:
| $ I^{\prime}\left(X_i ; X_j\right)=\frac{\max \left\{I\left(X_i ; X_j\right)\right\}}{\max\limits_{1 \leqslant q \leqslant 70} H_q} $ | (7) |
其中Hq为第q个特征序列的香浓熵。对于每个数据集的70个特征序列,我们得到一个70×70维的标准化互信息矩阵I′=(I′(Xi; Xj))70×70,该矩阵是对称的且矩阵元素介于0和1之间。
1.3 特征序列之间的有向关系互相关系数与标准化互信息计算的都是特征序列之间的无向关系,而传递熵则用来计算特征序列之间的有向信息传递。任意两个特征序列Xi与Xj之间的传递熵定义为[28]:
| $ T E_{X_j \rightarrow X_i}=\sum p\left(i_{n+1}, i_n^{(k)}, j_n^{(l)}\right) \log \frac{p\left(i_{n+1} \mid i_n^{(k)}, j_n^{(l)}\right)}{p\left(i_{n+1} \mid i_n^{(k)}\right)} $ | (8) |
其中in(k)=(in, ..., in-k+1)表示Xi的长度为k的时滞向量(嵌入向量),通常情况下取时间滞后l=k。
传递熵体现的是序列之间的有向信息传递,需要通过替代数据(Surrogate data)进行偏差校正。若令{in}和{jn}分别表示任意两个特征序列Xi与Xj,TEXj→Xi表示Xj到Xi的传递熵。首先将Xj固定,并对Xi的时间索引进行随机长度的时移,得到替代序列{in-τi},接下来,计算从Xj的原始序列{jn}到{in}的替代序列{in-τi}的传递熵,将结果记为TEXj→Xi(q),其中q是替代序列{in-τi}的指标,Xj→Xi的修正传递熵即为[29]:
| $ T E_{C, X_j \rightarrow X_i}=T E_{X_j \rightarrow X_i}-\max _q\left\{T E_{X_j \rightarrow X_i}(q)\right\} $ | (9) |
通过计算校正的传递熵,每一个结构类对应一个70×70维的传递熵矩阵TE=(TEC, Xj→Xi)70×70,该矩阵是非对称的且每个元素非负,矩阵中第(i, j)个元素TEC, Xj→Xi表示从序列Xj到Xi的传递熵。
1.4 蛋白质特征网络与中心性研究对CATH和SCOP数据库的每个主要结构类计算互相关系数、标准化互信息和传递熵矩阵,并将这些矩阵看作加权网络的邻接矩阵,以此建立以特征因素为节点的无向和有向加权网络。
1.4.1 网络与邻接矩阵在以节点和节点之间连接关系构成的网络中,通常用邻接矩阵来表示网络。在研究过程中,分别利用互相关系数、标准化互信息和传递熵来计算以特征因素为节点的网络邻接矩阵,进而利用中心性算法计算不同结构类型对应网络中特征因素的重要性分布。
1.4.2 无向网络的中心性为了探究网络之间的差异,首先需要探究网络节点的分布特征,而中心性方法则提供了衡量节点在网络中重要程度的方法。对于无向网络来说,中心性有一个最简单的计算方式,即度中心性[30]。在计算度中心性时,由于网络是无向的,因此邻接矩阵A是对称的,即A=AT,只需要计算每个节点所连接的边的总数。对于加权网络来说,度中心性即由邻接矩阵计算得到的加权边的权重之和。
另一个比较适用于无向网络中心性计算的方法是特征向量中心性[31]。特征向量中心性就是邻接矩阵的最大特征值对应的特征向量,即向量x满足:Ax=k1x,为了便于计算,上式也可以写为[32]
| $ x_i=k_1^{-1} \sum _j A_{i j} x_j $ | (10) |
其中k1为邻接矩阵A的最大特征值。
1.4.3 有向网络的中心性以上提到的度中心性和特征向量中心性比较适用于无向网络,在有向网络中,这两种中心性的计算方法存在一定的缺陷,需要进一步探究有向网络的中心性方法。有向网络的度中心性分为入度中心性和出度中心性,即每个节点的入边和出边数,在加权网络中分别体现为入边权重和出边权重的和。Katz在1953年提出了KATZ中心性[33],该中心性首先赋予网络中的每个节点一个很小的初始中心性,因为若一个节点只有从它出发的有向边而没有指向它的有向边,即只有出度没有入度,这些有向边给被它所指向的节点提供的中心性为零,这显然是不合理的。根据KATZ中心性的初始化思想,每个节点的中心性可以定义为[30]
| $ x_i=\alpha \sum _j A_{i j} x_j+\beta $ | (11) |
其中α和β是正常数,β是初始中心性。由于网络中心性计算的是网络中节点的重要性,因此中心性的具体数值并不重要,重要的是每个节点中心性的高低比较,给每个节点赋予一个较小的初始中心性并不会影响中心性的分布。上式可以写成矩阵形式[30]:
| $ x=\alpha A x+\beta \cdot 1 $ | (12) |
其中1是单位向量(1, 1, 1, ....),为了便于计算,β取值为1,则KATZ中心性为[30]
| $ x=(I-\alpha A)^{-1} \cdot 1 $ | (13) |
本文选取α=1/k1-0.001,根据x=(I-αA)-1·1计算有向网络的中心性。KATZ中心性存在一个缺陷,即当一个节点具有很高的KATZ中心性时,若它指向多个其它节点,这些节点也会有很高的KATZ中心性。PageRank[30]中心性则改进了这一点,PageRank中心性定义为[30]:
| $ x_i=\alpha \sum _j A_{i j} \frac{x_j}{k_j^{\text {out }}}+\beta $ | (14) |
当kjout=∑iAij=0时,第j个节点没有出边,
| $ x=\alpha A D^{-1} x+\beta \cdot 1 $ | (15) |
同样,取β=1,经过移项PageRank中心性还可以写成
| $ x=\left(I-\alpha A D^{-1}\right)^{-1} \cdot 1=D(D-\alpha A)^{-1} \cdot 1 $ | (16) |
从CATH和SCOP数据库的每个主要结构类中随机且尽可能等量地选取由X-ray实验获得、序列相似度不超过30%的PDB数据,其中从CATH的三个主要结构类中各随机选取8个CATH组(按CATH ID分类的组),并从SCOP数据库的四个主要结构类中各随机选取5个SCOP组,数据选取的结果(见表 1)。这两个数据库的不同结构类数据集之间无冗余序列。由于两个数据库对子类划分方式不同,在尽量避免冗余的情况下,α、β、α与β的混合结构类每一种类型的不同数据库数据集之间仍然存在一定交集,平均冗余度为7.5%,不影响实验结果。
| 表 1 CATH和SCOP结构分类数据库数据选取 Table 1 Data selected from CATH and SCOP |
分别采用互相关系数、标准化互信息和传递熵的方法对序列特征之间的无向和有向关系进行计算。由于不同类型的序列特征取值分布不同,将60维的自然向量按其组成部分分为N特征(1-20维,表示20种氨基酸在蛋白质序列中的个数),μ特征(21-40维,表示20种氨基酸在蛋白质序列中距首个氨基酸的平均距离)和D特征(41-60维,表示20种氨基酸在蛋白质序列中距首个氨基酸距离的二阶归一化中心矩),并分别对N、μ、D特征以及10维的平均属性因子(氨基酸的10种物理属性)特征计算无向和有向的关系矩阵,并将计算结果用彩图的方式展现(见图 1~图 4和图 5~图 8)。分别展示了CATH和SCOP两组数据集在每种序列特征下的关系矩阵。
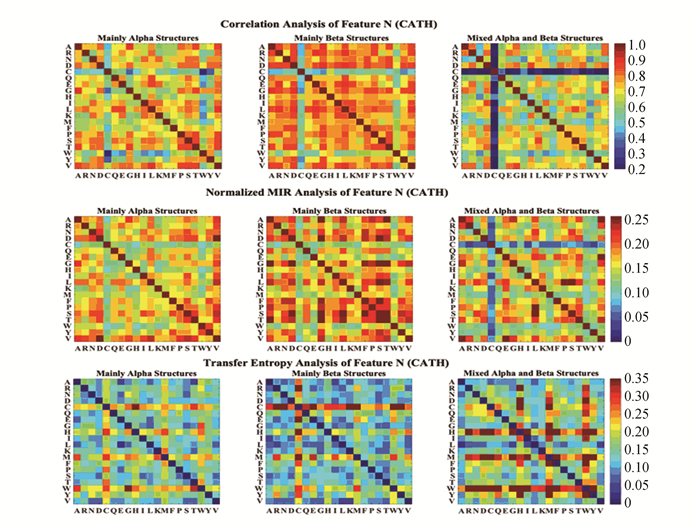
|
图 1 特征N的相关性分析(CATH) Figure 1 Analysis of feature N (CATH) 注:图片由上至下分别表示基于互相关系数、标准化互信息和传递熵矩阵计算的CATH数据库中三种蛋白质结构类的20种氨基酸N特征(氨基酸数量)之间的关系,其中基于互相关系数矩阵和标准化互信息的计算结果为对称矩阵。 |
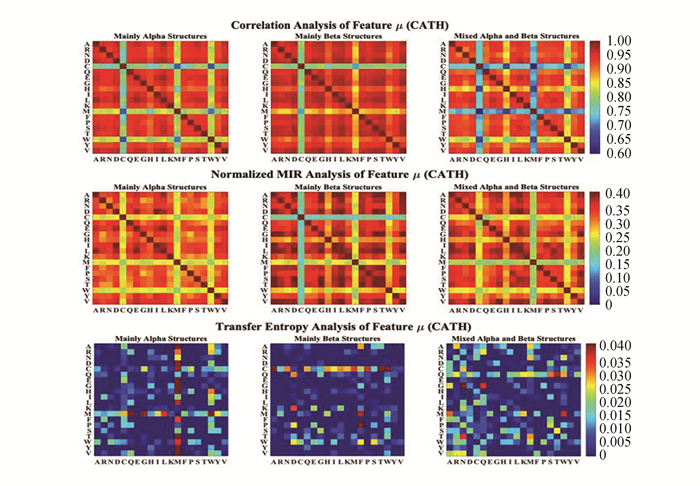
|
图 2 特征μ的相关性分析(CATH) Figure 2 Analysis of feature μ(CATH) 注:CATH数据库中三种蛋白质结构类的20种氨基酸μ特征(每种氨基酸到序列首个氨基酸距离平均值)之间的关系. |
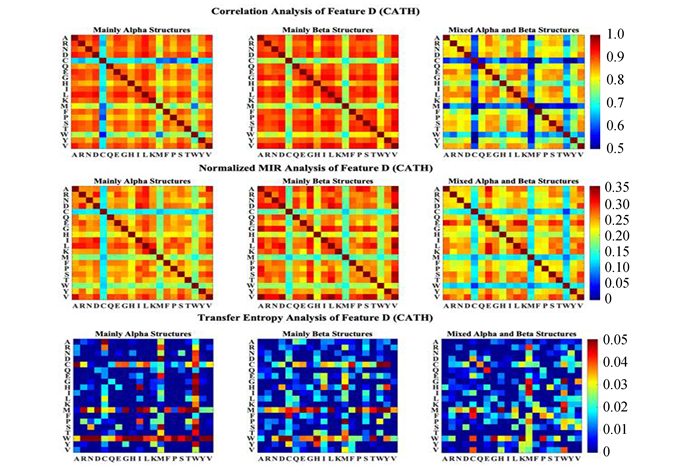
|
图 3 特征D的相关性分析(CATH) Figure 3 Analysis of feature D (CATH) 注:CATH数据库三种蛋白质结构类的20种氨基酸D特征(归一化中心矩)之间的关系. |
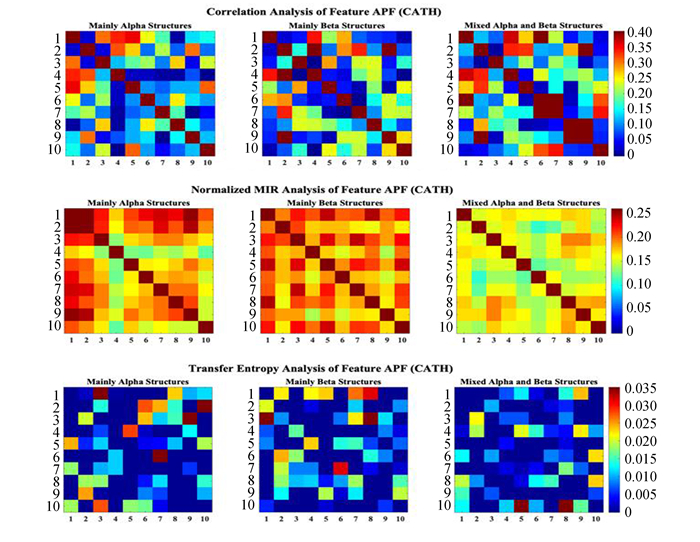
|
图 4 特征APF的相关性分析(CATH) Figure 4 Analysis of feature APF (CATH) 注:CATH数据库三种蛋白质结构类APF特征(氨基酸的10种物理属性)之间的关系. |
|
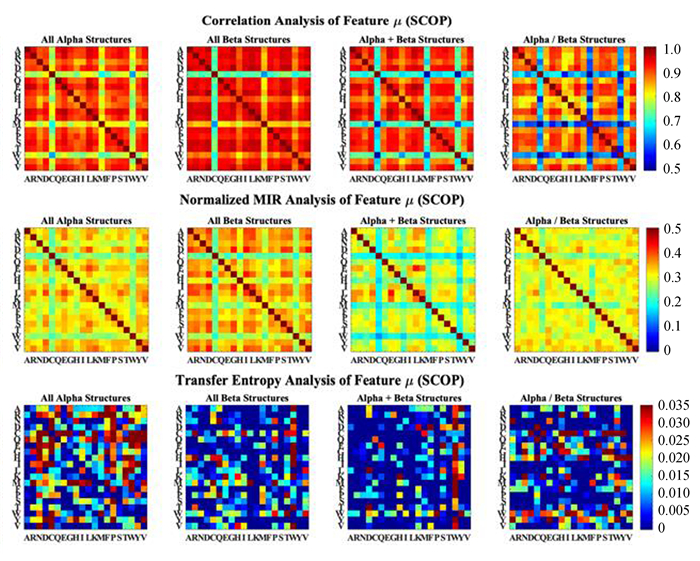
图 5 特征N的相关性分析(SCOP) Figure 5 Analysis of feature N (SCOP) 注:SCOP数据库四种蛋白质结构类的20种氨基酸N特征(氨基酸数量)之间的关系. |
|
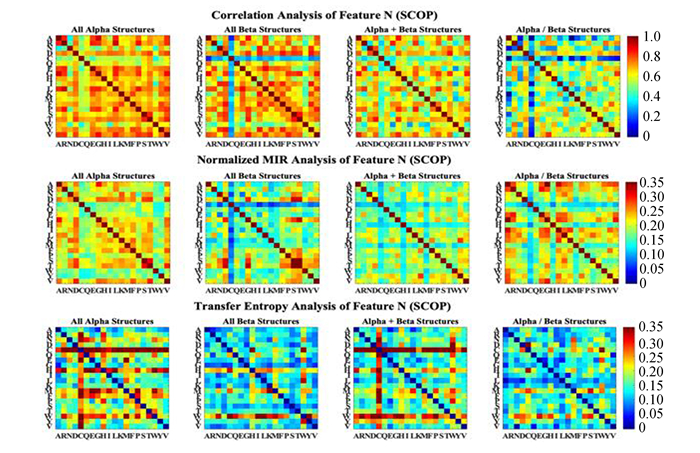
图 6 特征μ的相关性分析(SCOP) Figure 6 Analysis of featureμ(SCOP) 注:SCOP数据库四种蛋白质结构类的20种氨基酸μ特征(每种氨基酸到序列首个氨基酸距离的平均值)之间的关系. |
|
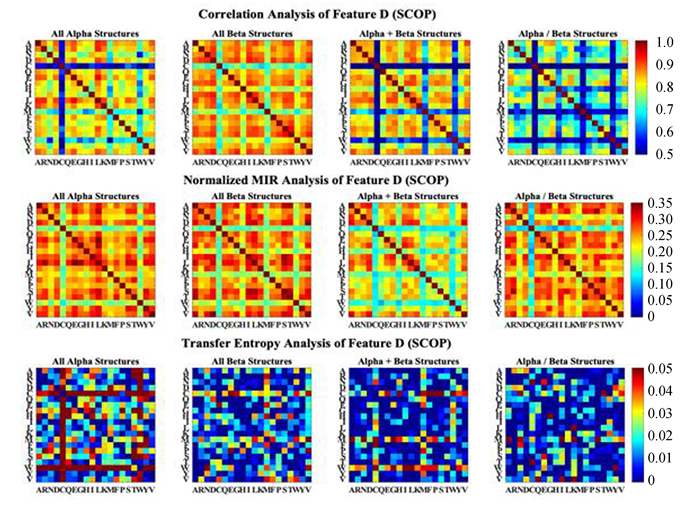
图 7 特征D的相关性分析(SCOP) Figure 7 Analysis of feature D (SCOP) 注:SCOP数据库四种蛋白质结构类的20种氨基酸D特征(归一化中心矩)之间的关系. |
|
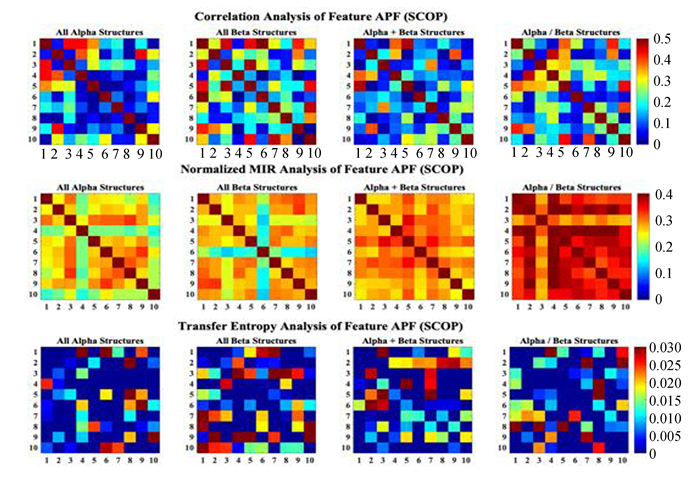
图 8 特征APF的相关性分析(SCOP) Figure 8 Analysis of feature APF (SCOP) 注:SCOP数据库四种蛋白质结构类APF特征(氨基酸的10种物理属性)之间的关系. |
从这些彩色矩阵中可以明显看出某些氨基酸或物理属性的序列特征与其它同类型特征之间具有较强或较弱的关系。利用这些无向和有向的关系矩阵构建以序列特征为节点的加权网络,并利用网络中心性算法来分析不同结构类型下蛋白质序列特征因素的重要性分布。
2.3 不同结构类型序列特征网络中心性分析利用对称的互相关系数矩阵和标准化互信息矩阵构建无向的加权网络,并利用非对称的传递熵矩阵构建有向的加权网络。由于网络中心性衡量的是网络中节点的重要程度,同一个网络中不同节点之间中心性的高低比中心性的具体数值更重要。为了便于观察分析,将同一个关系矩阵构建的网络中各个节点的中心性结果进行标准化,将中心性的取值按照x=x/maxx调整至[0, 1]区间内,其中x为中心性向量,maxx为中心性向量x中的最大分量值。
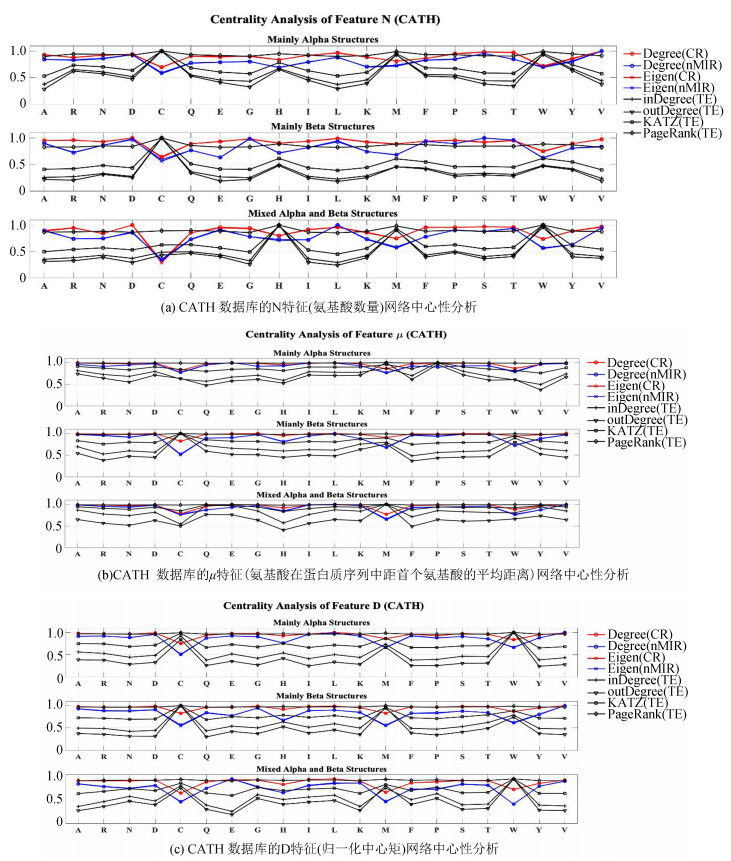
CATH数据集得到的N、μ、D特征网络中心性结果见图 9。从图 9中可以看出,三种结构类均在半胱氨酸(C)、甲硫氨酸(M)、色氨酸(W)的三种特征上体现出较低的无向网络中心性(度中心性和特征向量中心性)与较高的有向网络中心性(KATZ和PageRank中心性),而在色氨酸(A)、天冬氨酸(D)、亮氨酸(L)、缬氨酸(V)的三种特征上体现出较强的无向网络中心性和较弱的有向网络中心性。这表明半胱氨酸(C)、甲硫氨酸(M)和色氨酸(W)的构成和排序与其它氨基酸的构成和排序之间对称关系较弱而非对称关系较强,而色氨酸(A)、天冬氨酸(D)、亮氨酸(L)、缬氨酸(V)与其它氨基酸的构成与排序之间对称关系较强而非对称关系较弱,组氨酸(H)的N特征也体现出较强的有向网络中心性,表明组氨酸(H)的个数与其它氨基酸的个数之间也具有较强的非对称关系。Mainly α结构类在脯氨酸(P)的排序(μ特征)上体现出较强的有向网络中心性,而Mainly β结构类在甘氨酸(G)的构成和排序上具有较强的无向网络中心性;Mixed α & β的混合结构类在组氨酸(H)的N特征上明显体现出偏高的有向网络中心性。
|
图 9 CATH数据库的N、μ、D特征网络中心性分析 Figure 9 Centrality analysis of feature N, μ, D (CATH) 注:图中X轴表示20种氨基酸,Y轴表示标准化的中心性结果,Degree(CR)、Degree(nMIR)和Eigen(CR)、Eigen(nMIR)分别表示由两种对称关系得到的度中心性与特征向量中心性;inDegree(TE)、outDegree(TE)、KATZ(TE)和PageRank(TE)分别表示传递熵对应的中心性. |
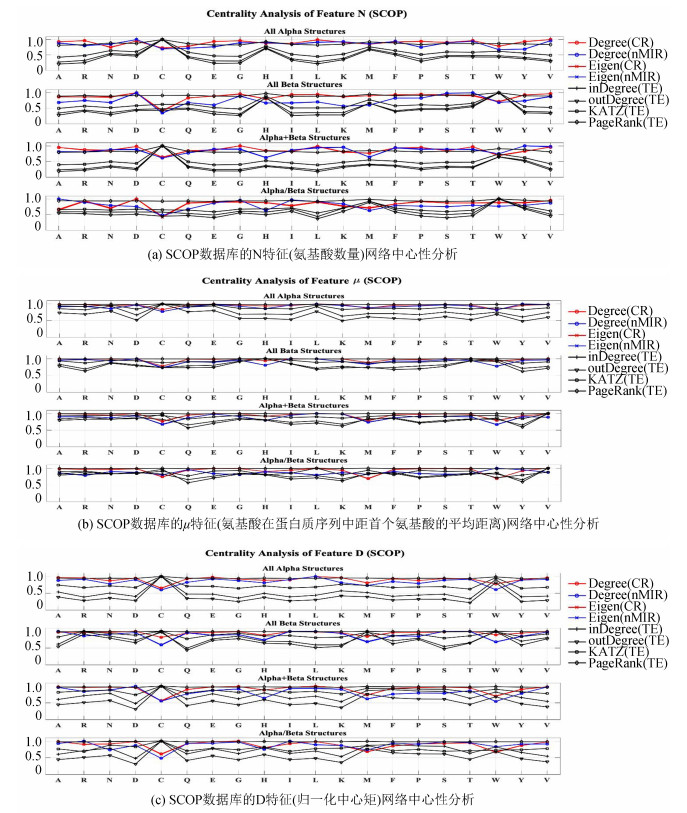
SCOP数据库得到的N、μ、D特征中心性结果见图 10。可以看出SCOP的四种结构类在半胱氨酸(C)与色氨酸(W)的构成和排序以及组氨酸(H)、甲硫氨酸(M)的排序特征具有较低的无向网络中心性和较高的有向网络中心性。这表明这些氨基酸与其它氨基酸的特征之间具有较弱的对称关系与较强的非对称关系,而色氨酸(A)、天冬氨酸(D)、亮氨酸(L)和缬氨酸(V)对应较强的无向网络中心性和较弱的有向网络中心性,表明这些氨基酸与其它氨基酸的构成和排序之间具有较强的对称关系与较弱的非对称关系。这些特点是SCOP的四种结构类的共性,这也可以从图 5-图 7中看出。
|
图 10 SCOP数据库的N、μ、D特征网络中心性分析 Figure 10 Centrality analysis of feature N, μ, D (SCOP) 注:图中X轴表示20种氨基酸,Y轴表示标准化的中心性结果,Degree(CR)、Degree(nMIR)和Eigen(CR)、Eigen(nMIR)分别表示由两种对称关系得到的度中心性与特征向量中心性;inDegree(TE)、outDegree(TE)、KATZ(TE)和PageRank(TE)分别表示传递熵对应的中心性. |
All-α结构类天冬酰胺(N)的构成和排序特征具有较高的有向网络中心性,这表明天冬酰胺(N)与其它氨基酸的特征之间具有较强的非对称关系。All-β结构类中苏氨酸(T)的排序特征的无向和有向网络中心性均较高,这是与All-α结构类的最明显的差别,All-α结构类的苏氨酸(T)的排序特征有向网络中心性较低,低于丝氨酸(S)排序特征的有向网络中心性,而All-β结构类中苏氨酸(T)的排序特征在有向网络中心性上明显高于丝氨酸(S),这与CATH数据集的结果具有一定相似性。此外,在All-β结构类中甘氨酸(G)的排序特征的无向和有向网络中心均较强,而All-α结构类在甘氨酸(G)的排序特征上具有较弱的有向网络中心性,这表明在All-β结构类中甘氨酸(G)的排序特征与其它氨基酸的排序特征之间具有较强的对称和非对称关系,而在All-α结构类中甘氨酸(G)的排序与其它氨基酸的排序之间有向关系较弱。α/β与α+β结构类分别继承了All-α与All-β结构类的一些特点。
从图 9-图 10中可以看出,半胱氨酸(C)、色氨酸(W)、甲硫氨酸(M)的有向网络中心性偏高,而无向网络中心性偏低。导致这种中心性差异的原因可能是由于这些氨基酸与其它氨基酸之间具有较强的相互作用(有向网络中心性高),这些相互作用之间关系复杂,具有不确定性,而无向网络中心性低则说明尽管特征之间有紧密的相互作用,但不同氨基酸的特征之间并不能彼此相互决定。这种中心性差异是不同结构类的共有特征,这种共有的强烈而复杂的相互作用,可能由氨基酸的物理化学性质,例如:亲水性、侧链基团的极性,以及这些氨基酸的功能和作用所导致,而这种氨基酸之间的强烈相互作用可能与结构类型的选择无关。
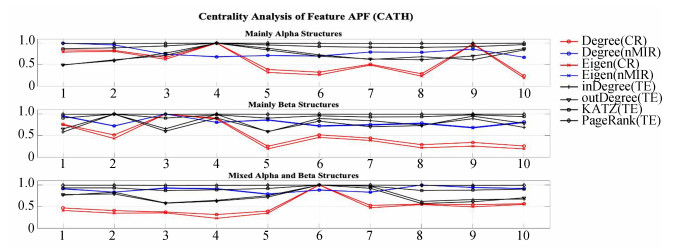
CATH和SCOP数据集的APF特征中心性结果见图 11-图 12。在CATH数据结果中,Mainly α结构类的氨基酸α螺旋/弯曲偏好(1)、侧链的大小(2)、解离常数(9)无向网络中心性较高,对称关系较强,氨基酸疏水性(4)的线性无向网络(即线性CR关系建立的网络)和有向网络中心性高,而非线性无向网络(即非线性nMIR关系建立的网络)中心性较低,氨基酸扩展结构偏好(3)、双弯曲偏好(5)、氨基酸组成(6)、α区域出现的频率(8)、β结构的周围疏水性(10)的线性无向网络中心性较低,表明这些物理属性与其它属性之间的线性对称关系较弱。Mainly β结构的氨基酸α螺旋/弯曲偏好(1)、氨基酸扩展结构偏好(3)无向网络中心性高,氨基酸疏水性(4)的无向和有向网络中心性均较高,表明对称和非对称关系均较高,侧链的大小(2)的无向网络中心性较低,与其它属性的对称关系较弱,双弯曲偏好(5)、α区域出现的频率(8)、β结构的周围疏水性(10)的线性无向网络中心性较低,表明这些属性与其它属性的线性对称关系较弱。Mixed α&β结构类的氨基酸组成(6)的无向和有向网络中心性均较高,与其它属性的对称和非对称关系均较强,氨基酸α螺旋/弯曲偏好(1)、氨基酸扩展结构偏好(3)、氨基酸疏水性(4)的线性无向网络中心性偏低,而非线性无向网络中心性偏高,表明这些属性具有较强的非线性对称关系。
|
图 11 CATH数据库的APF特征网络中心性分析 Figure 11 Centrality analysis of feature APF (CATH) 注:上图为CATH数据库特征APF(平均属性因子)的网络中心性计算结果。图中数字代表十种平均属性因子. |
|
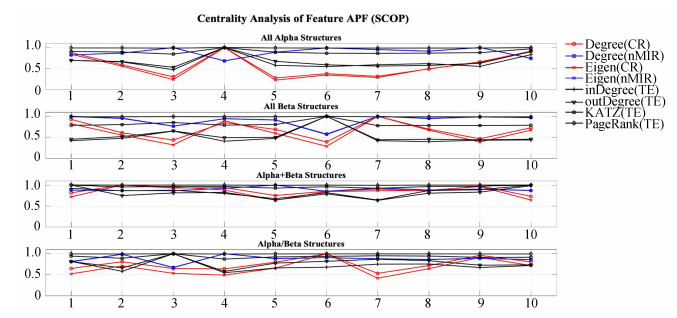
图 12 SCOP数据库的APF特征网络中心性分析 Figure 12 Centrality analysis of feature APF (SCOP) 注:上图为SCOP数据库特征APF(平均属性因子)的网络中心性计算结果。图中数字代表十种平均属性因子. |
类似地,在SCOP的结果中,All-α结构类α螺旋/弯曲偏好(1)、疏水性(4)、β结构的周围疏水性(10)的线性无向网络与有向网络中心性均较高,而扩展结构偏好(3)、双弯曲偏好(5)、氨基酸构成(6)、平面扩展偏好(7)的线性无向网络中心性偏低,而非线性无向网络中心性偏高。All-β结构类中(1)、疏水性(4)、平面扩展偏好(7)、β结构的周围疏水性(10)的无向网络中心性偏高,而有向网络中心性偏低,扩展结构偏好(3)、氨基酸构成(6)的无向网络中心性偏低,而有向网络中心性偏高,(9)的线性无向网络中心性偏低。在α+β结构中,α螺旋/弯曲偏好(1)、β结构的周围疏水性(10)的线性无向网络中心性偏低,(5)的线性无向网络中心性偏低,而非线性无向网络中心性偏高,侧链大小(2)、扩展结构偏好(3)、疏水性(4)、平面扩展偏好(7)、解离常数(9)的无向网络中心性偏高。α/β结构中,α螺旋/弯曲偏好(1)、扩展结构偏好(3)的无向网络中心性偏低,而有向网络中心性偏高,侧链大小(2)、氨基酸构成(6)、解离常数(9)的无向网络中心性偏高。
经过上述分析发现α结构类的α螺旋/弯曲偏好(1)与其它属性的对称关系较强,疏水性(4)的线性对称和非对称关系较强,非线性关系较弱,而扩展结构偏好(3)、双弯曲偏好(5)、氨基酸构成(6)的线性对称关系较弱。β结构类的α螺旋/弯曲偏好(1)、疏水性(4)对称关系较强,而氨基酸构成(6)的非对称关系较强。混合结构类中氨基酸构成(6)的对称和非对称关系均较强,α螺旋/弯曲偏好(1)的线性对称关系较弱。
3 讨论通过计算蛋白质序列特征之间的无向和有向关系,建立蛋白质特征加权网络,并利用网络中心性算法来探索不同蛋白质结构类型的差异。不同于以往的蛋白质结构研究,网络中心性的结果可以推断出具体的氨基酸特征和物理属性对不同蛋白质结构类型的影响,研究结果对蛋白质二级结构的分类和预测研究具有参考和指导意义。
通过提取蛋白质序列的氨基构成和排序,以及重要物理属性,每个蛋白质序列对应一个70维特征向量,该向量前60维为自然向量特征,而61-70维为氨基酸的10种重要物理属性平均值。为了减小蛋白质顺序对特征序列之间关系的影响,我们对蛋白质特征序列进行随机乱序处理,而网络中心性结果的平均标准差验证了随机乱序后结果的鲁棒性。在三种关系矩阵计算方法中,互相关系数和标准化互信息分别衡量了序列特征之间的线性和非线性关系,两者均为对称关系,而传递熵则度量了特征序列之间的有向信息传递。互相关系数和标准化互信息所描述的对称关系,可以看成一种确定性的对称关系,例如,一个序列X与它自身的互相关系数和标准化互信息均为1,表明X与它自己之间具有很强的确定性的对称关系;而X与它自身之间的传递熵为0,也验证了X与它自身之间的确定性关系。而在线性回归模型中,若一个序列X的线性回归方程中含有另一个序列Y的时滞向量,则从Y到X的传递熵为正,而互相关系数和标准化互信息均为0,这表明Y到X之间具有有向的信息传递,而由于回归方程中误差项的存在,导致Y对X的影响具有非确定性[32-33]。因此,互相关系数、标准化互信息和传递熵这三种方法的取值之间是相互独立的。
在网络中心性计算中,中心性度量网络节点的重要性,其具体数值并不重要,重要的是同一网络中不同节点的中心性之间的高低比较。在无向网络中,节点的中心性高表明该节点所代表的特征与同一网络中其它特征之间的对称关系较强;而在有向网络中,节点的中心性高则表明该特征与同一网络的其它特征之间非对称关系较强。
通过分析70维融合特征向量,我们发现不同蛋白质结构类型的共性主要体现在自然向量特征上,其中不带电荷的极性半胱氨酸(C)、非极性色氨酸(W)、带正电荷组氨酸(H)、非极性甲硫氨酸(M)的构成和排序与其它氨基酸的特征之间具有较弱的对称和较强的非对称关系(即不确定性复杂相互作用),而非极性色氨酸(A)、带负电荷的天冬氨酸(D)、非极性亮氨酸(L)和非极性缬氨酸(V)的构成和排序与其它氨基酸的特征之间具有较强的对称关系和较弱的非对称关系,这是CATH和SCOP的所有主要结构类的共同特征,与不同结构的选择无关。从氨基酸极性角度观察,α结构类的特征主要体现在非极性脯氨酸(P)和极性天冬酰胺(N)上,而β结构类的特征主要体现在不带电的极性氨基酸上,例如苏氨酸(T)和甘氨酸(G),其中α与β结构的差异则体现在丝氨酸(S)、苏氨酸(T)、甘氨酸(G)等氨基酸与其它氨基酸特征之间关系的强弱,以及氨基酸物理属性之间关系的强弱上。从70维融合特征向量的中心性分布中可以看出,氨基酸的物理属性中心性对不同蛋白质结构类型的分布差异较大,而氨基酸的构成和排序特征中心性对不同结构类型的分布存在一定差异但幅度较小。我们可以推断氨基酸的物理属性对区分不同结构类型影响较大。
分析了不同结构类对应的重要氨基酸和物理属性特征,总结了不同蛋白质结构类在序列特征关系上的异同。通过考虑不同结构类型的序列特征差异,有助于开发新的蛋白质结构分类和预测算法,本研究所使用的复杂网络方法还可用于进化分类或更深层次结构分类的研究,对蛋白质结构的研究和发展具有重要意义。
4 结论通过对不同结构类型的蛋白质序列特征进行网络建模,发现了不同结构类型对应序列特征之间的关系的共性和差异。研究发现,CATH和SCOP的主要结构类型均在半胱氨酸(C)、色氨酸(W)、组氨酸(H)和甲硫氨酸(M)的构成和排序上具有较弱的对称和较强的非对称关系,而在丙氨酸(A)、天冬氨酸(D)、亮氨酸(L)和缬氨酸(V)的构成和排序上具有较强的对称和较弱的非对称关系,这种共性可能与蛋白质结构类型的选择无关;而α与β结构的差异则体现在丝氨酸(S)、苏氨酸(T)、甘氨酸(G)以及氨基酸物理属性等特征关系的强弱上。
| [1] |
王举, 王兆月, 田心, 等. 生物信息学: 基础及应用[M]. 北京: 清华大学出版社, 2014. WANG Ju, WANG Zhaoyue, TIAN Xin, et al. Bioinformatics: Fundamentals and applications[M]. Beijing: Tsinghua University Press, 2014. (  0) 0) |
| [2] |
LIU B, LIU F, WANG X, et al. Pse-in-One: A web server for generating various modes of pseudo components of DNA, RNA, and protein sequences[J]. Nucleic Acids Research, 2015, 43(1): W65-W71. DOI:10.1093/nar/gkv458 (  0) 0) |
| [3] |
JO T, HOU J, EICKHOLT J, et al. Improving protein fold recognition by deep learning networks[J]. Scientific Reports, 2015, 5: 17573. DOI:10.1038/srep17573 (  0) 0) |
| [4] |
YAU S S T, YU C, HE R. A protein map and its application[J]. DNA and Cell Biology, 2008, 27(5): 241-250. DOI:10.1089/dna.2007.0676 (  0) 0) |
| [5] |
YU C, HE R, YAU S S T. Protein sequence comparison based on K-string dictionary[J]. Gene, 2013, 529(2): 250-256. DOI:10.1016/j.gene.2013.07.092 (  0) 0) |
| [6] |
DONG R, PENG Z, ZHANG Y, et al. mTM-align: An algorithm for fast and accurate multiple protein structure alignment[J]. Bioinformatics, 2018, 34(10): 1719-1725. DOI:10.1093/bioinformatics/btx828 (  0) 0) |
| [7] |
WEI L, LIAO M, GAO X, et al. Enhanced protein fold prediction method through a novel feature extraction technique[J]. IEEE Transactions on Nanobioscience, 2015, 14(6): 649-659. DOI:10.1109/TNB.2015.2450233 (  0) 0) |
| [8] |
KHAN M A, SHAHZAD W, BAIG A R. Protein classification via an ant-inspired association rules-based classifier[J]. International Journal of Bio-Inspired Computation, 2016, 8(1): 51. DOI:10.1504/IJBIC.2016.074631 (  0) 0) |
| [9] |
WANG D, GENG L, ZHAO Y J, et al. Artificial intelligence-based multi-objective optimization protocol for protein structure refinement[J]. Bioinformatics, 2020, 36(2): 437-448. DOI:10.1093/bioinformatics/btz544 (  0) 0) |
| [10] |
YAN K, WEN J, LIU J X, et al. Protein fold recognition by combining support vector machines and pairwise sequence similarity scores[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2020, 18(5): 2008-2016. DOI:10.1109/TCBB.2020.2966450 (  0) 0) |
| [11] |
ZHENG W, ZHANG C, BELL E W, et al. I-TASSER gateway: A protein structure and function prediction server powered by XSEDE[J]. Future Generation Computer Systems, 2019, 99: 73-85. DOI:10.1016/j.future.2019.04.011 (  0) 0) |
| [12] |
ZHENG W, ZHANG C, WUYUN Q, et al. LOMETS2: Improved meta-threading server for fold-recognition and structure-based function annotation for distant-homology proteins[J]. Nucleic Acids Research, 2019, 47(W1): W429-W436. DOI:10.1093/nar/gkz384 (  0) 0) |
| [13] |
ZHOU X, HU J, ZHANG C, et al. Assembling multidomain protein structures through analogous global structural alignments[J]. Proceedings of the National Academy of Sciences, 2019, 116(32): 15930-15938. DOI:10.1073/pnas.1905068116 (  0) 0) |
| [14] |
ZHOU X G, PENG C X, LIU J, et al. Underestimation-assisted global-local cooperative differential evolution and the application to protein structure prediction[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(3): 536-550. DOI:10.1109/TEVC.2019.2938531 (  0) 0) |
| [15] |
ZHANG C, ZHENG W, FREDDOLINO P L, et al. MetaGO: Predicting gene ontology of non-homologous proteins through low-resolution protein structure prediction and protein-protein network mapping[J]. Journal of Molecular Biology, 2018, 430(15): 2256-2265. DOI:10.1016/j.jmb.2018.03.004 (  0) 0) |
| [16] |
ZHANG C, ZHENG W, MORTUZA S M, et al. DeepMSA: Constructing deep multiple sequence alignment to improve contact prediction and fold-recognition for distant-homology proteins[J]. Bioinformatics, 2020, 36(7): 2105-2112. DOI:10.1093/bioinformatics/btz863 (  0) 0) |
| [17] |
VANGAVETI S, VREVEN T, ZHANG Y, et al. Integrating ab initio and template-based algorithms for protein-protein complex structure prediction[J]. Bioinformatics, 2020, 36(3): 751-757. DOI:10.1093/bioinformatics/btz623 (  0) 0) |
| [18] |
LIU B, LI C C, YAN K. DeepSVM-fold: Protein fold recognition by combining support vector machines and pairwise sequence similarity scores generated by deep learning networks[J]. Briefings in Bioinformatics, 2019, 21(5): 1733-1741. DOI:10.1093/bib/bbz098 (  0) 0) |
| [19] |
LIU B, ZHU Y, YAN K. Fold-LTR-TCP: Protein fold recognition based on triadic closure principle[J]. Briefings in bioinformatics, 2019, 21(6): 2185-2193. DOI:10.1093/bib/bbz139 (  0) 0) |
| [20] |
YAN K, FANG X, XU Y, et al. Protein fold recognition based on multi-view modeling[J]. Bioinformatics, 2019, 35(17): 2982-2990. DOI:10.1093/bioinformatics/btz040 (  0) 0) |
| [21] |
LI C C, LIU B. MotifCNN-fold: Protein fold recognition based on fold-specific features extracted by motif-based convolutional neural networks[J]. Briefings in Bioinformatics, 2020, 21(6): 2133-2141. DOI:10.1093/bib/bbz133 (  0) 0) |
| [22] |
YU C, DENG M, CHENG S Y, et al. Protein space: A natural method for realizing the nature of protein universe[J]. Journal of Theoretical Biology, 2013, 318: 197-204. DOI:10.1016/j.jtbi.2012.11.005 (  0) 0) |
| [23] |
RACKOVSKY S. Sequence physical properties encode the global organization of protein structure space[J]. Proceedings of the National Academy of Sciences of the United States of America, 2009, 106(34): 14345-14348. DOI:10.1073/pnas.0903433106 (  0) 0) |
| [24] |
KIDERA A, KONISHI Y, OKA M, et al. Statistical analysis of the physical properties of the 20 naturally occurring amino acids[J]. Journal of Protein Chemistry, 1985, 4(1): 23-55. DOI:10.1007/BF01025492 (  0) 0) |
| [25] |
KIDERA A, KONISHI Y, OOI T, et al. Relation between sequence similarity and structural similarity in proteins. role of important properties of amino acids[J]. Journal of Protein Chemistry, 1985, 4(5): 265-297. DOI:10.1007/BF01025494 (  0) 0) |
| [26] |
王燕. 应用时间序列分析[M]. 北京: 中国人民大学, 2008. WANG Yan. Applied Time Series Analysis[M]. Beijing: Renmin University of China, 2008. (  0) 0) |
| [27] |
WAN X, ZHAO X, YAU S S T. An information-based network approach for protein classification[J]. PloS One, 2017, 12(3): e0174386. DOI:10.1371/journal.pone.0174386 (  0) 0) |
| [28] |
SCHREIBER T. Measuring information transfer[J]. Physical Review Letters, 2000, 85(2): 461-464. DOI:10.1103/PhysRevLett.85.461 (  0) 0) |
| [29] |
LUNGARELLA M, PITTI A, KUNIYOSHI Y. Information transfer at multiple scales[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2007, 76(5): 056117. DOI:10.1103/PhysRevE.76.056117 (  0) 0) |
| [30] |
NEWMAN M E J. Networks-An introduction[M]. Oxford: Oxford University Press, Inc., 2010: 99-106, 167-179. DOI:10.1093/acprof:oso/9780199206650.001.0001
(  0) 0) |
| [31] |
COVER T M, THOMAS J A, WILEY J. Elements of Information Theory[M]. Beijing: Tsinghua University Press, 2003.
(  0) 0) |
| [32] |
VEJMELKA M, PALUS M. Inferring the directionality of coupling with conditional mutual information[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2008, 77(2): 02614. DOI:10.1103/PhysRevE.77.026214 (  0) 0) |
| [33] |
HLAVAKOVA-SSCHNDLER K, PALU M, VEJMELKA M, et al. Causality detection based on information-theoretic approaches in time series analysis[J]. Physics Reports, 2007, 441(1): 1-46. DOI:10.1016/j.physrep.2006.12.004 (  0) 0) |
 2022, Vol. 20
2022, Vol. 20


