2. 包头医学院 基础与法医学院, 内蒙古 包头 014000;
3. 呼和浩特第一医院, 呼和浩特 010051
2. School of Medical School of Foundation, Baotou Medical College, Baotou 014000, Inner Mongolia, China;
3. Hohhot First Hospital, Hohhot 010051, China
蛋白质通过与配体的相互作用来执行生物学功能[1-3],所以准确地识别蛋白质结合残基与配体结合位点是理解蛋白质生物学功能,药物设计和疾病治疗的关键。血红素HEME辅因子是一种极其通用的辅基,对几乎所有的生物执行功能都至关重要[4-7]。例如亚铁血红素辅因子通常与血红素蛋白结合,在多种生物过程中发挥重要作用,包括电子转移、氧气转运、金属离子储存、化学催化、基因表达、细胞信号转导等[8-10]。所以对血红素结合位点残基的识别有助于更好地理解血红素结合蛋白的生物学功能,揭示血红素-蛋白相互作用的机制,为生物启发蛋白设计提供有价值的线索[11]。然而, 实验测定血红素结合残基既费时又费力还耗材,因此,很有必要开发能够预测血红素结合残基的计算方法。
国内外很多学者对蛋白质与配体结合位点进行了研究。如2008年,Jessica等人[12]对Zn2+配体的结合位点进行预测;Babor等人基于3D结构开发了CHED算法,预测了Zn2+, Co2+, Ni2+, Fe2+, Cu2+, Mn2+金属的结合位点[13-14], 2019年Zhu等人利用机器学习方法预测了多种蛋白质配体等[15]。2013年,Zhang等人[16]收集了配体和蛋白质之间相互作用,整理得到Biolip数据库,这是一个半手工蛋白质离子配体数据库,比较全面地注释了蛋白质配体及其结合残基信息。Biolip数据库中每个条目都包含了对以下内容的注释:配体结合残基、配体结合亲和力、催化位点、委员会编号、基因本体术语和其他数据库的交叉链接等。数据库中包含了极其广泛和精准的配体蛋白数据,之后很多学者使用Biolip数据库中的配体信息来预测蛋白质配体结合位点。如2016年,Hu等人[17]使用SVM方法较好地识别了Biolip数据库中Cu2+, Fe2+, Fe3+等金属离子配体的结合位点;2017年Gao等人[18]统计分析了金属配体结合残基序列片段的信息,使用SVM算法对Biolip数据库中Zn2+, Co2+, Ni2+, Fe2+, Cu2+, Mn2+等金属离子配体的结合位点进行预测等等。
2011年,Liu等人[19]等人使用支持向量机的方法,考虑血红素配体结合残基及其附近残基的溶剂可及性面积、进化保守性、深度和突出性等特征,对含有血红素配体的141条无冗的蛋白结合位点进行了预测,得到总精度76.49%和MCC为0.407。Liu等人[20]也利用支持向量机方法,对同样的蛋白序列,通过结合序列的拓扑特征和结构特征来识别血红素结合残基,得到总精度85.99%和MCC为0.489。2019年,Zhao等人[21]使用SXGBsite方法对Biolip数据库中27条含血红素蛋白质进行预测,得到总精度96.2%和MCC为0.618。
本文从Biolip数据库中下载了蛋白质和血红素结合的相关数据,并且进行了整理,然后从中提取了有益信息,使用Fisher判别法和矩阵打分方法进行了计算,得到了较好的预测结果,并与前人进行了比较,为HEME与蛋白质结合提供有益信息。
1 数据及方法 1.1 数据集从Biolip数据库下载整理了已知血红素与蛋白质结合信息, 得到蛋白链2 952条,筛选分辨率好于3Å、序列长度大于50个残基,序列相似性低于40%的蛋白质链254条。由于蛋白质序列中,残基和血红素配体结合不仅仅由残基本身决定,也受周围残基的影响。因此,采用移动窗口的方法截取蛋白质序列片段。将移动窗口中心位置含有配体结合残基的序列片段定义为正集,否则定义为负集。得到正集片段数为4 589,负集片段数为66 137。由于负集片段数大于正集片段数,约是正集的14倍,本文采用随机抽样的方法,把负集随机分为14组,使每组负集的片段数与正集相等,最后取14次结果的平均值作为最终结果。由于周围环境对结合残基的影响未知,所以滑动窗口长分别选取7,9, 11, 13, 15, 17, 19,并通过计算得出最优窗口长。
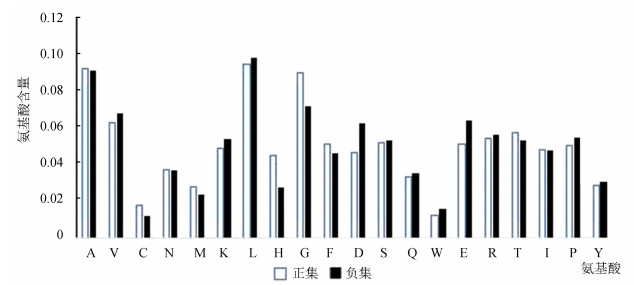
1.2 数据集的统计分析 1.2.1 氨基酸组分信息由文献[17-18]可知,氨基酸组份信息在区分正负集序列片段方面是一个较好的参数,所以我们对HEME正负集序列片段中20种氨基酸组份出现概率进行统计分析(见图 1),空心柱体表示正集,实心柱体表示负集,X轴表示20种氨基酸,Y轴表示相应氨基酸组份在正负集合中出现概率。发现正集片段中G、H、C明显高于负集片段,而E、D则在负集片段中含量明显高于正集片段,同时我们注意到V、K、W、Y也在正负集中差异较大。所以氨基酸组份信息可以作为区分序列片段是参数。
|
图 1 血红素片段正负集氨基酸组份含量 Figure 1 Amino acid composition content of positive and negative sets in hemoglobin fragments |
利用WEBLOGO软件[22],对血红素片段的正负集氨基酸位点保守性信息进行了统计分析,我们以动窗口长度19为例,统计结果(见图 2),横坐标为位点,纵坐标为各位点的氨基酸保守性,氨基酸字母高度代表了在此位点上氨基酸出现的相对频率。正集片段中心即位置10表示血红素配体结合残基,血红素配体结合残基偏好使用L,F,H,R,I等氨基酸,在结合残基附近氨基酸位点保守性都较强。在相同位点处正负集片段保守性有着显著差异,比如对于位置11处正集的偏好残基为G、L、A、T、F等,而负集在这个位点处偏好残基为A、K、V等,再如对于位置12处正集的偏好残基为G、A、L等,而负集在此位点处偏好残基仍为A、K、V等。因此,位点氨基酸保守性信息有助于识别正负集序列片段。

|
图 2 血红素片段正负集氨基酸位点保守性 Figure 2 Position conservation of positive and negative amino acid in hemoglobin fragments |
Fisher判别法在两类识别方面,具有较好的性能[23],该方法已成功应用于蛋白质超二级结构预测[24]。在本文的应用中,以氨基酸组份信息为特征指标为例,考虑正负集每个序列片段上21(20种氨基酸和一个伪氨基酸)维特征指标出现频次;对正负集各4 589个序列片段,统计21个特征指标出现频数。
Xi(1)(xi1(1), xi2(1), ......xin(1)) Xi(2)(xi1(2), xi2(2), .....xin(2)) (i为片段数,n为特征数)
分别计算各指标在正负集中的总体均值、距离、协方差:
| $ \bar{x}_i^{(1)}=\frac{1}{4589} \sum\limits_{k=1}^{4589} x_{k i}^{(1)}, \quad \bar{x}_i^{(2)}=\frac{1}{4589} \sum\limits_{k=1}^{4589} x_{k i}^{(2)} \\ d_i=\bar{x}_i^{(1)}-\bar{x}_i^{(2)} \quad(i=1, 2 \cdots n) \\ \begin{aligned} &S_{i j}=\sum\limits_{k=1}^p\left(x_{k i}^{(1)}-\bar{x}_i^{(1)}\right)\left(x_{k j}^{(1)}-\bar{x}_j^{(1)}\right)+\sum\limits_{k=1}^q\left(x_{k i}^{(2)}-\right. \\ &\left.\bar{x}_i^2\right)\left(x_{k j}^{(2)}-\bar{x}_j^{(2)}\right) \end{aligned} $ |
建立判别函数
| $ F\left(x_1, x_2, \cdots \cdots x_n\right)=C_1 x_1+C_2 x_2+\ldots+C_n x_n $ |
将平均值代入判别函数,计算判别值
| $ \begin{aligned} &\bar{y}^{(1)}=C_1 \bar{x}_1^{(1)}+C_2 \bar{x}_2^{(1)}+\ldots \ldots .+C_n \bar{x}_n^{(1)} \\ &\bar{y}^{(2)}=C_1 \bar{x}_1^{(2)}+C_2 \bar{x}_2^{(2)}+\ldots \ldots+C_n \bar{x}_n^{(2)} \end{aligned} $ |
分界点为
若y1>y2:当y>C, 该片段属于正集片段;当y < C, 该片段属于负集片段;
若y1 < y2:当y>C, 该片段属于负集片段;当y < C, 该片段属于正集片段。
1.3.2 PSSM算法PSSM算法是一种较好的分类方法,被应用于超二级结构预测等研究中并取得了不错的效果[25-26],具体算法如下:
打分函数为:
其中Ci为位点保守性参量:Ci=
其中pi, j为位置概率矩阵的矩阵元:
| $ P_{i . j}=\frac{\left(f_{i, j}+\frac{\sqrt{N_i}}{21}\right)}{\left(N_i+\sqrt{N_i}\right)} $ |
fi, j表示位置频数矩阵的第i列、第j各氨基酸出现的频次Ni表示在第i个位点上出现的氨基酸的总和, fi, max表示位置频数矩阵的第i列的最大值。
以位点氨基酸信息为基础参数,通过训练集构造标准打分矩阵,对于检验集的每条片段,得到两个打分s值,哪个分数高,片段就被判为那个集。同时,打分值也是一个比较好的预测参数,因此本文也把打分值作为预测特征参数用于Fisher计算。
1.3.3 预测结果的评价方法采用5交叉检验,即把两类把样本随机分为5份,每次都选取4/5作训练集,1/5作检验集,交叉进行5次,最后取5次平均结果。
通常结合残疾的识别都采用五交叉检验,并且使用下列评价指标:敏感性(Sn)、特异性(Sp)、总精度(ACC)和相关系数(MCC)表示,分别定义为:
| $ \begin{gathered} S_n=\frac{T P}{T P+F N} S_p=\frac{T N}{T N+F P} \\ A C C=\frac{T P+T N}{T P+T N+F P+F N} \\ M C C=\frac{T P \times T N-F P \times F N}{\sqrt{(T P+F P)(T P+F N)(T N+F P)(T N+F N)}} \end{gathered} $ |
此外,文献[16]中也采用Recal、Prcision、ACC、F1-score、MCC来评价预测结果,其中Recal即上文提到敏感性(Sn),Prcision与F1-score计算方法如下:
| $ \begin{aligned} &\text { Pr}cision =\frac{T P}{T P+F P} \\ &F 1- { score }=\frac{2 \times \text{Re}cal \times \text { Pr}cision }{\text{Re}cal+\text { Pr}cision } \end{aligned} $ |
其中,TP表示正确识别金属离子配体结合残基的数量;FN表示将金属离子配体结合残基识别为非金属离子配体结合残基的数量;TN表示正确识别金属离子配体非结合残基的数量;FP表示将金属离子配体非结合残基识别为金属离子配体结合残基的数量。
2 结果及讨论 2.1 位置权重矩阵打分算法的预测结果及讨论以氨基酸位点保守性为特征指标,使用位置权重矩阵打分算法进行预测,选取移动窗口为7、9、11、13、15、17、19长度,判别结果(见表 1)。从Sn来看移动窗口长度为7、9、11、13时结果较好,都超过到53%;从Sp来看,移动窗口长度为15、17、19时结果较好,都超过81%;移动窗口长度为9、11、13时,预测ACC和MCC结果较好,分别超过了65%和0.32。相对来讲,窗口长度为11时,相关系数为0.32,总精度为65.59%,预测结果较好。另外我们发现使用位置权重矩阵打分算法预测结果不高,但相关系数都大于0.30。
| 表 1 以氨基酸参数位置权重矩阵打分算法判别法判别结果 Table 1 Performance of position weight matrix discrimination algorithm using amino acid as parameter |
以组分氨基酸为特征指标,使用Fisher判别法进行预测。对于每条训练集的序列,都可以得到21(20种氨基酸和一个伪氨基酸)维特征参数,选取移动窗口为7、9、11、13、15、17、19长度,判别结果(见表 2)。发现以氨基酸组份为参数时,从Sn来看7个窗口结果相差不大,相对来讲7、9、11稍好,大约都在61%;从Sp来看,移动窗口选取15、17、19时较好,约在65%以上;ACC和MCC结果也相差不大。相对来讲,窗口长度为9时结果稍好,总精度为63.17%,相关系数为0.32。
| 表 2 以氨基酸参数Fisher判别法判别结果 Table 2 Performance of Fisher discrimination algorithm by the amino acid parameter |
以位点氨基酸保守性信息为特征指标,使用Fisher判别法进行预测,对于每条训练集长度为L的序列,都可以得到21×L维特征参数,选取移动窗口为7、9、11、13、15、17、19长度,判别结果见表 2。以位点氨基酸保守性信息为参数时,发现窗口的改变时Sn、Sp、ACC、MCC这四个指标几乎无太大改变,除了窗口长度为7时MCC略差;相对来讲,移动窗口长度为13、15时预测结果略占优势,总精度67.79%,相关系数0.36。基于同样的特征参数,该预测结果比用位置权重矩阵打分算法要好一些。
2.3 优化特征参数Fisher判别法的预测探索由以上计算结果可知,利用Fisher判别法,以氨基酸组份信息为参数时移动窗口长度为9结果较好,以位点氨基酸保守信息为参数时移动窗口长度为15结果较好,综合这两个指标进行探索,特征参数为15×21+21共336个指标,利用Fisher判别法,判别结果(见表 3)。发现综合位点氨基酸保守信息和氨基酸组份信息时,判别结果和只考虑位点氨基酸保守信息结果无太大差异,可能由于指标参数太多,影响判别结果,所以,考虑先作主成分分析,再进行判别。
| 表 3 不同窗口优化组合判别法判别结果 Table 3 Performance of different window optimization combination discrimination methods |
由前面结果可知,以氨基酸为特征指标,位置权重矩阵打分算法进行预测,移动窗口选取11个氨基酸长度相关系数较高,于是选取氨基酸位置权重矩阵打分与Fisher判别法中氨基酸组份信息的最优窗口组合,进行预测。先用位置权重矩阵打分算法对11个窗口氨基酸进行打分,将两个分数作为特征指标加入到以组份氨基酸为特征指标的9个窗口长度的Fisher判别法中,这样特征指标共23个,判别结果(见表 3)。发现以组分氨基酸为特征指标时,Fisher判别法加入位置权重矩阵打分值以后预测结果有很大提高,相关系数从原来的0.26提高到0.35,说明这两种方法结合有利于预测。如果进一步加入亲疏水性,极性等指标,结果可能会更好。另外以位点氨基酸信息的Fisher判别法用15窗口长度加入11窗口长度的位置权重矩阵打分值,但预测精度没有提高,结果也就没有给出,可能由于特征指标太多影响预测结果,下一步将结合主成分分析进行预测。
2.4 与文献[19]结果比较文献[19]中使用SVM方法,综合了PSSM、RASA、DPX、CX或这些特征的组合构造了15个基于结构的分类器,部分预测结果(见表 4)。比较而言,该方法更为简单。文献[19]中使用的单一指标最好的是PSSM,利用Fisher判别法,使用单一指标最好是氨基酸位点保守性,结果较好一些,综合使用多种指标时,文献[19]结果更好一些,所以下一步工作也考虑综合多个指标进行判别。
3 结论从Biolip数据库中,整理出与血红素结合的蛋白质链,并利用Fisher判别法和位置权重打分矩阵进行识别血红素结合残基。利用Fisher判别法时,考虑20种氨基酸组份信息、位点氨基酸保守信息以及两种信息的优化组合,取得较好预测结果。但与前人工作相比,预测结果稍差,在以后工作中将考虑氨基酸的二级结构信息,亲疏水性、极性等指标进行判别,以进一步提高预测结果。
| [1] |
HU X Z, FENG Z X, ZHANG X J, et al. The identification of metal ion ligand-binding residues by adding the reclassified relative solvent accessibility[J]. Frontiers in Genetics, 2020, 11: 214. DOI: 10.3389.fgene.2020.00214.
(  0) 0) |
| [2] |
HU X Z, GE R, FENG Z X. Recognizing five molecular ligand-binding sites with similar chemical structure[J]. Journal of Computational Chemistry, 2020, 41(2): 110-118. DOI:10.1002/jcc.26077 (  0) 0) |
| [3] |
LIU L, HU X Z, FENG Z X, et al. Prediction of acid radical ion binding residues by K-nearest neighbors classifier[J]. BMC Molecular and Cell Biology, 2019, 20(S3): 52. DOI:10.1186/S12860-019-0238-8 (  0) 0) |
| [4] |
SCHNEIDER S, MARLES-WRIGHT J, SHARP K H, et al. Diversity and conservation of interactions for binding heme in b-type heme proteins[J]. Natural Product Reports, 2007, 24: 621-630. DOI:10.1039/b604186h (  0) 0) |
| [5] |
KENNETH L. An overview on GPCRs and drug discovery: Structure-based drug design and structural biology on GPCRs[J]. Methods in Mollecular Biology, 2009, 552: 51-66. (  0) 0) |
| [6] |
BIKIE D E, BOECHI L, CAPAPECE L, et al. Modeling heme proteins using atomistic simulations[J]. Phys Chem Chem Phys, 2006, 8: 5611-5628. DOI:10.1039/B611741B (  0) 0) |
| [7] |
AJAY A P G, MAURICIO L, BENJAMIN F S. HeMoQuest: A webserver for qualitative prediction of transient heme binding to protein motifs[J]. BMC Bioinformatics, 2020, 21(1): 124. DOI:10.1186/s12859-020-3420-2 (  0) 0) |
| [8] |
TERWILLIGER N B. Functional adaptations of oxygen-transport proteins[J]. Experimental Biology and Medicine, 1998, 201: 1085-1098. (  0) 0) |
| [9] |
REEDY C J, GIBNERY B R. Heme protein assemblies[J]. Chem Rev, 2004, 104: 617-649. DOI:10.1021/cr0206115 (  0) 0) |
| [10] |
MENSE S M, ZHANG L. Heme: A versatile signaling molecule controlling the activities of diverse regulators ranging from transcription factors to MAP kinases[J]. Cell Research, 2006, 16: 681-692. DOI:10.1038/sj.cr.7310086 (  0) 0) |
| [11] |
SCHNEIDER S, MARLES-WRIGHT J, SHARP K H, et al. Diversity and conservation of interactions for binding heme in b-type heme proteins[J]. Nature Product Reports, 2007, 24: 621-630. DOI:10.1039/b604186h (  0) 0) |
| [12] |
EBERT J, ALTMAN R. Robust recognition of zinc binding sites in proteins[J]. Protein Science, 2008, 17(1): 54-65. (  0) 0) |
| [13] |
SOBOLEV V, EDELMAN M. Web tools for predicting metal binding sites in proteins[J]. Israel Journal of Chemistry, 2013, 53(3/4): 166-172. (  0) 0) |
| [14] |
BABOR M, GERZON S, RAVEH B, et al. Prediction of transition metal—binding sites from apo protein structures[J]. Proteins: Structure, Function, and Bioinformatics, 2008, 70(1): 208-217. (  0) 0) |
| [15] |
ZHU Y H, HU J, QI Y. Boosting granular support vector machines for the accurate prediction of protein-nucleotide binding sites[J]. Combinatorial Chemistry & High Throughput Screening, 2019, 22(7): 455-469. (  0) 0) |
| [16] |
YANG J, ROY A, ZHANG Y. BioLiP: A semi-manually curated database for biologically relevant ligand-protein interactions[J]. Nucleic Acids Research, 2013, 41(D1): D1096-D1103. (  0) 0) |
| [17] |
HU X Z, DONG Q W. Recognizing metal and acid radical ion-binding sites by integrating ab initio modeling with template-based transferals[J]. Bioinformatics, 2016, 32(23): btw396. (  0) 0) |
| [18] |
CAO X Y, HU X Z, ZHANG X J, et al. Identification of metal ion binding sites based on amino acid sequences[J]. Plos One, 2017, 12(8): 13. (  0) 0) |
| [19] |
LIU R, HU J. HemeBIND: A novel method for heme binding residue prediction by combining structural and sequence information[J]. BMC Bioinformatics, 2011, 12: 207. DOI:10.1186/1471-2105-12-207 (  0) 0) |
| [20] |
LIU R, HU J. HemeBIND: Computational prediction of Heme-binding residues by exploiting residue interaction network[J]. PLoS One, 2011, 6(10): e25560. DOI:10.1371/journal.pone.0025560 (  0) 0) |
| [21] |
ZHAO Z Q, XU Y H, ZHAO Y. SXGBsite: prediction of protein-ligand binding sites using sequence information and extreme gradient boosting[J]. Genes (Basel), 2019, 10(12): 965. DOI:10.3390/genes10120965 (  0) 0) |
| [22] |
LIU T, LIN Y, WEN X, et al. BindingDB: A web-accessible database of experimentally determined protein-ligand binding affinities[J]. Nucleic Acids Research, 2007, 35: 198-201. DOI:10.1093/nar/gkl999 (  0) 0) |
| [23] |
徐克学. 生物数学[M]. 北京: 科学出版社, 2002: 40-50. XU Kexue. Biological mathematics[M]. Beijing: Science Press, 2002: 40-50. (  0) 0) |
| [24] |
李彩艳. 蛋白质超二级结构库的建立及其序列统计分析[D]. 呼和浩特: 内蒙古工业大学, 2007: 5. LI Caiyan. Construction of a protein supersecondary structure library and sequence statistical analysis[D]. Hohhot: Inner Mongolia University of Technology, 2007: 5. (  0) 0) |
| [25] |
姜雪, 胡秀珍. 打分矩阵方法在β一发夹模体识别中的应用[J]. 生物信息学, 2007(4): 156-158. JIANG Xue, HU Xiuzhen. Application of grade matrix method in the mode identification of β[J]. China Journal of Bioinformatics, 2007(4): 156-158. (  0) 0) |
| [26] |
王春莲, 张晓东. 基于打分矩阵的多类蛋白质折叠子的预测[J]. 生物信息学, 2011(9): 42-45. WANG Chunlian, ZHANG Xiaodong. prediction of multiprotein folding based on scoring matrix[J]. Chinese Journal of Bioinformatics, 2011(9): 42-45. (  0) 0) |
 2022, Vol. 20
2022, Vol. 20


