在遗传学中,转录终止子通常位于poly(A)位点的下游,提供终止转录的信号。它通过对新合成的转录本RNA提供信号来介导转录终止[1-2]。一般来说,原核生物的转录终止子可分为两类:一类依赖于ρ(Rho)因子才能实现终止作用,记作Rho-dependent;另一类则不依赖ρ因子便能实现终止作用,记为Rho-independent。ρ因子是一种解旋酶,可以破坏mRNA-DNA-RNA聚合酶的转录复合体。通常在细菌和噬菌体中发现Rho-dependent转录终止子[3-4]。Rho-independent的终止位点位于翻译终止密码子的下游,由mRNA上一个无结构的、富含GC碱基对的序列组成[5]。Rho-independent[6-7]因子包含7-20个GC-rich区域,后跟一个短poly-T或T-stretch,在延长转录本上形成自退火发夹结构,转录中的RNA聚合酶遇到发夹结构将会暂停前进。它通过破坏mRNA-DNA-RNA聚合酶三元复合物,最终使转录终止。
在传统的实验中,转录终止子是否存在通常是通过测定mRNA的长度来确定的,而这种方法往往无法精确的识别终止位点[8]。因此,许多预测转录终止子的方法被开发出来。近年来,Yada等[9]利用隐马尔可夫模型预测了大肠杆菌基因的转录终止子。Ermolaeva[10]和Unniraman等[11]分别使用TransTerm算法和GeSTer算法预测了转录终止子。2001年,Lesnik等[12]提出了一种基于热力学评分系统预测大肠杆菌K-12基因组终止子的方法。随着机器学习技术的发展,许多分类任务得到了解决。Feng等[8]提取伪k-tuple核苷酸组成特征,并通过二项分布进行特征选择。随后将选择的特征与支持向量机(SVM)相结合,构建了一个名为iTerm-PseKNC[8]的计算方法来预测转录终止子。最近,Fan等[13]采用k核苷酸的位置信息、核苷酸的含量、核苷酸的47种物理化学性质作为特征向量,并结合XGBoost分类算法构建了预测模型iterb-PPse, 取得了相当不错的效果。值得注意的是,原有的预测方法都是采用传统的机器学习方法作为分类算法。近几年,深度学习种的卷积神经网络框架在生物信息领域得到了广泛应用,并且取得了令人满意的分类性能[14-15]。因此,我们尝试将卷积神经网络应用于细菌终止子的预测。
在本研究中,根据Feng等[8]的工作,引入了一种新的转录终止子预测模型, 称为TermCNN。首先从大肠杆菌DNA序列中提取k-mer (k= 4, 5, 6, 7)核苷酸组成特征作为CNN的输入向量。在五折交叉验证中,挑选出准确率最高的6-mer核苷酸组成特征。然后采用最大相关-最大距离(MRMD)、二项分布和F-score这三种特征选择方法来寻找6-mer特征的最优特征子集,以减少无用信息和节省运行时间。最后将选择出的最优特征子集与电子-离子相互作用伪电位(EIIP)特征相结合,输入到CNN进行训练,构建高精度模型。五折交叉验证以及五个独立测试数据集的实验结果一致显示了本文提出的预测模型TermCNN的有效性,特别是用于区分不同种类的终止子。
1 材料和方法 1.1 数据收集和预处理一个客观的基准数据集是建立终止子预测模型的基础。从RegulonDB[16]中收集大肠杆菌的终止子,去冗余后得到286个Rho-independent终止子和19个Rho-dependent终止子[8]。与之前的数据集相比,RegulonDB新增了25个转录终止子。将新发现的25个转录终止子视为一个独立的测试集,命名为E_Ter_25。对于训练数据集,采用了与Feng[8]相同的数据集,包含280个终止子和560个非终止子,便于评估和比较不同预测器的性能。对于独立测试,Feng [8]使用了两个终止子独立测试集,分别是E_Ter_147和B_Ter_425。从Fan等[13]的工作中选取两个均为负样本构成的独立测试集,样本是分别从大肠杆菌和枯草芽孢杆菌的上游截取的,记为E_Nonter_159和B_Nonter_122。在缩写中,E表示来自大肠杆菌的序列,B表示来自枯草芽孢杆菌的序列,数字表示每个数据集中的样本数量(见表 1)。
| 表 1 不同物种的数据集 Table 1 Datasets of different species |
特征提取在开发基于机器学习算法的计算模型中起着非常重要的作用。本文从序列中提取了两类特征:一个是k-mer,另一个是EIIP[17]。
1.2.1 k-mer核苷酸组成给出一个DNA序列D,它的直观表达式是[18]:
| $ D=R_1 R_2 R_3 R_4 R_5 R_6 R_7 \cdots R_L $ | (1) |
其中Ri表示在DNA序列中第i个位置的核苷酸。
k-mer核苷酸是将DNA序列转化为数字向量的一种简单而常用的方法,这一方法具有重要的生物学意义,在DNA调控元件识别中已得到了广泛的应用[19-23]。k-mer可以将任何DNA序列表示为4k维的向量如下:
| $ R=\left[\varphi_1 \varphi_2 \cdots \varphi_u \cdots \varphi_{4^k}\right] $ | (2) |
其中φu(u=1, 2…, 4k)为沿着序列第u个k-mer的频率。在本工作中,k=1、2、3、4、5、6、7,并与EIIP相结合进行测试,寻找最优的特征集。
1.2.2 EIIPEIIP作为特征已被广泛的用来预测基因序列[17]。基于EIIP的识别方法广泛应用于基因结构识别的关键部分,如F56F11.4基因的预测[24]、囊性纤维化基因的预测和和增强子的识别[25]等。
四个核苷酸的EIIP值分别为,A: 0.126,G: 0.0806,C: 0.134,T: 0.133。计算每条序列中A、T、G、C的平均EIIP值,构造特征向量为[25]:
| $ P=\left[E I I P_{A A A} \cdot f_{A A A}, E I I P_{A A C} \cdot f_{A A C}, \cdots, E I I P_{T T T} \cdot f_{T T T}\right] $ | (3) |
其中fXYZ为任意三核苷酸XYZ的频率,EIIPXYZ是三核苷酸XYZ的EIIP值之和,X, Y, Z∈{A, C, G, T}。
1.3 特征选择特征选择方法可以降低特征向量的维数,为训练分类器找到最优特征子集。近几年,最大相关-最大距离(MRMD)[26]、F-score[27]和二项分布(BD)[28],方法在改善预测器性能上具有显著成效,已广泛应用于生物信息学领域。
1.3.1 MRMDMRMD利用皮尔逊相关系数计算特征子集与目标类的相关性,并使用欧氏距离函数计算特征子集的冗余度,相关性与距离的和最大的特征被选择到最终的特征子集中。首先定义两个向量的相关系数如下:
| $ \operatorname{PCC}(\vec{X}, \vec{Y})=\frac{S_{\vec{X} \vec{Y}}}{S_{\vec{X}} S_{\vec{Y}}} $ | (4) |
其中,
| $ S_{\vec{X} \vec{Y}}=\frac{1}{N-1} \sum\limits_{k=1}^N\left(x_k-\bar{x}\right)\left(y_k-\bar{y}\right) $ | (5) |
| $ S_{\vec{X}}=\sqrt{\frac{1}{N-1} \sum_{k=1}^N\left(x_k-\bar{x}\right)^2} $ | (6) |
| $ S_{\vec{Y}}=\sqrt{\frac{1}{N-1} \sum_{k=1}^N\left(y_k-\bar{y}\right)^2} $ | (7) |
| $ \bar{x}=\frac{1}{N} \sum\limits_{k=1}^N x_k $ | (8) |
| $ \bar{y}=\frac{1}{N} \sum\limits_{k=1}^N y_k $ | (9) |
这里xk, yk是向量
从而,第i个特征的最大相关值MR定义为:
| $ \max M R_i=\left|P C C\left(\vec{F}_i, \vec{C}_i\right)\right|(1 \leqslant i \leqslant M) $ | (10) |
其中
本文中,两个特征的距离采用欧式距离,定义如下:
| $ E D(\vec{X} \vec{Y})=\sqrt{\sum _{k=1}^N\left(x_k-y_k\right)^2} $ | (11) |
其中,xk, yk是向量
最大距离就是取所有欧氏距离中的最大值,记为:
| $ \max M D_i=E D_i(1 \leqslant i \leqslant M) $ | (12) |
根据以上结果,第i个特征MRMD值定义为max(MRi+MDi),根据此值的大小,对特征进行排序。数值越大,表明此特征与目标标签的相关性越强[26]。
1.3.2 F-score第j个特征的F-score定义为:
| $ F {-score }(j)=\frac{\left(\bar{x}_j^{(+)}-\bar{x}_j\right)^2+\left(\bar{x}_j^{(-)}-\bar{x}_j\right)^2}{\frac{1}{m^{+}-1} \sum _{k=1}^{m^{+}}\left(\bar{x}_{k, j}^{(+)}-\bar{x}_j^{(+)}\right)^2+\frac{1}{m^{-}-1} \sum _{k=1}^{m^{-}}\left(\bar{x}_{k, j}^{(-)}-\bar{x}_j^{(-)}\right)^2} $ | (13) |
其中xj,xj(+)和xj(-)分别表示全部、正、负数据集中第j个特征的平均值。m+和m-是正样本和负样本的数目。xk, j(+)和xk, j(-)分别表示第k个正样本和第k个负样本的第j个特征。F-score值越大,说明特征越有用。
1.3.3 二项分布Feng[8]和Su[29]采用基于二项分布的技术,通过SVM分类器进行五折交叉验证的性能结果对特征进行选择。这里,先验概率qi定义为k-mer核苷酸的频率,如下所示:
| $ q_i=\frac{m_i}{M} $ | (14) |
其中mi(i=1, -1)分别表示正、负训练数据集(即终止子和非终止子数据集)中的k-mer片段总数。M为全部训练数据集中k-mer片段的总数。因此,第j个k-mer核苷酸(j=1, 2, …, 4k)在正样本和负样本中的概率可以定义为:
| $ p\left(n_{1, j}\right)=\sum\limits_{m=n_{1 j}}^{N_j} \frac{N_{j} !}{m !\left(N_j-m\right)} q_i^m\left(1-q_i\right)^{N_j-m} $ | (15) |
| $ p\left(n_{-1, j}\right)=\sum\limits_{m=n-_{1 j}}^{N_j} \frac{N_{j} !}{m !\left(N_j-m\right)} q_i^m\left(1-q_i\right)^{N_j-m} $ | (16) |
其中Nj表示终止子和非终止子训练数据集中第j个k-mer核苷酸的总数。n1, j和n-1, j分别表示正、负训练数据集中第j个k-mer核苷酸的总数。
最后,根据以下公式计算训练数据集中的第j个k-mer核苷酸的概率:
| $ P_j=\min \left(p\left(n_{1, j}\right), p\left(n_{-1, j}\right)\right. $ | (17) |
所有的k-mer核苷酸可以根据概率的大小进行排序,也就是说,Pj越小,相应的k-mer核苷酸对分类效果越有效。
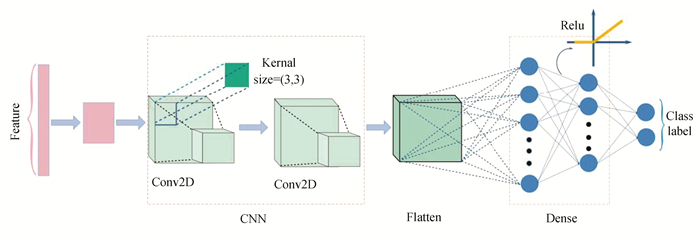
2 卷积神经网络CNN已被广泛应用于各种分类任务中,其在图像识别、图像检测、语音识别等方面表现出良好的性能。随着深度学习的深入研究[30],CNN还用于预测启动子[31]、蛋白质泛素化位点[32]、蛋白质翻译后修饰位点的capsule网络[33]、RNA假尿苷位点[34]。在本研究中,借助Keras工具,使用CNN模型识别转录终止子。TermCNN由两个卷积层、两个池化层和连接层组成(见图 1)。转录终止子包含更多的GC碱基对,因此使用了一个平均池化层,池化大小为3×3,这适合于获取序列的GC含量。还使用dropout来防止模型的过拟合。对于随机梯度下降法,选择了Adam优化算法。整个程序在Python 3.6中使用,实验环境为:主机CPU型号为AMD Ryzen 74 800 H with Radeon Graphics,主频为2.90 GHz,物理内存为16 GB,操作系统为64位Windows10,深度学习框架为TensorFlow 2.0.0。
|
图 1 神经网络模型的架构 Figure 1 Architecture of neural network model |
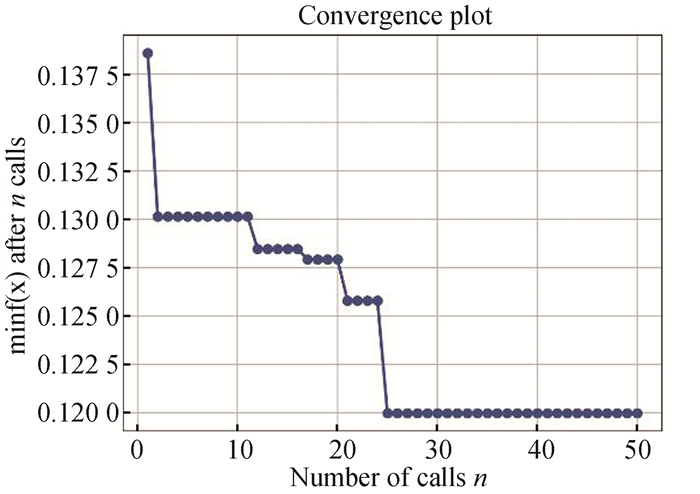
采用贝叶斯对卷积神经网络的神经元个数(a)、批次(b)、dropout(c)、学习率(d)、激活函数(e)以及全连接层数(f)这六种参数进行优化。除上述参数外,所涉及到的其它参数均按照scikit-learn库的默认值。其中a在[8, 64]中取值,b在集合[8, 128]中取值,c在集合{0.1, 0.3, 0.5, 0.7}中取值,d在集合[0.000 1, 0.01]中取值,e的选取有两种情况relu和sigmoid,f在集合[1, 10]中取值。根据贝叶斯优化方法对参数组合进行五十次寻优,耗时1小时11分钟,优化过程以及最佳参数结果(见图 2)。贝叶斯优化器建立了搜索空间的替代模型,并在此维度内进行搜索,而不是在实际搜索空间内进行搜索。优化参数的二维图,最终选取损失值最小(0.122 5)的参数组合。
|
图 2 参数选择的结果 Figure 2 Results of parameters selection |
为了评估转录终止预测模型的性能,使用准确性(Acc)、灵敏度(Sn)、特异性(Sp)和马修相关系数(MCC)作为五折交叉验证和独立数据集测试的评估标准。
| $ \left\{\begin{array}{c} S p=\frac{T N}{T N+F P} \\ S n=\frac{T P}{F N+T P} \\ A c c=\frac{T P+T N}{F N+T P+T N+F P} \\ M C C=\frac{T P \times T N-F P \times F N}{\sqrt{(T N+F N)(T N+F P)(T P+F N)(T P+F P)}} \end{array}\right. $ | (18) |
其中TP、TN、FP和FN分别代表真阳性、真阴性、假阳性和假阴性的数量。
4 结果分析 4.1 选择最优的特征子集为寻找使CNN分类器达到最优性能的k-mer(k=4, 5, 6, 7)特征,利用五折交叉验证对每类特征进行测试。如图 3所示,6-mer与CNN的整合得到了最好的MCC和Acc。6-mer的MCC值为0.942,比4-mer高0.101,比5-mer高0.004,比7-mer高0.035。考虑到6-mer的特征维数为4096,高维度特征可能包含冗余信息,导致过拟合。因此,使用了MRMD、F-Score和二项分布这三种常用的特征选择方法来寻找最优特征子集。

|
图 3 四种具有不同数量特征的模型性能 Figure 3 Performance of four models with different numbers of features |
第1步,根据F-score值、MRMD值和二项分布值对6-mer向量中的4 096个元素进行排序;
第2步,设k=30作为初值。需要指出的是,为特征子集选择的维数是某个数字k的平方,特征向量可以转换成一个方阵作为输入。因此,选取排名靠前的k2-64元素与EIIP特征结合形成长度为k的方0阵,然后将一维特征向量转换为二维方阵作为CNN的输入。
以步长为5,在特征方阵长度为k+5,通过五折交叉验证寻找准确率最高的特征子集。最后在精度最高的特征维数周围使用步长为1筛选出最优特征子集。并比较最优特征集和无特征选择的特征集的结果。对于F-score、二项分布和MRMD,k值分别为63、64和51时的准确率最高。相对时间成本和准确性,将MRMD方法选择的6-mer特征向量中前2 537个元素与64个EIIP特征相结合,Acc为97.62%,Sn为92.86%,Sp为100%,MCC为0.947。这表明所建立的模型TermCNN具有良好的识别转录终止子的能力。
4.2 模型对比为了证明使用深度学习识别转录终止子的优越性,将CNN与决策树、多层感知器、逻辑回归、朴素贝叶斯、基于SVM的iTerm-PseKNC、iterb-PPSE和CNN+LSTM进行了比较。结果如表 2所示。可见,在浅层机器学习中,基于SVM的iTerm-PseKNC达到了最好的Acc(95.71%),MCC(0.888),CNN实现了较好的性能,达到97.98%的Acc和0.955的MCC,但是基于XGBoost的iterb-PPse给出了最好的结果,Acc为99.88%,MCC为0.999。TermCNN比iterb-PPse稍微逊色的原因有两个:1)提取的特征过于单一。本文仅仅考虑的终止子序列的6-mer特征,没有考虑位置及核苷酸的物理化学性质;2)数量的样本数量较少,不能够体现CNN的优越性。随着越来越多终止子序列的发现,也将会继续优化我们的模型。
| 表 2 不同分类器在五折交叉验证中识别终止子的比较 Table 2 Comparison of different classifiers for identifying terminators on 5-fold cross-validation |
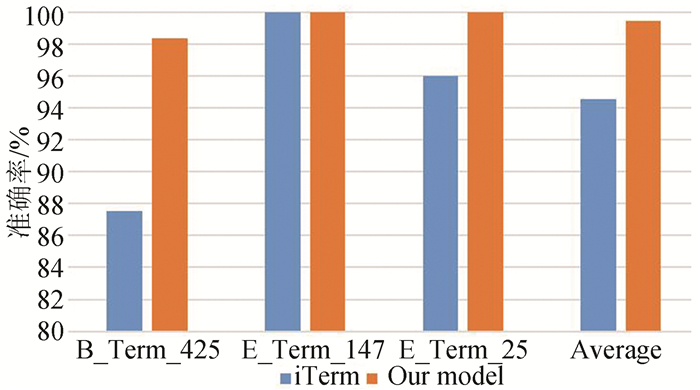
为了更好地评价模型的泛化能力,进一步测试了五个独立的数据集E_Ter_147、B_Ter_425,E_Ter_25,E_Nonter_159和B_Nonter_122。对于E_Ter_147,TermCNN正确预测了147个终止子,iTerm-PseKNC也正确预测了147个终止子。对于B_Ter_425,TermCNN型正确预测了417个终止子(98.12%),而iTerm-PseKNC仅正确预测了372个终止子(87.53%)。对于新的独立测试集,TermCNN正确预测了所有25个终止子(100%),而iTerm-PseKNC正确预测了24个终止子(96%),如图 4所示。为了多方面检验所建立模型的有效性,从iterb-PPse中选取两个负样本数据集E_Nonter_159和B_Nonter_122。对于E_Nonter_159,TermCNN预测了158个非转录终止子(99.37%)。对于B_Nonter_122,TermCNN预测了121个非转录终止子(99.18%)。相比于iterb-PPse, TermCNN预测对的数目少一个。比较遗憾的是,由于iTerm-PseKNC提供的网络服务器不能正常使用,因此无法和它进行比较。
|
图 4 在独立测试中模型与iTerm-PseKNC的准确率比较 Figure 4 Accuracy comparison between iTerm-PseKNC and proposed model on independent datasets |
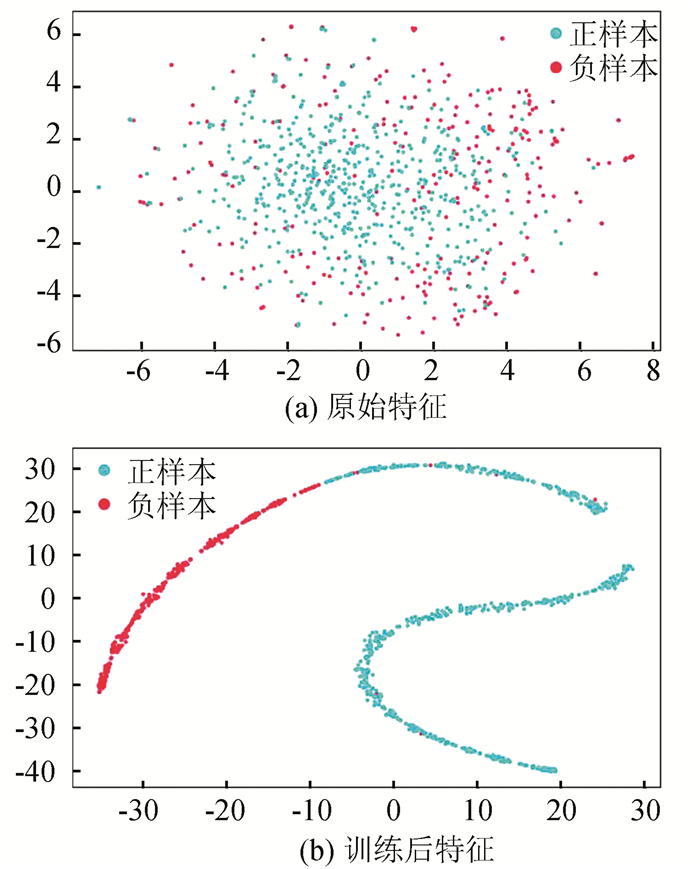
为了更加直观的可以看到特征的有效性,通过采用t分布随机邻居嵌入(t-SNE)进行特征可视化。图 5中每个点代表一个样本,蓝色点表示转录终止子位点,红色点表示非转录终止子位点。一开始可以清晰的看到只用原始特征表示的两类点很难分开,后经过神经网络层层训练,在全连接层的输出向量可以比较明显的划分两类。因此,显示CNN处理转录终止子数据很有效。
|
图 5 t-SNE可视化特征表示 Figure 5 t-SNE visualization for feature representation |
1) 在这项研究中,提出了一种新的计算模型TermCNN可以快速准确地识别转录终止子;
2) 将代表性的6-mer特征子集和EIIP作为输入参数,利用CNN对模型进行训练和优化;
3) 五折交叉验证和多个独立测试结果证明了模型的竞争力,其性能结果明显优于其他算法和现有计算工具iTerm-PseKNC,但是在灵敏度方面比iterb-PPse稍低。
| [1] |
RICHARDSON J P, ROBERTS J W. Transcription termination[J]. Critical Reviews in Biochemistry and Molecular Biology, 1993, 28(1): 1-30. DOI:10.3109/10409239309082571 (  0) 0) |
| [2] |
HENKIN T M. Control of transcription termination in prokaryotes[J]. Annual Review of Genetics, 1996, 30(1): 35-57. DOI:10.1146/annurev.genet.30.1.35 (  0) 0) |
| [3] |
RICHARDSON J P. Rho-dependent termination and atpases in transcript termination[J]. Biochimica et Biophysica Acta, 2002, 1577(2): 251-260. DOI:10.1016/S0167-4781(02)00456-6 (  0) 0) |
| [4] |
RICHARDSON J P. Loading rho to terminate transcription[J]. Cell, 2003, 114(2): 157-159. DOI:10.1016/s0092-8674(03)00554-3 (  0) 0) |
| [5] |
CIAMPI M S. Rho-dependent terminators and transcription termination[J]. Microbiology, 2006, 152(9): 2515-2528. DOI:10.1099/mic.0.28982-0 (  0) 0) |
| [6] |
NUDLER E, GOTTESMAN M E. Transcription termination and anti-termination in E. coli[J]. Genes to Cells, 2002, 7(8): 755-768. DOI:10.1046/j.1365-2443.2002.00563.x (  0) 0) |
| [7] |
YACHIE N, ARAKAWA K, TOMITA M. On the interplay of gene positioning and the role of Rho-independent terminators in Escherichia coli[J]. FEBS Letters, 2006, 580(30): 6909-6914. DOI:10.1016/j.febslet.2006.11.053 (  0) 0) |
| [8] |
FENG C Q, ZHANG Z Y, ZHU X J, et al. iTerm-PseKNC: A sequence-based tool for predicting bacterial transcriptional terminators[J]. Bioinformatics, 2019, 35(9): 1469-1477. DOI:10.1093/bioinformatics/bty827 (  0) 0) |
| [9] |
YADA T, NAKAO M, TOTOKI Y, et al. Modeling and predicting transcriptional units of Escherichia coli genes using hidden Markov models[J]. Bioinformatics, 1999, 15(12): 987-93. DOI:10.1093/bioinformatics/15.12.987 (  0) 0) |
| [10] |
ERMOLAEVA M D, KHALAK H G, WHITE O, et al. Prediction of transcription terminators in bacterial genomes[J]. Journal of Molecular Biology, 2000, 301(1): 27-33. DOI:10.1006/jmbi.2000.3836 (  0) 0) |
| [11] |
UNNIRAMAN S, PRAKASH R, NAG-ARAJA V. Conserved economics of transcription termination in eubacteria[J]. Nucleic Acids Research, 2002, 30(3): 675-684. DOI:10.1093/nar/30.3.675 (  0) 0) |
| [12] |
LESNIK E A, SAMPATH R, LEVENE H B, et al. Prediction of Rho-independenttranscriptional terminators in Escherichiacoli[J]. Nucleic Acids Research, 2001, 29(17): 3583-3594. DOI:10.1093/nar/29.17.3583 (  0) 0) |
| [13] |
FAN Y, WANG W, ZHU Q. iterb-PPse: Identification of transcriptional terminators in bacterial by incorporating nucleotide properties into PseKNC[J]. PLoS One, 2020, 15(5): 1-19. DOI:10.1371/journal.pone.0228479 (  0) 0) |
| [14] |
LIU K, CAO L, DU P, et al. im6A-TS-CNN: Identifying the N(6)-methyladenine site in multiple tissues by using the convolutional neural network-ScienceDirect[J]. Molecular Therapy - Nucleic Acids, 2020, 21: 1044-1049. DOI:10.1016/j.omtn.2020.07.034 (  0) 0) |
| [15] |
RAMZAN U, HIROYUKI K, LI Y, et al. Promoter analysis and prediction in the human genome using sequence-based deep learning models[J]. Bioinformatics, 2019, 35(16): 2730-2737. DOI:10.1093/bioinformatics/bty1068 (  0) 0) |
| [16] |
SOCORRO G C, HELADIA S, ALBERTO S Z, et al. RegulonDB version 9.0: High-level integration ofgene regulation, coexpression, motif clustering and beyond[J]. Nucleic Acids Research, 2016, 44(D1): D133-D143. DOI:10.1093/nar/gkv1156 (  0) 0) |
| [17] |
NAIR A S, SREENADHAN S P. A coding measure scheme empoying electron-ion interactionpseudo potential (EⅡP)[J]. Bioinformation, 2006, 1(6): 197-202. (  0) 0) |
| [18] |
CHEN W, LIN H, CHOU K C. Pseudo nucleotide composition or PseKNC: An effective formulation for analyzing genomic sequences[J]. Molecular BioSystems, 2015, 11(10): 2620-2634. DOI:10.1039/c5mb00155b (  0) 0) |
| [19] |
GHANDI M, LEE D, MOHAMMAD-NOORI M, et al. Enhanced regulatory sequence prediction using gapped k-mer features[J]. PLoS Computational Biology, 2014, 10(7): e1003711. DOI:10.1371/journal.pcbi.1003711 (  0) 0) |
| [20] |
ZHANG M, LI F, MARQUEZ-LAGO T T, et al. MULTiPly: A novel multi-layer pr-edictor for discovering general and specific types of promoters[J]. Bioinformatics, 2019, 35(17): 2957-2965. DOI:10.1093/bioinformatics/btz016 (  0) 0) |
| [21] |
JIA C, YANG Q, ZOU Q. NucPosPred: Predicting species-specific genomic nucleosome positioning via four different modes of general PseKNC[J]. Journal of Theoretical Biology, 2018, 450: 15-21. DOI:10.1016/j.jtbi.2018.04.025 (  0) 0) |
| [22] |
YI H C, YOU Z H, ZHOU X, et al. ACP-DL: A deep learning long short-term memory model to predict anticancer peptides using high-efficiency feature representation[J]. Molecular Therapy Nucleic Acids, 2019, 17(9): 1-9. DOI:10.1016/j.omtn.2019.04.025 (  0) 0) |
| [23] |
MANAVALAN B, BASITH S, SHIN T H, et al. Meta-4mCpred: A sequence-based meta-predictor for accurate DNA 4mC site prediction using effective feature representation[J]. Molecular Therapy Nucleic Acids, 2019, 16: 733-744. DOI:10.1016/j.omtn.2019.04.019 (  0) 0) |
| [24] |
DEERGHA R D, SWARNY M N S. Analysis ofgenomics and proteomics using DSP techniques[J]. IEEE Transactions on Circuits and Systems I Regular Papers, 2008, 55(1): 370-378. DOI:10.1109/TCSI.2007.910541 (  0) 0) |
| [25] |
HE W, JIA C. EnhancerPred2.0: Predicting enhancers and their strength based on position-specific trinucleotide propensity and electron-ion interaction potentialfeature selection[J]. Molecular Biosystems, 2017, 13(4): 767-774. DOI:10.1039/C7MB00054E (  0) 0) |
| [26] |
ZOU Q, ZENG J, CAO L, et al. A novel features ranking metric with application to scalable visual and bioinformatics data classification[J]. Neurocomputing, 2016, 173(2): 346-354. DOI:10.1016/j.neucom.2014.12.123 (  0) 0) |
| [27] |
BUI V M, WENG S L, LU C T, et al. SOHSite: Incorporating evolutionary information and physicochemical properties to identify protein S-sulfenylation sites[J]. BMC Genomics, 2016, 17(1): 1-9. DOI:10.1186/s12864-015-2299-1 (  0) 0) |
| [28] |
LAI H Y, CHEN X X, CHEN W, et al. Sequence-based predictive modeling to identify cancerlectins[J]. Oncotarget, 2017, 8(17): 28169-28175. DOI:10.18632/oncotarget.15963 (  0) 0) |
| [29] |
SU Z D, HUANG Y, ZHANG Z Y, et al. iLoc-lncRNA: Predict the subcellular location of lncRNAs by incorporating octamer composition into general PseKNC[J]. Bioinformatics, 2018, 34(24): 4196-4204. DOI:10.1093/bioinformatics/bty508 (  0) 0) |
| [30] |
谢娟英, 刘然. 基于深度学习的目标检测算法研究进展[J]. 陕西师范大学学报(自然科学版), 2019, 47(5): 1-9. XIE Juanying, LIU Ran. Research progress of object detection algorithm based on deep learning[J]. Journal of Shaanxi Normal University (Natural Science Edition), 2019, 47(5): 1-9. DOI:10.15983/j.cnki.jsnu.2019.05.151 (  0) 0) |
| [31] |
UMAROV R, KUWAHARA H, LI Y, et al. Promoter analysis and prediction in the human genome using sequence-baseddeep learning models[J]. Bioinformatics, 2019, 35(16): 2730-2737. DOI:10.1093/bioinformatics/bty1068 (  0) 0) |
| [32] |
FU H, YANG Y, WANG X, et al. DeepUbi: A deep learning framework for prediction of ubiquitination sites in proteins[J]. BMC Bioinformatics, 2019, 20(1): 1-10. DOI:10.1186/s12859-019-2677-9 (  0) 0) |
| [33] |
WANG D, LIANG Y, XU D. Capsule network for protein post-translational modification site prediction[J]. Bioinformatics, 2018, 35(14): 2386-2394. DOI:10.1093/bioinformatics/bty977 (  0) 0) |
| [34] |
TAHIR M, TAYARA H, CHONG K T. iPseU-CNN: Identifying RNA pseudouridine sites using convolutional neural networks[J]. Molecular Therapy Nucleic Acids, 2019, 16: 463-470. DOI:10.1016/j.omtn.2019.03.010 (  0) 0) |
 2022, Vol. 20
2022, Vol. 20


