理论和实验表明突触后局部电位是突触可塑性的关键要素[1-5]。因为只有大而持久的局部去极化才能削弱镁离子对NMDAR受体(N-methyl-D-aspartic acid receptor)的电压依赖性阻滞作用[6-7],导致超线性钙离子内流,诱发LTP[8-10]。但是对于功能连接模式而言,由于其影响因素众多,所以改变功能连接的关键要素还有待探究。实验表明,突触位置对功能连接有影响[11]。近端突触权重由刺激使胞体去极化的能力决定,而远端突触权重由引起局部去极化的能力决定[12]。突触分布对皮层连接也有影响[13]。时空范围内更近的突触输入能引起更大的兴奋性突触后电位(Excitatory-post-synaptic potential, EPSP),导致幅值更大的长时程增强(Long-term potentiation, LTP)[14]。此外,不同刺激模式也能改变神经元连接[5]。脉冲数量固定时,由于随配对频率增大,反向传播动作电位(Back-propagating action potential, bAP)侵入树突的能力下降[11],而EPSP随局部电压累积而增大[9],因此LTP与刺激频率呈现倒“U”形相关性[4]。这些影响因素的共同特征是改变突触可塑性以使连接模式改变,由于突触可塑性主要受突触后局部电位影响,因此局部电位是影响功能连接模式的关键。
由于Hebbian学习规则使突触权重以正反馈形式变化,导致权重失控[15],所以部分模型采用硬边界[16]。例如,Zenke等人的多个可塑性机制协调作用的突触模型[17]以及Chistiakova等人的脉冲时刻依赖可塑性规则(Spike-timing-dependent plasticity, STDP)与异突触可塑性协调控制的突触模型[18]。但硬边界使突触权重增长速率在边界突变,这不符合生物神经系统特征,而利用BCM(Bienenstock-Cooper-Munro)理论和稳态可塑性取消硬边界设计更符合生物神经系统特征[19-20]。BCM模型通过修改LTP阈值获得突触权重稳定性,该阈值取决于突触后活动的平均值[20]。Clopath等人的软边界设计思路与BCM模型在结构上有相似性[21],他们也将权重抑制项设为线性函数,并将增强项设为与突触后变量相关的二次函数。而Carlson等人基于突触后刺激频率的突触模型在可塑性方式上有所不同,是通过整体突触缩放使突触稳定[22],但自平衡突触缩放的时间尺度比关联可塑性(Associative plasticity)慢了至少两个数量级,因此不适合同步抑制Hebbian学习规则诱导的权重失控[18]。软边界模型使突触可塑性更符合神经元的电生理学特征,因此,利用主导功能连接模式的局部电位建立软边界突触可塑性规则是很有意义的。
在Bono与Clopath的神经元模型[23]基础上改进突触可塑性规则,使连接权重与神经元能量状态相联系,能量状态取决于局部膜电位与膜电流密度,由于膜电流密度是局部电位的函数,因此连接权重由局部电位决定。当突触连接接近饱和时,权重遵循稳态可塑性,其增长速率减缓,实现了软边界设计。在不同刺激模式下用该模型观察局部电位与突触权重,通过研究局部电位为亚阈值和超阈值时的功能连接模式,发现两个神经元的突触电位都处于亚阈值时,不产生连接。单向连接只需单个神经元突触后电位超阈值,因此最容易产生。双向连接只在两个神经元局部去极化都超过阈值电位后产生。这些结果对动物皮层以单向连接为主的功能连接模式[21]提供了解释。
1 材料与方法 1.1 仿真环境与模型本文使用Bono和Clopath基于Brian2开发的生物物理学神经元和突触模型[23]。对小鼠视皮层第5层锥体神经元的模拟在Python中的Brian2神经元模拟器上进行[24]。
1.2 电压依赖的突触可塑性模型稳定神经网络中,神经元单个脉冲平均能唤起另一神经元的单个脉冲[25]。实验证明,在清醒与轻度麻醉小鼠初级视皮层上刺激单神经元,只有小部分(< 0.75%)细胞产生脉冲[26-27]。证明稳定神经网络通过动作电位、突触传递、改变突触特性等方式维持能量稳定。由于神经网络由神经元构成,且神经元正常运转离不开稳定的跨膜离子梯度,因此神经元也可以通过维持能量稳定来达到稳态可塑性。本文规定神经元有静息能量状态与脉冲能量状态,脉冲状态的神经元消耗代谢能进行主动转运使能量趋于静息状态,例如将AMPAR受体(α-amino-3-hydroxy-5-methyl-4-isoxazole-propionicacid receptor)插入突触中,改变突触可塑性[28]。能量恢复过程与突触强度变化的关系是,脉冲状态大于静息状态时,遵循稳态可塑性,突触强度衰减,产生长时程抑制(Long-term depression, LTD);脉冲状态低于静息状态时,遵循Hebbian可塑性,突触强度增强,产生LTP。脉冲状态近似静息状态时,突触权重不变。具体公式如下:
| $ W_{j}=A\left(E r_{j}-E_{j}\right) $ | (1) |
其中Wj是突触j的权重,A是标度因子,大小为0.062 5,Erj和Ej是突触后j单位膜的静息和脉冲状态。Erj与Ej无量纲。方程(1)的微分表达式为:
| $ \frac{\mathrm{d} W_{j}}{\mathrm{~d} t}=A\left(\frac{\mathrm{d} E r_{j}}{\mathrm{~d} t}-\frac{\mathrm{d} E_{j}}{\mathrm{~d} t}\right) $ | (2) |
用突触后局部电位和电流密度来表征能量状态,构造突触可塑性函数:
| $ \frac{\mathrm{d} W_{j}}{\mathrm{~d} t}=A\left[\left(_{h}-v_{m}\right) f_{j}\left(v_{m}\right) g_{j}\left(I_{m}\right)-\left(v_{m}-{ }_{h}\right) f_{j}\left(v_{m}\right) g_{j}\left(I_{m}\right)\right] $ | (3) |
Θ(x)为Heaviside函数,Θ(x)=1表示x≥0。Θ(x)=0表示x < 0。θh是脉冲阈值电位,大小为θh=-55 mV。fj(vm)是驱动电位的方程,gj(Im)是驱动电流的函数。Θ(θh-vm)fj(vm)gj(Im)是静息状态的时间导数项,即式(2)的
为使突触权重具有自平衡可塑性,借鉴BCM规则定义驱动电位方程fj(vm)[21],驱动电位是膜电位vm的函数:
| $ f_{j}\left(v_{m}\right)={sign}\left(v_{m}\right)\left|v_{m}-\theta_{l}\right| $ | (4) |
变量vm是突触后局部电位,θl为驱动阈值电位,取θl=-68.5 mV。
驱动电流采用内稳态可塑性,突触后膜电流密度Im不超过某一阈值Imax时,驱动电流等于Im。Im的绝对值大于Imax后,驱动电流呈指数下降。这与最近对突触后膜电流密度的研究结果吻合[29-31]。具体公式如下所示:
| $\begin{array}{l} g_{j}\left(I_{m}\right)=\\ \left\{\begin{array}{c}I_{m}, \left|I_{m}\right|<I_{\max } \\ I_{\max } {sign}\left(I_{m}\right) \exp \left[D\left(I_{\max }-\left|I_{m}\right|\right)\right], \left|I_{m}\right| \geqslant I_{\max }\end{array}\right. \end{array} $ | (5) |
Im是突触后膜电流密度,Imax是突触后膜最大电流密度,取Imax=3 pA/μm2。参数D为阻尼系数,取D=0.05。需要强调,本文构建的虽然是电压依赖可塑性规则,但并不妨碍使用变量Im,因为Im由泄露电流Ilink与活跃电流Iactive组成,它们都是局部电位的函数:
| $ \left\{\begin{array}{c} I_{m}=I_{\text {link }}+I_{\text {active }} \\ I_{\text {link }}=g_{\text {link }} *\left(E_{\text {rest }}-v_{m}\right) \\ I_{\text {active }}=g_{\mathrm{Na}} *\left(E_{\mathrm{Na}}-v_{m}\right)+g_{\mathrm{Ca}} *\left(E_{\mathrm{Ca}}-v_{m}\right)+ \\ g_{\mathrm{K}} *\left(E_{\mathrm{K}}-v_{m}\right) \end{array}\right. $ | (6) |
Im是突触后膜电流密度,Ilink是泄露电流,Iactive为活跃电流。glink、gNa、gCa与gK分别是泄露电导、钠离子电导、钙离子电导以及钾离子电导,这些参数是膜电位的函数。Erest、ENa、ECa、EK为静息电势、钠离子电势、钙离子电势以及钾离子电势,分别等于-60 mV、60 mV、140 mV以及-80 mV。vm为突触后局部电位。由此可见,突触后电流密度Im是突触后膜电位vm的函数,因此突触后电流密度Im与局部电位vm组成的能量依赖可塑性规则本质是电压依赖可塑性规则。
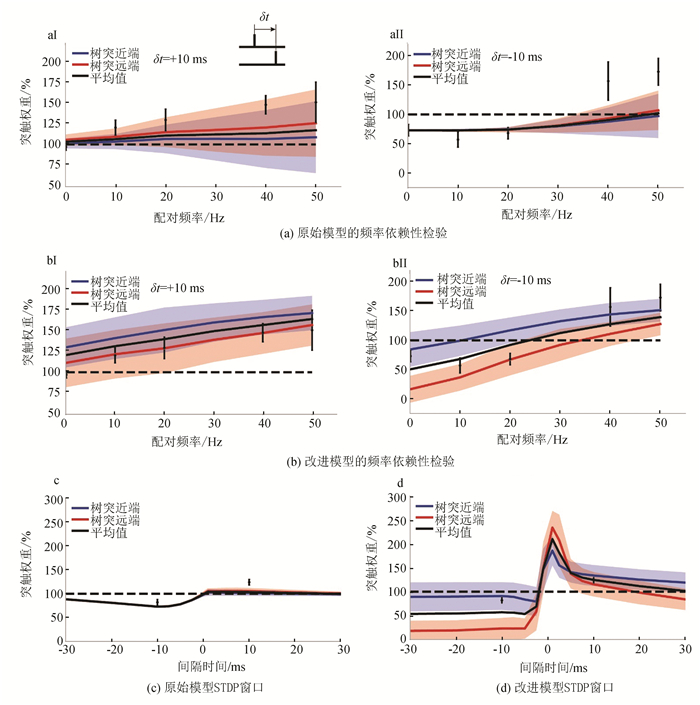
1.3 配对协议为研究脉冲频率依赖可塑性(见图 1bⅠ与1bⅡ),在神经元基底树突的近端与远端分别建立10个突触,初始权重为0.5。前-后配对时,突触前神经元胞体注入3 ms的1 000 pA电流诱导突触前脉冲。静息7 ms后,给突触后神经元注入3 ms的2 000 pA电流诱导突触后脉冲。后-前配对仅调换神经元刺激顺序。配对频率为5~50 Hz,步长5 Hz再加上0.1 Hz。重复5次,权重变化乘以12。研究脉冲时间依赖的可塑性时(见图 1d),在不同的脉冲间隔(1、2.5、5、7.5、10、12.5、15、17.5、20、25和30 ms),重复5次1 Hz的前-后配对或后-前配对。配对协议与Sjöström等人[32]和Wang等人[33]的实验相同,误差范围Wang Huaixing等人的实验[32]。
|
图 1 频率依赖性检验及STDP窗口 Figure 1 Frequency dependence test and STDP window |
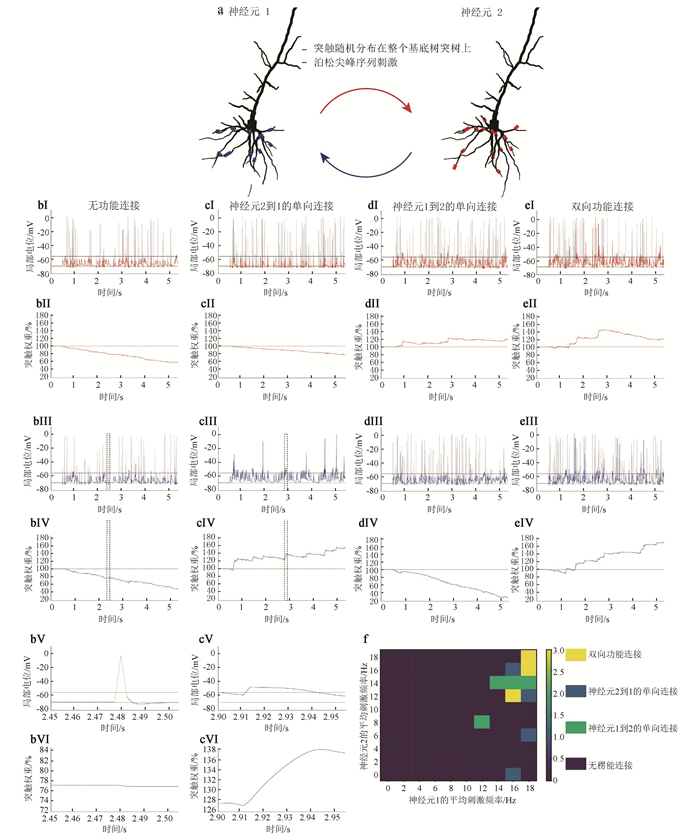
设计5种突触分布方案,研究不同因素如何通过局部电位影响连接模式。方案1研究刺激模式对连接模式的影响。分别在两个神经元基底树突随机选15个隔室建立突触,突触与另一神经元胞体相连(见图 2a),初始权重为0.5。静息500 ms后,通过外部电流注入胞体使两个神经元产生不同平均速率的泊松分布脉冲序列,让它们相互刺激5 s。刺激方案重复10次,每次都随机选取突触位置,记录所有突触电压与权重变化取平均值(见图 2b~e)。主要是观察神经元2的突触后膜局部电位(Ⅰ)与神经元1到2突触权重的变化(Ⅱ),和神经元1突触后膜局部电位(Ⅲ)与神经元2到1突触权重的变化(Ⅳ)。蓝线与红线分别表示神经元1与2的数据。黑色虚线在子图Ⅰ, Ⅲ代表静息电位(-69 mV),在子图Ⅱ, Ⅳ表示初始权重。子图Ⅰ, Ⅲ的黑色实线表示突触权重增强的阈值电位(-55 mV)。图Ⅴ,Ⅵ分别为图Ⅲ与图Ⅳ中虚线框的放大。观察神经元连接模式时,两个神经元的平均刺激频率为0~20 Hz,步长为2 Hz,共55种配对频率。得到无连接、神经元1到2的单向连接、神经元2到1的单向连接以及双向连接的分布。x轴为神经元1的平均刺激频率,y轴为神经元2的平均刺激频率(见图 2f)。
|
图 2 刺激模式对连接模式的影响 Figure 2 Effect of stimulus mode on connection pattern 注:(a)神经元基底树突的随机连接;(b, c, d, e)不同平均刺激频率时神经元电位与突触权重的变化;(f)功能连接模式。 |
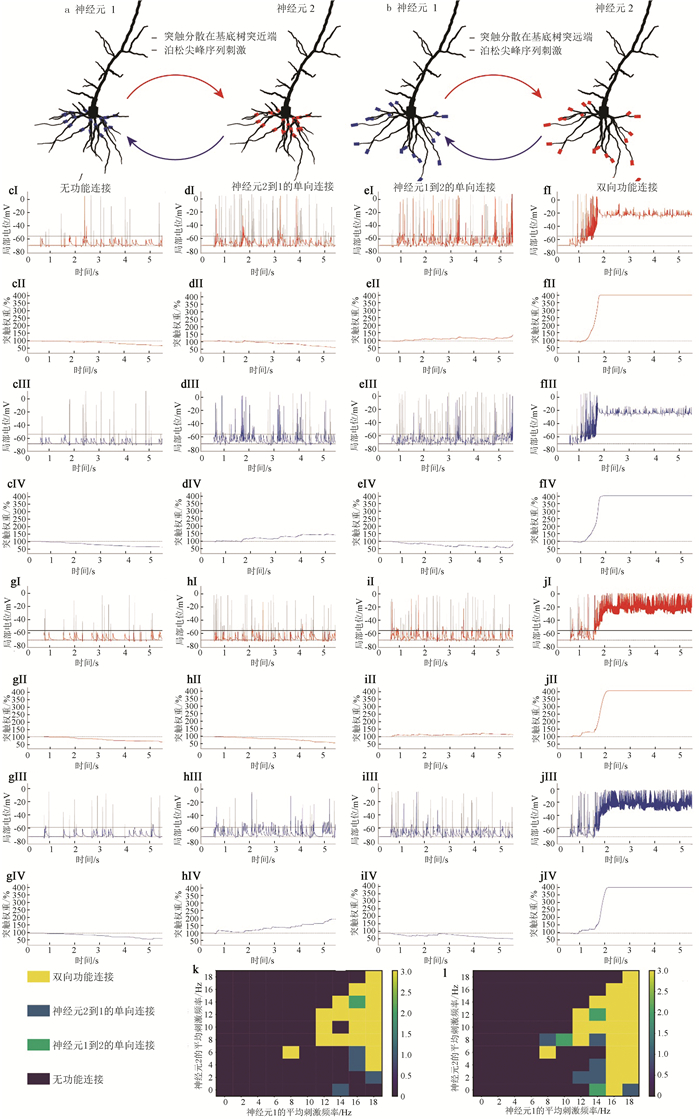
方案2和3研究突触位置对连接模式的影响。方案2中,神经元基底树突近端随机产生21个分散分布的突触,突触与另一神经元胞体相连(见图 3a~b)。方案3则在神经元基底树突远端随机产生19个分散分布突触(见图 4a~b)。因为要分析局部电位与连接模式的变化规律,选取的突触数量要能在0~20 Hz刺激范围内产生四种不同的连接模式,所以不同方案的突触数量不同。方案2和3的刺激方法与方案1相同。
|
图 3 突触位置对连接模式的影响 Figure 3 Effect of synaptic position on connection pattern 注:(a) 神经元基底树突近端的随机连接;(b)神经元基底树突远端的随机连接;(c,d,e,f)近端分布时,不同平均刺激频率下突触电位与突触权重的变化;(g,h,i,j)远端分布时,不同平均刺激频率下突触电位与突触权重的变化;(k)树突近端随机连接的功能连接模式;(l)树突远端随机连接时的功能连接模式。 |
|
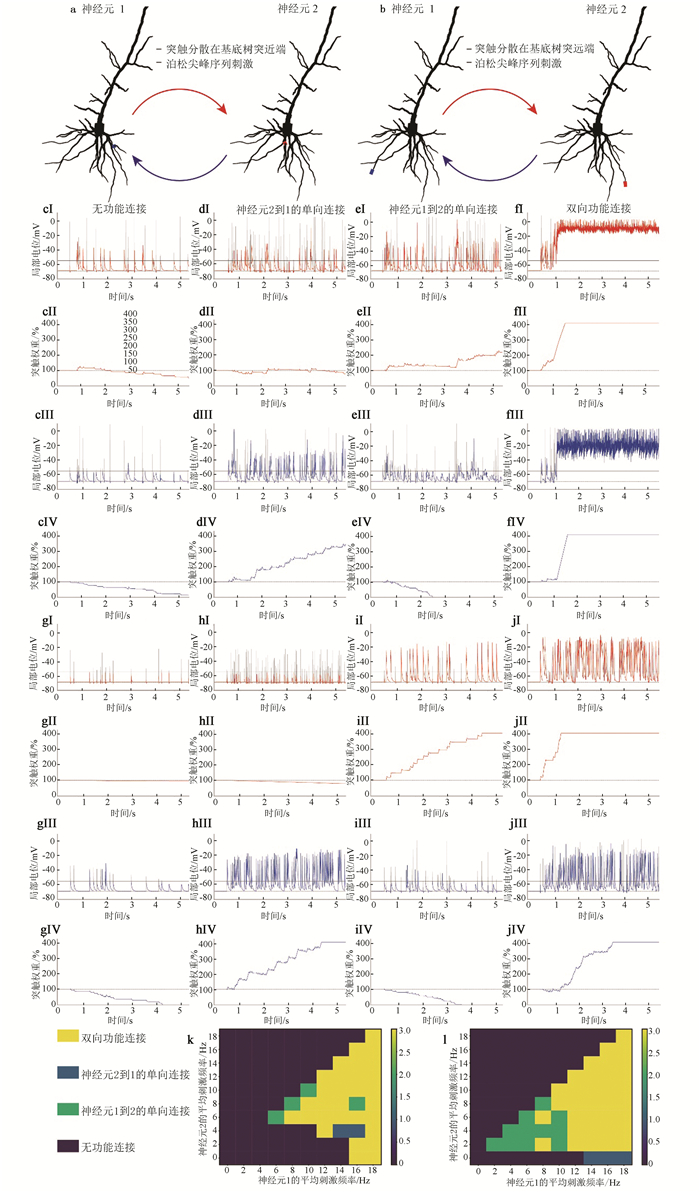
图 4 突触分布对连接模式的影响 Figure 4 Effect of synaptic distribution on connection pattern 注:(a) 神经元基底树突近端突触聚类;(b) 神经元基底树突末梢突触聚类;(c, d, e, f) 近端聚类时,不同平均刺激频率下突触电位与权重的变化;(g, h, i, j) 远端聚类时,不同平均刺激频率下突触电位与权重的变化;(k) 近端连接的最终功能连接模式;(l) 远端连接的最终功能连接模式。 |
方案4和5是方案2和3的延伸,旨在分析突触集群分布时,局部电位与权重的关系是否与分散分布相同。方案4采用15个突触聚集在基底树突近端同一隔室,而方案5采用5个突触集中在基底树突远端同一隔室。刺激方案与方案1相同。
2 结果 2.1 模型的实验检验为证明电压依赖的突触可塑性能反映STDP规则,对改进前后的模型进行频率依赖性检验,刺激间隔时间固定为+10 ms(见图 1aⅠ、1bⅠ)或-10 ms(见图 1aⅡ、1bⅡ),突触位于近端(蓝线)或远端(红线),阴影表示一个标准差,黑色实线表示平均值,虚线代表初始权重。可见改进模型的数据(见图 1b)比Bono与Clopath的可塑性模型[23](见图 1a)更贴合真实值。前-后配对时,突触权重与配对频率正相关,导致LTP(见图 1bⅠ)。后-前配对时,若配对频率低于25 Hz,诱导LTD(见图 1bⅡ)。这可由局部电位解释,前-后配对的突触前脉冲诱导持久的EPSP[8],在此期间突触后神经元的bAP使局部电位超阈值,诱导LTP[34]。后-前配对时,由于bAP持续时间短(1~2 ms)[4],突触前脉冲诱导EPSP之前突触后局部电位已经衰减,所以局部电位为亚阈值,诱导LTD[1, 2]。
再对改进前后的模型进行STDP时间窗口检验(见图 1c-d)。改进模型的STDP窗口在δt>0 ms时(前-后配对),基底树突远端比近端的LTP时间窗口小。而在δt < 0 ms时,远端的LTD时间窗口更宽。这是由于bAP诱导的局部去极化沿树突迅速衰减[9, 12],且无法维持较长时间[4],导致树突远端的bAP与EPSP配对难以产生超阈值电位[7]。
2.2 刺激频率对连接模式的影响两个锥体神经元(见图 2a)平均刺激频率都为10 Hz时,神经元2(红线,见图 2bⅠ)与神经元1(蓝线,见图 2bⅢ)的突触后局部电位都低于阈值-55 mV,对应神经元1到2(见图 2bⅡ)与2到1(见图 2bⅣ)的突触权重分别下降至58.69%与50.35%,两个神经元不产生功能连接。需要说明,突触后局部电位不仅由EPSP组成,还受持续时间短的bAP影响[35](见图 2灰线所示)。将图 2bⅢ与2bⅣ虚线区域放大得到图 2bⅤ与2bⅥ,可见bAP超过阈值-55 mV并达到-3 mV,但持续时间短(5 ms)且随后的亚阈值与超级化电位持续15 ms(幅值为-71.16 mV),突触权重增量为-0.24%。同样将图 2cⅢ与2cⅣ虚线区域放大得到图 2cⅤ与2cⅥ,可见EPSP幅值低(-47.26 mV),但持续时间长(30 ms),突触权重增量为10.58%,因此超阈值小于5 ms时突触权重变化可忽略,将持续时间在5 ms以下的脉冲用灰线表示。下文提及突触电位时,专指红线与蓝线表示的持续时间大于5 ms的电位。
将神经元1与2的平均刺激频率设为16 Hz与0 Hz。此时神经元2局部电位低于阈值而神经元相反(见图 2cⅠ与2cⅢ),对应神经元1到2与2到1的突触权重为77.62%与152.14%(见图 2cⅡ与2cⅣ),产生神经元2到1的单向连接。再将神经元2的刺激频率提升至14 Hz,可见神经元2有三次短暂的超阈值而神经元1反之(见图 2dⅠ与2dⅢ),最终突触权重分别为119.61%与30.15%,(见图 2dⅡ与2dⅣ),产生神经元1到2的单向连接。平均刺激频率都为18 Hz时,神经元1与2都有3至4次的超阈值状态(见图 2eⅠ与2eⅢ),突触权重分别增长至167.22%与119.25%(见图 2eⅡ与2eⅣ),产生双向功能连接。
上述分析指出刺激模式对连接模式的影响能用局部电位解释,刺激诱发突触后局部电位处于超阈值或亚阈值状态,从而改变突触权重,生成四种不同连接模式。使两个神经元的平均刺激频率为0~20 Hz,步长为2 Hz,得到功能连接模式图(见图 2f)。
2.3 突触位置对连接模式的影响突触在树突近端分布时,两个神经元相互在树突近端随机形成21个突触连接(见图 3a)。平均刺激频率都为4 Hz时,神经元突触后电位都为亚阈值(见图 3cⅢ与3cⅠ),对应的突触权重分别下降至69.55%与62.02%(见图 3cⅡ与3cⅣ),不产生连接。当平均刺激频率分别为16 Hz与4 Hz时,神经元2与1的超阈值持续时间分别为17.5 ms与115 ms(见图 3dⅠ与3dⅢ),最终权重为57.99%与142.51%(见图 3dⅡ与3dⅣ),产生稳定的单向连接。提升神经元2的平均刺激频率至14 Hz后,局部电位都在阈值附近震荡(见图 3eⅠ和3eⅢ),突触权重也是如此(141.07%与83.98%,见图 3eⅡ和3eⅣ),产生不稳定单向连接。平均刺激频率为16 Hz时,2 s后局部电位都处于高阈值(见图 3fⅢ与3fⅠ),突触权重达到最大值400.00%(见图 3fⅡ与3fⅣ),产生双向连接。
突触在树突远端分布时,神经元相互在树突末梢随机形成19个突触(见图 3b)。平均刺激频率都为4 Hz时,与近端相同,突触电位都为亚阈值(见图 3gⅠ和3gⅢ),突触权重下降至64.22%和64.95%(见图 3gⅡ和3gⅣ),不形成连接。神经元1的刺激频率提至14 Hz后,仅神经元1在1 s至2 s内超阈值(见图 3hⅢ),也只有神经元2到1突触连接增强(191.33%,见图 3hⅣ),单向连接明显。神经元2的刺激频率调升至12 Hz则情况相反。局部电位都在阈值附近振动(见图 3iⅠ与3iⅢ),突触权重变化不大(112.00%与64.21%,见图 3iⅡ与3iⅣ),产生微弱单向连接。神经元刺激频率都为14 Hz,可见2 s后局部电位维持高阈值(见图 3jⅠ与3jⅢ),突触权重稳定在400.00%(见图 3jⅡ与3jⅣ),产生双向连接。
由上述分析可知突触位置对连接的影响可用局部电位解释。近端与远端突触权重的改变都与突触电位是否超阈值有关,进而影响功能连接。最后将神经元1与2的刺激频率从0 Hz调至20 Hz,得到突触随机分布近端或远端的功能连接模式(见图 3k与3l)。
2.4 突触分布对连接模式的影响突触近端聚类时,神经元胞体在另一神经元随机选择一个树突近端分室形成15个突触连接(见图 4a)。刺激频率都为4 Hz时,与分散分布时相同,突触电位都低于阈值(见图 4cⅠ与4cⅢ),突触权重都持续下降(见图 4cⅡ与4cⅣ),不产生连接。神经元1的刺激频率提升至14 Hz,仅神经元1保持超阈值(见图 4dⅢ),神经元2到1的突触权重上升(335.40%,见图 4dⅣ),产生不稳定单向连接。若将神经元1和2的刺激频率提升至16 Hz与8 Hz,情况相反,仅神经元2维持高阈值(见图 4eⅠ),权重上升至215.76%(见图 4eⅡ),生成单向连接。值得注意的是神经元1局部电位在1~2.8 s处于低阈值,在4 s有175 ms的超阈值(见图 4eⅢ),而神经元2到1的权重在2.8 s后维持0%不变(见图 4eⅣ),这是因为突触权重为0%表示突触消失,此后局部电位不会影响突触权重。神经元刺激频率都为16 Hz时,1.5 s后神经元处于超阈值(见图 4fⅠ与4fⅢ),突触权重升至400.00%(见图 4fⅡ与4fⅣ),产生稳健的双向连接。
突触远端聚类时,神经元胞体在另一神经元随机选择的一个树突远端分室形成5个突触连接(见图 4b)。神经元1与2的刺激频率分别为4 Hz与0 Hz,可见与远端分散分布一致,局部电位都处于亚阈值时(见图 4gⅢ与4gⅠ),突触权重衰减(95.11%与0.02%,见图 4gⅡ与4gⅣ),不产生功能连接。将神经元1的刺激频率提升至16 Hz,仅神经元1超阈值(见图 4hⅢ),产生神经元2到1的单向连接(78.86%与400.00%,见图 4hⅡ与4gⅣ)。若刺激频率都为4 Hz,则仅有神经元2超阈值(见图 4iⅠ),产生神经元1到2的单向连接(400.00%与0.00%,见图 4ill与4ilⅤ)。最后刺激频率都为16 Hz,突触电位都超阈值(见图 4jⅠ和4jⅢ),对应权重都饱和(见图 4jⅡ和4jⅣ),产生双向功能连接。
由此可知,突触分布对连接的影响可用局部电位解释。突触聚类与分散分布都以突触电位决定突触权重变化方向,进而产生四种连接模式。针对突触聚集在树突近端与远端两种情况,使神经元1与2的刺激频率从0 Hz变化至20 Hz,得到连接模式(见图 4k与4l)。
综上所述,突触位置、突触分布与刺激模式对突触权重的影响都可由局部电位解释,所以突触后局部电位是锥体神经元功能连接模式的关键因素。神经元功能连接模式与局部电位的关系是神经元局部电位都处于亚阈值时无连接,单神经元局部电位处于超阈值产生单向连接,两个神经元局部电位都处于超阈值产生双向连接。
3 讨论本研究意义在于,构建出更符合实际的视皮层第5层锥体神经元的可塑性模型。同时,指明突触后局部电位对皮层连接的关键意义,大幅度减少研究皮层连接模式需要考虑的影响因素,降低研究难度。
局部电位对突触权重变化的作用已被多次探讨[5, 9, 11-12]。局部电位能解释动作电位与EPSP配对在树突近端或远端产生LTP/LTD[36-37],也能解释EPSP的幅值随刺激频率增大而增加[8, 38-40]。实验表明皮层突触可塑性的关键在于电压依赖的NMDAR和钙离子通道[41]。Zerlaut与Destexhe提出的神经元模型将树突输入转化为胞体电位,再判断动作电位的产生,可惜不具备突触可塑性[36]。Clopath等人提出的基于电压的STDP模型对实验数据拟合度不高[23],且采用硬边界设计不符合生物实际。局部电位与突触权重的关系难以理清是因为电压受多个离子通道影响,且离子动力学不仅受许多复杂未知因素影响,还受检测方法限制。越来越多理论证明能量是神经活动的统一基础[42-43],也是突触权重变化的基础。根据稳态可塑性,突触权重改变的方向应该是保证神经元总能量维持在稳态[44]。本文从能量角度构造电压依赖的突触可塑性模型,基本原则是脉冲能量状态向静息能量状态趋近。脉冲状态大于静息状态则突触权重减弱,脉冲状态小于静息状态则突触权重增强。由于能量是局部膜电位与膜电流密度的函数,而膜电流密度是膜电位的函数,因此该模型本质上是电压依赖的可塑性模型。
能量模型与实验还可从以下方面进行改进。首先,虽然在一定刺激频率范围内突触具有自平衡能力,但在某些特殊情况,例如突触后膜电流密度持续小于最大膜电流密度时,突触权重会持续增加,因此不得不设置宽松的硬边界。其次,该可塑性模型虽然依赖局部电位,但建模理念源自能量,膜电位与突触权重的直接关系尚不清晰。最后,研究只给出神经元的功能连接模式,但皮层神经元接受数千个突触的输入[38, 45-46],其噪声对突触连接的影响不可忽略[47-49]。此时局部电位与连接模式的关系是否仍遵循少量突触时的关系尚不清楚,这是下一步的研究方向。
4 结论本文从代谢能角度提出一个电压依赖的突触可塑性模型。计算表明突触后膜电位是影响皮层连接模式的关键,突触权重与局部电位有直接联系,神经元局部电位都处于亚阈值时无功能连接,单神经元局部电位超阈值时产生向该神经元的单向连接,两个神经元局部电位都超阈值时产生双向连接。
| [1] |
KAMPA B M, LETZKUS J J, STUART G J. Requirement of dendritic calcium spikes for induction of spike-timing-dependent synaptic plasticity[J]. The Journal of Physiology, 2006, 574(1): 283-290. DOI:10.1113/jphysiol.2006.111062 (  0) 0) |
| [2] |
HARDIE J, SPRUSTON N. Synaptic depolarization is more effective than back-propagating action potentials during induction of associative long-term potentiation in hippocampal pyramidal neurons[J]. The Journal of Neuroscience, 2009, 29(10): 3233-3241. DOI:10.1523/JNEUROSCI.6000-08.2009 (  0) 0) |
| [3] |
GORDON U, POLSKY A, SCHILLER J. Plasticity compartments in basal dendrites of neocortical pyramidal neurons[J]. The Journal of Neuroscience, 2006, 26(49): 12717-12726. DOI:10.1523/JNEUROSCI.3502-06.2006 (  0) 0) |
| [4] |
LISMAN J, SPRUSTON N. Postsynaptic depolarization requirements for LTP and LTD: a critique of spike timing-dependent plasticity[J]. Nature Neuroscience, 2005, 8(7): 839-841. DOI:10.1038/nn0705-839 (  0) 0) |
| [5] |
SANDLER M, SHULMAN Y, SCHILLER J. A novel form of local plasticity in tuft dendrites of neocortical somatosensory layer 5 pyramidal neurons[J]. Neuron, 2016, 90(5): 1028-1042. DOI:10.1016/j.neuron.2016.04.032 (  0) 0) |
| [6] |
CICHON J, GAN W B. Branch-specific dendritic Ca2+ spikes cause persistent synaptic plasticity[J]. Nature, 2015, 520(7546): 180-185. DOI:10.1038/nature14251 (  0) 0) |
| [7] |
LETZKUS J J, KAMPA B M, STUART G J. Learning rules for spike timing-dependent plasticity depend on dendritic synapse location[J]. The Journal of Neuroscience, 2006, 26(41): 10420-10429. DOI:10.1523/JNEUROSCI.2650-06.2006 (  0) 0) |
| [8] |
FROEMKE R C, LETZKUS J J, KAMPA B M, et al. Dendritic synapse location and neocortical spike-timing-dependent plasticity[J]. Frontiers in Synaptic Neuroscience, 2010, 2(29): 1-14. DOI:10.3389/fnsyn.2010.00029 (  0) 0) |
| [9] |
GOLDING N L, STAFF N P, SPRUSTON N. Dendritic spikes as a mechanism for cooperative long-term potentiation[J]. Nature, 2002, 418(6895): 326-331. DOI:10.1038/nature00854 (  0) 0) |
| [10] |
WEBER J P, ANDRÁSFALVY B K, POLITO M, et al. Location-dependent synaptic plasticity rules by dendritic spine cooperativity[J]. Nature Communications, 2016, 7(1): 629-640. DOI:10.1038/ncomms11380 (  0) 0) |
| [11] |
MARKRAM H, LVBKE J, FROTSCHER M, et al. Physiology and anatomy of synaptic connections between thick tufted pyramidal neurons in the developing rat neocortex[J]. The Journal of Physiology, 1997, 500(2): 409-440. DOI:10.1113/jphysiol.1997.sp022031 (  0) 0) |
| [12] |
NICHOLSON D A, TRANA R, KATZ Y, et al. Distance-dependent differences in synapse number and AMPA receptor expression in hippocampal CA1 pyramidal neurons[J]. Neuron, 2006, 50(3): 431-442. DOI:10.1016/j.neuron.2006.03.022 (  0) 0) |
| [13] |
KUMAR A, MEHTA M R. Frequency dependent changes in NMDAR-dependent synaptic plasticity[J]. Frontiers in Computational Neuroscience, 2011, 5(38): 1-10. DOI:10.3389/fncom.2011.00038 (  0) 0) |
| [14] |
SHOUVAL H Z, WANG S S H, WITTENBERG G M. Spike timing dependent plasticity: a consequence of more fundamental learning rules[J]. Frontiers in Computational Neuroscience, 2010, 4(19): 1-13. DOI:10.3389/fncom.2010.00019 (  0) 0) |
| [15] |
KECK T, TOYOIZUMI T, CHEN L, et al. Integrating Hebbian and homeostatic plasticity: the current state of the field and future research directions[J]. Philosophical Transactions of The Royal Society B: Biological Sciences, 2017, 372(1715): 20160158. DOI:10.1098/rstb.2016.0158 (  0) 0) |
| [16] |
LITWIN-KUMAR A, DOIRON B. Formation and maintenance of neuronal assemblies through synaptic plasticity[J]. Nature Communications, 2014, 5(1): 1868-1871. DOI:10.1038/ncomms6319 (  0) 0) |
| [17] |
ZENKE F, AGNES E J, GERSTNER W. Diverse synaptic plasticity mechanisms orchestrated to form and retrieve memories in spiking neural networks[J]. Nature Communications, 2015, 6(1): 4-375. DOI:10.1038/ncomms7922 (  0) 0) |
| [18] |
CHISTIAKOVA M, BANNON N M, CHEN J Y, et al. Homeostatic role of heterosynaptic plasticity: models and experiments[J]. Frontiers in Computational Neuroscience, 2015, 9(89): 1-10. DOI:10.3389/fncom.2015.00089 (  0) 0) |
| [19] |
MANNINEN T, HITURI K, KOTALESKI J H, et al. Postsynaptic signal transduction models for long-term potentiation and depression[J]. Frontiers in Computational Neuroscience, 2010, 4(152): 1-10. DOI:10.3389/fncom.2010.00152 (  0) 0) |
| [20] |
BIENENSTOCK E L, COOPER L N, MUNRO P W. Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex[J]. The Journal of Neuroscience, 1982, 2(1): 32-48. DOI:10.1097/00005072-198211000-00009 (  0) 0) |
| [21] |
CLOPATH C, LARS B, VASILAKI E, et al. Connectivity reflects coding: a model of voltage-based spike-timing-dependent-plasticity with homeostasis[J]. Nature Neurosciences, 2010, 13(3): 344-352. DOI:10.1038/nn.2479 (  0) 0) |
| [22] |
CARLSON K D, RICHERT M, DUTT N, et al. Biologically plausible models of homeostasis and STDP: stability and learning in spiking neural networks[EB/OL]. https://doi.org/10.1109/IJCNN.2013.6706961, 2013. DOI: 10.1109/IJCNN.2013.6706961.
(  0) 0) |
| [23] |
BONO J, COLPATH C. Modeling somatic and dendritic spike mediated plasticity at the single neuron and network level[J]. Nature Communications, 2017, 8(1): 307-319. DOI:10.1038/s41467-017-00740-z (  0) 0) |
| [24] |
GOODMAN D, BRETTE R. The brian simulator[J]. Frontiers in Neuroscience, 2009, 3(2): 192-197. DOI:10.3389/neuro.01.026.2009 (  0) 0) |
| [25] |
DESTEXHE A, RUDOLPH M, PARÉ D. The high-conductance state of neocortical neurons in vivo[J]. Nature Reviews Neuroscience, 2003, 4(9): 739-751. DOI:10.1038/nrn1198 (  0) 0) |
| [26] |
Meyer J F, GOLSHANI P, SMIRNAKIS S M. The effect of single pyramidal neuron firing within layer 2/3 and layer 4 in mouse V1[J]. Frontiers in Neural Circuits, 2018, 12(29): 1-14. DOI:10.3389/fncir.2018.00029 (  0) 0) |
| [27] |
HOUWELING A R, BRECHT M. Behavioural report of single neuron stimulation in somatosensory cortex[J]. e-Neuroforum, 2008, 14(1): 174-176. DOI:10.1515/nf-2008-0105 (  0) 0) |
| [28] |
KUFFLER S W, NICHOLLS J G. From neuron to brain[J]. Quarterly Review of Biology, 1976, 94(1): 303-322. DOI:10.1016/S0928-4257(00)01090-1 (  0) 0) |
| [29] |
DEBANNE D, INGLEBERT Y, RUSSIER M. Plasticity of intrinsic neuronal excitability[J]. Current Opinion in Neurobiology, 2018, 54: 73-82. DOI:10.1016/j.conb.2018.09.001 (  0) 0) |
| [30] |
GASSELIN G, INGLEBERT Y, ANKRI N, et al. Plasticity of intrinsic excitability during LTD is mediated by bidirectional changes in h-channel activity[J]. Scientific Reports, 2017, 7(1): 21-32. DOI:10.1038/s41598-017-14874-z (  0) 0) |
| [31] |
CAMPANAC E, DAOUDAL G, ANKRI N, et al. Downregulation of dendritic I(h) in CA1 pyramidal neurons after LTP[J]. Journal of Neuroscience, 2008, 28(34): 8635-8643. DOI:10.1523/JNEUROSCI.1411-08.2008 (  0) 0) |
| [32] |
SJÖSTRÖM P J, TURRIGIANO G G, NELSON S B. Rate, timing, and cooperativity jointly determine cortical synaptic plasticity[J]. Neuron, 2001, 32(6): 1149-1164. DOI:10.1016/S0896-6273(01)00542-6 (  0) 0) |
| [33] |
WANG H X, GERKIN R C, NAUEN D W, et al. Coactivation and timing-dependent integration of synaptic potentiation and depression[J]. Nature Neuroscience, 2005, 8(2): 187-193. DOI:10.1038/nn1387 (  0) 0) |
| [34] |
SHOUVAL H Z, BEAR M F, COOPER L N. A unified model of NMDA receptor-dependent bidirectional synaptic plasticity[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(16): 10831-10836. DOI:10.1073/pnas.152343099 (  0) 0) |
| [35] |
LARKUM M E, NEVIAN T. Synaptic clustering by dendritic signaling mechanisms[J]. Current Opinion in Neurobiology, 2008, 18(3): 321-331. DOI:10.1016/j.conb.2008.08.013 (  0) 0) |
| [36] |
ZERLAUT Y, DESTEXHE A. Heterogeneous firing responses predict diverse couplings to presynaptic activity in mice layer V pyramidal neurons[J]. PLoS Computational Biology, 2017, 13(4): e1005452. DOI:10.1371/journal.pcbi.1005452 (  0) 0) |
| [37] |
LETZKUS J J, KAMPA B M, STUART G J. Learning rules for spike timing-dependent plasticity depend on dendritic synapse location[J]. Journal of Neuroscience, 2006, 26(41): 10420-10429. DOI:10.1523/JNEUROSCI.2650-06.2006 (  0) 0) |
| [38] |
RANJBAR-SLAMLOO Y, ARABZADEH E. High-velocity stimulation evokes "dense" population response in layer 2/3 vibrissal cortex[J]. Journal of Neurophysiology, 2017, 117(3): 1218-1228. DOI:10.1152/jn.00815.2016 (  0) 0) |
| [39] |
LEE S, MEYER J F, PARK J, et al. Visually driven neuropil activity and information encoding in mouse primary visual cortex[J]. Frontiers in Neural Circuits, 2017, 11(1): 1-18. DOI:10.3389/fncir.2017.00050 (  0) 0) |
| [40] |
LINARO D, OCKER G K, DOIRON B, et al. Correlation transfer by layer 5 cortical neurons under recreated synaptic inputs in vitro[J]. The Journal of Neuroscience, 2019, 39(39): 3169-3118. DOI:10.1523/JNEUROSCI.3169-18.2019 (  0) 0) |
| [41] |
GRAUPNER M, BRUNEL N. Calcium-based plasticity model explains sensitivity of synaptic changes to spike pattern, rate, and dendritic location[J]. Proceedings of the National Academy of Sciences, 2012, 109(10): 3991-3996. DOI:10.1073/pnas.1109359109 (  0) 0) |
| [42] |
YU L, YU Y. Energy-efficient neural information processing in individual neurons and neuronal networks[J]. Journal of Neuroscience Research, 2017, 95(11): 2253-2266. DOI:10.1002/jnr.24131 (  0) 0) |
| [43] |
HASENSTAUB A, OTTE S, CALLAWAY E, et al. Metabolic cost as a unifying principle governing neuronal biophysics[J]. Proceedings of the National Academy of Sciences of the United States of America, 2010, 107(27): 12329-12334. DOI:10.1073/pnas.0914886107 (  0) 0) |
| [44] |
TURRIGIANO G. Homeostatic synaptic plasticity: local and global mechanisms for stabilizing neuronal function[J]. Cold Spring Harbor Perspectives in Biology, 2012, 4(1): a005736. DOI:10.1101/cshperspect.a005736 (  0) 0) |
| [45] |
ANTON-SANCHEZ L, LARRAÑAGA P, BENAVIDES-PICCIONE R, et al. Three-dimensional spatial modeling of spines along dendritic networks in human cortical pyramidal neurons[J]. PloS One, 2017, 12(6): e0180400. DOI:10.1371/journal.pone.0180400 (  0) 0) |
| [46] |
WILSON C J. Predicting the response of striatal spiny neurons to sinusoidal input[J]. Journal of Neurophysiology, 2017, 118(2): 855-873. DOI:10.1152/jn.00143.2017 (  0) 0) |
| [47] |
ZERLAUT Y, DESTEXHE A. Enhanced responsiveness and low-level awareness in stochastic network states[J]. Neuron, 2017, 94(5): 1002-1009. DOI:10.1016/j.neuron.2017.04.001 (  0) 0) |
| [48] |
KOREN V, DENÈVE S. Computational account of spontaneous activity as a signature of predictive coding[J]. PLOS Computational Biology, 2017, 13(1): e1005355. DOI:10.1371/journal.pcbi.1005355 (  0) 0) |
| [49] |
DOOSE J, DORON G, BRECHT M, et al. Noisy juxtacellular stimulation in vivo leads to reliable spiking and reveals high-frequency coding in single neurons[J]. The Journal of Neuroscience, 2016, 36(43): 11120-11132. DOI:10.1523/JNEUROSCI.0787-16.2016 (  0) 0) |
 2021, Vol. 19
2021, Vol. 19


