蛋白质是生命过程中的重要有机物,其序列、结构和功能多种多样。蛋白质由20种氨基酸通过肽键结合形成肽链,这些肽链通过折叠形成多种多样的结构[1]。蛋白质的序列决定结构,而序列和结构又决定了它的功能[1]。研究蛋白质的结构分类和预测对深入了解蛋白质的作用和功能具有重要意义。蛋白质结构的研究分为蛋白质二级结构的研究和对其空间结构的研究,其中蛋白质的二级结构指的是其骨干肽链的结构。蛋白质的二级结构可以分为不同的结构类型。例如,在CATH数据库中,蛋白质的二级结构分为三个主要结构类型:主要α结构(Mainly α structures)类,主要β结构(Mainly β structures)类,和混合α与β结构(Mixed α and β structures)类[1]。蛋白质二级结构的预测通常利用蛋白质的氨基酸序列信息预测其可能形成的二级结构类型。常用的蛋白质二级结构预测方法包括人工神经网络法、最近邻法和支持向量机法等[1]。一些经典的蛋白质二级结构预测方法包括Chou- Fasman[2]、GOR[3]、PHD[4]、CONCORD[5]、I-TASSER[6], 以及Robetta[7]等方法。
蛋白质的二级结构可以进一步分为不同的折叠结构。Ding和Dubchak提出了一种基于支持向量机和神经网络的多类蛋白质折叠识别方法[8]。Edler和Grassmann做出了关于统计学方法在蛋白质折叠类预测中的角色和结果的研究[9]。Huang等提出了一种基于分层学习体系结构的带自动特征选择的蛋白质折叠分类方法[10]。Jo等做出了利用深度学习网络来改进蛋白质折叠识别的研究[11]。Khan和Shahzad提出了一种新的受蚂蚁启发的基于关联规则分类器的蛋白质分类方法[12]。Markowetz、Edler和Vingron做出了一项基于支持向量机的关于蛋白质折叠类预测的研究[13]。Tan, Gilbert和Deville提出了一种基于新的集成机器学习方法的多类蛋白质折叠分类方法[14]。Wei等提出了一种基于新特征提取技术的增强的蛋白质折叠识别方法[15]。Wei和Zou总结了关于基于机器学习的蛋白质折叠识别方法研究进展综述[16]。
蛋白质的二级结构也可以通过氨基酸的物理、化学性质来进行分类。Rackovsky在文献[17]中提出利用氨基酸的物理属性对蛋白质二级结构类型进行分类的研究。该研究利用10种主要的氨基酸物理属性将CATH数据按三种主要结构类型(主要α类、主要β类、混合α和β结构类)进行分类。该研究表明蛋白质的结构与氨基酸的物理属性具有一定的联系[17]。
蛋白质序列的特征提取对研究蛋白质的结构具有重要应用[18]。自然向量通过计算氨基酸的成分和排序将蛋白质序列映射成60维实空间中的向量,每一个序列的自然向量与该序列是一一对应的[18]。由自然向量法可以导出一系列其它的序列特征提取方法[19],如:K-串字典法[20]、蛋白质映射[21-22]等。这些特征提取法可用于提取蛋白质的序列特征,进而用于对其结构的分类和预测。
利用5-mer中间氨基酸的扭转角统计偏好来对蛋白质序列进行结构类型的预测和分类是一种新的蛋白质二级结构分类方法。该方法从PDB数据库中获取5-mer的统计信息,并通过对5-mer中间氨基酸扭转角的统计和聚类,经过组合、打分、筛选和拼接实现对蛋白质序列的结构类型预测,即将蛋白质序列按CATH的分类分为三种主要结构类型:主要α结构类、主要β结构类,混合α和β结构类。该新方法源于I-TASSER和Robetta这两种服务器式预测方法,与I-TASSER和Robetta的主要区别在于,新方法基于局部序列环境对扭转角偏好的影响,即通过统计局部序列单元即5-mer的扭转角偏好,实现蛋白质二级结构类型的预测,而I-TASSER与Robetta则是通过同源模板的匹配来进行结构预测和分类。
在研究方法中,详细介绍该新方法的实现过程和步骤,并提供方法实现的流程图。在结果中,展示5-mer的统计分析结果,以及两组随机抽取的CATH数据的结构分类结果,所有分类结果均与四种基于序列特征的结构预测或分类方法进行比较,这四种方法分别为:(1)基于平均属性因子和自然向量特征提取的最小平方误差(MSE)超平面[2]分类方法;(2)PseAAC的支持向量机分类方法;(3)Chou-Fasman方法。在讨论部分,详细总结和讨论了新方法的特点和有效性。
1 研究方法分步介绍5-mer扭转角分类方法的实现步骤。主要分为两部分:(1)PDB数据库中5-mer中间氨基酸扭转角结构偏好的统计分析;(2)利用5-mer中间氨基酸结构统计偏好对蛋白质序列的结构类型进行预测。
1.1 5-mer扭转角的统计分析与聚类 1.1.1 5-mer中间氨基酸扭转角的统计分析首先统计PDB数据库中5-mer中间氨基酸的扭转角结构类型。从PDB数据库中提取氨基酸扭转角的统计信息。PDB数据库中包含超过100 000条X-Ray实验获取的PDB结构,通过数据库中的这些PDB结构信息来获取5-mer的统计信息。所谓5-mer即是由5个相邻氨基酸组成的长度为5的局部序列。对5-mer进行统计分析不仅可以获取充足的统计数据,而且5-mer是能体现局部结构的最小序列单元。在文献[23]中, Morikawa提出长度为5的氨基酸序列可用于表示蛋白质序列的局部结构分布。一方面,长度为5的局部序列已经能够充分表示蛋白质的局部结构倾向,更短的序列无法充分表达局部序列对结构的影响。另一方面,表达局部结构的氨基酸序列不应过长,过长的序列会导致无法获取足够数量的统计数据。长度为5的局部序列既保证了充足数量的统计数据,又能够体现局部序列对结构的影响。
给定一条长度为L的氨基酸序列a1a2…aL,该序列中共含有L-4个5-mer: ai-2ai-1aiai+1ai+2, 3≤i≤L-3。为了预测这条氨基酸序列的结构类型, 统计PDB数据库中通过X-Ray实验获得的PDB结构中5-mer中间氨基酸的扭转角信息,并通过聚类获取5-mer中间氨基酸扭转角的统计偏好。
1.1.2 拉氏图中扭转角的聚类分析从PDB数据库中获取所有可能出现的5-mer序列,以及其出现频数和中间氨基酸的(φ, ψ) 扭转角列表。每一种5-mer都对应一个记录其中间氨基酸扭转角值的列表,通过对列表中扭转角值的聚类分析来获取5-mer中间氨基酸扭转角的结构偏好。
将每一种5-mer扭转角列表中的(φ, ψ)值画在同一张拉氏图中,图中所有的(φ, ψ)点都落在[-180, 180]×[-180, 180]区域内。使用下列方法来获取每种5-mer中间氨基酸扭转角的聚类。
首先,在拉氏图中[-180, 180]×[-180, 180]区域内的整坐标点上定义浓度:
| $ {d_r}\left( {\varphi , \psi } \right) = \frac{{{N_r}\left( {\varphi , \psi } \right)}}{N}, $ | (1) |
其中Nr(φ, ψ)表示该拉氏图中落入圆心为(φ, ψ)半径为r的闭圆域内的扭转角个数,N表示整个拉氏图中总的扭转角点数,即5-mer扭转角列表中的(φ, ψ)扭转角个数,也即该5-mer在PDB数据库中出现的次数。该浓度值即为给定5-mer的扭转角列表中落入整坐标点(φ, ψ)的闭圆域内的扭转角比例。计算拉氏图中[-180, 180]×[-180, 180]区域内361x361个整坐标点对应的浓度值。扭转角的聚类即为拉氏图中扭转角的局部聚集区域。将拉氏图中局部浓度峰值所在坐标定义为聚类的中心。
为了研究圆域半径r对浓度的影响,将r从1到20进行遍历并计算相应的浓度值。给出了一个在不同圆域半径下进行聚类分析的例子(见图 1),当r较小时,聚类较为离散;而当r增大时,聚类的分布变得较为平坦。通过比较发现,不同圆域半径对应的聚类相似。发现r=10左右为识别聚类的理想值。为了避免圆域半径对聚类的影响,对r从1到20变化时计算得到的扭转角聚类中心取平均作为最终的聚类中心,该聚类中心代表了相应5-mer中间氨基酸扭转角的统计偏好。

|
图 1 不同浓度半径下的聚类情况 Figure 1 Clustering situations with different density radius |
图 1显示了浓度半径r=1, 3, 5, 10, 15, 20对应的扭转角聚类情况。以5-mer ‘NLYFQ’为例计算不同浓度半径下的聚类情况。可以看出不同半径对应的聚类位置不变,而聚类随着半径的增加变得更加平坦。用Ω表示PDB数据库中所有5-mer的集合。记S为Ω中的一个5-mer,其中间氨基酸扭转角的聚类个数为MS,用Ci(s)表示S中间氨基酸扭转角的聚类中心(i=1, …, Ms)。5-mer中间氨基酸扭转角的聚类反映了在该5-mer:ai-2ai-1aiai+1ai+2序列环境下,中间氨基酸ai的扭转角取值倾向。用上述浓度分析5-mer集合Ω中每一个5-mer中间氨基酸的扭转角聚类情况。
1.2 蛋白质序列结构类型的预测利用已经获取Ω中所有5-mer中间氨基酸的扭转角聚类来实现蛋白质序列的结构类型预测。整个预测过程分为三个阶段:(1)分段与聚类,(2)打分和分组,(3)拼接与筛选。
1.2.1 序列分段与扭转角的聚类(1) 序列分段设 a1a2…aL是一条长度为L的氨基酸序列。在该序列中,除了开头两个和结尾两个氨基酸外,每个氨基酸都可以看成序列中某个5-mer的中间氨基酸。例如,a3是5-mer:a1a2a3a4a5的中间氨基酸。一般情况下,ai是5-mer:ai-2ai-1aiai+1ai+2的中间氨基酸,3≤i≤L-2。
由于利用5-mer中间氨基酸的扭转角统计偏好来预测蛋白质序列的结构类型,因此对于序列a1a2…aL来说,实际上预测的是子序列a3a4…aL-3aL-2的结构类型。开头和结尾各两个氨基酸作为第一个和最后一个5-mer的背景氨基酸。将a3a4…aL-3aL-2分成首尾相接的5-mer序列段: a3a4a5a6a7, a8a9a10a11a12, …, a5i-2a5i-1a5ia5i+1a5i+2, …, 最后一个序列段可能长度不足5,因此不一定是一个完整的5-mer。
(2) 聚类分析 对每条序列段Si: a5i-2a5i-1a5ia5i+1a5i+2,
(
| 表 1 序列段Si对应的5-mer中间氨基酸扭转角聚类中心 Table 1 Torsion angle cluster centers for the middle amino acids of 5-mers in sequence segment Si |
表中显示了序列段Si: a5i-2a5i-1a5ia5i+1a5i+2, (
由于每个5-mer的中间氨基酸都对应若干聚类,因此序列段Si: a5i-2a5i-1a5ia5i+1a5i+2(
(1) 打分策略 在序列段Si: a5i-2a5i-1a5ia5i+1a5i+2的Mi种聚类组合中,每一种聚类组合可以表示为:
| $ \begin{array}{l} {p_{{k_1}{k_2}{k_3}{k_4}{k_5}}}\left( {{S_i}} \right) = {C_{{k_{_1}}}}\left( {{s_{i,1}}} \right){C_{{k_2}}}\left( {{s_{i,2}}} \right){C_{{k_3}}}\left( {{s_{i,3}}} \right){\rm{ }}\\ {C_{{k_4}}}\left( {{s_{i,4}}} \right){C_{{k_5}}}({s_{i,5}}), \end{array} $ | (2) |
其中1≤kj≤Msi, j为第j个(j=1, 2, 3, 4, 5)氨基酸的聚类索引,Msi, j为第j个氨基酸的聚类总个数,Ckj(si, j)∈{Ck(si, j)|k=1, …, Msi, j} 表示每个5-mer si, j中间氨基酸的扭转角聚类中心。定义阈值T>0和一个1×4维距离向量dk1k2k3k4k5(Si)=(d1, d2, d3, d4), 其中dj表示聚类中心Ckj(si, j)和Ckj+1(si, j+1) 之间的欧氏距离, 即dj=|Ckj(si, j)-Ckj+1(si, j+1)|, j=1, 2, 3, 4。利用阈值T来过滤距离向量dk1k2k3k4k5(Si)=(d1, d2, d3, d4), 并获得一个逻辑值向量bk1k2k3k4k5(Si)=(b1, b2, b3, b4) 其中逻辑值bj定义如下:
| $ {b_j} = \left\{ \begin{array}{l} 1, {\rm{if}}\;{d_j} \le T\\ 0, {\rm{if}}\;{d_j} > T' \end{array} \right.\;\;\;j = 1, 2, 3, 4. $ | (3) |
给定聚类组合
统计逻辑值向量
| $ {\mathit{\Omega }_{{k_1}{k_2}{k_3}{k_4}{k_5}}}\left( {{S_i}} \right) = \sum\limits_{k = 1}^{{n_i}} {{e^{{l_k}}}} $ | (4) |
其中kj=1, 2, …, Msi, j (j=1, 2, 3, 4, 5) 表示序列段Si中第j个氨基酸对应5-mer的聚类索引, ni表示这个聚类组合逻辑值向量中1串的个数, lk(k=1, 2, …, ni)表示逻辑值向量中第k个1串的长度。
(2)分组 按上述方法计算序列段Si中每一种聚类组合pk1k2k3k4k5(Si)的分值Ωk1k2k3k4k5(Si),并通过下述方法将其分为不同的结构类型。对序列段Si的任意一个聚类组合pk1k2k3k4k5(Si),定义为:
| $ {{\bar p}_{{k_1}{k_2}{k_3}{k_4}{k_5}}}\left( {{S_i}} \right) = \left( {{{\bar \varphi }_{{k_1}{k_2}{k_3}{k_4}{k_5}}}, {{\bar \psi }_{{k_1}{k_2}{k_3}{k_4}{k_5}}}} \right), $ | (5) |
为该聚类组合的扭转角平均值,其中φk1k2k3k4k5和ψk1k2k3k4k5分别为聚类中心: Ck1(si, 1)Ck2(si, 2)
Ck3(si, 3)Ck4(si, 4)Ck5(si, 5)的φ和ψ角平均值。为序列段Si中所有Mi种聚类组合计算(φ, ψ)角平均值pk1k2k3k4k5(Si),并通过前面所述浓度法对Mi种聚类组合的扭转角平均值pk1k2k3k4k5(Si)进行聚类,将获得的聚类按扭转角对应的区域分为若干结构类型Gk(Si), 其中
将每个结构类
| $ {\mathit{\Omega }_{{{k'}_1}{{k'}_2}{{k'}_3}{{k'}_4}{{k'}_5}}}\left( {{S_i}} \right) = {\max _{\overline p {{k'}_1}{{k'}_2}{{k'}_3}{{k'}_4}{{k'}_5}\left( {{S_i}} \right) \in {G_k}\left( {{S_i}} \right)}}\left\{ {{\mathit{\Omega }_{{k_1}{k_2}{k_3}{k_4}{k_5}}}\left( {{S_i}} \right)} \right\}, $ | (6) |
时,选择聚类组合
| $ \begin{array}{l} P\left( {{S_i}} \right) = \left\{ {{p_{{{k'}_1}{{k'}_2}{{k'}_3}{{k'}_4}{{k'}_5}}}\left( {{S_i}} \right)\left| {{\mathit{\Omega }_{{{k'}_1}{{k'}_2}{{k'}_3}{{k'}_4}{{k'}_5}}}\left( {{S_i}} \right) = } \right.} \right.\\ \left. {\mathop {\max }\limits_{\overline p {{k'}_1}{{k'}_2}{{k'}_3}{{k'}_4}{{k'}_5}\left( {{S_i}} \right) \in {G_k}\left( {{S_i}} \right)} \left\{ {{\mathit{\Omega }_{{k_1}{k_2}{k_3}{k_4}{k_5}}}\left( {{S_i}} \right)} \right\}} \right\}. \end{array} $ | (7) |
其中Si是上文中所研究的5-mer序列段,
(3) 结构的拼接与筛选 在序列分段阶段,整条蛋白质序列被分为
在拼接与筛选阶段,使用一个迭代的拼接策略。从第一个序列段S1开始, 将序列段S1与S2的结构拼接在一起形成序列段S1S2的结构。记NP(Si)为序列段Si的预测结构数,则序列段S1与S2拼接后的预测结构数为NP(S1)·NP(S2)。
将列段S1S2的所有Np(S1)·Np(S2)个预测结构的扭转角聚类组合记为集合{p(S1S2)}。为序列段S1S2相邻扭转角聚类中心计算一个1×9维的距离向量
| $ \mathit{\Omega }\left( {{S_1}{S_2}} \right) = \sum\limits_{k = 1}^n {{e^{{l_k}}}} $ | (8) |
其中n表示逻辑值向量中1-串的个数, lk表示每个1串的长度。为所有NP(S1)·NP(S2)种结构组合计算分值,获得一个相应于集合{p(S1S2)}的结构组合打分列表{Ω(S1S2)}。从打分列表中选取分值最高的5个结构为序列段S1S2的预测结构。
在第i个迭代循环中,获得序列段S1S2…Si的5个最优预测结构{p(S1S2…Si)}。接下来,将序列段S1S2…Si与Si+1进行拼接。类似于上述步骤,总共获得Np(S1S2…Si)·Np(Si+1)种组合结构{p(S1S2…Si+1)}。通过计算相邻氨基酸扭转角聚类中心的距离向量d(S1S2…Si+1)=(d1, d2, …, d5*(i+1)-1)和逻辑值向量b(S1S2…Si+1)=(b1, b2, …, b5*(i+1)-1)来为拼接结构进行打分。对所有的结构组合{p(S1S2…Si+1)}计算打分列表{Ω(S1S2…Si+1)},并选取其中分值最高的5个拼接结构作为序列段S1S2…Si+1的预测结构。
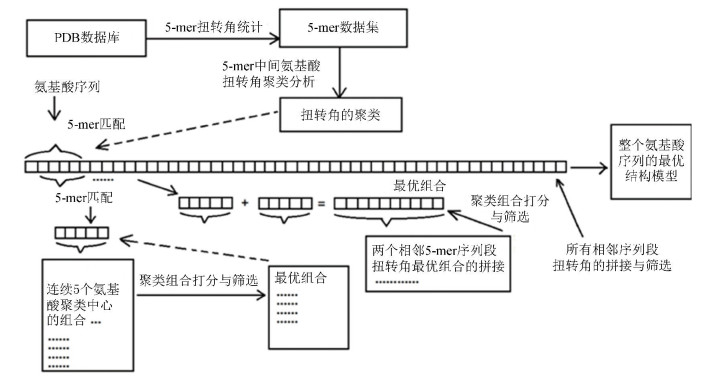
迭代过程一直到所有序列段都拼接起来为止。最后,从整条序列的打分列表中选取分值最高的5个结构作为最终的预测结构。预测方法的流程图(见图 2)。
|
图 2 5-mer扭转角结构预测法流程图 Figure 2 Flow chart for the structural prediction method based on torsion angle of 5-mers |
图 2显示了5-mer扭转角结构预测方法的流程图。流程图主要分为两部分: (1)5-mer扭转角的统计与聚类分析; (2)氨基酸扭转角聚类的组合、拼接与筛选。
(4) 结构的分类与准确率 通过上述步骤,每一条蛋白质序列得到5个最优(分值最高)预测结构,利用这5个最优结构来判断蛋白质的结构类型。对于每个预测结构来说,它的结构类型取决于该结构中不同结构类型扭转角的统计频率。在拉氏图中,α螺旋和β平面这两种不同结构的(φ, ψ)扭转角位于拉氏图中的不同区域[25-29]。α螺旋对应的扭转角集中于(-60°, -45°)附近的区域内[25-29]。更一般地, 在α螺旋结构中,一个氨基酸残基的ψ角和下一个氨基酸残基的φ角之和大致接近于-105°[25-29]。因此,α螺旋的扭转角在拉氏图中一般散布于由(-90°, -15°) 到(-35°, -70°)的对角线(斜率为-1)区域内[25-29]。α螺旋既有右手α螺旋,也有左手α螺旋,其中最普遍的为右手α螺旋。左手α螺旋的扭转角在拉氏图中分布于与右手α螺旋关于原点对称的区域。将右手和左手α螺旋统称为α螺旋,并将落在左手或右手α螺旋区域及附近的扭转角通称为α类扭转角。
β平面的扭转角通常落在(-135°, 135°) 附近的区域内(大致来说,在拉氏图的左上角区域),并且明显偏离构象(-180°, 180°) [26-29]。在平行β平面中,扭转角接近于(-120°, 115°), 而在反平行β平面中(φ, ψ)扭转角接近于(-140°, 135°)。考虑平行和反平行的β平面,并将两种β平面结构统称为β平面,落在β平面扭转角区域及附近的扭转角通称为β类扭转角[27-30]。落在α类和β类扭转角区域外的扭转角则被分为第三类,该类扭转角对应于无规则的“环”[31]。
统计每个最优结构中上述三种类型扭转角出现的频率。若α类扭转角频率最高且α类扭转角频率明显高于其它类扭转角时,认为该预测结构为主要α结构类(C=1);若β类扭转角的频率最高且β类扭转角的频率明显高于其它类扭转角时,该预测结构被认为属于主要β结构类(C=2);若不满足前两种情况,则认为该预测结构为α与β的混合类(C=3)。
统计数据集中每种结构类型下获得正确分类的蛋白质序列数并记为vi,角标i=1, 2, 3分别对应CATH的三种主要结构类型。我们将该频数除以数据集中该结构类下真实的蛋白质序列数Ni,得到该结构类型的分类正确率为:
| $ {A_i} = \frac{{{\upsilon _i}}}{{{N_i}}}, i = 1, 2, 3. $ | (9) |
分析和总结PDB数据库中5-mer中间氨基酸的扭转角统计偏好,并利用两组随机抽取的CATH数据来验证新方法的有效性。
2.1 5-mer扭转角的偏好统计统计PDB数据库中蛋白质序列的5-mer及其中间氨基酸的扭转角列表,并对得到的5-mer扭转角列表进行聚类分析。在聚类分析中,使用不同的圆域半径来计算扭转角的聚类并取平均。以5-mer ‘NLYFQ’为例, 图 1显示了用不同半径r得到的浓度矩阵彩图。从图 1可以看出,不同半径r得到的聚类位置不变;当半径增大时,聚类变得较为平坦。分别计算半径r=1,2,…, 20对应的聚类中心,并对不同半径下的聚类中心取平均作为最终聚类中心。
对PDB数据库中的5-mer扭转角聚类进行结构分类。根据拉氏图中的区域,将扭转角分为三种类型,即:α螺旋(包括左手和右手α螺旋)、β平面(平行和反平行β平面)、环(既非α螺旋又非β平面的扭转角被分为第三类)。对5-mer数据集Ω中的每一个5-mer的扭转角列表进行分类,根据扭转角列表中三种类型扭转角所占比例来确定该5-mer中间氨基酸的结构类型。如果该5-mer扭转角列表中主要为α类扭转角则认为该5-mer中间氨基酸为α类;若主要为β类扭转角,则认为该5-mer中间氨基酸为β类;若扭转角列表中的扭转角既非α类又非β类,则认为该5-mer中间氨基酸为环类;若α类和β类扭转角各半,则认为该5-mer中间氨基酸为α和β的混合类;类似地,还可以定义α、β和环三种结构的混合类,α和环的混合类,β和环的混合类。表 2列出了PDB数据库中所有5-mer中间氨基酸扭转角的统计信息。在所有5-mer中,中间氨基酸为α螺旋类的5-mer占比最高(29.21%), 其中以右手α螺旋居多;中间氨基酸为β平面类的5-mer占比为23.62%;中间氨基酸为α、β和环的混合类的5-mer占20.91%。α螺旋类5-mer的中间氨基酸主要为A, R, Q, E, L, K;β平面类5-mer的中间氨基酸主要为V, I, F, T, Y;α、β和环的混合类5-mer的中间氨基酸主要为S, L, D, A, E, T。
| 表 2 5-mer中间氨基酸的类型统计 Table 2 Structural type statistics for the middle amino acids of 5-mers |
表 2列出了PDB数据库中所有5-mer中间氨基酸的扭转角类型,第1列为5-mer的类型,第2、第3列分别为每种类型5-mer的数量和该种类型5-mer在整个5-mer数据集中所占比例,第4列为每种类型5-mer出现频率最高的中间氨基酸。
表 3和表 4总结了二十种常见氨基酸作为5-mer中间氨基酸时在每种类型5-mer中所占比例。表 3和表 4中第4~8列为每种类型5-mer对应二十种氨基酸所占比例,每一类的百分比之和均为100%。如表 3的第4列所示,在所有的α类型5-mer中,丙氨酸(A)作为中间氨基酸出现时的比例为8.49%,精氨酸(R) 作为中间氨基酸出现时的比例为6.35%,天冬氨酸(D)作为中间氨基酸出现时的比例为5.25%,其它氨基酸的情况如表 3所示。从表 3可以看出每种氨基酸偏好哪种类型的扭转角。例如,在α螺旋类5-mer中,丙氨酸(A)的比例最高(8.49%), 说明当5-mer中间氨基酸为丙氨酸时,其扭转角倾向于α螺旋类,或者说在α螺旋类的5-mer中,中间氨基酸为丙氨酸(A)的情况居多。类似地,从表 3第5列可以看出,左手α螺旋类的5-mer中,天冬氨酸(D)和天冬酰胺(N)比例最高,天冬氨酸(D)和天冬酰胺(N)在左手α螺旋类的5-mer中分别占比11.68%和26.11%,该比例明显高于其它氨基酸在左手α螺旋5-mer中所占的比例。
| 表 3 二十种氨基酸在每种5-mer类型中所占比例Ⅰ Table 3 Proportions of 20 amino acids in each 5-mer type(Ⅰ) |
| 表 4 二十种氨基酸在每种5-mer类型中所占比例Ⅱ Table 4 Proportions of 20 amino acids in each 5-mer type(Ⅱ) |
表中列出了每种5-mer类型中,对应20种常见氨基酸作为中间氨基酸出现时所占的比例。表中第1~8列,每一列的比例之和为100%。第1~3列分别为20氨基酸的名称、英文符号和缩写,第4~8列分别表示每种5-mer类型中,20种氨基酸作为5-mer中间氨基酸出现时所占比例。表 3中的5-mer类型分别为α螺旋、左手α螺旋、右手α螺旋、β平面和环。如第4列所示,所有α类5-mer中,丙氨酸(A)占8.49%,精氨酸(R)占6.35%,天冬氨酸(D)占5.25%,其它氨基酸的情况如表中所示。表中所示比例均为每种氨基酸作为5-mer中间氨基酸出现时的统计结果。
表 4中列出了每种5-mer类型中,20种常见氨基酸作为5-mer中间氨基酸出现时所占的比例。表 4第4~8列中,每一列的比例之和为100%。第1~3列分别为20种氨基酸的名称、英文符号和缩写,第4~8列分别为每种5-mer类型中,20种氨基酸作为5-mer中间氨基酸出现时所占比例。表 4中的5-mer类型分别为α和β的混合类、α和环的混合类、β和环的混合类,以及α、β和环的混合类。所有α和β的混合类5-mer中,丙氨酸(A)占7.29%,精氨酸(R)占5.61%,天冬氨酸(D)占3.61%,其它氨基酸的情况见表 4。
2.2 蛋白质的结构类型预测利用蛋白质的序列信息和PDB数据库中5-mer扭转角统计信息来预测蛋白质的结构类型。以两组随机抽取的CATH数据为例来阐述本方法的有效性。将蛋白质序列分为主要α类(C=1)、主要β类(C=2)、混合α和β类(C=3)这三种结构类型。
2.2.1 9组CATH数据的分类从CATH数据库中随机抽取9组CATH数据进行结构分类研究。这9组CATH数据分别来自CATH的三个主要结构类,从每个结构类中随机抽取3组数据。在保证每个结构类的蛋白质数量是均匀分布的前提下,CATH组的抽取是随机。这里所说的CATH组是指按CATH编号记录的组。整个数据集含有233条蛋白质序列,这9组CATH数据在每个结构类中的分布情况如表 5所示。下面仅通过蛋白质的序列信息来进行结构类型的预测。
| 表 5 九组CATH数据的分类 Table 5 Classification of 9 CATH groups |
表 5中前两列为CATH的三个主要结构类型与本例中每个结构类下的CATH组数,第3列为每个结构类下的蛋白质个数,第4~8列分别为蛋白质序列在5种不同分类方法下的分类准确率。
使用5-mer扭转角法对数据集中的蛋白质序列进行最优结构预测,并根据预测结果中氨基酸扭转角的偏好,将蛋白质序列分为3种结构类型。分类结果如表 5所示。将该方法所获得的分类结果与平均属性因子[17]、自然向量[18]、PseAAC[32]、Chou-Fasman[2]的分类结果进行比较,表中第4~8列分别为每种方法的分类准确率。表 5中的分类准确率是将每个结构类的蛋白质序列正确分类个数除以该类中蛋白质总个数而得到的。从表 4中可以看出该新方法可以有效地将这9组CATH数据进行结构分类,三种结构类型的分类准确率分别为87.18%、73.26%、79.71%,结构类型的预测效果较好。
平均属性因子和自然向量是两种蛋白质序列特征提取方法,其中平均属性因子是根据蛋白质的序列信息提取氨基酸物理属性的平均值作为蛋白质序列的特征向量[17],而自然向量提取的是蛋白质序列的氨基酸构成和排序,其中自然向量与氨基酸序列是一一对应的[18]。利用[17]中所述的最小平方误差MSE超平面对不同结构类型的蛋白质序列的平均属性因子向量和自然向量进行划分,从而实现对结构的分类。平均属性因子的分类准确率如表 5所示,其中第1类(C=1)的准确率为75.64%,第2类(C=2) 的准确率为74.42%,第3类(C=3)的准确率为76.81%。自然向量的分类结果为,第1类(C=1)准确率为84.62%,第2类(C=2)为91.76%,第3类(C=3)为82.61%。
PseAAC是支持向量机分类中常用的氨基酸序列特征提取方法,用多类支持向量机来对PseAAC特征进行分类,其分类结果如表 5所示。在PseAAC的分类结果中,三个结构类的分类准确率分别为第1类(C=1): 74.36%, 第2类(C=2): 67.44%, 第3类(C=3):69.57%。Chou-Fasman的分类结果为,第1类(C=1): 65.38%, 第2类(C=2): 82.43%, 第3类(C=3):62.69%。
上述所比较的五种分类方法都是通过蛋白质的氨基酸序列特征提取来进行结构分类或预测的,其中5-mer扭转角法是根据5-mer局部序列的扭转角统计偏好来进行结构类型的预测,而其它方法是通过对整条蛋白质序列进行特征提取来进行结构类型的预测的。通过比较这5种方法可以看出,5-mer扭转角法取得了较好的分类效果。
2.2.2 60组CATH数据的分类使用另一组随机抽取的CATH数据来验证新方法的有效性。这组数据含有60个CATH组共821条蛋白质序列[17]。这60组CATH数据取自CATH数据库的三个主要结构类:主要α结构(C=1);主要β结构(C=2);α与β混合结构(C=3)。本数据集来源于文献[17]中的结构分类,这60个CATH组的CATH编号详见本文附件材料。所使用的数据集与第1个例子中所使用的数据集是随机抽取的两组不同数据集,两个数据集之间没有交叉。利用5-mer扭转角法来对这60个CATH组的蛋白质序列进行结构类型的预测,并将预测结果与平均属性因子、自然向量、PseAAC和Chou-Fasman的结果进行比较。
为数据集中每一个蛋白质序列计算最优预测结构,并根据预测结构的扭转角偏好来进行结构类型的预测。CATH数据的信息和分类结果如表 6所示。在表 6中,5-mer扭转角法的分类结果最优,其分类准确率为:第1类(C=1): 98.97%;第2类(C=2): 77.24%;第3类(C=3): 67.57%。扭转角法的分类准确率较其它分类方法的准确率高,其中平均属性因子的分类准确率为:第1类(C=1): 66.15%;第2类(C=2): 56.55%;第3类(C=3): 73.18%。自然向量法的分类准确率为:第一1类(C=1): 57.44%;第2类(C=2): 40.69%;第3类(C=3): 86.90%。PseAAC的分类准确率为:第1类(C=1): 76.53%, 第二类(C=2): 66.90%, 第三类(C=3): 67.29%;Chou-Fasman的分类准确率为:第1类(C=1): 75.84%, 第2类(C=2): 64.93%, 第3类(C=3): 58.47%。
| 表 6 60个CATH组的分类结果 Table 6 Classification results of 60 CATH groups |
表 6中前3列分别为CATH的3个主要结构类以及每个结构类下的CATH组数和蛋白质个数。第4~8列分别为蛋白质序列在5种不同分类方法下的分类结果。
本例中,平均属性因子和自然向量在分类效果上与第1个例子存在差异,主要原因在于这两种方法利用最小平方误差超平面对高维实空间中的特征向量进行分类,由于不同数据集中的特征向量分布不同,因此得到的分类结果也不同。5-mer扭转角法的整体分类效果最好,其原因在于扭转角法利用5-mer局部序列的扭转角统计偏好来进行分类,在数据集较大时该方法充分利用了5-mer扭转角的统计特征,因此分类效果较好。
3 讨论基于5-mer中间氨基酸扭转角统计偏好的蛋白质结构类型预测方法是利用5-mer中间氨基酸的扭转角统计信息来进行蛋白质结构类型的预测。通过利用5-mer扭转角的统计特征进行结构预测,印证了局部蛋白质序列对结构的影响。通过CATH数据集的分析验证了新方法的有效性。所述该新方法可以通过MATLAB程序实现,能够仅通过蛋白质的序列信息来实现蛋白质结构类型的快速预测。
许多蛋白质分类方法通过蛋白质序列特征提取来实现结构和功能的分类。例如,自然向量法[18],k-串字典法[20],蛋白质映射[21-22],PseAAC等[32]。这些方法利用蛋白质序列中的氨基酸成分和排序来实现分类。其它分类方法,如LIBSVM等[33]机器学习方法,是监督型的分类方法,需要使用训练数据才能够进行分类。对于蛋白质的结构分类,机器学习分类方法占有很重要的地位[8-16, 33-37]。其它分类方法还有基于信息理论和网络分支的分类方法[38],该方法利用互信息和网络分支来对蛋白质的结构和序列进行分类。此外,平均属性因子[17]利用氨基酸的10种物理属性在序列中的平均值,来实现对蛋白质结构类型的分类[17, 39]。该方法从氨基酸物理属性的角度阐释了蛋白质序列与结构的关系。
其它蛋白质结构预测方法还有I-TASSER和Robetta等。这两种方法利用同源序列模板来实现蛋白质结构的预测[6-7],并以网络服务器的形式提供方法对应的服务。
利用最小序列单元即5-mer的扭转角统计偏好来进行蛋白质结构类型预测是一种新方法。该方法利用PDB数据库中5-mer中间氨基酸的扭转角统计偏好,验证了局部序列环境对结构的影响。该方法可以通过MATLAB编程实现,通过两组CATH数据验证了新方法的有效性。
研究表明,每种分类算法都具有一定的准确率,尽管随着科技的发展,分类的准确率会有所提高,然而由于计算误差以及序列和结构之间关系的复杂性,准确率上限仍然难以达到100%[40-43]。通过与平均属性因子、自然向量、PseAAC,以及Chou-Fasman的分类结果进行比较发现,该新方法的分类准确率整体优于其它分类方法,尤其是在大数据集的分类时优势明显,这是因为该方法充分利用了扭转角的统计特征来实现分类,当数据集较大时统计特征较明显。平均属性因子和自然向量法利用MSE超平面实现对序列特征向量的划分,其中MSE超平面是通过矩阵伪逆计算得到的,对每一个固定数据集来说,超平面的分类结果是唯一确定的。PseAAC方法利用支持向量机来进行分类,其分类结果较好;Chou-Fasman方法则通过计算氨基酸构象倾向因子来进行结构类型的预测,当数据集较大时其分类结果与PseAAC的结果相似。所比较的5种方法均利用氨基酸序列的特征来实现对结构的分类,每种方法的差异在于提取的序列特征角度不同。5-mer扭转角法侧重于利用局部序列环境对扭转角统计偏好的影响来进行分类,而其它方法则是对整个序列进行特征提取和分类。
研究结果表明局部序列环境对氨基酸扭转角的偏好具有一定影响,该结果可用于蛋白质序列的快速结构类型预测。在局部序列环境中,氨基酸扭转角的统计偏好与其相邻氨基酸的扭转角偏好有关。例如,在同一个α域中,相邻氨基酸倾向于具有相近的扭转角值,即骨干肽链中相邻氨基酸的扭转角具有相似的值,从而使得α螺旋形成一个稳定的结构。相邻氨基酸的扭转角偏好,以及在拼接过程中最优预测结构的选择,有助于蛋白质结构类型的正确分类。相反,在混合α和β结构类中,环和连接α(螺旋)和β(平面)区域的内聚部分不具有类似规律的模式,即混合结构的规律不如单纯α或单纯β结构的规律明显。因此,通过规律模式来对混合结构进行分类时,其准确率不如其它纯α或纯β结构的分类准确率高。尽管如此,三种结构类型仍然能够通过本文所述方法进行合理的分类。
蛋白质结构分类方法表明,局部序列环境对结构的选择具有重要影响。可以通过该新方法实现对新蛋白质序列结构类型的快速预测。
4 结论通过研究局部序列对氨基酸扭转角统计偏好的影响,提出了一种新的蛋白质结构类型预测方法,该方法利用5-mer中间氨基酸的扭转角统计偏好来预测蛋白质序列的结构类型。新方法可以快速地通过氨基酸序列实现结构类型的预测。研究验证了蛋白质局部序列对结构的影响,在一定程度上反映了蛋白质序列与结构之间的联系。
致谢 感谢北京化工大学提供研究场所和相关设施。
| [1] |
王举, 王兆月, 田心. 生物信息学基础及应用[M]. 北京: 清华大学出版社, 2014: 1-182. WANG Ju, WANG Zhaoyue, TIAN Xin. Bioinformatics: Fundementals and applications[M]. Beijing: Tsinghua University Press, 2014: 1-182. (  0) 0) |
| [2] |
CHOU P Y, FASMAN G D. Prediction of the secondary structure of proteins from their amino acid sequence[J]. Trends in Biochemical Sciences, 1977, 2(6): 128-131. DOI:10.1016/0968-0004(77)90440-6 (  0) 0) |
| [3] |
GARNIE J, GIBRAT J F, ROBSON B. GOR method for predicting protein secondary structure from amino acid sequence[J]. Methods in Enzymology, 1996, 266: 540-564. DOI:10.1016/S0076-6879(96)66034-0 (  0) 0) |
| [4] |
ROST B. PHD: Predicting 1D protein structure by profile based neural networks[J]. Methods Enzymology, 1996, 266: 525-539. DOI:10.1016/S0076-6879(96)66033-9 (  0) 0) |
| [5] |
WEI Y, THOMPSON J, FLOUDAS C. CONCORD: A consensus method for protein secondary structure prediction via mixed integer linear optimization[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 2012, 468: 831-850. DOI:10.1098/rspa.2011.0514 (  0) 0) |
| [6] |
ROY A, KUCUKURAL A, ZHANG Y. I-TASSER: A unified platform for automated protein structure and function prediction[J]. Nature Protocols, 2010, 5(4): 725-738. DOI:10.1038/nprot.2010.5 (  0) 0) |
| [7] |
KIM D E, CHIVIAN D, BAKER D. Protein structure prediction and analysis using the Robetta server[J]. Nucleic Acids Research, 2004, 32(2): W526-W531. DOI:10.1093/nar/gkh468 (  0) 0) |
| [8] |
DING C H, DUBCHAK I. Multi-class protein fold recognition using support vector machines and neural networks[J]. Bioinformatics, 2001, 17(4): 349-358. DOI:10.1093/bioinformatics/17.4.349 (  0) 0) |
| [9] |
EDLER L, GRASSMANN J, SUHAI S. Role and results of statistical methods in protein fold class prediction[J]. Mathematical and Computer Modelling, 2001, 33(12): 1401-1417. DOI:10.1016/S0895-7177(01)80022-4 (  0) 0) |
| [10] |
HUANG C D, LIN C T, PAL N R. Hierarchical learning architecture with automatic feature selection for multiclass protein fold classification[J]. IEEE Transactions on NanoBioscience, 2004, 2(4): 221-232. DOI:10.1109/TNB.2003.820284 (  0) 0) |
| [11] |
JO T, HOU J, EICKHOLT J, et al. Improving protein fold recognition by deep learning networks[J]. Scientific Reports, 2015, 5(1): 1-11. DOI:10.1038/srep17573 (  0) 0) |
| [12] |
KHAN M A, SHAHZAD W, BAIG A R. Protein classification via an ant-inspired association rules-based classifier[J]. International Journal of Bio-Inspired Computation, 2016, 8(1): 51-65. DOI:10.1504/IJBIC.2016.074631 (  0) 0) |
| [13] |
MARKOWETZ F, EDLER L, VINGRON M. Support vector machines for protein fold class prediction[J]. Biometrical Journal, 2010, 45(3): 377-389. DOI:10.1002/bimj.200390019 (  0) 0) |
| [14] |
TAN A C, GILBERT D, DEVILLE Y. Multi-class protein fold classification using a new ensemble machine learning approach[J]. Genome Informatics, International Conference on Genome Informatics, 2003, 14: 206-217. (  0) 0) |
| [15] |
WEI L, LIAO M, GAO X, et al. Enhanced protein fold prediction method through a novel feature extraction technique[J]. IEEE Transactions on NanoBioscience, 2015, 14(6): 649-659. DOI:10.1109/TNB.2015.2450233 (  0) 0) |
| [16] |
WEI L, ZOU Q. Recent progress in machine learning-based methods for protein fold recognition[J]. International Journal of Molecular Sciences, 2016, 17(12): 2118. DOI:10.3390/ijms17122118 (  0) 0) |
| [17] |
RACKOVSKY S. Sequence physical properties encode the global organization of protein structure space[J]. Proceedings of the National Academy of Sciences of the United States of America, 2009, 106(34): 14345-14348. DOI:10.1073/pnas.0903433106 (  0) 0) |
| [18] |
YU C, DENG M, CHENG S Y, et al. Protein space: A natural method for realizing the nature of protein universe[J]. Journal of Theoretical Biology, 2013, 318: 197-204. DOI:10.1016/j.jtbi.2012.11.005 (  0) 0) |
| [19] |
ZHAO B, HE R, YAU S T. A new distribution vector and its application in genome clustering[J]. Molecular Phylogenetics and Evolution, 2011, 59(2): 438-443. DOI:10.1016/j.ympev.2011.02.020 (  0) 0) |
| [20] |
YU C, HE R, YAU S T. Protein sequence comparison based on K-string dictionary[J]. Gene, 2013, 529(2): 250-256. DOI:10.1016/j.gene.2013.07.092 (  0) 0) |
| [21] |
YAU S T, YU C, HE R. A protein map and its application[J]. DNA and Cell Biology, 2008, 27(5): 241-250. DOI:10.1089/dna.2007.0676 (  0) 0) |
| [22] |
YU C, CHENG S Y, HE R, et al. Protein map: An alignment-free sequence comparison method based on various properties of amino acids[J]. Gene, 2011, 486(1/2): 110-118. DOI:10.1016/j.gene.2011.07.002 (  0) 0) |
| [23] |
MORIKAWA N. Discrete differential geometry of n-simplices and protein structure analysis[J]. Applied Mathematics, 2014, 5(16): 2458-2463. DOI:10.4236/am.2014.516237 (  0) 0) |
| [24] |
DUNITZ J. Pauling's left-handed α-helix[J]. Angewandte Chemie International Edition, 2001, 40(22): 4167-4173. DOI:10.1016/S0304-4238(01)00357-0 (  0) 0) |
| [25] |
TERWILLIGER T C. Rapid model building of alpha-helices in electron-density maps[J]. Acta Crystallographica Section D, 2010, 66(3): 268-75. DOI:10.1107/S0907444910000314 (  0) 0) |
| [26] |
SCHIFFER M, EDMUNDSON A B. Use of helical wheels to represent the structures of proteins and to identify segments with helical potential[J]. Biophysical Journal, 1967, 7(2): 121-135. DOI:10.1016/S0006-3495(67)86579-2 (  0) 0) |
| [27] |
KABSCH W, SANDER C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features[J]. Biopolymers, 1983, 22(12): 2577. DOI:10.1002/bip.360221211 (  0) 0) |
| [28] |
RICHARDSON J S. The anatomy and taxonomy of protein structure[J]. Advances In Protein Chemistry, 1981, 34: 167-339. DOI:10.1016/S0065-3233(08)60520-3 (  0) 0) |
| [29] |
LOVELL S C, DAVIS I W, ARENDALL W B, et al. Structure validation by Calpha geometry: phi, psi and Cbeta deviation[J]. Proteins, 2003, 50(3): 437-450. DOI:10.1002/prot.10286 (  0) 0) |
| [30] |
VOET D, VOET J G. Biochemistry[M]. 3rd ed. Hoboken, N J: Wiley, 2004: 227-231.
(  0) 0) |
| [31] |
XUE Q. Tools for analysis of DNA and protein sequence data[M]. 3rd ed. Beijing: Science Publishing, 2012: 71-117.
(  0) 0) |
| [32] |
SHEN H, CHOU K. PseAAC: A flexible web server for generating various kinds of protein pseudo amino acid composition[J]. Analytical Biochemistry, 2008, 373: 386-388. DOI:10.1016/j.ab.2007.10.012 (  0) 0) |
| [33] |
CHANG C, LIN C. LibSVM: A Library for support vector machines[J]. ACM Transactions on Intelligent Systems & Technology, 2011, 2(3): 27. DOI:10.1145/1961189.1961199 (  0) 0) |
| [34] |
CHEN J, GUO M, WANG X, et al. A comprehensive review and comparison of different computational methods for protein remote homology detection[J]. Briefings in Bioinformatics, 2018, 19(2): 231-244. DOI:10.1093/bib/bbw108 (  0) 0) |
| [35] |
LIN C, CHEN W, QIU C, et al. LibD3C: Ensemble classifiers with a clustering and dynamic selection strategy[J]. Neurocomputing, 2014, 123: 424-435. DOI:10.1016/j.neucom.2013.08.004 (  0) 0) |
| [36] |
LIN C, ZOU Y, QIN J, et al. Hierarchical classification of protein folds using a novel ensemble classifier[J]. PLoS One, 2013, 8(2): e56499. DOI:10.1371/journal.pone.0056499 (  0) 0) |
| [37] |
WEI L, LIAO M, GAO X, et al. An improved protein structural classes prediction method by incorporating both sequence and structure information[J]. IEEE Transactions On Nanobioscience, 2015, 14(4): 339-349. DOI:10.1109/TNB.2014.2352454 (  0) 0) |
| [38] |
WAN X, ZHAO X, HE R, et al. An information-based network approach for protein classification[J]. PLoS One, 2017, 12(3): e0174386. DOI:10.1371/journal.pone.0174386 (  0) 0) |
| [39] |
WAN X, TAN X. A study on separation of the protein structural types in amino acid sequence feature spaces[J]. PLoS One, 2019, 14(12): e0226768. DOI:10.1371/journal.pone.0226768 (  0) 0) |
| [40] |
ROST B, SANDER C. Prediction of protein secondary structure at better than 70% accuracy[J]. Journal of Molecular Biology, 1993, 232: 584-599. DOI:10.1006/jmbi.1993.1413 (  0) 0) |
| [41] |
RUSSELL R B, BARTON G J. The limits of protein secondary structure prediction accuracy from multiple sequence alignment[J]. Journal of Molecular Biology, 1993, 234: 951-957. DOI:10.1006/jmbi.1993.1649 (  0) 0) |
| [42] |
MONTGOMERIE S, SUNDARARAJ S, GALLIN W J, et al. Improving the accuracy of protein secondary structure prediction using structural alignment[J]. BMC Bioinformatics, 2006, 7: 301. DOI:10.1186/1471-2105-7-301 (  0) 0) |
| [43] |
FRANCESCO V D, GARNIER J, MUNSON P J. Improving protein secondary structure prediction with aligned homologous sequences[J]. Protein Science, 1996, 5: 106-113. DOI:10.1002/pro.5560050113 (  0) 0) |
 2021, Vol. 19
2021, Vol. 19

