Dekker等人于2002年就利用3c技术[1]用于重构酵母染色体的空间结构,由于受限于当时的技术条件,他们只进行了染色体区域内一对一的相互作用研究。近年来基于此技术发展出了4C[2],5C[3],Hi-c以及TCC技术[4],为染色体三维结构研究奠定了基础。4C是将DNA利用连接酶连接成环状后用特异PCR引物进行反向PCR,再对其产物进行分析得到染色体相互作用数据; 5C技术是在3c基础上增加了测序通量,主要用于研究染色体高频率的空间结构。而Hi-c技术[5]就是一种在3C基础上发展的高通量测序染色体全基因组的交互数据的生物信息学技术。随着基因组学的深入研究,人们发现染色体的相互作用数据在一定程度上可以反应基因组在三维空间的表达状况[6]。另一方面,相较于其他的3C衍生技术,利用Hi-c技术捕获到的全基因组交互数据为利用二维接触矩阵构建三维空间结构提供了可能。通过基因空间结构解析与传统转录数据相结合,研究人员可以更深入的阐释生物在基因调控以及表观遗传中的真实性状[7]。因此预测和重构染色体的三维结构对于后基因组时代研究具有指导意义。尽管目前部分染色体的组织结构可以通过电子显微镜进行研究。显微镜提供了单个细胞的信息,但分辨率相对较低; 而染色体构象捕获能获得高分辨率的染色体三维信息,极大拓展了我们对基因组的全面认识。
文中使用Duan等人研究使用的酵母数据样本[8],根据酵母16条染色体Hi-c数据构建了数据统计分布模型,在此基础上利用梯度优化算法预测并绘制了酵母染色体的三维结构图。
1 理论与方法利用Hi-c技术获得的基因组高通量染色体交互频率数据,通过特定数学模型预测基因组空间结构是重构染色体三维结构普遍采取的方法。其预测流程主要分为:Hi-c数据归一化处理; Hi-c数据转化为距离接触矩阵; 染色体三维重构模型; 和模型结果分析等。其中,Lieberman-Aiden等人曾对染色体上两个片段的接触频率和基因线性以及空间距离做了开创性研究,发现染色体片段之间的接触频率值与两个片段之间空间的距离成反比关系,即空间越接近则接触频率值越大,空间距离越远接触频率越小[9],在此原理上提出了以下距离转换关系式:
| $ {D_{ij}} = \left\{ \begin{array}{l} F_{ij}^{-1}, {F_{ij}} > 0\\ \infty, \;其他 \end{array} \right. $ | (1) |
式(1)中,Dij是表示酵母染色体上两个片段之间的通过转换的空间距离值,Fij表示酵母染色体片段间的接触频率值。
1.1 酵母染色体Hi-c数据分布拟合函数模型首先,需要对根据酵母染色体交互数据建立统计分布模型,为此,分别对酵母16条染色体的Hi-c数据分布情况进行高斯拟合,对每条染色体的数据我们都分别与高斯8个线性组合核函数进行拟合,再最终选取出拟合指标SSE, RMSE, R-square最优的高斯核函数,最终选取核函数的拟合指标结果如表 1所示。
| 表 1 16条染色体拟合情况表 Table 1 Fitting of 16 chromosomes |
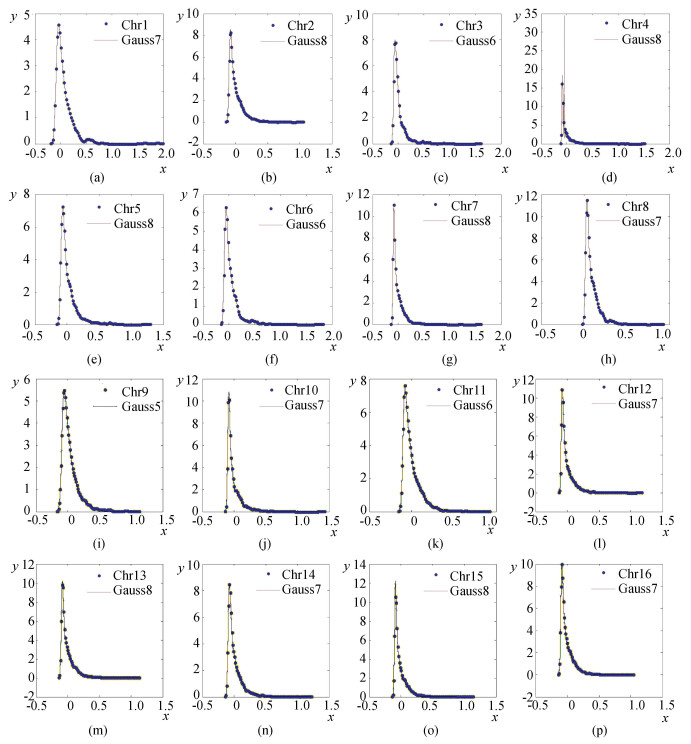
在最终确定了每条染色体拟合出对应的高斯核函数后,绘制了16条染色体Hi-c数据分布的拟合曲线(见图 1)。
|
图 1 染色体Hi-c数据分布拟合情况图 Figure 1 Fitting map of distribution of chromosome Hi-c data |
通过与酵母16条染色体交互数据分布拟合后,获得目标函数如下:
| $ \sum\limits_{n = 1}^m {{a_n}\exp \left( {-\frac{1}{{c_n^2}}\left( {D_i^s-D_i^2} \right)} \right)} $ | (2) |
式中,Dis是对应于Di的区域的欧几里德距离[10](i表示染色体上片段数),是由三维结构S中两个染色体片段区域的(x, y, z)坐标计算得到,an和cn是目标函数中的拟合参数。各参数见表 2所示。
| 表 2 酵母染色体Hi-c数据分布模型参数 Table 2 Parameters of yeast chromosome Hi-c data distribution model |
在似然估计中,用S表示酵母染色体结构,D表示从染色体交互数据导出的接触矩阵, 似然函数P(Di|S)表示在结构S条件下D中数据点概率[11],在此,真实的Hi-c数据分布由拟合得到的组合高斯模型代替,因此P(Di|S)可以表示为:
| $ P\left( {{D_i}|S} \right) \sim \sum\limits_{n = 1}^m {{a_n}\exp \left( {-\frac{1}{{c_n^2}}\left( {D_i^s-D_i^2} \right)} \right)} $ | (3) |
我们的目的是找到一个最大化似然函数的结构S*。式(3)中的目标函数仅依赖染色体结构中的(x, y, z)坐标。
1.3 梯度上升优化算法利用梯度上升算法对式(3)进行迭代优化,直到算法收敛为止。具体过程:如果使用新的(x, y, z)坐标计算的似然函数值和前一步的差值小于一个阈值,就认为算法收敛[11]。
梯度上升迭代优化中。利用等式(3)计算偏导数,再根据偏导采用梯度上升优化算法对各坐标进行调整,并按下式更新似然概率:
| $ {S^{\left( {t + 1} \right)}} = {S^{\left( t \right)}} + {\lambda ^{\left( t \right)}}\nabla L\left( {{S^{\left( t \right)}}} \right) $ | (4) |
式(4)中t是迭代索引指标,S(t)是迭代索引指标t的结构坐标,λ(t)是在t处的学习速率,随着迭代的进行可能发生变化,
| $ {g_{t, i}} = \nabla \left( {S_i^{\left( t \right)}} \right) $ | (5) |
| $ S_i^{\left( {t + 1} \right)} = S_i^{\left( t \right)} + {\lambda ^{\left( t \right)}}{g_{t, i}} $ | (6) |
在Ada Grad的迭代规则中,根据式(7),在参数Si的之前计算的梯度基础上,修正了每个参数Si在每一时间步长上的学习速率。
| $ S_i^{\left( {t + 1} \right)} = S_i^{\left( t \right)} + \frac{\lambda }{{\sqrt {{G_{t, ii}} + \varepsilon } }}{g_{t, i}} $ | (7) |
式中,Gt是一个对角元素为i的对角矩阵,i是Si的梯度平方和,如式(8)所示。其中Gt, ii是Gt中染色体片段i对应的值,而ε是一个平滑项,它是避免函数除以零(通常是1×10-6)。
| $ {G_t} = \sum\limits_{i = 1}^t {\left( {{g_i}{g_i}} \right)} $ | (8) |
Ada Grad的主要优点之一是它不需要在每次迭代时手动调整学习速率。
2 模型评价为了评估染色体三维结构模型的准确性,我们使用Pearson相关系数(PCC)、Spearman相关系数(SCC)这两个参数作为评价指标。假设两个模型的成对距离数据集,其中{di, ..., dn}有n个值,另一数据集{Di, ..., Dn}也含n个值,那么DPCC、DSCC可以使用以下公式来计算。
(1) 距离Pearson相关系数(DPCC)
定义为:
| $ {\rm{DPCC}} = \frac{{\sum\limits_{i = 1}^n {\left( {{d_i}-\bar d} \right)\left( {{D_i}-\bar D} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{d_i}-\bar d} \right)}^2}} } \sum\limits_{i = 1}^n {{{\left( {{D_i} - \bar D} \right)}^2}} }} $ | (9) |
其中,di和Di表示第i个距离样本值,n是成对距离的个数,
(2) 距离Spearman相关系数(DSCC)
定义为:
| $ DSCC = \frac{{\sum\limits_{i = 1}^n {\left( {{X_i}-\bar X} \right)\left( {{Y_i}-\bar Y} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{X_i}-\bar X} \right)}^2}} } \sum\limits_{i = 1}^n {{{\left( {{Y_i} - \bar Y} \right)}^2}} }} $ | (10) |
DSCC测量了两个三维结构距离剖面的相似性。DSCC值在-1.0和1.0之间变化,DSCC值越高,这两个结构就越相似。
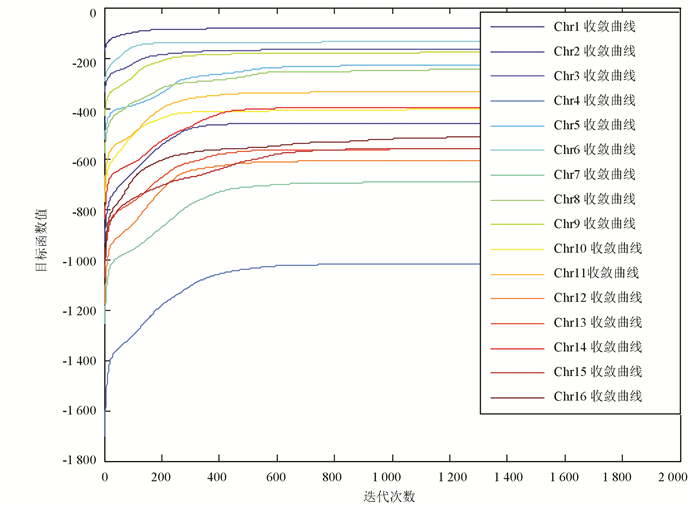
3 实验结果根据酵母16条染色体的Hi-c数据建立特定的分布函数,在此基础上构建目标函数,然后利用梯度上升算法对每条染色体Hi-c数据目标函数进行迭代,迭代的最大次数为2 000次,而收敛阈值设置为0.000 01,酵母16条染色体目标函数收敛曲线如图 2所示。
|
图 2 酵母16条染色体目标函数收敛曲线 Figure 2 Convergence curve of 16 chromosome objective functions in yeast |
从图 2中可以看出酵母16条染色体目标函数最终都达到收敛,说明该目标函数模型是有效可行的。文中使用梯度上升优化算法对酵母16条染色体数据进行三维空间结构重构,其模型的评价指标如表 3所示。
| 表 3 16条染色体结构Spearman和Pearson系数 Table 3 Spearman and Pearson coefficients of 16 chromosomal structures |
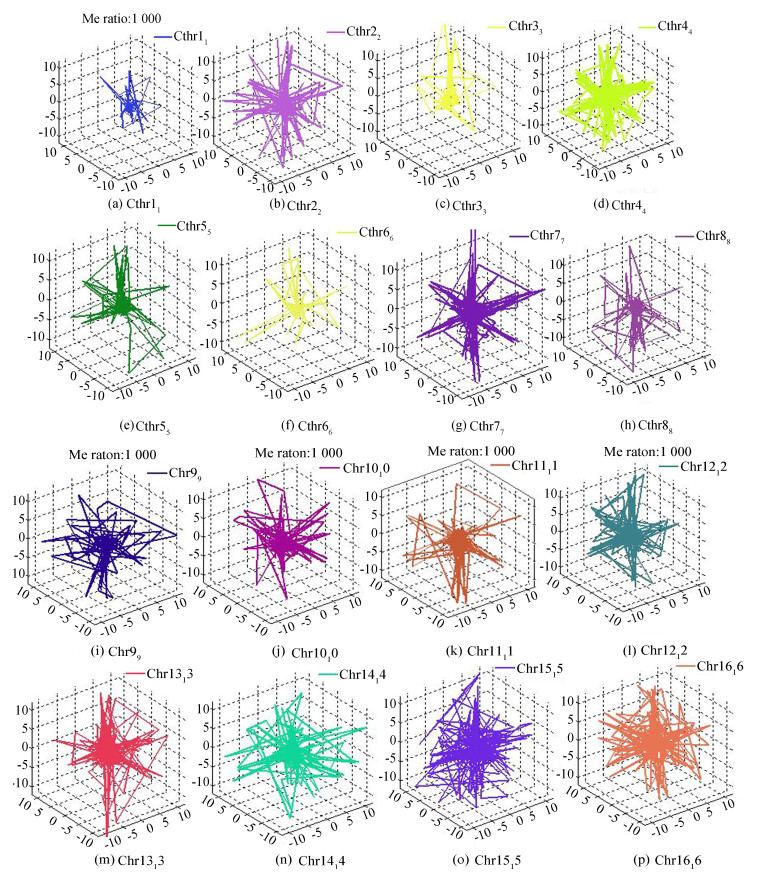
从表中可以看出,经过对每条染色体的Hi-c数据分布特征进行拟合出具体函数作为目标函数的模型的Spearman系数都达到了0.95以上,Pearson系数平均值也能达到0.71以上,说明对每条染色体进行Hi-c数据分布特征进行拟合出不同目标函数的方法来预测其结构是有效可行的。通过不同目标函数模型预测出的染色体结构如图 3所示。
|
图 3 16条染色体结构图 Figure 3 Charts of 16 chromosomal structures |
目前,利用染色体Hi-c交互数据预测三维空间结构大多根据单一分布模型,并没有考虑每条染色体数据的具体分布情况,而本文通过分析酵母16条染色体Hi-c数据的实际分布,从而拟合出更真实的分布模型,在此基础上利用梯度优化算法预测出较准确的染色体三维结构。但是为了分析方便,在对酵母16条染色体Hi-c数据进行距离转换时使用了统一的参数,后续我们将会针对具体染色体不同数据对转换函数的参数进行优化,增强模型的自适应性,从而进一步提高模型预测的准确性。
| [1] |
DEKKER J, RIPPE K, DEKKER M, et al. Capturing chromosome conformation[J]. Science, 2002, 295(5558): 1306-1311. DOI:10.1126/science.1067799 (  0) 0) |
| [2] |
ZHAO Z, TAVOOSIDANA G. Circular chromosome conformation capture (4C) uncovers extensive networks of epigenetically regulated intra- and inter-chromosomal interactions[J]. Nature Genetics, 2006, 38(11): 1341-7. DOI:10.1038/ng1891 (  0) 0) |
| [3] |
DOSTIE J, DEKKER J. Mapping networks of physical interactions between genomic elements using 5C technology[J]. Nature Protocols, 2007, 2(4): 988-1002. DOI:10.1038/nprot.2007.116 (  0) 0) |
| [4] |
KALHOR R, TJONG H, JAYATHILAKA N, et al. Genome architectures revealed by tethered chromosome conformation capture and population-based modeling[J]. Nature Biotechnology, 2011, 30(1): 90-98. DOI:10.1038/nbt.2057 (  0) 0) |
| [5] |
NAGANO T, LUBLING Y, STEVENS T J, et al. Single-cell Hi-C reveals cell-to-cell variability in chromosome structure[J]. Nature, 2013, 502(7469): 59. DOI:10.1038/nature12593 (  0) 0) |
| [6] |
ALT F W, ZHANG Y, MENG F L, et al. Mechanisms of programmed DNA lesions and genomic instability in the immune system[J]. Cell, 2013, 152(3): 417-429. DOI:10.1016/j.cell.2013.01.007 (  0) 0) |
| [7] |
DEKKER J. Gene regulation in the third dimension[J]. Science, 2008, 319(5871): 1793-1794. DOI:10.1126/science.1152850 (  0) 0) |
| [8] |
DUAN Z, ANDRONESCU M, SCHUTZ K, et al. A three-dimensional model of the yeast genome[J]. Nature, 2010, 465(7296): 363-367. DOI:10.1007/978-3-642-20036-6_28 (  0) 0) |
| [9] |
LIEBERMAN-AIDEN E, VAN BERKUM N L, WILLIAMS L, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome[J]. Science, 2009, 326(5950): 289-293. DOI:10.1126/science.1181369 (  0) 0) |
| [10] |
DEZA M M, DEZA E. Encyclopedia of distances[J]. Reference Reviews, 2009, 24(6): 1-583. DOI:10.1007/978-3-642-00234-2_19 (  0) 0) |
| [11] |
OLUWADARE O, ZHANG Y, CHENG J. A maximum likelihood algorithm for reconstructing 3D structures of human chromosomes from chromosomal contact data[J]. BMC Genomics, 2018, 19(1): 161. DOI:10.1186/s12864-018-4546-8 (  0) 0) |
 2019, Vol. 17
2019, Vol. 17

