核小体是真核生物染色质的基本结构单元,是DNA双螺旋缠绕在组蛋白八聚体上形成的复合物。标准的组蛋白八聚体由进化上高度保守的H2A、H2B、H3和H4各两个拷贝组成[1]。并非所有的核小体都由标准的组蛋白组装,全基因组范围内还富含一些组蛋白变体,如H2A.Z,H3.3等。组蛋白变体与标准组蛋白间存在一定的序列差异,对染色质结构和基因转录有不同的调控作用[2-4]。标准组蛋白和非标准组蛋白均由基因组上的若干个基因表达[3-4]。核小体核心DNA的长度约为147 bp [5-9],而相邻的核小体之间的链接DNA的长度并不恒定(约20-80 bp)。核小体核心颗粒在组蛋白H1的作用下形成30-nm结构,进一步组装成更高级结构[10],使基因组DNA包装到狭小的细胞核中。核小体占据真核基因组的绝大部分(约75%~90%)[11-12]。
核小体区域的DNA缠绕于组蛋白上,相比链接DNA不易于相关蛋白因子与之相接触并结合,从而导致核小体参与基因转录、DNA复制、修复、重组以及RNA剪接等众多生物学过程[11-15]。核小体在DNA序列以外的因素(如重塑蛋白、组蛋白修饰酶、细胞微环境变化等)或内在信号(DNA序列突变)的扰动下其位置时有发生变化并参与上述生物学过程[11-22]。体外的核小体定位只决定于DNA序列和相邻核小体之间的空间位阻效应[12]。而在体内,核小体则与一些DNA结合蛋白竞争结合基因组DNA,可能会导致DNA序列信号在核小体定位中的作用受到不同程度的影响;而且染色质重塑酶的作用也不可小觑,有时发挥单纯的催化功能影响核小体的组装效率,而有时ATP依赖的染色质重塑酶能使核小体发生位移[21-22]。尽管DNA序列的内在性质和序列以外的因素(如染色质重塑酶、蛋白因子与DNA序列的竞争结合等)在核小体定位中的重要性存在一定的争议[23-24],但体内和体外核小体定位图谱的高度相似性足以说明DNA序列是影响核小体定位的重要因素[12]。
过去几十年间发展了不少核小体定位的理论预测模型,这些模型与核小体实验图谱相结合促进了核小体定位机制与功能的研究[11-12, 18, 25-27]。理论预测模型中最常见的是基于DNA序列的预测模型,而这类预测模型又可大致分为基于DNA序列的生物信息学模型[12, 18, 28-36]和基于DNA变形能的生物物理学模型[37-45]。生物信息学模型中利用机器学习算法构建的模型不占少数。机器学习模型的建立与预测效果依赖于训练集数据,而生物物理学模型的建立主要借助于DNA物理特性和核小体晶体结构数据,并不需要训练集。生物物理学方法能够计算出DNA双螺旋缠绕组蛋白八聚体的变形能,从而预测DNA序列形成核小体的能力、全基因组水平上的核小体占据率和核小体形成自由能[37-45],也能够预测出核小体在DNA序列上的较为准确的位置(或中心位置)[40]。核小体的准确位置涉及核小体的两种定位方式,即平移定位和旋转定位[46],前者描述DNA序列与核小体核心区相对线性位置,而后者描述DNA双螺旋与组蛋白八聚体相对方向。一般来讲,旋转定位信号强的DNA区域具有较高的弯曲各向异性,即容易朝某一个特定方向弯曲缠绕组蛋白八聚体形成核小体。显然,旋转定位信号强的区域也是平移定位较稳定的区域。两种定位方式紧密关联,因此核小体在单碱基水平上的精确位置可借助旋转定位信息来预测。本文介绍预测核小体定位的生物物理学方法及其应用,旨在帮助人们更好地理解核小体定位,并建议选择性地使用这些模型。
1 基于DNA变形能的核小体定位预测方法结合核小体的晶体衍射结构数据,可以计算任意一条147 bp DNA片段在形成核小体的假定下的DNA变形能,并以此判断该DNA片段形成核小体的能力:变形能越小,DNA越容易弯曲,形成核小体的可能性越大。
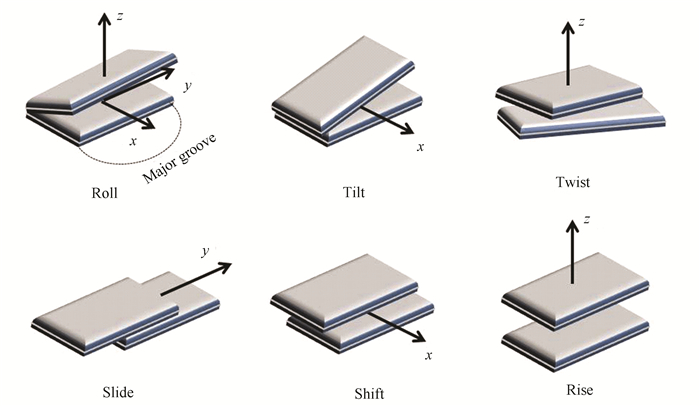
为了计算变形能(或弹性能),首先得科学描述DNA的几何结构。描述DNA构象的方法主要包括(见表 1):自由连接链模型[47-48]、蠕虫链模型[48-52]、圆形截面弹性杆模型[53-56]和碱基对梯阶模型[57-58]。自由连接链模型视高分子为由自由铰链(即连接处的弯曲方向与角度不受任何约束)连接多个独立的刚性片段而形成的分子。双链DNA分子中存在碱基对的氢键作用和碱基堆积作用,因此自由连接链模型不太适用于双链DNA。该模型本身也有一些缺陷,导致其应用受限[48]。蠕虫链模型被认为是更加接近真实高分子的粗粒化高分子链模型,其应用较广,但对于短于持久长度的DNA分子适用与否存在争议[51, 58]。国际上公认的另一种描述DNA结构的方法是碱基对阶梯模型(即剑桥协议方法[57]),即每一个碱基对上建立直角坐标系,并以相邻的坐标系之间的三个线位移和三个角位移描述DNA双螺旋结构(见图 1)。研究DNA结构的传统弹性杆模型(如虫链模型)中,将DNA看作是沿着序列连续弯曲的柔性杆,以DNA螺旋的骨架位形大致表示DNA的结构。而剑桥协议方法则极大地丰富了DNA结构的几何学,促进了DNA柔性估计[58]、DNA结构预测[59]、核小体定位[31, 37, 39-45]、启动子识别[60-62]、剪接位点识别[63]、重组热点识别[64-65]等多个与DNA结构相关的生物学问题的研究(见表 1)。
|
图 1 DNA双螺旋结构的碱基对梯阶模型 Figure 1 Base-pair step model for the DNA double helix structure 注:两个平板表示两个相邻的碱基对,其中一个板相对于另一板绕三个轴旋转的角位移(Tilt, Roll, Twist)和沿着三个轴方向平移的线位移(Shift, Slide, Rise)是模型中的六个结构参数. |
| 表 1 常用的DNA构象描述方法与应用 Table 1 Frequently-used methods to describe the DNA conformation and their applications |
计算DNA变形能需预先知道描述二核苷酸弯曲能力的力常数。不同的二核苷酸有不同的力常数,同一个二核苷酸的不同的结构变化(如Slide, Shift, Rise, Roll, Tilt, Twist的变化)对应不同的力常数。力常数的计算主要有三种方法:基于DNA解链温度的测定[37-38]、基于DNA结构数据的计算[40, 43, 66-67]和分子动力学模拟方法[45, 68],下面重点介绍其中最常用的一种,即基于DNA结构数据的力常数计算[67]。
令θn代表剑桥协议下参数符号,n=1, 2, 3, 4, 5, 6分别对应Ω、ρ、τ、DX、Dy和DZ。利用晶体结构数据库(如DNA-蛋白复合物的晶体结构数据)[69]计算每一种二核苷酸的结构参数相对于所有二核苷酸的结构参数平均值的涨落:
| $ \Delta \theta_{n}=\theta_{n}-\theta_{0} $ |
力常数的逆与结构参数涨落的协方差之间的关系为[52]:
| $ \left[F^{-1}\right]_{n m}=<\Delta \theta_{n} \Delta \theta_{m}>/ k T $ | (1) |
其中k为玻尔兹曼常数,T为室温(单位为开尔文),< ΔθnΔθm>= < θnθm>- < θn> < θm>。
根据式(1)计算力常数矩阵。力常数矩阵中对角元表示各种结构参数对应的力常数,而非对角元反映同一种二核苷酸的不同结构参数间的耦合关联,是属于二阶微量。
弹性杆模型中,任一147 bp长度的DNA序列的弹性能可近似用平衡态附近的二次势能函数表示为[52]:
| $ E_{e l}=\frac{1}{2} \sum\limits_{i=1}^{146} \boldsymbol{\theta}_{i}^{\mathrm{T}} F_{i} \boldsymbol{\Theta}_{i} $ | (2) |
其中Θ为由Δθn构成的矩阵,ΘiT表示Θi的转置,Fi表示序列中第i个位置二核苷酸的力常数矩阵。
Tolstorokov等利用该模型预测了体外组装的4个核小体在DNA序列上的位置,发现能量最低值(能量越低,越容易形成核小体)与核小体位置非常吻合[42]。他们的研究又表明roll和slide是决定核小体DNA超螺旋结构的最主要参数。
Morozov等提出的预测核小体定位的弹性能模型中[43],核小体DNA可从最初的超螺旋结构进一步调整(微调)。故核小体DNA的自由能由两部分组成,
| $ E=E_{e l}+w E_{s h} $ | (3) |
其中Eel表示序列特异的DNA弹性能,Esh表示组蛋白与DNA的相互作用能,即由组蛋白与DNA的相互作用导致的核小体DNA相对于理想超螺旋结构的偏离所对应的能量。在此基础上定义核小体起始概率和占据率[43],成功预测了6个体外核小体的中心位置(能量的最小值较好地吻合核小体的中心位置)。
Miele等的基于能量的核小体定位预测模型[41]是依据与核小体晶体衍射结构(1kx5)最吻合的理想超螺旋结构建立的。假定DNA序列是不可伸长且不发生切变的弹性棒,而核小体形成时DNA的变形只由twist, roll和tilt造成,变形能表示为:
| $ \begin{align} & \frac{\Delta E}{kT}=\sum\limits_{i=1}^{146}{\left( \frac{{{A}_{1}}}{2}{{\left[ \rho (i)-{{\rho }_{0}}(i) \right]}^{2}}+\frac{{{A}_{2}}}{2}{{\left[ \tau (i)-{{\tau }_{0}}(i) \right]}^{2}}+ \right.} \\ & \left. \ \ \ \ \ \ \ \ \ \frac{{{A}_{3}}}{2}{{\left[ \omega (i)-{{\omega }_{0}}(i) \right]}^{2}} \right) \\ \end{align} $ | (4) |
其中各个位点上的结构参数(ρ(i),τ(i),ω(i))由核小体DNA的理想超螺旋结构获得;roll, tilt和twist的平衡结构参数值(ρ0,τ0,ω0)和力常数(A1,A2,A3)从Anselmi等的工作获得[37]。这里的力常数并不是利用DNA-蛋白质复合物的晶体结构数据计算得到的。A1和A2是与DNA的弯曲(弯曲主要由roll和tilt导致)相关的力常数,而A3是与DNA的扭转(Twist)相关的力常数。由于二核苷酸向roll方向和tilt方向的弯曲刚度(或劲度)是各向异性的,对于任一二核苷酸来讲其力常数A1和A2原则上是不一样的。但很多工作中通常忽略弯曲的各向异性,以二者相等作为近似。这些力常数是以DNA的扭转刚度和弯曲刚度相关的力常数乘以序列依赖的调节因子来表示,如${{A}_{1}}={{A}_{2}}=a\left(\frac{T}{{{T}^{*}}} \right), {{A}_{3}}=b\left(\frac{T}{{{T}^{*}}} \right)$,其中a和b为由实验估计的一个常数,而调节因子$\frac{T}{{{T}^{*}}}$依赖于不同二核苷酸的解链温度(二核苷酸的解链温度与其堆积能正相关),是实验上测定的解链温度与标准DNA序列的平均解链温度的比值。考虑序列从自由DNA变成核小体超螺旋结构时对应的熵变ΔS,则形成核小体时DNA的自由能表示为:
| $ \frac{\Delta F}{k T}=\frac{\Delta E}{k T}-\Delta S $ | (5) |
用该模型预测酵母和果蝇核小体占据率时,能够准确预测转录起始等调控区域的核小体缺乏区,但对整个基因组范围的核小体占据率的预测精度不是很高(如酵母第3号染色体的核小体占据率的预测结果与实验数据[70]的相关系数R=0.45, P < 10-15)。
De Santis等提出的预测核小体形成自由能的统计热力学模型[37-38]与Miele的模型[41]相似,同样是计算twist, roll和tilt对应的自由能,但不包含核小体形成对应的熵变这一项。用该模型预测的一些酵母基因组区域的形成核小体的自由能与实验测定的核小体占据率相吻合,而且预测的100个核小体DNA的自由能与实验测定的自由能之间有很强的正相关性(R=0.92,P < 0.001)[37]。
Deniz等建立的DNA变形能模型[45],形式上与式(2)相同,但其物理意义与前几种模型不同。该模型计算的变形能是用来表示使自由DNA片段的结构变为核小体DNA结构的变形能。这里,所谓的核小体DNA的结构指的是描述核小体DNA结构的每个碱基对梯阶(Base-pair step)对应的六个坐标自由度(见图 1),这些坐标通过对多个X射线晶体衍射核小体DNA结构进行平均后获得。而初始的平衡态自由DNA结构则通过对少量的双链DNA(但包含所有约化的10种二核苷酸)在水环境中的分子动力学模拟获得。相关的力常数通过计算平衡态自由DNA结构参数的协方差获得(注:力常数矩阵是协方差矩阵的逆)。利用该模型,作者发现核小体缺乏区域的DNA变形能明显高于其侧翼序列,说明该区域从DNA序列的物理特性对核小体的形成有重要影响。
我们的模型[40, 71-74]中主要考虑DNA弯曲和切变对应的变形能,称之为弯曲能和切变能。
缠绕组蛋白八聚体时DNA的弯曲主要取决于roll和tilt。假定导致DNA弯曲的扭力Fb均匀分布在DNA链上,则roll和tilt角的偏离平衡态的程度用下式表示:
| $ \left\{\begin{array}{l}{\rho(i)-\rho_{0}(i)=F_{b} \cos \Omega_{i} / k_{\rho}(i)} \\ {\tau(i)-\tau_{0}(i)=F_{\mathrm{b}} \sin \Omega_{i} / k_{\tau}(i)}\end{array}\right. $ | (6) |
其中i表示碱基对出现的位置,ρ0表示DNA的平均转角,τ0表示DNA的平均倾角,kρ和kτ分别是转角和倾角对应的力常数,均由DNA-蛋白复合物的晶体结构数据获得[40]。Ωi表示从核小体中心位置(二分轴)向两侧计算的累加的扭角,其中每种碱基对梯阶对应的扭角是来自大量DNA-蛋白复合物的平均扭角。其实,所有碱基对梯阶的扭角均取为w(i)=360°/10.4(核小体结构NCP147的平均扭角)对结果的影响微乎其微。
在第i碱基对梯阶中DNA的弯曲能为:
| $ \begin{array}{c}{E_{\mathrm{b}}(i)=\frac{1}{2} k_{\rho}(i)\left[^{\rho}(i)-\rho_{0}(i)\right]^{2}+} \\ {\frac{1}{2} k_{\tau}(i)\left[\tau(i)-\tau_{0}(i)\right]^{2}=} \\ {\frac{F_{\mathrm{b}}^{2}}{2 k_{\rho}(i)} \cos ^{2} \mathit{\Omega }_{i}+\frac{F_{\mathrm{b}}^{2}}{2 k_{\tau}(i)} \sin ^{2} \mathit{\Omega }_{i}}\end{array} $ | (7) |
长度为L碱基对的DNA片段弯曲时,总的弯曲能为:
| $ \begin{aligned} E_{\mathrm{b}} &=\sum\limits_{-(L-1) / 2}^{(L-1) / 2} E_{\mathrm{b}}(i)=\\ & \sum\limits_{-(L-1) / 2}^{(L-1) / 2}\left[\frac{F_{\mathrm{b}}^{2}}{2 k_{\rho}(i)} \cos ^{2} \mathit{\Omega }_{i}+\frac{F_{\mathrm{b}}^{2}}{2 k_{\tau}(i)} \sin ^{2} \mathit{\Omega }_{i}\right] \end{aligned} $ | (8) |
其中扭力Fb通过以下约束条件获得[9, 40]。在核小体上,扭力Fb的作用下129 bp长度的DNA(注:核小体DNA两端各9 bp的区域是相对直的[9],计算弯曲能时不考虑)在组蛋白八聚体上缠绕579度。而这579度(α)的弯曲(或缠绕)是由描述DNA双螺旋结构的ρ和τ角共同造成的。因此形成核小体的约束条件为:
| $ \alpha=\sum\limits_{i}\left[\rho(i) \cos \mathit{\Omega }_{i}+\tau(i) \sin \mathit{\Omega }_{i}\right] $ | (9) |
结合式(6)可得
| $ F_{\mathrm{b}}=\frac{\alpha-\sum\limits_{i} \rho_{0}(i) \cos \mathit{\Omega }_{i}-\sum\limits_{i} \tau_{0}(i) \sin \mathit{\Omega }_{i}}{\sum\limits_{i} \frac{\cos ^{2} \mathit{\Omega }_{i}}{k_{p}(i)}+\sum\limits_{i} \frac{\sin ^{2} \mathit{\Omega }_{i}}{k_{\tau}(i)}} $ | (10) |
同理,结合核小体DNA的另一结构约束条件(螺距)可得DNA切变能。
基于变形能可用玻尔兹曼分布近似估计序列形成核小体的潜能[40]。更普遍的做法是,将每一条染色体上的核小体分布看作是多个全同粒子(组蛋白八聚体)在一长链DNA分子上的分布,以变形能为基础,用巨正则系综理论计算出核小体在每一个147 bp序列片段上形成的概率,再通过概率加和计算出DNA位点上的核小体占据率[40, 43]。具体计算方法如下:
假定$\beta=\frac{1}{k T}=1$,则由M-bp长度的粒子(即核小体)沿长度为N-bp的DNA序列分布的系统的巨配分函数为:
| $ Z=\sum\limits_{\text { conf }} e^{-[E(\operatorname{conf})-\mu n(\operatorname{conf})]} $ | (11) |
其中conf表示与DNA结合的非重叠粒子的任一构象,μ表示化学势,E(conf)和n(conf)分别表示任一构象对应的总能量和总粒子数。
巨配分函数由一系列正向配分函数(从DNA序列的某一端开始计算)的递进求解计算:
| $ Z_{j}^{f}=\left\{ \begin{align} & 1, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ j=0, 1, \ldots , M-1 \\ & Z_{j-1}^{f}+Z_{j-M}^{f}{{e}^{-\left( {{E}_{j-M+1}}-\mu \right)}}, j=M, M+1, \ldots , N \\ \end{align} \right. $ | (12) |
用同样的方式计算反向的配分函数(从DNA序列的另一端开始计算):
| $ \begin{array}{l} \;\;Z_j^\prime = \\ \left\{ \begin{array}{l} 1, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = N - M + 2, N - M + 3, \ldots , N + 1\\ Z_{j + 1}^r + Z_{j + \mu }^r{e^{ - \left( {{E_j} - \mu } \right)}}, j = N - M + 1, N - M, \ldots , 1 \end{array} \right. \end{array} $ | (13) |
其中ZNf=Z1r=Z。
粒子(核小体)从第j个位点起始的概率(考虑了空间位阻效应)为:
| $ P_{j}=\frac{Z_{j-1}^{f} e^{-\left(E_{j}-\mu\right)} Z_{j+M}^{r}}{Z} $ | (14) |
第j个位点被核小体占据的概率为:
| $ O_{j}=\sum\limits_{i=j-(L-1)}^{j} P_{i} $ | (15) |
核小体占据率的计算以统计物理学巨正则系综理论为基础,考虑相邻核小体空间位阻效应。核小体占据率的另一种估算方法以Percus方程为基础[75]。若s位点的核小体DNA的变形能为E(s),分析核小体的组装(即组蛋白八聚体沿DNA链的组装)过程时,可将染色质模拟为在外势场E(s)中的有限长度l(核小体核心DNA长度,约等于147)的一维杆系统(流体)。热力学巨正则系统描述中,系统被视为处于温度项为β的热浴环境和化学势为μ的组蛋白八聚体热库中,系统在外势场E(s)中达到热力学平衡时其密度服从非线性积分方程(即Percus方程):
| $ \begin{array}{l} \beta \mu = \beta E(s) + \ln \rho (s) - \ln \left( {1 - \int_s^{ s + l} \rho \left( {s{'}} \right)ds{'}} \right) + \\ \int_{s - l}^s {\frac{{\rho \left( {s{'}} \right)}}{{1 - \int_{s{'}}^{s{'} + l} \rho \left( {s{"}} \right)ds{"}}}} ds{'} \end{array} $ | (16) |
获得核小体密度的基础上利用窗口大小为147 bp的矩形函数计算核小体占据率:
| $ \operatorname{OCC}(s)=\rho(s) \cdot \mathit{\Pi }_{147}(s) $ | (17) |
我们的变形能模型能较好地预测体外核小体占据率、体外组装的核小体在DNA序列上的准确位置、以及体外组装核小体的自由能(即核小体的稳定性)[40, 72]。尤其是DNA弯曲能在核小体准确位置[40]和核小体滑动模式[72]的研究中有很好的应用前景。模型中用到的描述DNA结构的碱基对梯阶参数也能较好地区分核小体富含区和核小体缺乏区[76]。
还有一些模型中除了DNA序列依赖的简谐能以外还考虑了组蛋白和DNA之间的物理接触位点上的相互作用[77]。另外,有一些模型中虽然用到DNA螺旋结构参数[30]或其他DNA物理特征[31],抑或是涉及DNA弯曲度[33],但这些模型本质上是属于生物信息学方法,因为模型中主要是利用从序列提取的特征信息或DNA物理特征预测核小体的位置,而不涉及DNA变形能的计算。
2 讨论预测核小体定位的生物信息学方法和生物物理学方法的主要区别在于:(1)生物信息学方法通常是使用大量的可靠数据来训练模型[28-30],但生物物理学方法是基于DNA的物理化学性质(如二核苷酸的弯曲特性等)[37-45];(2)由于体内核小体定位还与其它非DNA因素有关,而且这种非DNA因素也可能是物种特异的(如物种特异的核小体定位模体),基于不同物种核小体数据训练的生物信息学方法的预测结果可能会优于单纯基于DNA物理化学性质的生物物理学方法;(3)生物物理学方法能够很好地预测核小体的中心位置及其可能的旋转定位[40],但只有少量的、设计巧妙的生物信息学方法才能做到这一点[34];(4)与生物信息学方法相比,生物物理学方法的物理意义更加明了,有助于理解问题本质。总的来说,生物信息学方法和生物物理学方法各有利弊。
各种生物物理学方法的主要差异包括:(1)使用的力常数不同,如有的用DNA-蛋白复合物的结构数据基础上计算的力常数[40, 43],而有的用二核苷酸的解链温度表征其力常数[37];(2)使用的DNA结构参数不同,如有的用twist, roll, tilt, 有的用twist, roll, slide, 有的用roll, tilt, slide, 而有的用所有6种结构参数;(3)预测核小体形成能力的最终指标中所包含的成分不同,如有的包含变形能和熵变,有的包含变形能和DNA-组蛋白相互作用能,有的只有变形能成分;(4)使用的核小体模型不同,如有的用核小体核心颗粒的真实DNA结构模型[43],而有的用与核小体核心颗粒DNA拟合最好的理想的超螺旋结构模型。
我们认为,预测核小体定位时有以下问题值得注意:(1)力常数、平衡结构参数的估算准确与否直接影响模型的预测结果,而这些参数的估计中需要注意DNA螺旋不同结构参数之间的耦合相互作用[78-79],计算原理的可靠性(如基于核小体DNA结构的实验数据的力常数计算和基于分子动力学模拟的力常数计算)和计算用的实验数据量(如DNA-蛋白复合物或核小体DNA的晶体结构数据);(2)预测能力从以下三个角度评价:核小体占据率的预测、核小体中心位置的预测、核小体装配自由能的预测和核小体移动位置的预测,而不能只看其中一方面;(3)基于DNA序列的核小体定位预测模型应该用体外核小体定位序列训练模型,预测结果应与体外核小体定位数据相比较,这样能够挖掘核小体定位对DNA序列的依赖本质;(4)核小体定位预测模型的最终目标应该是准确预测体内核小体的位置,因为只有这样才能使我们的预测本身更具有生物学意义。
总体而言,基于DNA序列预测酵母核小体定位的生物物理学方法取得了很大的进展,而且该类方法相对机器学习类生物信息学方法而言其物理意义清晰,但仍存在一些问题有待解决,例如:模型中的参数强烈依赖于DNA序列片段的物理性质,不同长度、不同序列模式其物理意义可能存在很大的差异,这些都会直接地影响模型中参数的准确估计以及模型的应用效果;模型中的有些近似假设需要更坚实的依据;不同的模型其侧重点不同,适用问题(如核小体占据率的预测、核小体在序列上准确位置的预测、核小体稳定性的预测以及核小体形成能力的预测)也略有不同;特定环境或过程中(如RNA聚合酶竞争性结合、组蛋白的化学修饰、染色质重塑等)核小体定位会发生变化,这需要更专一的生物物理模型才能回答。
| [1] |
LUGER K, MÄDER A W, RICHMOND R K, et al. Crystal structure of the nucleosome core particle at 2.8A resolution[J]. Nature, 1997, 389(6648): 251-260. DOI:10.2210/pdb1aoi/pdb (  0) 0) |
| [2] |
WEBER C M, HENIKOFF S. Histone variants: Dynamic punctuation in transcription[J]. Genes & Development, 2014, 28(7): 672-682. DOI:10.1101/gad.238873.114 (  0) 0) |
| [3] |
SOBOLEVA T A, NEKRASOV M, RYAN D P, et al. Histone variants at the transcription start-site[J]. Trends in Genetics, 2014, 30(5): 199-209. DOI:10.1016/j.tig.2014.03.002 (  0) 0) |
| [4] |
XIONG C, WEN Z, LI G. Histone Variant H3.3: A versatile H3 variant in health and in disease[J]. Science China Life Sciences, 2016, 59(3): 245-256. DOI:10.1007/s11427-016-5006-9 (  0) 0) |
| [5] |
BATTISTINI F, HUNTER C A, GARDINER E J, et al. Structural mechanics of DNA wrapping in the nucleosome[J]. Journal of Molecular Biology, 2010, 396(2): 264-279. DOI:10.1016/j.jmb.2009.11.040 (  0) 0) |
| [6] |
LUGER K, RECHSTEINER T J, FLAUS A J, et al. Characterization of nucleosome core particles containing histone proteins made in bacteria[J]. Journal of Molecular Biology, 1997, 272(3): 301-311. DOI:10.1006/jmbi.1997.1235 (  0) 0) |
| [7] |
ONG M S, RICHMOND T J, DAVEY C A. DNA stretching and extreme kinking in the nucleosome core[J]. Journal of Molecular Biology, 2007, 368(4): 1067-1074. DOI:10.1016/j.jmb.2007.02.062 (  0) 0) |
| [8] |
LUGER K, RICHMOND T J. DNA binding within the nucleosome core[J]. Current Opinion in Structural Biology, 1998, 8(1): 33-40. DOI:10.1016/S0959-440X(98)80007-9 (  0) 0) |
| [9] |
RICHMOND T J, DAVEY C A. The structure of DNA in the nucleosome core[J]. Nature, 2003, 423(6936): 145-150. DOI:10.1038/nature01595 (  0) 0) |
| [10] |
MAESHIMA K, IMAI R, TAMURA S, et al. Chromatin as dynamic 10-nm fibers[J]. Chromosoma, 2014, 123(3): 225-237. DOI:10.4161/nucl.26053 (  0) 0) |
| [11] |
LEE W, TILLO D, BRAY N, et al. A high-resolution atlas of nucleosome occupancy in yeast[J]. Nature Genetics, 2007, 39(10): 1235-1244. DOI:10.1038/ng2117 (  0) 0) |
| [12] |
KAPLAN N, MOORE I K, FONDUFE-MITTENDORF Y, et al. The DNA-encoded nucleosome organization of a eukaryotic genome[J]. Nature, 2009, 458(7236): 362-366. DOI:10.1038/nature07667 (  0) 0) |
| [13] |
MACALPINE D M, ALMOUZNI G. Chromatin and DNA replication[J]. Cold Spring Harbor Perspectives in Biology, 2013, 5(8): a010207. DOI:10.1101/cshperspect.a010207 (  0) 0) |
| [14] |
YAMADA T, OHTA K. Initiation of meiotic recombination in chromatin structure[J]. Journal of Biochemistry, 2013, 154(2): 107-114. DOI:10.1093/jb/mvt054 (  0) 0) |
| [15] |
NAFTELBERG S, SCHOR I E, AST G, et al. Regulation of alternative splicing through coupling with transcription and chromatin structure[J]. Annual Review of Biochemistry, 2015, 84(1): 165-198. DOI:10.1146/annurev-biochem-060614-034242 (  0) 0) |
| [16] |
FIELD Y, KAPLAN N, FONDUFE-MITTENDORF Y, et al. Distinct modes of regulation by chromatin encoded through nucleosome positioning signals[J]. PLoS Computational Biology, 2008, 4(11): e1000216. DOI:10.1371/journal.pcbi.1000216 (  0) 0) |
| [17] |
LEE C K, SHIBATA Y, RAO B, et al. Evidence for nucleosome depletion at active regulatory regions genome-wide[J]. Nature Genetics, 2004, 36(8): 900-905. DOI:10.1038/ng1400 (  0) 0) |
| [18] |
SEGAL E, FONDUFE-MITTENDORF Y, CHEN L, et al. A genomic code for nucleosome positioning[J]. Nature, 2006, 442(7104): 772-778. DOI:10.1038/nature04979 (  0) 0) |
| [19] |
SATCHWELL S C, DREW H R, TRAVERS A A. Sequence periodicities in chicken nucleosome core DNA[J]. Journal of Molecular Biology, 1986, 191(4): 659-675. DOI:10.1016/0022-2836(86)90452-3 (  0) 0) |
| [20] |
STRUHL K, SEGAL E. Determinants of nucleosome positioning[J]. Nature Structural & Molecular Biology, 2013, 20(3): 267-273. DOI:10.1038/nsmb.2506 (  0) 0) |
| [21] |
PARTENSKY P D, NARLIKAR G J. Chromatin remodelers act globally, sequence positions nucleosomes locally[J]. Journal of Molecular Biology, 2009, 391(1): 12-25. DOI:10.1016/j.jmb.2009.04.085 (  0) 0) |
| [22] |
NARLIKAR G J, SUNDARAMOORTHY R, OWEN-HUGHES T. Mechanisms and functions of ATP-dependent chromatin-remodeling enzymes[J]. Cell, 2013, 154(3): 490-503. DOI:10.1016/j.cell.2013.07.011 (  0) 0) |
| [23] |
MAVRICH T N, IOSHIKHES I P, VENTERS B J, et al. A barrier nucleosome model for statistical positioning of nucleosomes throughout the yeast genome[J]. Genome Research, 2008, 18(7): 1073-1083. DOI:10.1101/gr.078261.108 (  0) 0) |
| [24] |
ZHANG Y, MOQTADERI Z, RATTNER B P, et al. Intrinsic histone-DNA interactions are not the major determinant of nucleosome positions in vivo[J]. Nature Structural & Molecular Biology, 2009, 16(8): 847-852. DOI:10.1038/nsmb.1636 (  0) 0) |
| [25] |
BROGAARD K, XI L, WANG J P, et al. A map of nucleosome positions in yeast at base-pair resolution[J]. Nature, 2012, 486(7404): 496-501. DOI:10.1038/nature11142 (  0) 0) |
| [26] |
VALOUEV A, ICHIKAWA J, TONTHAT T, et al. A high-resolution, nucleosome position map of C. elegans reveals a lack of universal sequence-dictated positioning[J]. Genome Research, 2008, 18(7): 1051-1063. DOI:10.1101/gr.076463.108 (  0) 0) |
| [27] |
SCHONES D E, CUI K, CUDDAPAH S, et al. Dynamic regulation of nucleosome positioning in the human genome[J]. Cell, 2008, 132(5): 887-898. DOI:10.1016/j.cell.2008.02.022 (  0) 0) |
| [28] |
PECKHAM H E, THURMAN R E, FU Y, et al. Nucleosome positioning signals in genomic DNA[J]. Genome Research, 2007, 179(8): 1170-1177. DOI:10.1101/gr.6101007 (  0) 0) |
| [29] |
XING Y, ZHAO X, CAI L. Prediction of nucleosome occupancy in Saccharomyces cerevisiae using position-correlation scoring function[J]. Genomics, 2011, 98(5): 359-366. DOI:10.1016/j.ygeno.2011.07.008 (  0) 0) |
| [30] |
GUO S H, DENG E Z, XU L Q, et al. iNuc-PseKNC: A sequence-based predictor for predicting nucleosome positioning in genomes with pseudo k-tuple nucleotide composition[J]. Bioinformatics, 2014, 30(11): 1522-1529. DOI:10.1093/bioinformatics/btu083 (  0) 0) |
| [31] |
CHEN W, LIN H, FENG P M, et al. iNuc-PhysChem: A sequence-based predictor for identifying nucleosomes via physicochemical properties[J]. PLoS One, 2012, 7(10): e47843. DOI:10.1371/journal.pone.0047843 (  0) 0) |
| [32] |
LIU H, WU J, XIE J, et al. Characteristics of nucleosome core DNA and their applications in predicting nucleosome positions[J]. Biophysical Journal, 2008, 94(12): 4597-604. DOI:10.1529/biophysj.107.117028 (  0) 0) |
| [33] |
GABDANK I, BARASH D, TRIFONOV E N. Single-base resolution nucleosome mapping on DNA sequences[J]. Journal of biomolecular Structure & Dynamics, 2010, 28(1): 107-121. DOI:10.1080/07391102.2010.10507347 (  0) 0) |
| [34] |
CUI F, CHEN L, LOVERSO P R, et al. Prediction of nucleosome rotational positioning in yeast and human genomes based on sequence-dependent DNA anisotropy[J]. BMC Bioinformatics, 2014, 15(1): 313. DOI:10.1186/1471-2105-15-313 (  0) 0) |
| [35] |
ZHAO X, PEI Z, LIU J, et al. Prediction of nucleosome DNA formation potential and nucleosome positioning using increment of diversity combined with quadratic discriminant analysis[J]. Chromosome Research, 2010, 18(7): 777-785. DOI:10.1007/s10577-010-9160-9 (  0) 0) |
| [36] |
YUAN G C, LIU J S. Genomic sequence is highly predictive of local nucleosome depletion[J]. PLoS Computational Biology, 2008, 4(1): e13. DOI:10.1371/journal.pcbi.0040013 (  0) 0) |
| [37] |
ANSELMI C, BOCCHINFUSO G, DE SANTIS P, et al. Dual role of DNA intrinsic curvature and flexibility in determining nucleosome stability[J]. Journal of Molecular Biology, 1999, 286(5): 1293-1301. DOI:10.1006/jmbi.1998.2575 (  0) 0) |
| [38] |
DE SANTIS P, MOROSETTI S, SCIPIONI A. Prediction of nucleosome positioning in genomes: limits and perspectives of physical and bioinformatic approaches[J]. Journal of Biomolecular Structure & Dynamics, 2010, 27(6): 747-764. DOI:10.1080/07391102.2010.10508583 (  0) 0) |
| [39] |
SEREDA Y V, BISHOP T C. Evaluation of elastic rod models with long range interactions for predicting nucleosome stability[J]. Journal of Biomolecular Structure & Dynamics, 2010, 27(6): 867-887. DOI:10.1080/073911010010524948 (  0) 0) |
| [40] |
LIU G, XING Y, ZHAO H, et al. A deformation energy-based model for predicting nucleosome dyads and occupancy[J]. Scientific Reports, 2016(6): 24133. DOI:10.1038/srep24133 (  0) 0) |
| [41] |
MIELE V, VAILLANT C, D'AUBENTON-CARAFA Y, et al. DNA physical properties determine nucleosome occupancy from yeast to fly[J]. Nucleic Acids Research, 2008, 36(11): 3746-3756. DOI:10.1093/nar/gkn262 (  0) 0) |
| [42] |
TOLSTORUKOV M Y, COLASANTI A V, MCCANDLISH D M, et al. A novel roll-and-slide mechanism of DNA folding in chromatin: Implications for nucleosome positioning[J]. Journal of Molecular Biology, 2007, 371(3): 725-738. DOI:10.1016/j.jmb.2007.05.048 (  0) 0) |
| [43] |
MOROZOV A V, FORTNEY K, GAYKALOVA D A, et al. Using DNA mechanics to predict in vitro nucleosome positions and formation energies[J]. Nucleic Acids Research, 2009, 37(14): 4707-4722. DOI:10.1093/nar/gkp475 (  0) 0) |
| [44] |
CHEN W, FENG P, DING H, et al. Using deformation energy to analyze nucleosome positioning in genomes[J]. Genomics, 2016, 107(2-3): 69-75. DOI:10.1016/j.ygeno.2015.12.005 (  0) 0) |
| [45] |
DENIZ Ö, FLORES O, BATTISTINI F, et al. Physical properties of naked DNA influence nucleosome positioning and correlate with transcription start and termination sites in yeast[J]. BMC Genomics, 2011(12): 489. DOI:10.1186/1471-2164-12-489 (  0) 0) |
| [46] |
ALBERT I, MAVRICH T N, TOMSHO L P, et al. Translational and rotational settings of H2A.Z nucleosomes across the Saccharomyces cerevisiae genome[J]. Nature, 2007, 446(7135): 572-576. DOI:10.1038/nature05632 (  0) 0) |
| [47] |
SMITH S B, FINZI L, BUSTAMANTE C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads[J]. Science, 1992, 258(5085): 1122-1126. DOI:10.1126/science.1439819 (  0) 0) |
| [48] |
BUSTAMANTE C, SMITH S B, LIPHARDT J, et al. Single-molecule studies of DNA mechanics[J]. Current Opinion in Structural Biology, 2000, 10(3): 279-285. DOI:10.1016/S0959-440X(00)00085-3 (  0) 0) |
| [49] |
BUSTAMANTE C, BRYANT Z, SMITH S B. Ten years of tension: Single-molecule DNA mechanics[J]. Nature, 2003, 421(6921): 423-427. DOI:10.1038/nature01405 (  0) 0) |
| [50] |
MERGELL B. Structural and elastic properties of DNA and chromatin[D]. Max-Planck-Institut: Für Polymerforschung, Germany, 2003.
(  0) 0) |
| [51] |
CLOUTIER T E, WIDOM J. DNA twisting flexibility and the formation of sharply looped protein-DNA complexes[J]. Proceedings of the National Academy of Sciences USA, 2005, 102(10): 3645-3650. DOI:10.1073/pnas.0409059102 (  0) 0) |
| [52] |
蒋滢, 陈征宇. 蠕虫状链模型在高分子物理研究中的应用[J]. 物理学报, 2016, 65(17): 178201. JIANG Y, CHEN Z Y. The applications of the wormlike chain model on polymer physics[J]. Acta Physica Sinica, 2016, 65(17): 178201. DOI:10.7498/aps.65.178201 (  0) 0) |
| [53] |
BALAEFF A, MAHADEVAN L, SCHULTEN K. Modeling DNA loops using the theory of elasticity[J]. Physical Review E-Statistical, Nonlinear and Soft Matter Physics, 2006, 73(3 Pt 1): 031919. DOI:10.1103/PhysRevE.73.031919 (  0) 0) |
| [54] |
LIANGRUKSA M, WONGWISES S. An elastic model of DNA under thermal induced stress[J]. Mathematical Biosciences, 2018, 300: 47-54. DOI:10.1016/j.mbs.2018.02.007 (  0) 0) |
| [55] |
SHI Y M, HEARST J E. The Kirchhoff elastic rod, the nonlinear Schrödinger-equation, and DNA supercoiling[J]. Journal of Chemical Physics, 1994, 101: 5186-5200. DOI:10.1063/1.468506 (  0) 0) |
| [56] |
GOYAL S. A dynamic rod model to simulate mechanics of cables and DNA[D]. Michigan: The University of Michigan, USA, 2006.
(  0) 0) |
| [57] |
OLSON W K, BANSAL M, BURLEY S K, et al. A standard reference frame for the description of nucleic acid base-pair geometry[J]. Journal of Molecular Biology, 2001, 313(1): 229-237. DOI:10.1006/jmbi.2001.4987 (  0) 0) |
| [58] |
PETERS J P, MAHER L J. DNA curvature and flexibility in vitro and in vivo[J]. Quarterly Reviews of Biophysics, 2010, 43(1): 23-63. DOI:10.1017/S0033583510000077 (  0) 0) |
| [59] |
LU X J, OLSON W K. 3DNA: A software package for the analysis, rebuilding and visualization of three dimensional nucleic acid structures[J]. Nucleic Acids Research, 2003, 31(17): 5108-5121. DOI:10.1093/nar/gkg680 (  0) 0) |
| [60] |
TSAI L, LUO L, SUN Z. Sequence-dependent flexibility in promoter sequences[J]. Journal of biomolecular Structure & Dynamics, 2002, 20(1): 127-134. DOI:10.1080/07391102.2002.10506828 (  0) 0) |
| [61] |
GOÑI J R, PÉREZ A, TORRENTS D, et al. Determining promoter location based on DNA structure first-principles calculations[J]. Genome Biology, 2007, 8(12): R263. DOI:10.1186/gb-2007-8-12-r263 (  0) 0) |
| [62] |
ZUO Y C, LI Q Z. Identification of TATA and TATA-less promoters in plant genomes by integrating diversity measure, GC-Skew and DNA geometric flexibility[J]. Genomics, 2011, 97(2): 112-120. DOI:10.1016/j.ygeno.2010.11.002 (  0) 0) |
| [63] |
ZUO Y C, ZHANG P, LIU L, et al. Sequence-specific flexibility organization of splicing flanking sequence and prediction of splice sites in the human genome[J]. Chromosome Research, 2014, 22(3): 321-334. DOI:10.1007/s10577-014-9414-z (  0) 0) |
| [64] |
ZHANG B, LIU G. Predicting recombination hotspots in yeast based on DNA sequence and chromatin structure[J]. Curr Bioinformatics, 2014, 9(1): 28-33. DOI:10.2174/1574893608999140109121444 (  0) 0) |
| [65] |
CHEN W, FENG P M, LIN H, et al. iRSpot-PseDNC: Identify recombination spots with pseudo dinucleotide composition[J]. Nucleic Acids Research, 2013, 41(6): e68. DOI:10.1093/nar/gks1450 (  0) 0) |
| [66] |
GO M, GO N. Fluctuations of an alpha-helix[J]. Biopolymers, 1976, 15(6): 1119-1127. DOI:10.1002/bip.1976.360150608 (  0) 0) |
| [67] |
OLSON W K, GORIN A A, LU X J, et al. DNA sequence-dependent deformability deduced from protein-DNA crystal complexes[J]. Proceedings of the National Academy of Sciences USA, 1998, 95(19): 11163-11168. DOI:10.1073/pnas.95.19.11163 (  0) 0) |
| [68] |
PÉREZ A, LANKAS F, LUQUE F J, et al. Towards a molecular dynamics consensus view of B-DNA flexibility[J]. Nucleic Acids Research, 2008, 36(7): 2379-2394. DOI:10.1093/nar/gkn082 (  0) 0) |
| [69] |
BERMAN H M, OLSON W K, BEVERIDGE D L, et al. The nucleic acid database: A comprehensive relational database of three-dimensional structures of nucleic acids[J]. Biophysical Journal, 1992, 63(3): 751-759. DOI:10.1016/S0006-3495(92)81649-1 (  0) 0) |
| [70] |
YUAN G C, LIU Y J, DION M F, et al. Genome-scale identification of nucleosome positions in S. cerevisiae[J]. Science, 2005, 309(5734): 626-630. DOI:10.1126/science.1112178 (  0) 0) |
| [71] |
WANG J Y, WANG J, LIU G. Calculation of nucleosomal DNA deformation energy: Its implication for nucleosome positioning[J]. Chromosome Research, 2012, 20(7): 889-902. DOI:10.1007/s10577-012-9328-6 (  0) 0) |
| [72] |
LIU G, XING Y, ZHAO H, et al. The implication of DNA bending energy for nucleosome positioning and sliding[J]. Scientific Reports, 2018, 8(1): 8853. DOI:10.1038/s41598-018-27247-x (  0) 0) |
| [73] |
LIU G, CUI X, LI H, et al. Evolutionary direction of processed pseudogenes[J]. Science China Life Sciences, 2016, 59(8): 839-849. DOI:10.1007/s11427-016-5074-x (  0) 0) |
| [74] |
LIU Guoqing, FENG Fan, ZHAO Xiujuan, et al. Nucleosome organization around pseudogenes in the human genome[J]. BioMed Research International, 2015, 24(6): 1-7. DOI:10.1155/2015/821596 (  0) 0) |
| [75] |
CHEVEREAU G, PALMEIRA L, THERMES C, et al. Thermodynamics of intra-genic nucleosome ordering[J]. Physical Review Letters, 2009, 103(18): 188103. DOI:10.1103/PhysRevLett.103.188103 (  0) 0) |
| [76] |
LIU Guoqing, LIU Guojun, TAN Jiuxin, et al. DNA physical properties outperform sequence compositional information in classifying nucleosome-enriched and-depleted regions[EB/OL]. Genomics, https://www.onacademic.com/detail/journal_1000040429445010_dd3d.html, 2018. DOI: 10.1016/j.ygeno.2018.07.013.
(  0) 0) |
| [77] |
FATHIZADEH A, BERDY BESYA A, REZA EJTEHADI M, et al. Rigid-body molecular dynamics of DNA inside a nucleosome[J]. The European Physical Journal E, 2013, 36(3): 21. DOI:10.1140/epje/i2013-13021-4 (  0) 0) |
| [78] |
PACKER M J, DAUNCEY M P, HUNTER C A. Sequence-dependent DNA structure: Tetranucleotide conformational maps[J]. Journal of Molecular Biology, 2000, 295(1): 85-103. DOI:10.1006/jmbi.1999.3237 (  0) 0) |
| [79] |
PASI M, MADDOCKS J H, BEVERIDGE D, et al. μABC: A systematic microsecond molecular dynamics study of tetranucleotide sequence effects in B-DNA[J]. Nucleic Acids Research, 2014, 42(19): 12272-12283. DOI:10.1093/nar/gku855 (  0) 0) |
 2019, Vol. 17
2019, Vol. 17

