1971年Dostrovsky和O'Keefe在位于鼠脑海马结构区域中发现了一种具有空间特异性放电特征的神经元细胞-位置细胞[1]。该细胞是鼠脑海马结构中的主要神经元,当大鼠自由运动到环境中的某一特定位置时,相应位置细胞会发生最大化放电活动,将位置细胞发生最大化放电活动所对应区域称为该位置细胞的“位置野”。人类大脑中同样发现了类似于大鼠位置细胞特性的细胞存在[2-3]。随着对位置细胞进一步生理学研究发现,位置细胞放电活动在大鼠面向空间目标导航发挥着关键作用,该细胞放电活动受环境因素影响。因此,研究外部环境对位置细胞放电活动影响, 并将其和啮齿类动物空间导航联系起来具有重要意义。
1 模型生理学依据位置细胞被发现以来,许多学者对该细胞进行了相关研究,由此提出了大量的位置细胞模型,主要包括有基于高斯函数的位置细胞模型[4],基于竞争学习位置细胞模型[5],基于独立成分分析位置细胞模型[6],基于自组织映射位置细胞模型[7]和基于卡尔曼滤波位置细胞模型[8]等。然而,以上所提到的模型并没有将外部线索(如视觉、嗅觉等)对位置细胞放电活动影响考虑在内。因为生理学实验研究发现将视觉线索移除后,位置细胞放电活动会发生强烈变化,位置细胞位置野变得不稳定,这就暗示了视觉线索对于位置细胞位置野的形成和位置野的稳定性具有重要影响[9]。在缺乏视觉线索的情况下,许多研究学者认为路径积分作为一种额外的机制使得大鼠能够在空间环境中自由导航[10]。然而,Save等人的实验表明当大鼠处于黑暗环境中进行自由导航时,单一的路径积分不足以维持位置细胞位置野的稳定性[11]。如果没有额外的视觉线索,随着大鼠自由探索环境,路径积分会导致大鼠在方向和距离上产生很大的累积误差。因此,这就需要通过来自于外部环境中具有稳定位置信息(视觉线索)的参考物来校正从而减小误差[12]。
研究发现,当大鼠在某一空间环境中自由探索该环境空间时,鼠脑海马结构中的各位置细胞会在各自对应的空间位置处发生最大化放点活动,即在各位置处产生相对应的“位置野”[13]。大鼠对空间环境自由探索完成后,在大鼠脑内形成了其对所处空间环境的认知地图,该认知地图是各位置细胞“位置野”联合表征得到的。认知地图表征空间环境,研究发现单凭该认知地图并不能够使大鼠来正确的预测其下一时刻的运动方向,即不能够完成面向空间环境某一目标导航的任务。随着研究不断深入,研究者发现大脑控制中心内侧前额叶皮层(Medial prefrontal cortex, mPFC)与海马之间的动态联系是大鼠正确预测其下一刻运动方向的关键所在[14-15]。大脑前额叶皮层中最主要的神经细胞是运动神经元,该神经元与大鼠的空间运动息息相关[16-17]。鼠脑海马中最主要的神经元细胞是位置细胞。大脑腹侧被盖区(Ventral tegmental area, VTA)里主要存在的神经元细胞是多巴胺能神经元(Dopaminergic neurons)[18-19],该神经元细胞与奖励预测误差信号相关。它能够将接收到的信息传输至伏隔核(Nucleus accumbens, NA)。研究发现大鼠脑海马中的信息主要传输至伏隔核,伏隔核和前额叶皮层之间的信息传递方式是双向纤维投射[20]。即伏隔核从海马接收空间环境信息,从大脑腹侧被盖区接收奖励预测误差信息,通过与前额叶皮层相互作用来正确预测大鼠下一时刻的运动方向。大鼠面向目标的导航任务神经生理学依据是海马位置细胞与伏隔核神经元之间与奖励信号相关的突触调节,伏隔核进一步将信息投射至大鼠前额叶皮层来实现大鼠正确预测下一时刻运动方向。大脑前额叶皮层中主要是运动神经元。海马中主要是位置细胞。基于此,利用位置细胞、运动神经元构建一种前馈神经网络模型,采用Q学习算法来实现大鼠面向目标导航任务。
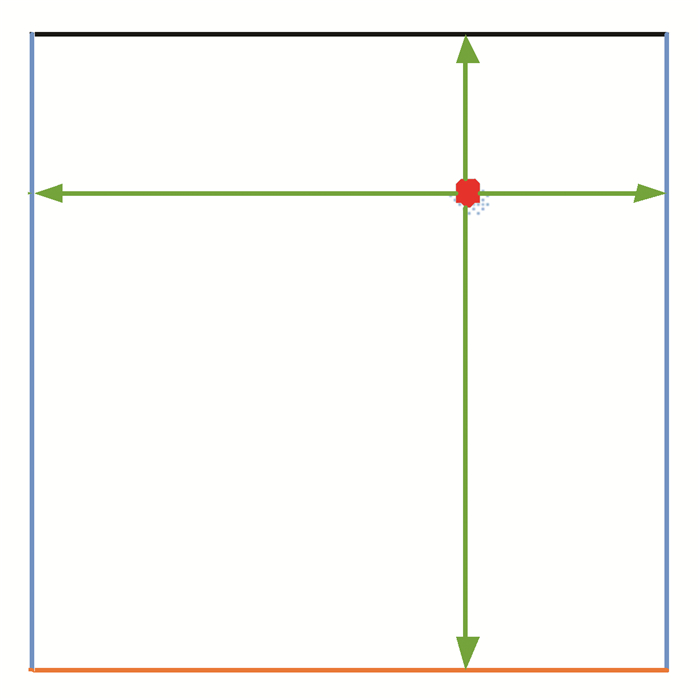
2 方法 2.1 视觉线索感官输入实验环境是一个尺寸为10 000 × 10 000个点所构成的正方形盒子,该正方形盒子面积为1平方米。作为视觉线索,正方形盒子的四个墙面被不同的颜色所标记(如图 1所示)。本文将大鼠所处当前位置距离正方形四个墙面的垂直距离作为大鼠当前的视觉输入信息。图 1中红色小圆点表示的是大鼠当前所处环境中的位置坐标。从该点到四个墙面的垂直距离(如图中的绿色箭头所示)表示的是大鼠所处当前位置的视觉感知输入信息。将视觉输入定义为vx, yk(t),其中x和y表示大鼠所处空间环境当前位置坐标,k(k=1, 2, 3, 4)表示的是四个不同颜色所标记的墙面。在该模型中,假定大鼠在实验环境中任意跑动时只能看到它所处位置正前方的墙面。大鼠离某一不可见墙面的距离等于大鼠上一时刻可见该墙面时的距离。用公式(1)描述:
| $ v_{x,y}^k\left( t \right) = v_{x,y}^k\left( {t - 1} \right) $ | (1) |
|
图 1 实验环境 Figure 1 Experimental environment |
其中k表示的是四个不同颜色所标记的墙面,t表示的是时间。
考虑到实际因素,在视觉感知信息输入中添加一定的噪声信号,假定大鼠在空间环境中自由跑动时对于长距离估计会产生一定的误差。由公式(2)描述:
| $ V_{x,y}^m = \frac{{\left( {0.03\varphi _v^m + 1} \right)v_{x,y}^m}}{l} $ | (2) |
其中,变量φvm是服从[-1, 1]均匀分布的随机值。对视觉输入信息进行规范化其值被限定在[0, 1]区间内,l代表的是环境的边长。
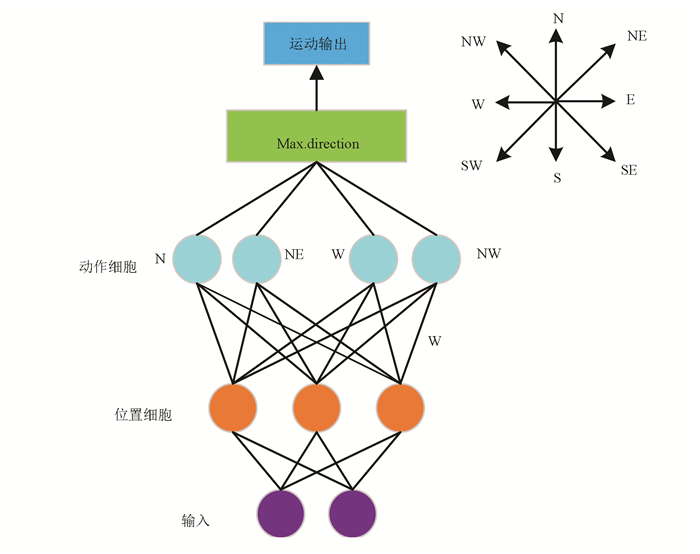
本文中,构建了一个由输入层、位置细胞、运动神经元(动作细胞)和输出层所组成的前馈神经网络模型来实现大鼠面向目标导航任务,前馈神经网络模型如图 2所示。
|
图 2 前馈神经网络模型 Figure 2 Feed-forward neural network model |
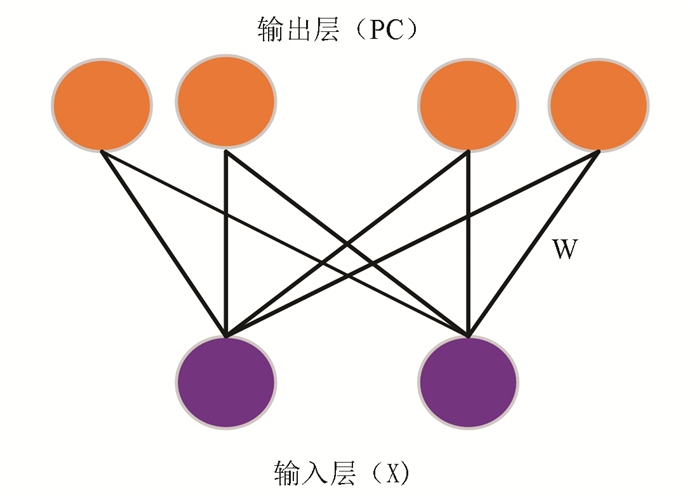
通过构建具有输入层和输出层的前馈神经网络对位置细胞建模。如图 3所示,输入层是视觉输入信息X: Vx, yk。由图 3可知该前馈神经网络输入层的每一个神经元通过连接权重Wi=[wi, 1, wi, 2…wi, 4]与输出层所有位置细胞神经元依次连接。i=1,…,Q,Q=500表示的是前馈神经网络中位置细胞总数。连接权重函数fu由公式(3)来描述。
| $ {f_u} = \left( {1 + {e^{\frac{{u - v}}{{2{\sigma ^2}}}}}} \right) - 1 $ | (3) |
|
图 3 位置细胞模型 Figure 3 Model of place cells |
其中,u是服从[0, 1]之间均匀分布的随机值,v=0.5和σ=0.2。位置细胞放电率见公式(4),随机初始化权值,针对某一特定视觉输入信息通过竞争学习会激活位置细胞。
第i个位置细胞放电率由高斯函数表征[21],由公式(4)来描述:
| $ r_t^i = {{\rm{e}}^{ - \frac{{{{\left[ {\frac{1}{4}\left\| {{X_t} - W_t^i} \right\|} \right]}^2}}}{{2\sigma _f^2}}}} $ | (4) |
其中,σf=0.07表示的是位置细胞位置野宽度。前馈神经网络模型中权重值调整依据胜者为王机制。即针对某一特定视觉输入信息,获胜的位置细胞神经元χt与该特定视觉输入信息之间权重值会进行相应调整,其余权重值不变。基于竞争学习获胜的位置细胞神经元χt用公式(5)来描述:
| $ {\chi _t} = \arg {\min _i}\left\| {{X_t} - W_t^i} \right\| $ | (5) |
获胜神经元权重值按照公式(6)改变:
| $ W_{t + 1}^{{\chi _t}} = W_t^{{\chi _t}} + \alpha \left( {{X_t} - W_t^{{\chi _t}}} \right) $ | (6) |
其中,0 < α < < 1代表的是学习效率因子。
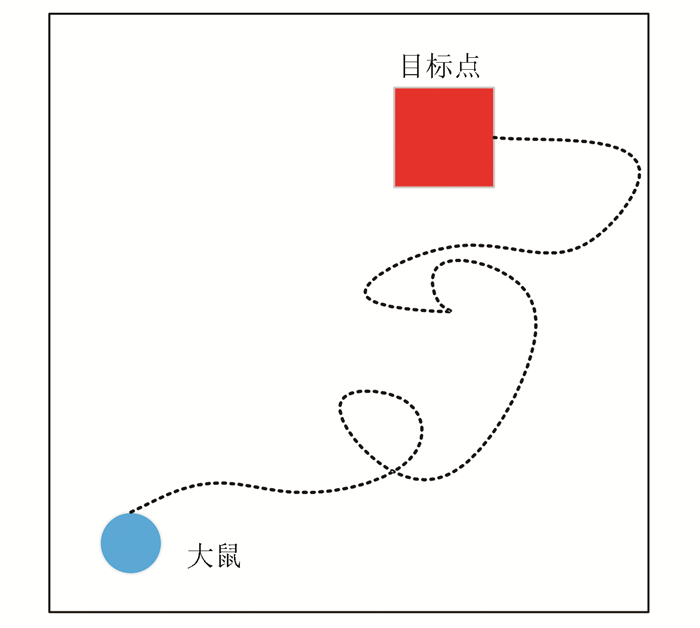
2.3 目标导航任务某一特定视觉输入信息通过竞争学习算法激活某些位置细胞神经元,激活位置细胞神经元与运动神经元通过Q学习算法可以得到大鼠下一时刻的运动方向。大鼠在空间环境中不断学习直至能找到任一起始位置到目标位置之间导航的最短路径为止,大鼠空间导航示意如图 4所示。使用如图 1所示的实验环境,该实验环境的四面墙被不同颜色(黑色、紫色、红色和蓝色)所标记。大鼠运动的起始位置如图 4中蓝色圆点标记所示。目标点位置如图 4中红色正方形所示。当大鼠刚进入到实验环境中时,它是在随机探索环境的过程中找到目标位置(如图 4中黑色虚线所示)。当大鼠经过长时间的学习后,就能够快速实现起始位置到目标位置的最短路径导航。
|
图 4 大鼠空间导航示意图 Figure 4 Schematic diagram of spatial navigation in rat's brain 注:彩图见电子版:http://swxxx.alljournals.cn/ch/index.aspx.(2019年第1期). |
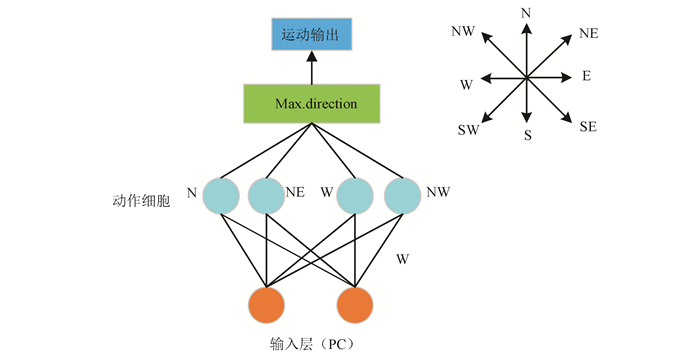
本文中使用Q学习算法对大鼠空间导航进行研究。该算法应用在如图 5所示的两层前馈神经网络模型中,位置细胞作为两层前馈神经网络的输入层,分别与8个运动神经元连接(该8个运动神经元分别代表 8个不同方向(北(N),东北(NE),东(E),东南(SE),南(S),西南(SE),西(W),西北(NW))。通过Q学习算法计算得到以上8个方向的Q值,Q值最大的方向就是大鼠下一时刻的运动方向。大鼠向正西和正东的运动由公式(7)和(8)来描述:
| $ \mathit\Delta x = \pm \left( {\mathit\Delta s + c \cdot {\psi _x}} \right) $ | (7) |
| $ \mathit\Delta y = c \cdot {\psi _y} $ | (8) |
|
图 5 由输入层(位置细胞)、运动神经元构建的前馈网络模型示意图 Figure 5 Feed-forward network model of the input layer (place cells) and motor neurons |
其中,Δs=500表示的是大鼠步幅大小,ψx和ψy是服从[-1, 1]均匀分布的随机值,c=100表示的是噪声幅值。负号代表大鼠向正西运动,正号代表大鼠向正东运动。同样的,大鼠在西南和东北方向的运动由公式(9)和(10)来描述:
| $ \mathit\Delta x = \pm \left( {\frac{{\mathit\Delta s}}{{\sqrt 2 }} + c \cdot {\psi _x}} \right) $ | (9) |
| $ \mathit\Delta y = \pm \left( {\frac{{\mathit\Delta s}}{{\sqrt 2 }} + c \cdot {\psi _x}} \right) $ | (10) |
当大鼠随机探索空间环境的过程中运动到某一位置时计算所得Q值是0时,大鼠在当前位置下一时刻的运动方向是不确定,它在当前位置保持方向不变的概率为1-pk,在当前位置选择一个新方向运动的概率为pk=0.25。当计算的Q值不为0时,大鼠的下一时刻的运动方向由Q值来确定的。
位置细胞到动作细胞学习机制是Q学习算法。简便起见,将t时刻第i个位置细胞放电率由公式(11)来描述:
| $ {\Psi _i}\left( {{r_t}} \right) = \left\{ \begin{array}{l} 1\;{\rm{if}}\;r_t^i > 0.5\\ 0\;{\rm{other}}\;{\rm{wise}} \end{array} \right. $ | (11) |
其中,i=1,…,Q,Q=500表示的是神经网络模型中位置细胞总数。
由公式(12)来定义动作值函数:
| $ Q\left( {{r_t},{a_t}} \right) = \frac{{{\Sigma _i}{\Gamma _{i,{a_t}}}{\Psi _i}\left( {{r_t}} \right)}}{{{\Sigma _i}{\Psi _i}\left( {{r_t}} \right)}} $ | (12) |
其中,Γi, a表示的是第i个位置细胞与运动神经元a之间的连接权重值。根据Reynolds所提及的使用平均Q学习规则[22]。即按照公式(13)更新t时刻真正产生动作at的权值Γi, at。
| $ {\mathit{\Gamma }_{i,{a_t}}} = {\mathit{\Gamma }_{i,{a_t}}} + \beta \left( {\delta {{\max }_a}A\left( {{r_{t + 1}},{a_{t + 1}}} \right) + {R_{t + 1}} - {\mathit{\Gamma }_{i,{a_t}}}} \right){\Psi _i}\left( {{r_t}} \right) $ | (13) |
其中,β=0.7表示的是学习率,δ=0.7表示的是折减系数,R表示的是奖励。将奖励函数Rt由函数(14)来描述:
| $ {R_t} = \left\{ \begin{array}{l} 1\;{\rm{if}}\;{\rm{the}}\;{\rm{rat}}\;{\rm{has}}\;{\rm{found}}\;{\rm{the}}\;{\rm{goal}}\\ 0\;{\rm{other}}{\rm{wise}}. \end{array} \right. $ | (14) |
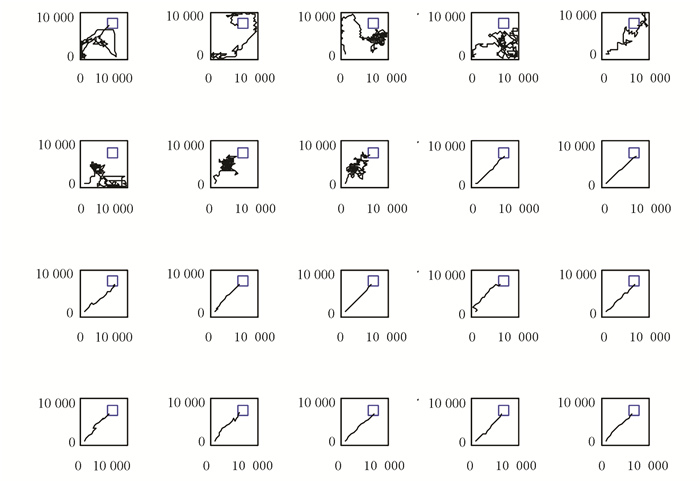
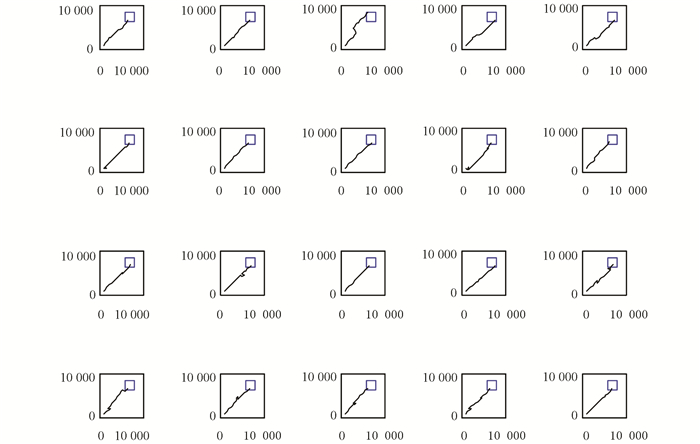
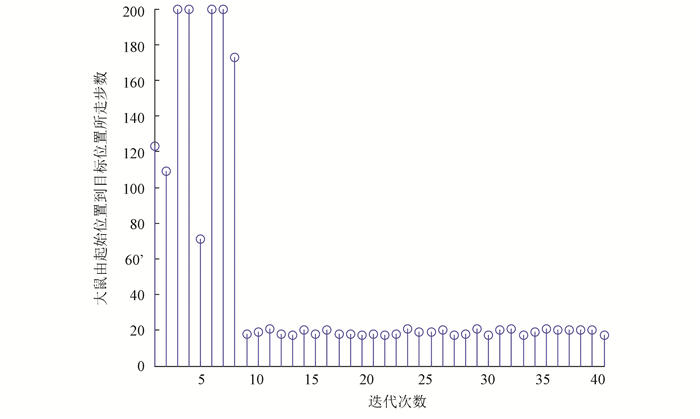
实验过程是大鼠刚进入到实验环境中时,它是在随机探索环境的过程中找到目标位置。当大鼠经过长时间的学习后,就能够快速实现起始位置到目标位置的最优路径导航,实验结果如图 6、图 7、图 8和表 1所示。本次实验中大鼠一共进行了40轮实验。图 6是前20轮实验结果示意图,图 7是后20轮实验结果示意图。由图 6和图 7可以很直观的看出在前8轮实验中大鼠由于刚进入到一个比较陌生的环境中,它只能随机的去探索目标位置,其运动轨迹是随机的,当它经过一段的时间学习后对其所处空间环境有了学习认知,便能够从第9轮实验开始找到从起始位置到目标位置的最优路径。图 8是40轮实验过程中每轮实验大鼠到达目标位置所需步数示意图,由该图也能很直观的看出从第9轮实验开始大鼠能够找到从起始位置到目标位置的最优路径。表 1是大鼠基于Q学习面向目标导航迭代次数与到达目标位置所需步数对应关系表。由该表能够直观的看出前8轮实验中由于大鼠随机探索环境,此时它到达目标位置所走步数是随机的没有规律可循的,当经过一段时间学习后,它到达目标位置的步数是基本稳定的,由表 1可知从第9轮实验开始,大鼠到达目标位置所走步数大约为20步。
|
图 6 大鼠前20次运行轨迹 Figure 6 Trajectories of the rat's paths from the first 20 runs |
|
图 7 大鼠后20次运行轨迹 Figure 7 Trajectories of the rat's paths from the last 20 runs |
|
图 8 大鼠到达目标位置所需步数示意图 Figure 8 The number of steps needed to reach the target position for the rat |
| 表 1 大鼠基于Q学习面向目标导航迭代次数与到达目标位置所需步数对应关系 Table 1 Corelation between the number of iterations of the good-oriented navigation based on Q learning and the number of steps needed to reach the target position |
强化学习算法主要是应用于解决学习类任务当中,针对仿生学上又主要分为两类,一类是用于鼠脑海马仿生导航中[23-26],另一类是仿生机器人在某一特定空间环境中通过强化学习来认知所处空间环境,进而与环境交互执行相关动作[27-30]。本研究充分表明了基于位置细胞、运动神经元来构建一种前馈神经网络模型,采用Q学习算法能够快速实现大鼠面向目标导航任务。
| [1] |
O'KEEFE J, DOSTROVSKY J. The hippocampus as a spatial map.Preliminary evidence from unit activity in the freely-moving rat[J]. Brain Research, 1971, 34(1): 171-175. DOI:10.1016/0006-8993(71)90358-1 (  0) 0) |
| [2] |
EKSTROM A D, KAHANA M J, CAPLAN J B, et al. Cellular networks underlying human spatial navigation[J]. Nature, 2003, 425(6954): 184-188. DOI:10.1038/nature01964 (  0) 0) |
| [3] |
林龙年. 发现大脑定位系统的细胞组构[J]. 科学(上海), 2015, 67(1): 30-34. LIN Longnian. Cellular structure of the brain localization system[J]. Science (Shanghai), 2015, 67(1): 30-34. DOI:10.3969/j.issn.0368-6396.2015.01.009 (  0) 0) |
| [4] |
TOURETZKY D S, REDISH A D. Theory of rodent navigation based on interacting representations of space[J]. Hippocampus, 1996, 6(3): 247-270. DOI:10.1002/(SICI)1098-1063(1996)6:3<247::AID-HIPO4>3.0.CO;2-K (  0) 0) |
| [5] |
SHARP P E. Computer simulation of hippocampal place cells[J]. Psychobiology, 1991, 19(2): 103-115. DOI:10.3758/BF03327179 (  0) 0) |
| [6] |
TAKACS B, ANDRAS L R. Independent component analysis forms place cells in realistic robot simulations[J]. Neurocomputing, 2006, 69(10-12): 1249-1252. DOI:10.1016/j.neucom.2005.12.086 (  0) 0) |
| [7] |
CHOKSHI K, WERMTER S, WEBER C. Learning localisation based on landmarks using self-organisation[J]. Lecture Notes in Computer Science, 2003, 2714: 504-514. DOI:10.1007/3-540-44989-2_60 (  0) 0) |
| [8] |
BOUSQUET O, BALAKRISHNAN K, HONAVAR V. Is the hippocampus a Kalman filter?[J]. Pacific Symposium on Biocomputing Pacific Symposium on Biocomputing, 1998(1): 657-668. (  0) 0) |
| [9] |
MARKUS E J, BARNES C A, MCNAUGHTON B L, et al. Spatial information content and reliability of hippocampal CA1 neurons:effects of visual input[J]. Hippocampus, 1994, 4(4): 410-421. DOI:10.1002/hipo.450040404 (  0) 0) |
| [10] |
ETIENNE A S, JEFFERY K J. Path integration in mammals[J]. Hippocampus, 2004, 14(2): 180-192. DOI:10.1002/hipo.10173 (  0) 0) |
| [11] |
SAVE E, NERAD L, POUCET B. Contribution of multiple sensory information to place field stability in hippocampal place cells[J]. Hippocampus, 2000, 10(1): 64-76. DOI:10.1002/(SICI)1098-1063(2000)10:1<64::AID-HIPO7>3.0.CO;2-Y (  0) 0) |
| [12] |
MAASWINKEL H, WHISHAW I Q. Homing with locale, taxon, and dead reckoning strategies by foraging rats:sensory hierarchy in spatial navigation[J]. Behavioural Brain Research, 1999, 99(2): 143-152. DOI:10.1016/S0166-4328(98)00100-4 (  0) 0) |
| [13] |
JEFFERY K J, HAYMAN R. Plasticity of the hippocampal place cell representation[J]. Reviews in the Neurosciences, 2004, 15(5): 309-331. DOI:10.1515/REVNEURO.2004.15.5.309 (  0) 0) |
| [14] |
马晓宇, 林龙年. 解码大脑的空间方位认知[J]. 生命科学, 2014(12): 1248-1254. MA Xiaoyu, LIN Longnian. Decoding the spatial orientation of the brain[J]. Chinese Bulletin Life Sciences, 2014(12): 1248-1254. (  0) 0) |
| [15] |
DRAGOI G, TONEGAWA S. Preplay of future place cell sequences by hippocampal cellular assemblies[J]. Nature, 2011, 469(7330): 397-403. DOI:10.1038/nature09633 (  0) 0) |
| [16] |
RODRIGO A H, DOMENICO S I D, AYAZ H, et al. Differentiating functions of the lateral and medial prefrontal cortex in motor response inhibition[J]. Neuroimage, 2014, 85(2): 423-431. DOI:10.1016/j.neuroimage.2013.01.059 (  0) 0) |
| [17] |
KULA J, BLASIAK A, CZERW A, et al. Short-term repeated corticosterone administration enhances glutamatergic but not GABAergic transmission in the rat motor cortex[J]. Pflügers Archiv-European Journal of Physiology, 2016, 468(4): 679-691. DOI:10.1007/s00424-015-1773-6 (  0) 0) |
| [18] |
SCHULTZ W, DAYAN P, MONTAGUE P R. A neural substrate of prediction and reward[J]. Science, 1997, 275(5306): 1593-1599. DOI:10.1126/science.275.5306.1593 (  0) 0) |
| [19] |
SCHULTZ W. Predictive reward signal of dopamine neurons[J]. Journal of Neurophysiology, 2010, 80(1): 1-27. DOI:10.1152/jn.1998.80.1.1 (  0) 0) |
| [20] |
SESACK S R, PICKEL V M. In the rat medial nucleus accumbens, hippocampal and catecholaminergic terminals converge on spiny neurons and are in apposition to each other[J]. Brain Research, 1990, 527(2): 266-279. DOI:10.1016/0006-8993(90)91146-8 (  0) 0) |
| [21] |
O'KEEFE J, BURGESS N. Geometric determinants of the place fields of hippocampal neurons[J]. Nature, 1996, 381(6581): 425-428. DOI:10.1038/381425a0 (  0) 0) |
| [22] |
REYNOLDS S I. The stability of general discounted reinforcement learning with linear function approximation[J]. In Proceedings of the UK Workshop on Computational Intelligence (UKCI-02), 2002(1): 139-146. (  0) 0) |
| [23] |
YU N G, YUAN Y H, LI T, et al. A cognitive map building algorithm by means of cognitive mechanism of hippocampus[J]. Acta Automatica Sinica, 2018, 44(1): 52-73. (  0) 0) |
| [24] |
YU N G, FANG L.A computational model for the formation of grid field based on path integration[C].IEEE: 28th Chinese Control and Decision Conference, 2016, 5581-5586.DOI: 10.1109/CCDC.2016.7531995.
(  0) 0) |
| [25] |
于乃功, 李倜, 方略. 基于直接强化学习的面向目标的仿生导航模型[J]. 中国科学:信息科学, 2016, 46(3): 325-337. YU Naigong, LI Ti, FANG Lue. Target-oriented bionic navigation model based on direct reinforcement learning[J]. Scientia Sinica Informationis, 2016, 46(3): 325-337. DOI:10.1360/N112015-00217 (  0) 0) |
| [26] |
于乃功, 王琛, 默凡凡. 基于Q学习算法和遗传算法的动态环境路径规划[J]. 北京工业大学学报, 2017, 43(7): 1009-1016. YU Naigong, WANG Chen, MO Fanfan. Dynamic environment path planning based on Q-learning algorithm and genetic algorithm[J]. Journal of Beijing University of Technology, 2017, 43(7): 1009-1016. DOI:10.11936/bjutxb2016120005 (  0) 0) |
| [27] |
赵辉, 赵玉峰. 一种改进的多智能体Q学习算法[J]. 自动化与仪器仪表, 2017(4): 25-27. ZHAO Hui, ZHAO Yufeng. An improved multi-agent Q-learning algorithm[J]. Automation and Instrumentation, 2017(4): 25-27. DOI:10.14016/j.cnki.1001-9227.2017.04.025 (  0) 0) |
| [28] |
柳杨, 王博文, 韩建晖. 移动机器人室内场景主动识别的强化学习方法[J]. 河北工业大学学报, 2018, 47(1): 8-18. LIU Yang, WANG Bowen, HAN Jianhui. Reinforcement learning method for active recognition of indoor scenes of mobile robots[J]. Journal of Hebei University of Technology, 2018, 47(1): 8-18. DOI:10.14081/j.cnki.hgdxb.2018.01.002 (  0) 0) |
| [29] |
庄夏. 基于时延Q学习的机器人动态规划方法[J]. 计算机科学与应用, 2017, 7(7): 671-677. ZHUANG Xia. Dynamic planning method based on time delayed Q-learning[J]. Computer Science and Application, 2017, 7(7): 671-677. DOI:10.12677/CSA.2017.77078 (  0) 0) |
| [30] |
毛自民. RBF网络Q-学习在水下机器人首向角锁定中的应用[J]. 舰船科学技术, 2017, 39(3A): 111-113. MAO Zimin. Application of Q-Learning of RBF network in underwater robot heading angle lock[J]. Ship Science and Technology, 2017, 39(3A): 111-113. DOI:10.3404/j.issn.1672-7619.2017.3A.038 (  0) 0) |
 2019, Vol. 17
2019, Vol. 17

