蛋白质是生命活动的重要承担者,其空间结构在很大程度上决定了它所具有的生物学功能,因此蛋白质结构的预测对于理解蛋白质的结构与功能之间的关系,并在此基础上进行蛋白质复性、突变体设计以及基于结构的药物设计有着极其重要的意义[1]。蛋白质分子是由二十多种氨基酸通过共价键连接而成的肽链形成,这些肽链是依据什么原则形成具有一定空间结构的蛋白质分子,仍然是目前没有解决的生物学问题[2]。随着基因组测序工作的完成,生物学研究领域迫切需要找到一种从氨基酸序列出发,以此来预测蛋白质结构和功能的方法。在进行蛋白质结构预测过程中,研究者提出了许多模型,最简单的是Dill等人提出的HP格点模型[3-4], 该模型将所有的氨基酸分为亲水性(H)氨基酸和疏水性(P)氨基酸两类,不考虑侧链的影响,于是氨基酸序列被定义为一个由H和P组成的序列,这个序列遵循自回避原则,可以显示在网格上。蛋白质的天然构象是吉布斯自由能最低的构象是解决蛋白质结构预测问题的基础。截止到现在,已经有许多近似算法应用在HP模型中,如粒子群算法[5-6]、神经网络算法[7]、遗传算法[8-9]等, 这些算法各有各的优缺点,但至今还未发现一种算法完全好于其它算法。HP模型是一个偏理想化的模型,它需要将氨基酸链限制在正方形或矩形区域中,并且最大限度的将所有氨基酸只分为亲水氨基酸和疏水氨基酸,但是有十几种氨基酸并不能够明确区分其疏水性及亲水性,因此凭借HP模型来预测蛋白质结构并不符合实际。
疏水氨基酸相互作用,共价键和范德华力等会影响蛋白质结构的稳定性,自然状态下的蛋白质有一个很紧凑的内部结构,范德华力在短程效应中扮演着一个不可替代的角色,由范德华力方程式所产生的能量越大,蛋白质结构将会越紧凑。因此可以考虑基于范德华力势能解决蛋白质结构的预测问题。
遗传算法(Genetic Algorithm, GA)是由美国密西根大学的Holland教授和他的学生在20世纪60年代创立的[10],该算法以遗传机理和自然进化为基础,模拟了自然界中发生的自适应现象,该算法被创立之后就被广泛引用到工程问题中,现在已经发展成为一种“自适应启发式概率性迭代式全局搜索算法”。目前,已被广泛应用到功能优化、神经网络、机器学习、模式识别以及图像处理[11]等领域。
本文剩余部分按如下安排:第二章中我们介绍了范德华力势能预测蛋白质结构问题的数学模型,第三章中介绍了基本遗传算法以及定义了调整策略,第四章中执行数值实验并对结果进行分析,最后在第五章中对整篇论文做了总结并对未来的研究做了展望。
1 数学模型范德华力是分子间作用力,是由分子(原子)间相互接近造成的极化耦合引起的。范德华力势能可由Lennard-Jones势能函数如下表示:
| $ E = \sum\limits_{i \ne j} {{\varepsilon _{ij}}\left[ {\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)12 - 2\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)6} \right]} $ |
其中,
对于蛋白质结构折叠问题,给出一个氨基酸序列,它被抽象为一个C原子链, 氨基酸之间通过范德华力相互作用。本文中,只考虑基于范德华力的蛋白质结构折叠。我们知道范德华力产生的势能越大,蛋白质结构就越紧凑,也即最大范德华势能对应的结构是最优蛋白质构象。
为了能找到稳定的蛋白质结构,基于范德华势能的蛋白质结构预测问题将会转化为数学问题。因为相邻的两个氨基酸之间的距离不是零,所以任意两个原子之间的范德华力势能可由L-J势能方程计算得出。于是,本问题的数学模型按如下表示:
| $ {\text{max}}E = \sum\limits_{i \ne j} {{\varepsilon _{ij}}\left[ {\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)12 - 2\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)6} \right]} \;{\text{s}}{\text{.t}}{\text{.}}{r_{ij}} \ne 0 $ |
化为标准形式:
| $ {\text{min}}E = \sum\limits_{i \ne j} {{\varepsilon _{ij}}\left[ {\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)12 - 2\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)6} \right]} \;{\text{s}}{\text{.t}}{\text{.}}{r_{ij}} \ne 0 $ |
氨基酸序列被抽象为C原子链,查阅文献[12]得知εi=0.12 kcal/mol,rmin= 0.21 nm,同时,我们规定在链上相邻的两个氨基酸之间的距离rij=0.52 nm。
模型中约束条件意味着任意两个氨基酸之间的距离不是零,也即任何两个氨基酸不会处于同一个位置并且只有一个氨基酸能占有该位置。现在,一个生物问题转化成了数学优化问题,并且范德华力势能抛弃了HP模型的局限性,能够更真实的反映出蛋白质的空间结构。
2 遗传算法遗传算法(Genetic Algorithm, GA)最初是由美国的Holland教授提出的模拟自然界中生物进化机制的一种算法,它把达尔文进化论和孟德尔遗传学说作为基础,仿照生物的进化与遗传过程,遵循适者生存和优胜劣汰的规则,通过复制、交叉和变异等一系列操作,将需要解决的问题从初始解逐代逼近最优解。
2.1 调整算子氨基酸序列经过交叉、变异操作后,后代可能会出现循环状态,即相同的位置同时被两个氨基酸占据。为了克服这个缺点,我们构造了调整算子。
由于对氨基酸序列的编码代表了方向,所以先根据初始点与编码将每一个氨基酸的坐标确定下来,接着从序列中第一个氨基酸开始检验,若遇到序列中重复的氨基酸,则从当前重复的氨基酸开始,向后调整直到最后一个点的无重复坐标确定。
在进行调整操作的过程中,可能会碰到一个点的所有方向都不可以取的情况,在数值实验时,就要定义一个记忆函数,每一个氨基酸都会对应一个集合,这个集合记录了这个氨基酸除了当前方向还可以改变的其它方向。如果有一个氨基酸所有方向都会造成重叠,就要返回上一个氨基酸,当前方向不可行,改变上一个氨基酸的方向,并且改变对应的集合。同时,其它方向也不是随意选取的,选取时是存在优先级的。由于和初始点距离越近,氨基酸的序列就会更紧致,所以首先取其它所有可行方向中,对应坐标和初始点的距离最近的方向,最后得到不会发生重叠的序列。
2.2 改进遗传算法的步骤对于预测蛋白质结构的优化问题,改进的遗传算法按照如下步骤进行:
Step 1 随机编码产生初始种群。本文编码方式为:将“沿x轴正方向”设置为1,“与x轴正方向成120°”设置为2,“与x轴正方向成240°”设置为3。种群中随机设置五个个体(氨基酸序列),检验每个氨基酸序列的有效性,如果是不合理序列,就要通过调整算子把它变为合理的序列,计算每个序列的适应度,规定适应度为每个序列的范德华势能。
Step 2 选择。采用轮盘赌选择,进行交叉的个体被选择的概率与它的范德华势能成正比,进行变异的个体被选择的概率与它的范德华势能成反比:
| $ {P_i} = \frac{{{E_i}}}{{\sum\limits_{j = 1}^n {{E_j}} }} $ |
在本文中,每次循环选择三个准备进行交叉的个体,选择两个准备进行变异的序列,于是,交叉如果能够进行就会产生六个新个体,变异能够进行则会产生两个新个体。
Step 3 交叉。采用单点交叉,确定交叉概率pc=0.8, 之后产生一个随机概率r,且0 < r < 1。如果r < pc,则执行交叉操作,对被选择进行交叉的三个个体,随机一个交叉点位,每两个个体的前后两部分相互交换形成新的个体,完成交叉后产生六个新个体。在前面已经指出,氨基酸的位置不能重叠,所以进行交叉后要检验新个体的合理性,如果合理则进行接下来的操作,不合理则要通过调整算子来调整使新的个体能够符合约束条件,然后再继续进行。
Step 4 变异。采用均匀变异,设置变异概率pm=0.05,之后产生一个随机概率,如果随机概率小于变异概率,则执行变异操作,即对被选择进行变异的两个个体,随机一个变异位点,只改变这一个位点的编码,变异规则按照如下方式:1→2, 2→3, 3→1,生成两个新个体。和交叉操作一样,为了防止新生成的个体不符合规则,也要对新生成的个体进行检验,不合理则调用调整算子,合理则继续。
Step 5 适应度评价。一次循环下来,通常都会产生新个体,计算新产生个体的范德华力势能。
Step 6 种群更新。将新生成的个体的适应度与父代进行比较,如果子代个体中有个体的适应度大于父代的适应度,保存子代的最优个体,淘汰父代中差的个体,总之要始终保持种群中有五个个体,在迭代过程中不断更新种群。
Step 7 重复步骤Step 1~Step 6,一直循环到5 000代,最后得到最优解。
由于在遗传算法的过程中,可能会出现局部最优解的情况出现,所以为了克服这个缺陷,在进行数值实验的过程中要重复进行五次以上的实验取最优解。
3 数值模拟为了验证模型和改进算法的有效性,进行数值实验,分别预测氨基酸序列长度为15,17,20,25,30,35的蛋白质结构。
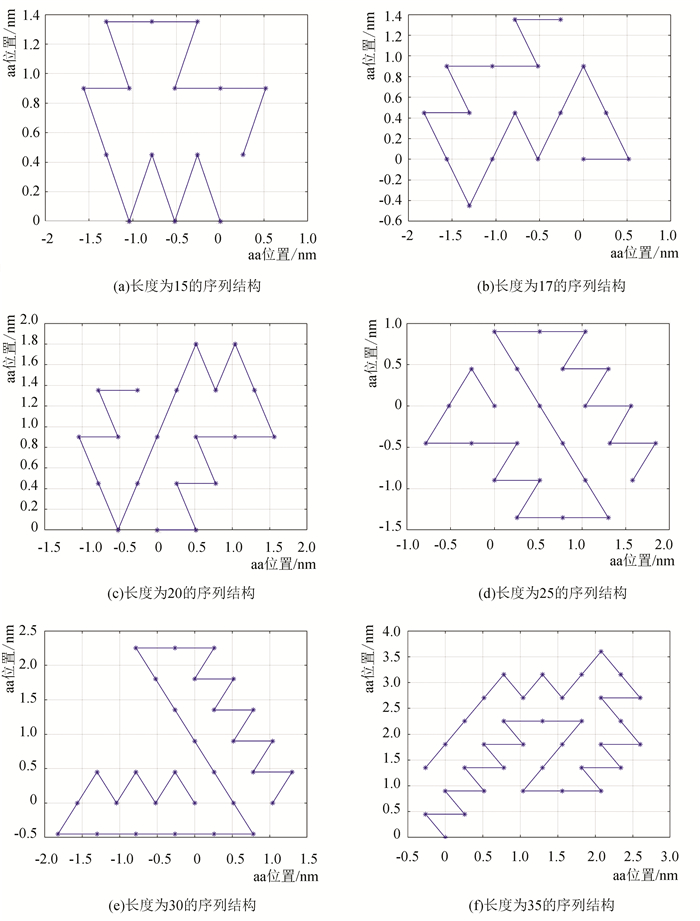
3.1 实验结果在进行数值实验时,对于不同长度的氨基酸序列,我们都重复预测了五次,比较得出一个范德华势能最大的构象,结果见图 1所示。
|
图 1 不同长度的氨基酸序列的二维拆叠构象 Figure 1 Amino acid sequences with different lengths |
进行数值实验时,累加五次实验所得构象的范德华势能,求出平均势能,同时记录不同长度序列计算每代的运行时间以及得到最优解时平均运行时间,结果分别如表 1和表 2所示。
| 表 1 不同长度序列对应的范德华势能 Table 1 Van der Waals potential energy corresponding to sequences of different lengths |
| 表 2 不同长度序列对应的运行时间 Table 2 Running time corresponding to sequences of different lengths |
从表 1中可以看出,平均势能与最大范德华势能的误差比较小,完全在可接受的范围内,这也反映出改进后的遗传算法的有效性。观察表 1和表 2中的数据,我们推测:(1)序列越长,运行时间会越长。(2)范德华势能随着序列长度的增加而增大。(3)应用本文的方法,可以在可接受的时间里得到较长的序列的构象。(4)蛋白质的构象越紧致,结构会更稳定。
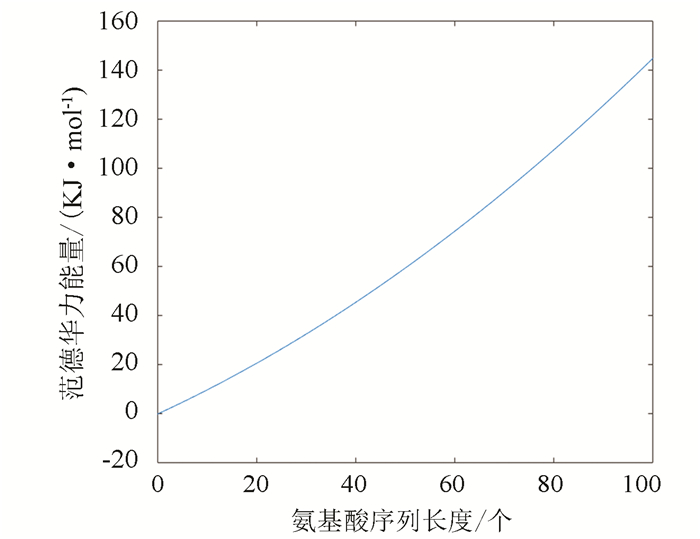
3.2 最大范德华势能拟合函数及误差分析通过观察表 1中范德华势能与序列长度的数据,拟合得出能量与序列长度的关系函数及其函数图像(见图 2):
|
图 2 能量与长度的关系 Figure 2 Relationship between energy and length |
| $ y = 0.0052{x^2} + 0.9285x - 0.0678 $ |
其中,x表示氨基酸序列长度,y表示对应的范德华势能。
分别用拟合函数和改进遗传算法计算了表 1中序列的最大范德华势能,比较结果如表 3所示:
| 表 3 拟合能量和实际能量的比较 Table 3 Comparison of fitting energy and actual energy |
从表 3的误差来看,拟合的效果非常接近程序的结果,这说明拟合函数是可以接受的。于是我们采用拟合函数分别预测序列长度为500, 1 000和2 000的氨基酸序列的最大范德华势能,结果见表 4。
| 表 4 能量拟合函数的预测结果 Table 4 Prediction results of energy fitting function |
从表 4中获知,当氨基酸序列长度是500时,最大范德华力势能是1764.2 kJ·mol-1;当序列长度是1 000时,最大范德华势能是6128.4 kJ·mol-1;当序列长度是2 000时,最大范德华势能是22 657 kJ·mol-1。我们发现,随着氨基酸序列变长,其最大范德华势能也会增大,证实了之前的猜测。
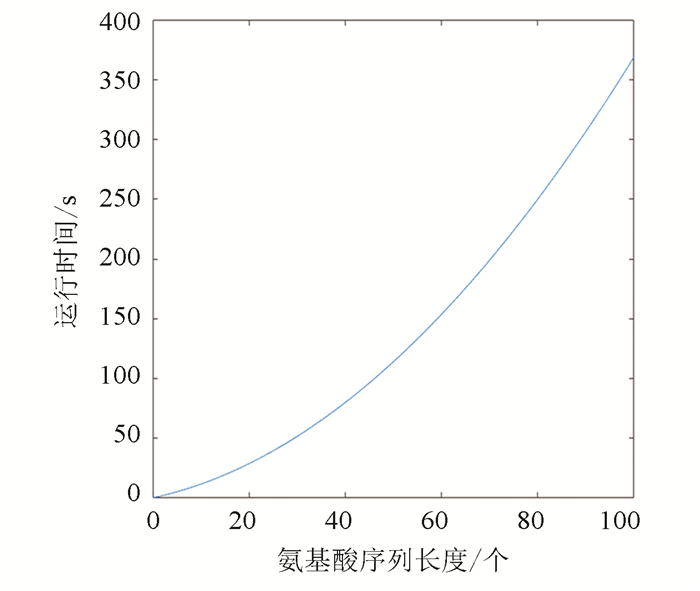
3.3 时间与长度拟合函数及误差分析我们通过观察表 2中程序总运行时间和序列长度的数据,可以拟合得出运行时间和序列长度的函数及其函数图像(见图 3):
|
图 3 运行时间与长度关系 Figure 3 Relationship between running time and length |
| $ y = 0.0282{x^2} + 0.8656x + 0.2150 $ |
其中,x表示序列长度,y表示总运行时间。
分别用拟合函数和改进遗传算法计算了长度为20和30的序列的运行时间,比较结果如表 5。
| 表 5 拟合时间和程序运行时间比较 Table 5 Comparison of fitting time and program running time |
从表 5的误差和误差率来看,拟合的效果非常接近程序的结果,这说明拟合函数是可以接受的,于是我们采用该拟合函数预测序列长度为500, 1 000和2 000的氨基酸序列的平均运行时间,结果见表 6。
| 表 6 时间拟合函数的预测结果 Table 6 Prediction results of time fitting function |
当序列长度是500时,平均运行时间大约是2.1 h;当序列长度是1 000时,平均运行时间是8.1 h;当序列长度是2 000时,平均运行时间是31.8 h。此结果说明基于范德华势能预测蛋白质结构是可行的。
通过对实验数据的分析可以看到,基于范德华势能的数学模型,通过改进的遗传算法来预测蛋白质的空间结构具有很大的可行性,最后得到的氨基酸序列的构象是很紧凑的,因此是比较符合真实结构的。
4 总结与展望本文讨论了基于范德华力的蛋白质结构预测问题。选择范德华势能作为数学优化模型,变量是任意两个C原子之间的距离。目标函数要求范德华势能最大,约束条件是两个氨基酸不占据同一个位置。选择遗传算法来解决此数学模型,并且对遗传算法做了改进。为了防止氨基酸的位置重叠,引入了调整算子的概念,使氨基酸序列最大程度的符合其真实的生物学特性。在数值实验中,改进的遗传算法搜索能力和搜索效率都得到了提高,证明了模型和算法的可行性和有效性。
在未来有很多方向可以追求。首先,本文研究的是二维平面上蛋白质结构预测问题,而真实的蛋白质结构是三维的,在以后的研究中可以考虑将模型和改进的算法扩展到空间蛋白质预测问题中去。其次,可以将模拟的结果与真实的蛋白质结构进行比较,检测模型和算法的有效性。第三,还可以比较蛋白质结构预测的疏水亲水模型和范德华势能模型的结果,分析出各自的优缺点。
总而言之,本文的模型和方法为蛋白质结构预测问题提供了相当大的潜力。
| [1] |
王菲露, 宋杰, 宋杨. BP神经网络在蛋白质二级结构预测中的应用[J]. 计算机技术与发展, 2009, 19(5): 217-219. WANG Feilu, SONG Jie, SONG Yang. Application of BP neural network in protein secondary structure prediction[J]. Computer Technology and Development, 2009, 19(5): 217-219. DOI:10.3969/j.issn.1673-629X.2009.05.061 (  0) 0) |
| [2] |
ANFINSEN C B. Principles that govern the folding of protein chains[J]. Science, 1973, 181(4096): 223-230. DOI:10.1126/science.181.4096.223 (  0) 0) |
| [3] |
LAU K F, DILL K A. A lattice statistical mechanics model of the conformational and sequence space of proteins[J]. Macromolecules, 1989, 22(10): 3986-3997. DOI:10.1021/ma00200a030 (  0) 0) |
| [4] |
LAU K F, DILL K A. Theory for protein mutability and biogenesis[J]. Proceedings of the National Academy of Sciences, 1990, 87(2): 638-642. DOI:10.1073/pnas.87.2.638 (  0) 0) |
| [5] |
焉为家, 郭雨珍. 改进的粒子群算法求解蛋白质结构预测问题[J]. 计算机技术与发展, 2011, 21(12): 109-112. YAN Weijia, GUO Yuzhen. Modified particle swarm optimization algorithm for protein structure prediction problem[J]. Computer Technology and Development, 2011, 21(12): 109-112. DOI:10.3969/j.issn.1673-629X.2011.12.029 (  0) 0) |
| [6] |
陶凤英, 郭雨珍. 利用粒子群算法在菱形网格预测蛋白质结构[J]. 生物信息学, 2017, 15(2): 105-111. TAO Fengying, GUO Yuzhen. Predicting protein structure on rhombus lattice by particle swarm optimization[J]. Chinese Journal of Bioinformatics, 2017, 15(2): 105-111. DOI:10.3969/j.issn.1672-5565.20160702001 (  0) 0) |
| [7] |
汤达祺.基于BP神经网络的蛋白质结构并行分析[D].广州: 华南理工大学, 2016. TANG Daqi.The parallel analysis of protein structure based on back-propagation neural network[D].Guangzhou: South China University of Technology, 2016. (  0) 0) |
| [8] |
UNGER R, MOULT J. Genetic algorithms for protein folding simulations[J]. Journal of Molecular Biology, 1993, 231(1): 75-81. DOI:10.1006/jmbi.1993.1258 (  0) 0) |
| [9] |
李绍新, 张延娇. 改进的遗传算法在蛋白质结构预测中的应用[J]. 华南师范大学学报(自然科学版), 2009(1): 56-60. LI Shaoxin, ZHANG Yanjiao. The application of improved genetic algorithm for predicting protein structures[J]. Journal of South China Normal University (Natural Science Edition), 2009(1): 56-60. DOI:10.6054/j.jscnun.2009.02.014 (  0) 0) |
| [10] |
HOLLAND J H.Adaptation in natural and artificial systems[M].MIT Press, 1992, 6(2): 126-137.
(  0) 0) |
| [11] |
罗兵, 陈恒法, 邓虹. 基于遗传优化图像增强模糊算法[J]. 华南师范大学学报(自然科学版), 2007(1): 32-36. LUO Bing, CHEN Hengfa, DENG Hong. Image enhancement based on fuzzy logic optimized by CGA[J]. Journal of South China Normal University (Natural Science Edition), 2007(1): 32-36. DOI:10.3969/j.issn.1000-5463.2007.01.007 (  0) 0) |
| [12] |
NERIA E, FISCHER S, KARPLUS M. Simulation of activation free energies in molecular systems[J]. Journal of Chemical Physics, 1996, 105(5): 1902-1921. DOI:10.1063/1.472061 (  0) 0) |
 2019, Vol. 17
2019, Vol. 17


